传统风格建筑钢框架结构恢复力模型试验研究

薛建阳， 戚亮杰

(西安建筑科技大学 土木工程学院，西安 710055)

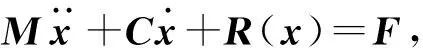
目前，针对钢结构框架或构件，较为通用的为三折线恢复力模型，李海锋等[5]对16根箱型钢柱进行了低周反复荷载加载试验，根据试验结果确定了偏心常轴压箱形钢柱的刚度退化和强度退化规则，提出大跨度空间结构箱形钢柱的恢复力模型；冉红东等[6]通过对K型高强组合钢偏心支撑的有限元分析，得到结构的三线型恢复力模型；石永久等[7]根据钢框架节点在低周反复荷载作用下足尺模型试验研究成果，建立了考虑组合效应的梁柱节点的恢复力模型；林倩等[8]在低周反复荷载试验的基础上，对钢桁架连梁模型的三折线恢复力模型进行了研究。上述研究结果均表明，钢结构三折线恢复力模型与试验结果吻合程度较高，适用性较好。

本文基于一榀1 ∶2比例传统风格建筑钢框架结构的低周反复加载试验结果，通过对其受力过程、破坏形态及滞回曲线的分析，提出适合该种结构类型的骨架曲线模型，同时，对试验数据进行多元线性回归分析，得到传统风格建筑钢框架结构在各受力阶段的刚度退化规律表达式，从而建立适用该结构类型的恢复力模型，对比该恢复力模型与试验结果，分析了建议的三折线恢复力模型的精确程度。

1 试验概况

1.1 试件设计

试件取自8度抗震设防烈度区某一殿堂式传统风格建筑的一榀单层两跨平面框架，尺寸大小按照宋《营造法式》古建筑“材份等级”制进行换算而得。其中，框架柱下部与框架梁分别为圆钢管和箱型截面形式。试件及其梁、柱构件尺寸如图1所示，T为驼峰，D和G分别代表斗与栱构件；试件连接采用全焊接的形式，整体框架模型如图2所示。钢材全部采用Q235B，钢材力学性能指标见表1。斗、栱构件尺寸及构造如图3所示。

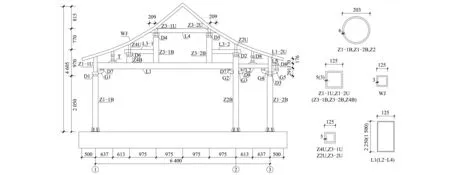
图1 试件模型Fig.1 Specimen model

图2 钢框架Fig.2 Steel frame

图3 斗栱尺寸Fig.3 Dimensions of Dou-Gong

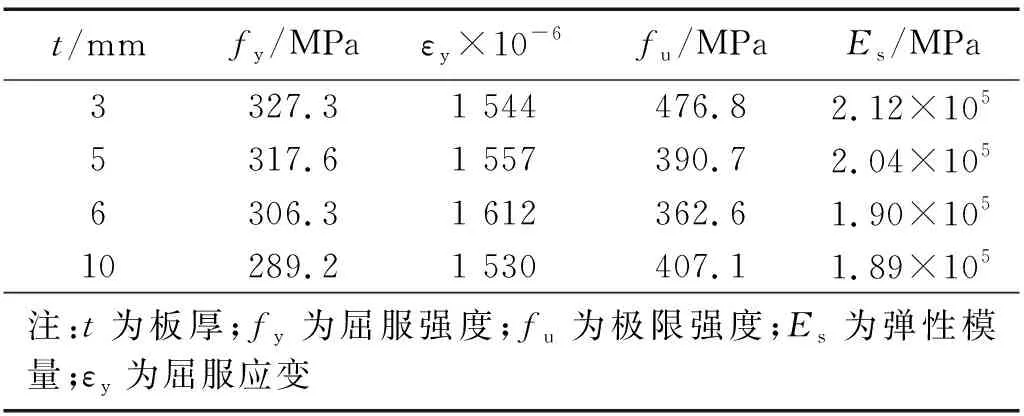
表1 钢材的材性Tab.1 Material properties of steel

斗栱及驼峰构件均由3 mm钢板制作而成，实物图见图4。

1.2 加载制度

参照《建筑抗震试验方法规程》(JGJ101-96)，加载时，采用悬挂荷载的方法，将屋顶面荷载等效施加在柱Z1-1、Z3-1、Z3-2、Z2、Z1-2的顶部，然后在大梁L1处通过电液伺服加载系统施加水平低周反复荷载，水平荷载采用力-位移混合控制加载的方式：试件屈服前，采用荷载控制并分级加载，每级荷载往复循环1次；屈服后采用位移控制，按屈服位移的倍数逐级增加，每级荷载反复循环3次。当试件不能继续承受反复荷载时，试验结束。试验在西安建筑科技大学结构工程与教育部重点实验室进行，加载装置和加载制度，如图5和图6所示。

图4 局部构造图Fig.4 Details of model

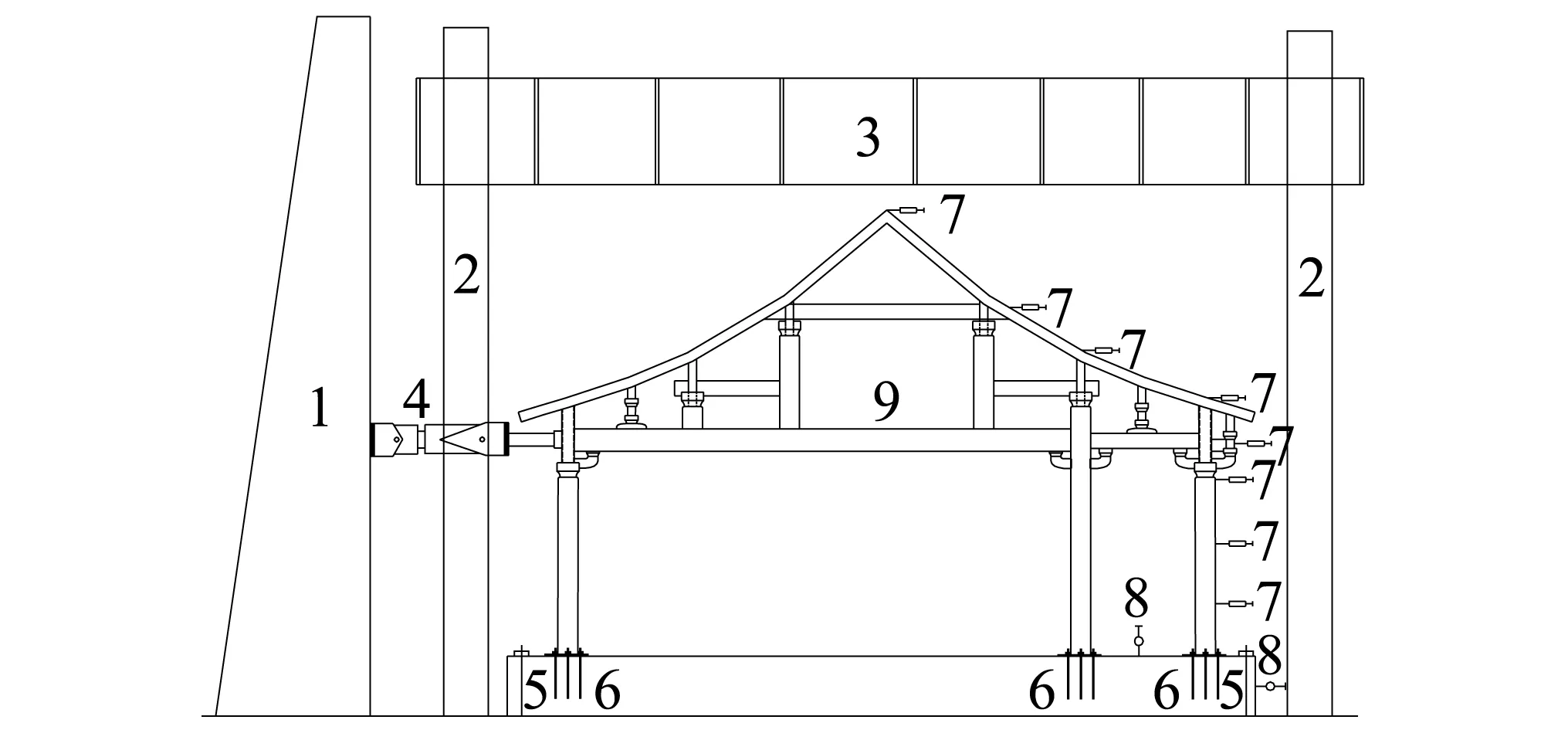
1.反力墙；2.反力钢架；3.反力梁；4.作动器；5.压梁；6.地脚螺栓；7.电子位移计；8.百分表；9.试件

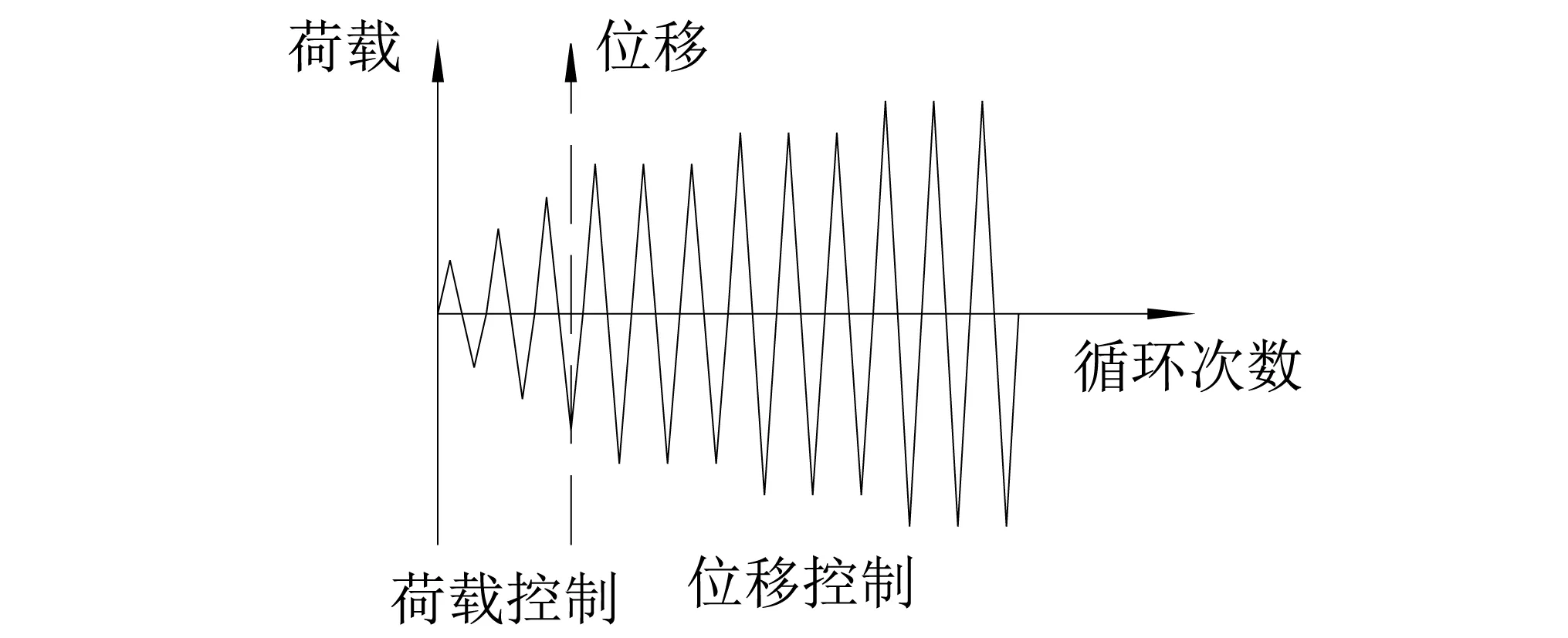
图6 加载制度Fig.6 Loading history

2 受力过程与破坏形态

在水平低周往复荷载作用下，传统风格建筑钢框架按其受力特征可以大体分为次要构件屈服、主要构件破坏及整体结构失效三个阶段，各个阶段特征表述如下。

次要构件屈服阶段：该阶段从开始加载至试件整体屈服。G2与D1最先达到屈服应变，之后D7与G2连接焊缝出现水平撕裂现象，G5腹板与下翼缘连接处开裂，其余构件均未屈服；整体框架水平位移较小，滞回曲线呈线性变化，结构没有明显的残余变形，试件处于弹性阶段。

主要构件破坏阶段：是从试件屈服至结构达到峰值荷载的阶段。G3上翼缘与G2腹板内凹，L1右端发生外凸变形；随着荷载的增大，梁端发生破坏现象，L1右端母材拉断且裂缝几乎贯通，L2左端焊缝撕裂，Z2与L2完全断开，钢框架体系受力发生变化，Z1-1、Z1-2柱脚接近屈服，结构承载力降低明显，钢框架完全进入塑性阶段。

整体结构失效阶段：钢框架结构承载能力开始下降，框架柱的柱脚全部屈服，整体变形非常明显，在试验结束时，Z1-2与L2交接处节点核心区刚好达到屈服状态，其余两个节点核心区尚未屈服；从整体上来看，结构破坏较为显著，刚度退化严重，卸载后试件的最大残余变形达到60.76 mm。

图7为钢框架中典型构件的破坏形态，从结构的受力过程和破坏形态可以看出，传统风格建筑钢框架结构的屈服顺序由先到后为“斗栱-梁端-柱底-节点核心区”，满足我国规范要求的“强柱弱梁，强节点弱构件”的抗震设防原则，抗震性能较好。

图7 典型破坏形态Fig.7 Typical failure modes

3 特征曲线分析

3.1 滞回曲线

结构的滞回曲线综合反映了结构的抗震性能，传统风格建筑钢框架结构在低周往复水平荷载下得到的荷载-位移滞回曲线如图8所示，图中P，Δ分别表示试件水平荷载和水平位移。在试验初期，钢框架处于弹性工作状态，滞回曲线基本呈线性关系变化，卸载时无残余变形；随着加载的继续，局部结构破坏较为明显，结构次要构件如斗、栱间发生水平错动，对角线方向发生剪切破坏，滞回曲线出现一定的捏缩现象；在峰值荷载点附近，结构梁端裂缝贯通，梁-柱之间空隙加大，承载力和刚度退化较为明显，滞回曲线的捏缩现象十分显著，由反S形逐渐转变为Z形变化。

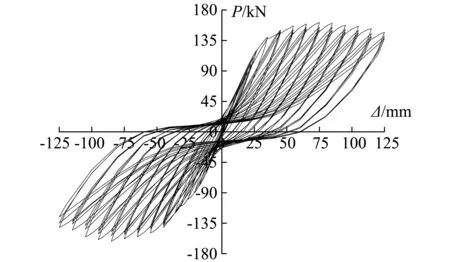
图8 滞回曲线Fig.8 Hysteretic loops of specimen

3.2 骨架曲线

骨架曲线可以综合反映结构的延性、承载能力、刚度退化等抗震评估指标[9]。本试验得到的传统风格建筑钢框架结构的骨架曲线，如图9所示。

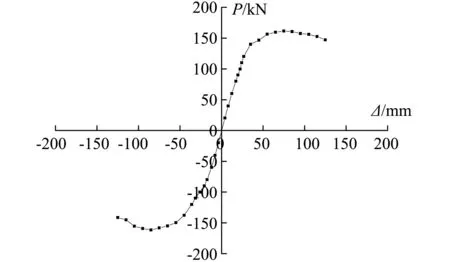
图9 骨架曲线Fig.9 Skeleton curve

从图9所示试验结果可以看出，试件屈服后经历了较长的强化阶段，承载力较高，峰值荷载达到161.67 kN，随后，荷载逐渐降低但下降幅度较为平缓，整体框架并没有发生明显的承载力陡降现象，说明结构加载后期刚度退化较慢且具有良好的变形能力。

4 恢复力模型

4.1 骨架曲线建议模型

当传统风格建筑钢框架结构承受的重力荷载发生变化时，结构的承载力及位移变形情况也将发生变化，为了将恢复力模型的研究成果推广使用统一的公式图形表示，因此将本试验所得的骨架曲线进行无量纲化，即分别采用P/ |Pm|、Δ/ |Δm| 为纵坐标与横坐标，其中Pm、Δm分别表示试验测得的结构承受的最大荷载与其相对应的位移。

分析试验得到的骨架曲线可以发现，传统风格建筑钢框架模型加载时呈现出明显的3个阶段，因此我们将无量纲化的骨架曲线简化为三折线模型，如图10所示，其中，控制点A、D分别代表结构在正负向荷载作用下的屈服点，由能量等值法[10]确定；控制点B、E分别代表正负向加载时结构的承载力峰值点；控制点C、F表示结构的加载失效点，此时钢框架结构已不能继续承受反复荷载。各特征点数值示于表2当中，对三折线模型的各加载阶段数据进行拟合并得到其回归方程及斜率，示于表3中。

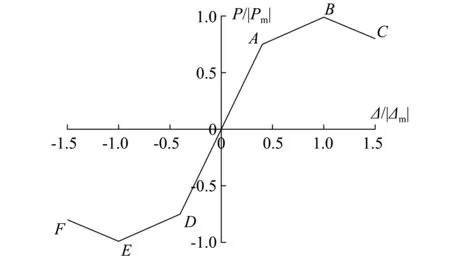
图10 骨架曲线建议模型Fig.10 Model of skeleton curve

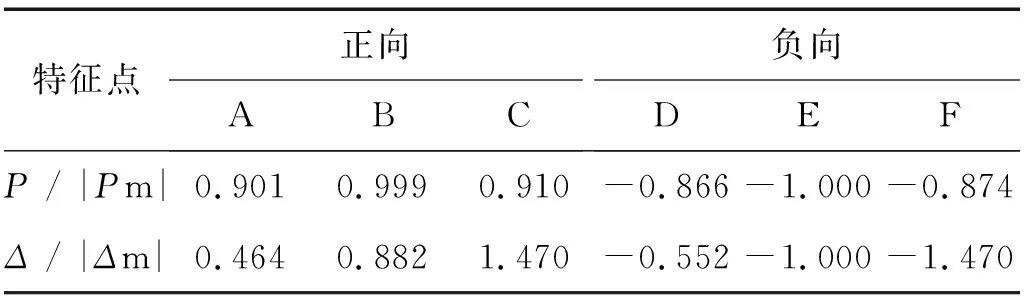
表2 控制特征点Tab.2 Control point

表3 骨架曲线模型回归方程Tab.3 Equations of skeleton curve model

将试验实测数据点与骨架曲线模型同时绘制于图11当中，可以看出，本文所提出的传统风格建筑钢框架结构三折线建议模型与试验结果吻合较好，说明三折线模型可以较好的反应该种结构在水平荷载作用下荷载与位移的变化情况。

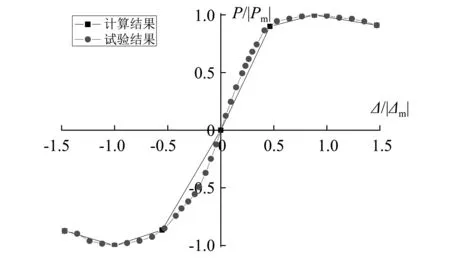
图11 骨架曲线计算模型与试验结果对比Fig.11 Comparison between calculated and experimental results

4.2 刚度退化规律

通过对试验数据的统计回归分析，可得到传统风格建筑钢框架结构的刚度退化规律。本文中K1、K2、K3、K4分别表示滞回环的正向卸载刚度、负向加载刚度、负向卸载刚度及正向加载刚度。在加载初始阶段，对前期试验数据进行线性拟合得到正向及负向初始加载刚度K0+和K0-。

4.3.1 正向卸载刚度K1

将试验所得的正向卸载点1与荷载降为零的数据点连接，得到的线段为正向卸载线，其斜率即为正向卸载刚度K1。通过回归分析即可得到K1/K0+与Δ1/Δm+的关系曲线，如图12(a)所示；正向卸载刚度方程如下式所示：

K1/K0+=
0.356 6+1.064 4·exp(-1.182 1Δ1/Δm+)

(1)

式中：Δ1为正向卸载点1对应的位移，Δm+为正向加载时的峰值位移。

4.3.2 负向加载刚度K2

将试验所得的正向荷载降为零的点2与加载至负向峰值荷载点之间的数据点连接，得到的线段为负向加载线，拟合得到其斜率即为K2。通过回归分析即可得到K2/K0-与Δ2/Δm+的关系曲线，如图12(b)所示；负向加载刚度方程如下式所示：

K2/K0-=
0.0554 +0.5082·exp( -2.265 5Δ2/Δm+)

(2)

式中：Δ2为负向加载点2对应的位移。

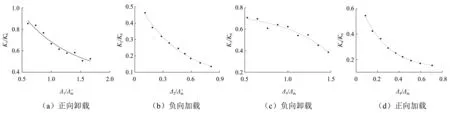
图12 各阶段刚度退化曲线Fig.12 Stiffness degradation curves

4.3.3 负向卸载刚度K3

将试验所得的负向卸载点3与荷载卸为零的数据点连接，得到的线段为负向卸载线，拟合得到其斜率即为负向卸载刚度K3。通过回归分析即可得到K3/K0-与Δ3/Δm-的关系曲线，如图12(c)所示；负向卸载刚度K3退化曲线方程如下式所示：

K3/K0-=
0.765 7 - 0.026 7·exp(1.802 1Δ3/Δm-)

(3)

式中：Δ3为负向卸载时点3对应的位移；Δm-为负向加载时的峰值位移。

4.3.4 正向加载刚度K4

将同一加载循环下负向荷载卸为零的数据点4与正向峰值荷载点连接，得到的线段为正向加载线，拟合得到其斜率即为K4。通过回归分析即可得到K4/K0+与Δ4/Δm-的关系曲线，如图12(d)所示；正向加载刚度K4退化曲线方程表达式为：

K4/K0+=
0.122 8 - 0.603 6·exp( -4.2355Δ4/Δm-)

(4)

式中：Δ4为负向卸载后的残余位移。

4.3 恢复力模型的确定

根据低周反复试验得到的传统风格建筑钢框架结构骨架曲线模型、滞回曲线变化规律及各阶段刚度退化规律，最终建立适用于该种结构类型的三折线恢复力模型，其滞回规则如图13所示。该模型可以反映出传统风格建筑钢框架结构次要构件屈服阶段、主要构件破坏阶段以及整体结构失效阶段的受力特征，同时可以将结构的刚度随加载进程深入而不断退化的规律反映出来[11]。

传统风格建筑钢框架结构三折线恢复力模型具体滞回规则可描述如下：

图13 恢复力模型滞回规则Fig.13 Hysteretic rule of restoring force model

(1)在加载过程中，当结构未屈服时，处于弹性状态，正、负向加载分别沿着直线O-A和O-D段变化，卸载时仍沿着骨架曲线弹性阶段进行，正、负向卸载刚度分别与初始加载刚度K0+、K0-一致。

(2)当结构达到屈服强度但未达到极限强度时，由于框架刚度退化，在点1处卸载后路径将沿1-2段进行，1-2线段为该圈滞回环的正向卸载线。当从点2开始负向加载时，若结构负向尚未屈服，则加载路线指向负向屈服点D，即负向加载线为2-D；若结构负向已经屈服，则加载路径指向上级加载时的最大位移点3，此时负向加载线为2-3。在反向D-E段卸载时，卸载路线由点3按照负向卸载刚度K3指向点4，3-4线段即为负向卸载线。继续正向加载时，若所加荷载大于结构极限承载能力，则加载路径为4-1-5，4-1线段斜率即为正向加载刚度K4。

(3)当加载至点5再卸载时，卸载路线为5-6。随后负向加载时，若负向仍未达到峰值荷载，则加载路线指向峰值点E，即按照6-E-F的路线进行；若负向已经达到峰值荷载，则加载路线指向上级加载的最大位移点7，沿着6-7-F的路线进行。若在负向E-F段卸载并正向加载时，将按照7-8-5-C的路线继续进行。

4.4 滞回曲线计算结果与试验结果对比

为了解传统风格建筑钢框架结构的抗震性能，课题组对该种结构的一榀框架进行了低周反复加载试验，将试验得到的滞回曲线与三折线恢复力模型计算结果进行对比，示于图14当中，从图中可以看出，本文确定的三折线恢复力模型曲线与试验滞回曲线趋势相同，吻合程度较高，说表明该恢复力模型能够较好地反映传统风格建筑钢框架结构的滞回性能，为该种结构在地震作用下的弹塑性动力分析奠定了基础。

5 结 论

(1)传统风格建筑钢框架结构在低周往复荷载作用下，按其受力特征分为次要构件屈服、主要构件破坏及整体结构失效三个阶段。屈服顺序由先到后为“斗栱-梁端-柱底-节点核心区”，满足我国规范要求的“强柱弱梁，强节点弱构件”的抗震设防原则，抗震性能较好。

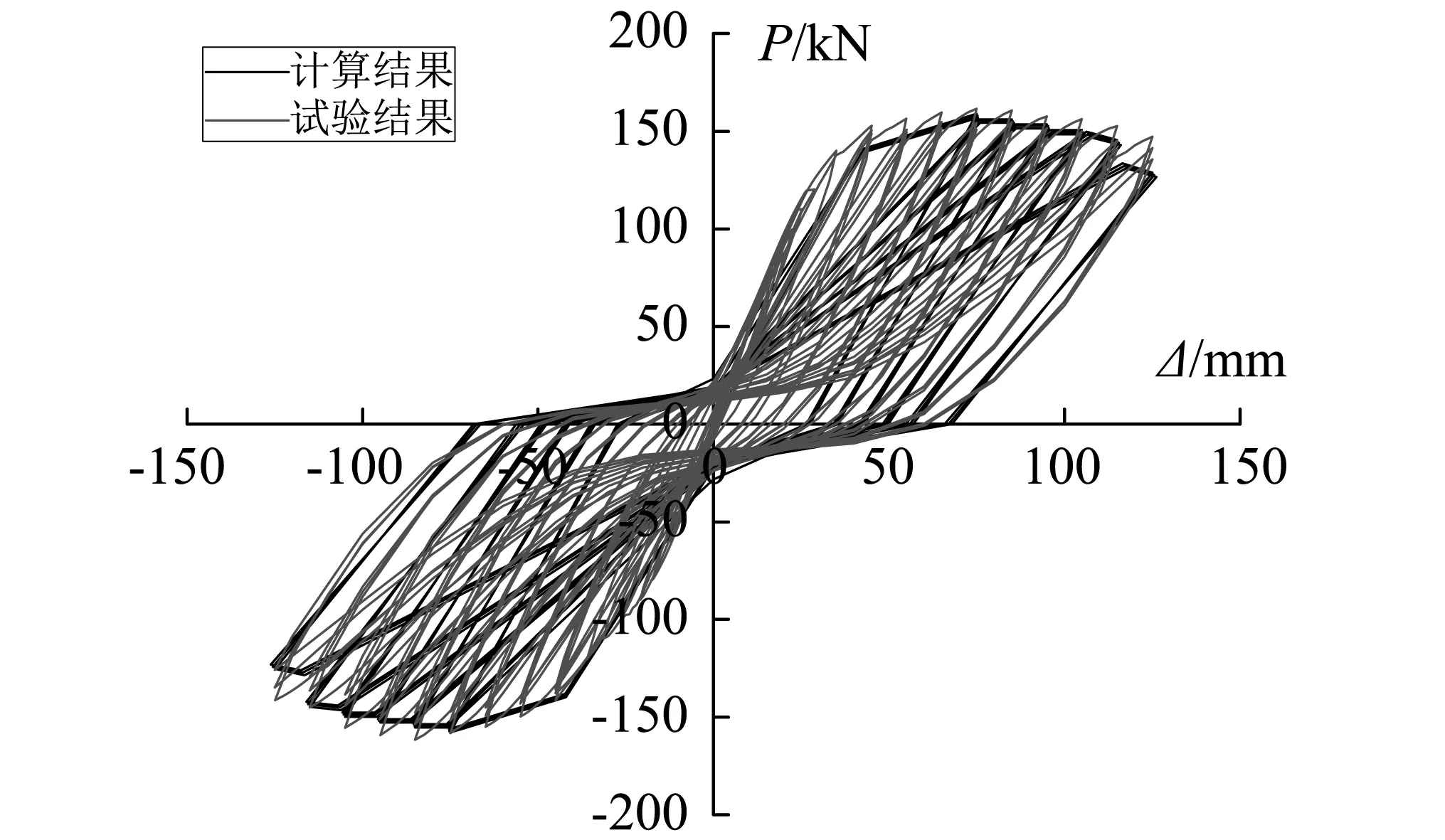
图14 恢复力曲线模型与试验结果对比Fig.14 Comparison between restoring force model and experimental results

(2)当加载至峰值荷载点时，结构梁端裂缝贯通，梁-柱之间空隙加大，承载力和刚度退化较为明显，结构的滞回曲线表现出一定的捏缩现象。峰值荷载过后，荷载下降较为平缓，整体框架并没有发生明显的承载力陡降现象，说明传统风格建筑钢框架结构刚度退化较慢且具有良好的变形能力。

(3)基于试验结果，建立了无量纲化的三折线骨架曲线模型，运用指数函数拟合出加载各阶段的刚度退化方程，结合其滞回特性和刚度退化规律，最终建立适用传统风格建筑钢框架结构的三折线恢复力模型；提出的骨架曲线模型及恢复力模型与试验结果吻合程度均较高，可为传统风格建筑钢框架结构的弹塑性动力分析提供理论参考。