水利水电工程施工多元协同优化模型研究

赵尹利，李艳玲，张 瀚，安慧琳

(1.四川大学水利水电学院，成都 610065； 2.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

水利水电工程地形地质条件复杂、建设周期长、涉及因素广泛，其施工方案优化必须综合考虑施工安全、质量、进度、投资、环境之间复杂的制约关系，并对其科学合理的管控，方能保证工程项目建设的科学性和高效性[1]。目前，国内外对五大目标的单项管控理论研究已较成熟，针对每个目标，均提出了许多科学的管理和评价方法[2,3]。近年来，众多研究者开始针对工程施工进度、质量、成本三大目标，建立起均衡优化模型，并使用遗传算法[4]、蚂蚁算法[5]和微粒群算法[6]等多种算法进行优化求解，但是，此类模型很少定量考虑到施工安全和环境的影响。随着社会对工程安全和环境保护意识的不断深化，基于进度、质量和成本的传统综合均衡优化模型已不能满足现代施工管理的要求。因此，本文针对施工安全、质量、进度、投资和环境五大目标，考虑其对立统一关系，选定主控因子，构建主控因子与多目标因子的多元关系函数以定量分析主控因子变化对其他目标因子的影响程度，再利用方案优选步骤实现施工方案的多因子协同优化。此模型能够针对各个工程的不同特点定制出一套科学的优化方案，也能为其他工程领域的施工方案优化提供一定的参考价值。

1 模型构建

基于主控因子的施工多元协同优化模型的核心是建立施工安全、质量、进度、投资、环境等目标因子间的多元关系函数，实现施工方案的多因子协同优化。

1.1 多元关系函数构建

多元关系函数的构建应首先结合工程实际情况，选择一个目标作为主控因子p，再分别构建该主控因子和其他协调因子的“目标因子-主控因子”关系函数，从而定量获取主控因子变化对其他因子的影响程度。本文以施工进度为主控因子，构建“其他因子-进度”关系模型。

(1)质量-进度关系模型。在允许工期范围内，适当压缩工期对工程质量影响较小，但一旦超过极限工期，其质量水平则会迅速下降，因此可采用自然对数函数表达质量-工期关系[7]，如图1，从而构建质量-进度关系模型如式(1)。

(1)

式中：ai=(e-eQi)/(tni-tsi)；bi=(eQi·tni-e·tsi)/(tni-tsi)；r为项目包含的工作数；tni为工作i的正常工作时间；ti为工作i的实际工作时间；tsi为工作i的极限工作时间；φi为工作i质量权重系数；Qi为工作i实际状态下的质量水平。

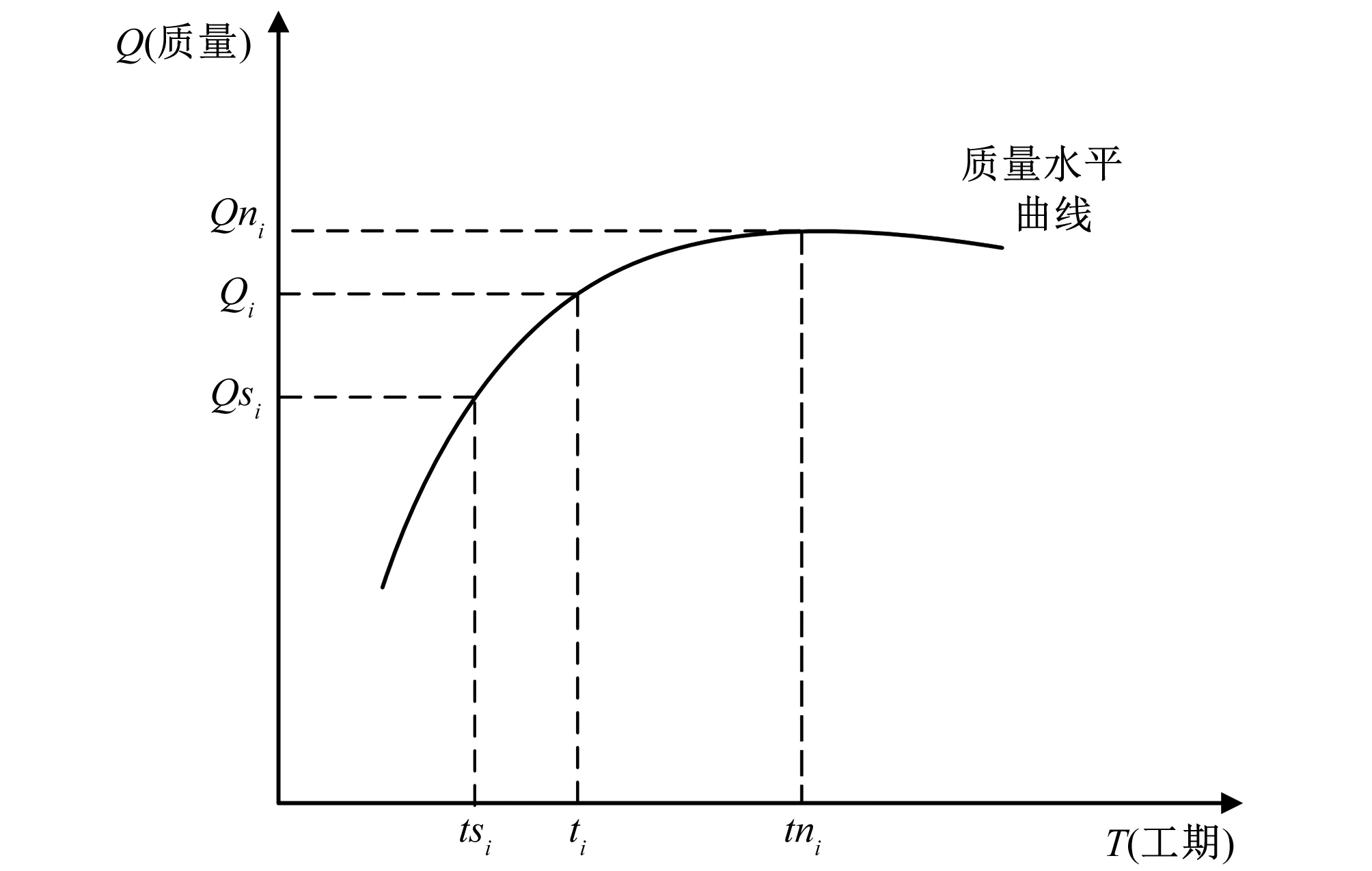
图1 质量水平与工期关系曲线Fig.1 Relationship diagram of quality level and progress

(2)投资-进度关系模型。工程项目建设的投资费用可分为直接费用、间接费用和工期奖罚费用[8]。直接费用包括直接工程费和措施费，与工期呈二次曲线特性；间接费用包含企业管理费和规费，和工期奖惩费用会随着工期的缩短成比例的下降，因此，直接和间接费用之和与时间呈开口向上的抛物线关系，抛物线顶点所对应的时间，即工作i的实际工作时间，产生的总投资最优。投资-进度关系曲线如图2，关系模型如下：

(2)

式中：r为项目包含的工作数；αi为工作i的工作时间压缩时的费用增加变化率，αi≌(Csi-Cni)/(tni-tsi)；tni为工作i的正常工作时间；ti为工作i的实际工作时间；tsi为工作i的极限工作时间；Cni为工作i在正常工作时间下的直接费用；Csi为工作i在极限工作时间下的直接费用；βi为与工期有关的间接费系数(每单位时间的间接费用)；β2为计算工期超过或小于合同工期的奖罚系数；T为实际工期；Th为合同工期。

图2 投资费用与工期关系示意图Fig.2 Relationship diagram of cost and progress

(3)安全-进度和环境-进度关系模型。安全和环境的量化指标可采用安全可靠度和环境保持度。环境-进度和安全-进度具有相同的变化关系，即工期正常情况下，适当缩短工期，工程的安全可靠度和环境保持度均下降较缓，若继续压缩工期超过了极限工作时间，安全可靠度和环境保持度均会直线下降。因此，本文利用线性和二次函数分段模拟其相关关系，得到安全-进度和环境-安全曲线如图3，关系模式如式(3)。

(3)

式中：r为项目包含的工作数；tni为工作i的正常工作时间；ti为工作i的实际工作时间；tsi为工作i的极限工作时间；wi为工作i安全(环境)的重要程度；Sni为工作i在正常工作时间下的安全可靠度(环境保持度)；Si为工作i实际状态下的安全可靠度(环境保持度)；Ssi为工作i极限状态下的安全可靠度(环境保持度)。

图3 安全可靠度(环境保持度)与工期关系示意图Fig.3 Relationship diagram of safety reliability (Environmental retention) and progress

1.2 多因子协同优化方法和步骤

(1)建立多目标方案集。在满足相关规定、资源可供以及不改变工程特性情况下，改变主控因子量值，得到一系列的计划方案，再由上述关系模型，得到每个计划方案所对应的目标因子的量值，构建出多目标方案集。例如，当以进度主控时，首先，将工期由正常工期压缩至极限工期，得到一系列施工工期；再根据施工网络计划图，利用“进度-目标因子”4个关系模型[如式(1)～式(3)]，计算出各个方案施工投资费用、质量水平、安全可靠度和环境保持度，构建多目标方案集为：

(4)

(2)建立规范化赋权矩阵。首先用梯形隶属度函数[9]将式(4)转化为规范化矩阵，对越大越优的目标，利用升半梯形；越小越优的目标，利用降半梯形；中性目标P0，利用中间型梯形。再对矩阵进行赋权，可采用主观赋权和客观赋权法，其中，客观赋权主要包括熵权法、标准离差法和CRITIC[10]等，得到加权的标准化矩阵X，xij计算如下式：

xij=wizij,i=1,2,3,…,m;j=1,2,3,…,n

(5)

(3)计算各方案灰色关联系数。首先确定各个目标所对应的最优解X+=[x+1,x+2,…,x+m]T和最劣解X-=[x-1,x-2,…,x-m]T，其中x+i和x-i元素分别为：

x+i=max{xi1,xi2,…,xin},x-i=min{xi1,xi2,…,xin}

(6)

再计算各方案i分别与最优解和最劣解关于指标i的灰色关联系数：

(8)

式中：ε为分辨率，0<ε<1，一般取ε=0.5。

(5)得出优化方案，即依据灰色相对贴近度对方案进行优劣排序。计算各方案与最优、最劣解的灰色关联相对贴近度μj,再从大到小对相对贴近度进行排序，相对贴近度最大的方案即为最优方案，方案j的相对贴近度μj由下式得到：

(9)

2 工程实例

某大坝工程施工进度网络计划见图4，2016年9月至2018年1月之间是该工程施工高峰期。考虑工程特点和施工要求，选择以进度为主控目标，根据上文所构建的进度主控关系模型，进行参数的设定与生成，得到各项目相关参数如表1。

图4 某大坝工程施工进度网络计划图Fig.4 network plan of a dam project

表1 建设项目网络计划相关参数Tab.1 Related parameters of construction project network plan

综合考虑施工度汛、资源配置等因素，对正常工期进行压缩，确定出7种工期可行方案。采用式(1)～式(3)的关系函数，分别计算七种可行方案的工期、质量水平、投资、安全可靠度和环境保持度见表2。

表2 各方案工期、质量水平、投资、安全可靠度和环境保持度量值Tab.2 Project duration, quality level, investment, safety and reliability and environmental maintenance

依据上文构建的进度主控的多元管控模型，多目标矩阵P为：

把目标特征值矩阵转换为规范化矩阵R：

采用标准离差法对工期、质量、投资、安全和环境五个目标进行赋权，再参照本建设项目对五大控制目标的偏好权重，对此权重向量进行修正，其修正后向量为：

C=(0.25，0.25，0.25，0.15，0.10)

根据式(6)可以确定各个目标所对应的最优解X+=(0.25，0.25，0.25，0.15，0.10)T,X-=(0，0，0，0，0)T。

计算各方案与最优解X+的灰色关联度r+为：r+=(2.676 8，2.625 7，2.829 5，3.276 9，2.738 1，2.908 3，1.929 7)，各方案与最劣解X-的灰色关联度r-为：r-=(3.343 4，2.520 0，2.462 8，2.547 9，2.907 7，3.441 7，4.430 4)。

计算各方案与最优、最劣解的灰色关联相对贴近度μj：

μj=(0.444 6，0.510 3，0.534 6，0.562 6，

0.485 0，0.401 4，0.303 4)

最后根据其相对贴进度的大小对本建设项目的7个可行的方案进行排序，其排序的结果为：

方案4>方案3>方案2>方案5>方案1>方案6>方案7

相对贴近度最大的方案即为最优方案，因此本建设工程此时间段内进行目标控制的最优方案为方案4，其工期即为553 d，费用为50 878.9 万元，质量水平为0.965 2，安全可靠度为0.985 8，环境保持程度为0.973 4。

3 结 论

本文提出的基于主控因子的施工多元协同优化模型能定量考虑该五大施工目标的综合影响，实现施工方案的多因子协同优化，可大幅提升决策结论的合理性和客观性。该模型运用于实际工程时，可根据每个工程不同的特点和需求选取合适的主控因子，并建立不同主控因子与其他协控因子的关系函数，为施工智能管控系统的研发奠定一定的理论基础。

□