结合RVA法建立天然径流量还原计算的BP神经网络模型
刘 强,冯忠伦,刘红利,王 维,林洪孝,王 刚
(1.山东农业大学 水利土木工程学院,山东 泰安 271018;2.河海大学,南京 210000)
0 引 言
20世纪50年代以来,随着社会经济发展带来耗水量的增加和水利工程的修建,人类活动对流域的干扰性越来越大,比如水利工程的拦蓄、分洪对河川径流的调节和改变,造成了河流的水文情势已不能保持原来的情况,许多水文站断面实测径流量,已经不能反映本流域真实天然来水量[1]。这种情况对水资源评价和水资源工程的合理规划与利用十分不利。因此,要想得到准确的天然来水量就必须对河川径流量进行还原计算,还原到没有水利工程影响下的情况,进而对开展水资源评价项目大有裨益。
当前,国内外水量还原计算方法的研究主要是基于水量平衡的逐项还原法,这种方法突出优点就是准确性较高,一项一项的还原计算,但与此同时资料要求较高,各行各业历年资料要求较全,而现状是在一些偏僻缺少测站的流域,有可能不能满足资料齐全的要求,因而水量还原计算举步维艰,难以开展。随着科学技术的发展,计算机算法的推广,可以利用BP神经网络非线性映射的优点应用到像水量还原计算的问题上。因此,本文首先运用RVA法[2]建立RVA模型对大沽夹河流域水文情势进行分析计算,在此基础上建立BP神经网络[3]天然径流量还原计算模型,并与传统的逐项还原法进行对比,讨论方法的适用性。
1 研究区概况
大沽夹河流域地处胶东半岛的山东烟台市,由东西两大支流—东支外夹河,西支清洋河汇合而成,总的河长75 km,总流域面积2 296 km2,是烟台市区最为重要的供水来源。如图1给出了本次研究区水利工程的分布情况,其中中型水库桃园水库1座,小(Ⅰ)型水库16座,小(Ⅱ)型水库61座,控制流域面积总计146 km2,总的兴利库容0.33 亿m3,建有八座拦河闸坝,拦蓄了1 200 万m3水量。
此次应用的资料经过1982年省水利厅《山东省调查资料》及1991年烟台市水利局刊布的《烟台水利志》等资料,搜集到历史资料可靠程度较强,可以用于研究。
2 研究方法
2.1 RVA评估方法及计算步骤
变化范围法(Range of Variability Approach)[4,5]的提出,建立在日流量数据为基础,以水利工程建设前的自然状态为基准,统计了33个IHA指标受人类活动[6]干扰前后的变化情况,定量计算出33个水文指标的水文改变度。具体计算步骤如下:
(1)将描绘河流水文情势的33个水文指标按分为3组[7],分别为月平均流量、年极端流量与其他反应水文情势的参数。
(2)计算各参数的平均值和标准差,确定33个流量管理目标。通常该目标的范围为平均值 标准差或是以频率为75%~25%所对应的流量为可接受的环境流量范围,即流量高低阈值,也称为上下限,统计水利工程建设前后流量落在上下限内的年份。
(3)按公式(1)、(2)计算河流在受人类活动影响后的各参数的水文变化度,量化反映水利工程的建设对流量的影响[8]。用下式进行评估[9]:
(1)
Ne=rNr
(2)
式中:Di为第i个IHA参数的水文改变度,用以衡量该参数水利工程建设后的变化剧烈程度;No与Ne分别为受到干扰后及预期收到干扰后的观测年数中的IHA指标落入RVA目标内的年数;r为干扰前的IHA指标落入RVA目标内的比率;Nr为受干扰后的流量时间序列总长度。
2.2 水文改变度[10]
从2.2节RVA评估方法中由公式1、2计算得到的水文变化度是用来量化评估河川水流特性受水利工程影响,平均划分了3个等级,即零改变或低度改变(0%~32%)、中度改变(33%~66%)和高度改变(67%~100%),并认为水文变化度低于33%均为可接受,水文改变度的提出较为直观地反映了本流域水文情势改变情况,提供了量化数据,并分了三个不同的等级,合理性较高。
2.3 BP神经网络模型
BP神经网络通常是指基于误差反向传播算法算法的多层前向神经网络,模型包括输入层、中间层和输出层,如图1所示。由于权值的调整采用反向传播的学习算法,通过误差的反向传播不断调整内部连接的权值和阈值[11,12],达到减小误差的目的,最终得到最优取值。

图1 BP神经网络运行示意图Fig.1 Operation diagram of BP neural network
公式(3)表示了网络的权值及阈值调整过程公式。
f(x)=[1+exp(-x+θ)]-1
(3)
公式(4)~(5)表示了隐层输入项与输出项:
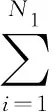
(4)
Ojp=f(netjp,θJ)=[1+exp(-netjp+θj)]-1
(5)
式中:Wji表示输入层第i节点与隐含层第j节点间的连接权系数;θJ为隐含层的阈值。对于输出层来说,输入netkp和输出Okp如公式(6)和公式(7)所示:

(6)
Okp=f(netkp,θk)=[1+exp(-netkp+θk)]-1
(7)
公式(8)给出了误差Ep,代表样本的期望输出值情况:
(8)
3 实 例
3.1 基于RVA法的水文情势评估模型
大沽夹河流域共东西两支,由于西支的门楼水库在1960年建库,建库前数据较少(仅1950-1960十年建库前资料),数据年限较短,对RVA模型评估结果造成误差较大,因此本次研究选取大沽夹河流域的东支外夹河流域进行评估分析。根据外夹河流域水利工程建设情况,以及1953-2016年降雨径流资料,将外夹河流域分为1953-1980年和1981-2016年两个时段分别作为本流域受人类活动修建水利工程干扰前和干扰后的情况,对比评估人类修建水利工程对河流径流过程的影响。
3.1.1 月流量变化分析
由表1可以看出,月平径流在水利工程建设后变化显著。1-4月、10-12月7个月的径流发生中度改变,其余月份发生低度改变。其中1月份径流均值改变度最大(D=0.54),11月份次之(D=0.49)。 在均值方面,1-5月的流量均值在水利工程建设后均比建设前有所增加,6-10月份的流量在建设后有所减少,呈现了最小流量值整体呈上升趋势,最大流量值整体呈下降趋势。具体表现为,1-4月份流量均值分别从24.3、26.7、34.3、38.7 m3/s增加到34.5、32.8、38.4、51.9 m3/s;6-10月份流量均值分别从498.0、727.1、793.3、540.1 m3/s增加到484.2、584.2、633.8、399.5 m3/s;在最小值方面,水利工程建设前有0流量,建设后非汛期则没有了0流量的现象,最大值由建库前的3 229.3 m3/s降低到2 975.8 m3/s。结果表明水利工程的建设运行削减了洪水期流量,增加了枯水期径流,具有蓄丰补枯的作用。对比如图2所示。

表1 水利工程建设前后福山站水文指标的改变程度Tab.1 Changing degrees of hydrological indexes in Fushan station before and after water conservancy project construction

图2 水利工程建设前后月平均流量对比图Fig.2 The comparison diagram of mean monthly flow before and after water conservancy project construction
3.1.2 年极端流量变化分析
从表2及图3~图7可以看出,年极限流量指标均发生不同程度改变,可见水利工程的建设对河流的年极端流量的影响。具体来讲,年最大流量明显变小,且短历时最大流量值比较长历时最大流量值变化更为显著,其中以最大1日流量减少最为明显,由建库前的2 410 m3/s将为建库后1 456 m3/s,减少近1 000 m3/s;而年最小流量明显增大,且长历时最小流量变化更为显著,其中最小90日流量变化最大,较建库前的45.5 m3/s增加到建库后的61.3 m3/s。可见水库通过蓄丰补枯,消减洪峰,显著地改变了流量的极值,使极大值减少,极小值增大。
3.1.3 年极限流量发生时间
水利工程建设前后年极端流量发生时间变化不大,极大值出现时间大部分仍集中在6-9月汛期,但期内分布不均,该指标只发生低度改变,而极小值出现时间波动范围广,与建设前差异较为突出,大多发生在枯水期(12-2月),偶尔发生在汛期前的5、6月份,因此,年极限最小流量发生时间改变度较大。
3.1.4 高、低流量出现的频率及延时
在变化范围法(RVA)中,受人类活动影响前,日流量发生几率大于75%的属于高流量,发生几率小于25%的属于低流量。建设后每年发生高流量次数减少,低流量出现次数增多,与此同时,高流量平均延时增加,低流量平均延时减少(如表3);高低流量延时的变化主要是由于水利工程对洪水的调节,在丰水年消减洪峰而延长洪峰历时,再枯水年流量较大时储存部分径流保证枯水期满足发电、灌溉等需求。

表2 福山站年均流量极值的RVA分析Tab.2 Statistical analysis of the annual extreme runoff at the Fushan station

图3 福山站历年最大最小1 d平均流量Fig.3 1 d maxmum and minmum daily average flows in Fushan station

图4 福山站历年最大最小7 d平均流量Fig.4 7 d maxmum and minimum daily average flows in Fushan station
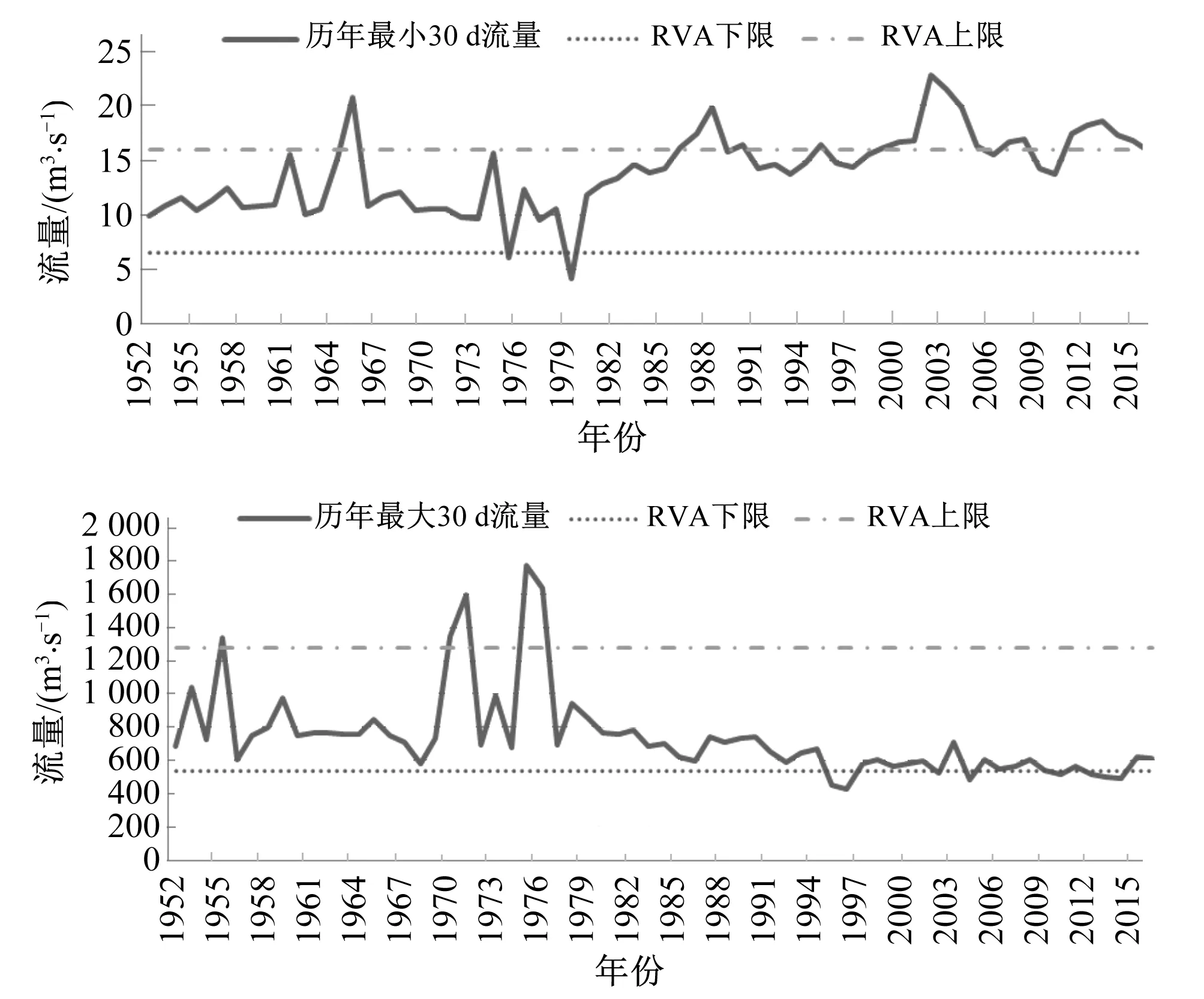
图5 福山站历年最大最小30 d平均流量Fig.5 30 d maxmum and minimum daily average flows in Fushan station

图6 福山站历年最大最小90 d平均流量Fig.6 30 d maxmum and minimum daily average flows in Fushan station
3.1.5 流量变化改变率及频率
修建水库等水利工程后,径流在经过调节后,流量的平均增加率和减少率都呈不同程度减少,同样是由于水利工程的削峰补枯作用,延缓了洪水的涨落速度;在流量的逆转次数方面,变化度为0.36,属于中度改变,具体指标变化特征统计见表3。
3.1.6 RVA法模型的应用总结
本文引入了变异范围法(RVA),建立了评估流域水情的RVA模型,提出了水利工程建设前后水文条件变化的分析方法,并以大沽夹河流域福山站所在的外夹河流域为例,进行了实例研究。结果表明,汛期流量有所减少,非汛期流量有所增加,年极端最大最小流量中也发生了改变,其他水文特征值均变化显著,所以可以评估出水库等水利工程的修建对福山站水文条件有明显的改变,在一定程度上破坏了原有的天然状态。但河流水资源的合理开发与利用离不开天然径流量的数据,因此,在RVA模型研究的基础上引入了BP神经网络模型,把两种模型进行结合对大沽夹河流域天然径流量进行还原计算,得到有效的天然径流量数据投入水资源工作中。

表3 福山站多年径流量的变化特征统计分析表Tab.3 Statistical analysis of the variation features of the annual runoff at the Fushan station
3.2 BP神经网络天然径流量还原计算模型
3.2.1 BP模型的构建
以降雨量和汛期径流量为输入,天然径流量为输出构建天然径流量计算的BP神经网路模型。其输入层节点为2个(影响因子为降雨量与实测径流量),隐含层节点神经元为10个(隐层节点数试算法求出),输出层节点为1个(天然径流量)。权值训练模型使用的是L-M优化算法的trainlm函数,选取purelin函数作为输出层传递函数,迭代次数每次100次,上限设定10 000次,达到训练目标误差0.001时训练结束;使用premnmx函数把原始数据归一化处理在[-1,1]之间,具体如表4所示。
3.2.2 BP网络模型训练与仿真
选取福山站45年(1956-2005)的系列资料的年均降雨量P和年均实测径流量R实作为已知样本,用其前35年的样本对网络进行训练,用后十五年的样本对网络进行检验与模拟。模型在运行830次的时候达到所需误差0.001,训练完备,仿真的实测与模拟对比值如图7所示。

图7 模型的仿真对比图Fig.7 simulation comparison diagram of network model
3.2.3 天然径流量模拟结果与分析
由图7可以看出,把建立好的神经网络模型应用到本流域中,BP神经网络经过前35年的学习,在后十五年得到了很好的仿真效果,仿真模拟出的1991-2005年的天然径流量,并与当地水文局一块合作[13]提供的实测与计算出的天然径流量进行误差对比,来验证模型的准确合理性与实用价值。结果发现,预测误差均在合理范围内,方法可行可靠[14,15]。其中,误差在5%以下的有10年,误差百分比在5%~10%之间的有4年,误差大于10的有一年,2005年,需要进一步完善。具体模拟结果见表5。

表4 BP模型参数的选取Tab.4 BP Model parameters selection
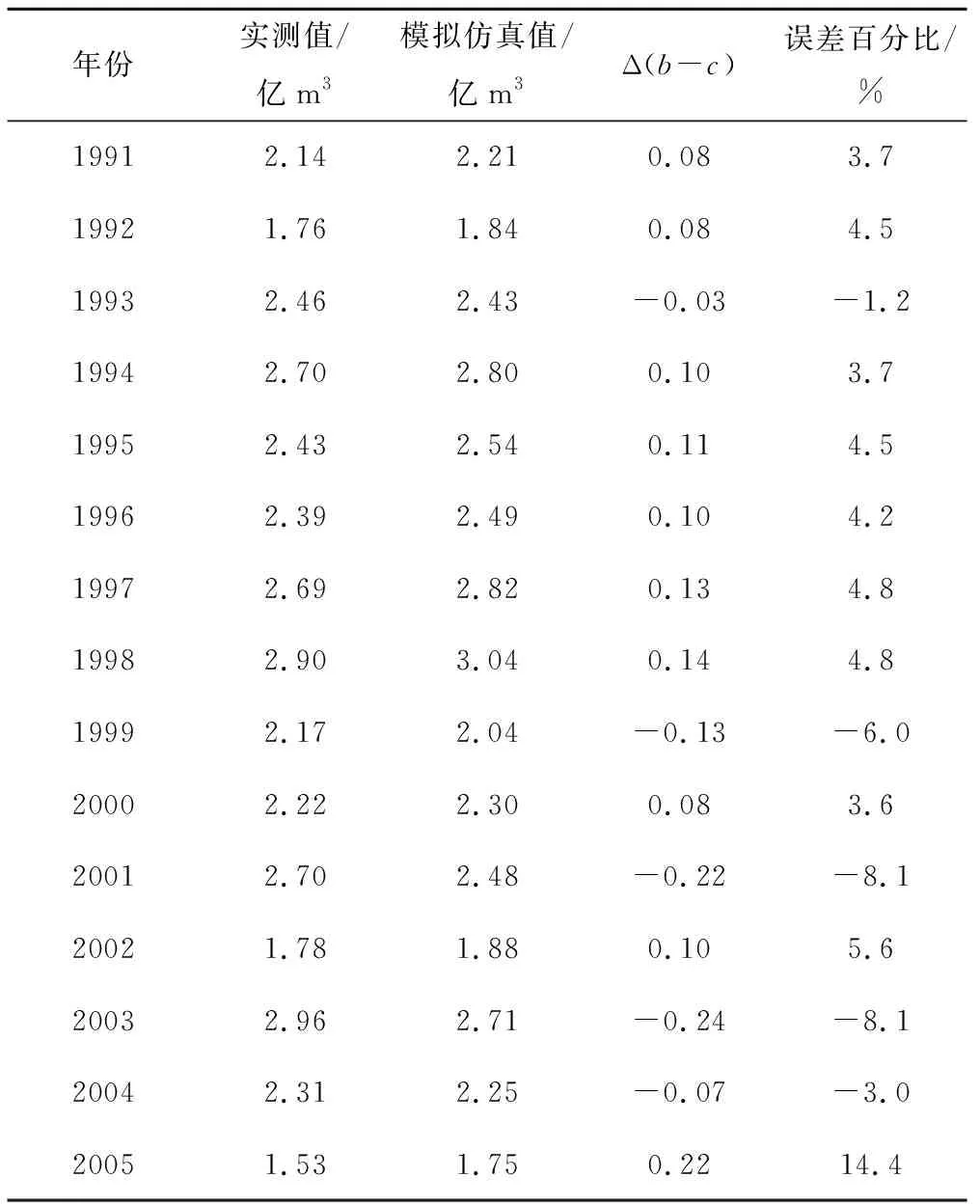
表5 网络的仿真对比图表Tab.5 Simulation comparison table of network
4 结 论
(1)本文建立了RVA模型对烟台大沽夹河流域外夹河水文情势进行分析研究,得到了月平均流量、日极限流量等参数发生中度改变,水利工程的修建产生的影响比较大,当地水文情势发生比较大的改变。
(2)在RVA模型研究的结论为基础,并在充分理解河川径流的形成机制和传统的求解河道天然径流的还原计算方法的基础上,将人工神经网络系统中的BP算法移植到河道水量的还原计算上,把这两个方法创新性地进行了结合,用历史资料先进行学习、在仿真检验最终做预测,通过预测结果进行误差对比,结果发现,BP神经网络对天然经流量还原的方法,可误差在合理范围内,可以应用到大沽夹河流域河道水量的还原计算上,精度较好,效率较高。
(3)模型在精度上还有提升完善的空间,需进一步优化设计组合模型,本次研究是对逐年的天然径流量还原计算,在后续研究中可以尝试逐月天然径流量的还原计算,进一步细化和丰富研究。
□
——电影《郭福山》主题歌(男中音独唱)

