PSO算法与DDS算法在EasyDHM模型中的参数分析及对比研究

卢思成，廖卫红，雷晓辉，殷兆凯，王 浩

(1. 北京工业大学建筑工程学院，北京100124；2.中国水利水电科学研究院水资源研究所, 北京100038； 3．天津大学建筑工程学院，天津 300072)

EasyDHM模型(Easy Distributed Hydrological Model)[1-3]是由雷晓辉等人开发的在国内适用性较高、扩展性较强的分布式水文模型。EasyDHM模型的原理和在各流域的适用性已有了较多研究[4-7]，但很少有人从EasyDHM模型参数率定角度开展研究。一方面，随着变化环境影响的不断深入，水文模型产汇流参数变化幅度更为剧烈，对参数率定算法也提出了更高的要求。为了提高该模型水文预报的精度，仍需不断对模型原有的优化算法进行改进，并探索和引入更高效的优化算法。

粒子群优化算法(Particle Swarm Optimization Algorithm，PSO)[8,9]是一种进化计算机技术，该算法原理简单易于实现可用于解决大规模、非线性、不可微和多峰值的复杂优化问题，但是该算法和其他全局优化算法一样，可能陷入局部最优，导致后期收敛精度不高，收敛速度较慢[10]。动态维度搜索(Dynamically Dimensioned Search，DDS)[11]是一种随机搜索启发式算法，该算法能快速高效地收敛于全局最优解[12]，计算效率与传统的优化算法如遗传算法相比更高[13]。EasyDHM模型已经内置了DDS算法，且DDS算法现在已经在EasyDHM模型的参数率定上得到了广泛的应用，但还没有人对该算法在EasyDHM模型上的进行模型参数率定时的算法参数设置进行研究。为了进一步提高EasyDHM模型的参数率定的性能，本文将分析DDS算法的参数设置对EasyDHM模型参数率定效果的影响，同时引入PSO算法与DDS算法进行对比，也对PSO算法的参数设置对EasyDHM模型参数率定效果的影响进行分析，从而找到两种算法在EasyDHM模型上进行参数率定的最优算法参数。对比两种算法在最优算法参数下的率定效果，从而找到在不同的应用情况下，推荐的EasyDHM模型参数率定算法。

1 EasyDHM模型

本研究选用EasyDHM模型对汉江丹江口水库以上流域的水文模型进行构建，EasyDHM模型支持多种产汇流计算算法，本研究采用EasyDHM产流模型进行产流计算，采用马斯京根法进行汇流计算。

EasyDHM模型中涉及的参数很多，共包括49个参数，对这些参数都进行参数率定是不现实的，本文对模型的主要参数包括主要全局产流参数、主要子流域修改参数和主要汇流参数在内的共27个参数进行参数率定[2]。参数的物理意义、上下限如表1所示。

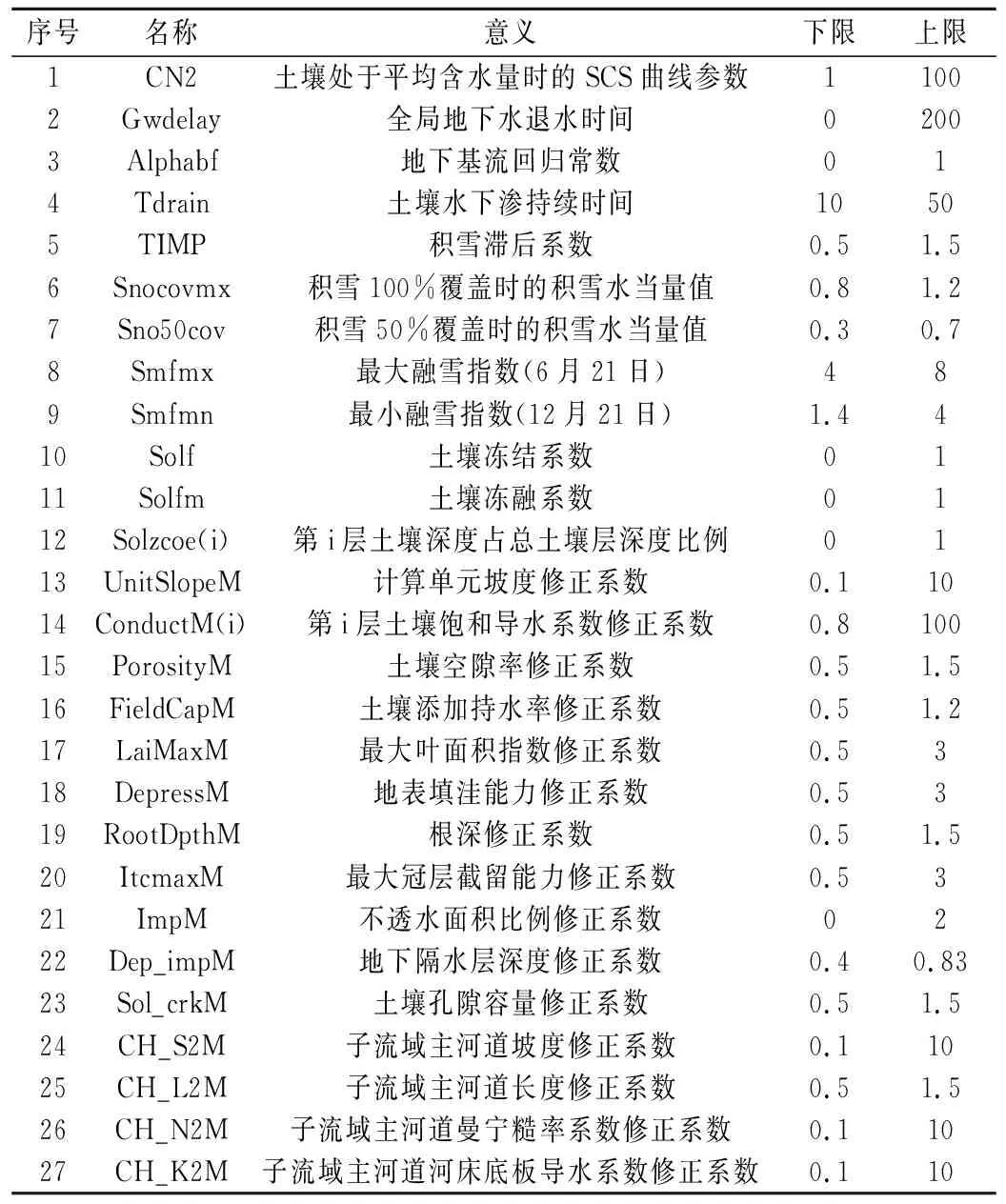
表1 参数的物理意义和上下限Tab.1 The physical meaning,upper limits and lower limits of the parameters

2 分析指标与模型算法

2.1 分析指标

本文采用的水文模拟精度评价分析指标包括水量平衡误差、纳什效率系数、洪峰流量误差和峰现时间误差4个指标。纳什效率系数同时作为两种优化算法的目标函数使用。

(1)水量平衡误差。水量平衡误差表示模型的径流模拟值与实测值之间的差与实测值的比。其方程表示如下：

(1)

式中：EQ(无量纲)代表水量平衡误差；Qto和Qtm分别代表对i时刻径流量的实测值和模拟值，m3/s；N(h)是整个模拟时间段的总长度。EQ取值为正无穷到负无穷，EQ越接近0说明误差越小 。

(2)纳什效率系数。纳什效率系数衡量模型模拟径流的好坏程度。方程表示如下表示：

(2)

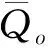
(3)洪峰流量误差。洪峰流量误差即为计算洪峰流量与实测洪峰流量的差与实测洪峰流量的比。方程表示如下：

(3)

式中：Ep(无量纲)是洪峰流量误差；Qsp是模拟洪峰流量，m3/s；Qop是实测洪峰流量，m3/s。Ep取值为正无穷到负无穷，Ep越接近0说明误差越小。

(4)峰现时间误差。峰现时间误差Etime(h)反映模拟洪峰出现的时间与实测洪峰出现的时间的差距，Tmp为模拟峰现时间，Top为实测峰现时间。Etime取值为正无穷到负无穷，Etime越接近0说明误差越小。方程表示如下：

Etime=Tmp-Top

(4)

2.2 PSO算法

PSO算法在1995年由Kennedy博士和Eberhart博士提出，源于鸟群捕食行为研究。粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子具有速度v和位置x两种属性。每个粒子在搜索空间中单独搜寻最优解，并将其记为当前个体历史最优解xpbest，并将个体历史最优解与整个粒子群里的其他粒子共享，找到最优的个体历史最优解作为整个粒子群当前的全局历史最优解xgbest，粒子群中的所有粒子根据自己找到的当前个体历史最优解xpbest和整个粒子群共享的当前全局最优解xgbest来调整自己的速度和位置，就这样通过群体中个体的信息共享使整个群体的运动在问题的求解空间中产生从无序到有序的演化。该算法的算法流程为：

(1)根据实际问题确定目标函数，设置算法的进化代数、种群数、惯性权重和加速度常数，在参数的取值范围内随机生成各粒子的初始位置和速度。

(2)把各粒子代入模型中，计算各粒子的适应值。将粒子当前的适应值与粒子的个体历史最优适应值比较，如果当前适应值更优，则将当前粒子的位置作为粒子的个体历史最优解，如果粒子的个体历史最优适应值更优，则保留原个体历史最优解不变。

(3)将各粒子的个体历史最优适应值与全局历史最优适应值比较，如果某粒子的个体历史最优适应值更优，则将该粒子的个体历史最优解作为全局历史最优解，如果全局历史最优适应值更优，则保留原全局历史最优解。

(4)根据如下速度公式和位置公式对粒子的位置和速度进行更新。

速度更新公式：

vi(t+1)=wvi(t)+C1r1[xpbesti(t)-xi(t)]+

C2r2[xgbest(t)-xi(t)]

(5)

式中：vi=(vi1，vi2，…，viD)和xi=(xi1，xi2，…，xiD)分别表示粒子在D维空间的速度和位置,v、x的计量单位根据率定的参数的不同而不同；vi(t+1)表示第i个粒子下一次运动的速度；第一部分wvi(t)是惯性量，是延续粒子上一次运动的矢量，w是惯性权重，无量纲，取小于1的数，vi(t)表示第i个粒子本次运动的速度；第二部分C1r1[xpbesti(t)-xi(t)]是个体认知量，是向个体历史最优位置运动的量，xpbesti是当前第i个粒子的个体最优解，xi(t)是当前第i个粒子的位置，r1是一个[0，1]的随机数，无量纲，C1是加速度常数，无量纲，通常取C1=2；第三部分C2r2[xgbest(t)-xi(t)]是社会认知量，是粒子向全局最优位置运动的量，xgbest(t)是当前全局最优解，r2是一个[0，1]的随机数，无量纲，C2是一个加速度常数，无量纲，通常取C2=2。

位置更新公式：

xi(t+1)=xi(t)+vi(t)

(6)

式中：xi(t+1)表示第i个粒子下一次运动的位置，其他变量含义与式(5)相同。

为了防止粒子远离搜索区域，设定vi的取值范围为[-vmax，vmax]，xi的取值范围为[-xmax，xmax]，v=kxmax，其中0. 1≤k≤1. 0，无量纲。

(5)判断粒子是否收敛或者达到最大迭代次数，如果没有，则重复步骤(2)～步骤(5)直到收敛或者达到最大迭代次数后输出最优解。

本文将研究PSO算法的几个重要的参数：惯性权重、加速度常数、种群规模和进化代数对PSO算法率定EasyDHM模型参数性能的影响并找到最佳的PSO算法参数设置。

2.3 DDS算法

DDS算法在2007年由tolson与shoemaker提出的一种随机搜索启发式算法，该算法能快速收敛于最优解[13]，算法的搜索策略为先全局后局部，通过从全部参数中随机、动态地选择若干参数进行参数率定以寻找新的候选解进而不断更新当前最优适应值和最优解[14]。算法的流程为：

(1)根据实际问题确定目标函数，确定扰动参数r，最大迭代次数m，每一个参数的上下限Xmaxi和Xmini，在参数的取值范围内随机生成初始解向量。

(2)将初始解向量代入模型，计算适应值，将其设置为当前最优解。

(3)在D个维度中，随机选取J个维度建立新的解的邻域[N]，计算[N]中每一个参数发生变化的概率P(i)，将解向量中各维度以P(i)的概率加入[N]，当[N]为空时，随机选取一个维度加入[N]。

(4)对于[N]中的维度，通过以下公式对最优解Xjbest加入扰动，该扰动符合标准正态分布N(0，1)。

Xj(t+1)=Xbestj+r(Xmaxj-Xmaxj)N(0,1)

(7)

式中：Xj(t+1)表示加入扰动后的解；Xbestj表示当前最优解中j所代表的维度的参数值，计量单位根据率定的参数的不同而不同。r为扰动参数，无量纲。

(5)将加入扰动后的解向量代入模型，计算适应值，如果用加入扰动后的解向量代入模型计算出的适应值大于用当前最优解代入模型计算出的适应值，则设置加入扰动后的解向量为最优解；如果加入扰动后的解向量代入模型计算出的适应值小于用当前最优解代入模型计算出的适应值，则保留当前最优解。

(6)判断粒子是否收敛或者达到最大迭代次数，如果没有，则重复步骤(3)～步骤(6)直到收敛或者达到最大迭代次数后输出最优解。

本文将研究DDS算法的两个重要参数：扰动参数和最大迭代次数对DDS算法率定EasyDHM模型参数性能的影响并找到最佳的DDS算法参数设置。

3 DDS算法与PSO算法的EasyDHM模型参数率定

3.1 EasyDHM建模

本文的研究区域为汉江丹江口以上流域，汉江位于我国中部地区，是长江最大的一级支流，该流域位于湖北南北过渡、承东启西的地带，地形上兼备山区和平原，具有两种地形的气候特点，每年降水约873 mm，水量充沛；但丰水期降水远多于枯水期，降雨年内分配不均，丰水期流量大约占全年1/4，年际变化较大，是变化最大的长江支流。本研究采用区域内的5个水文站，8个气象站和187个雨量站的水文资料。流域概况和各站点分布见图1。

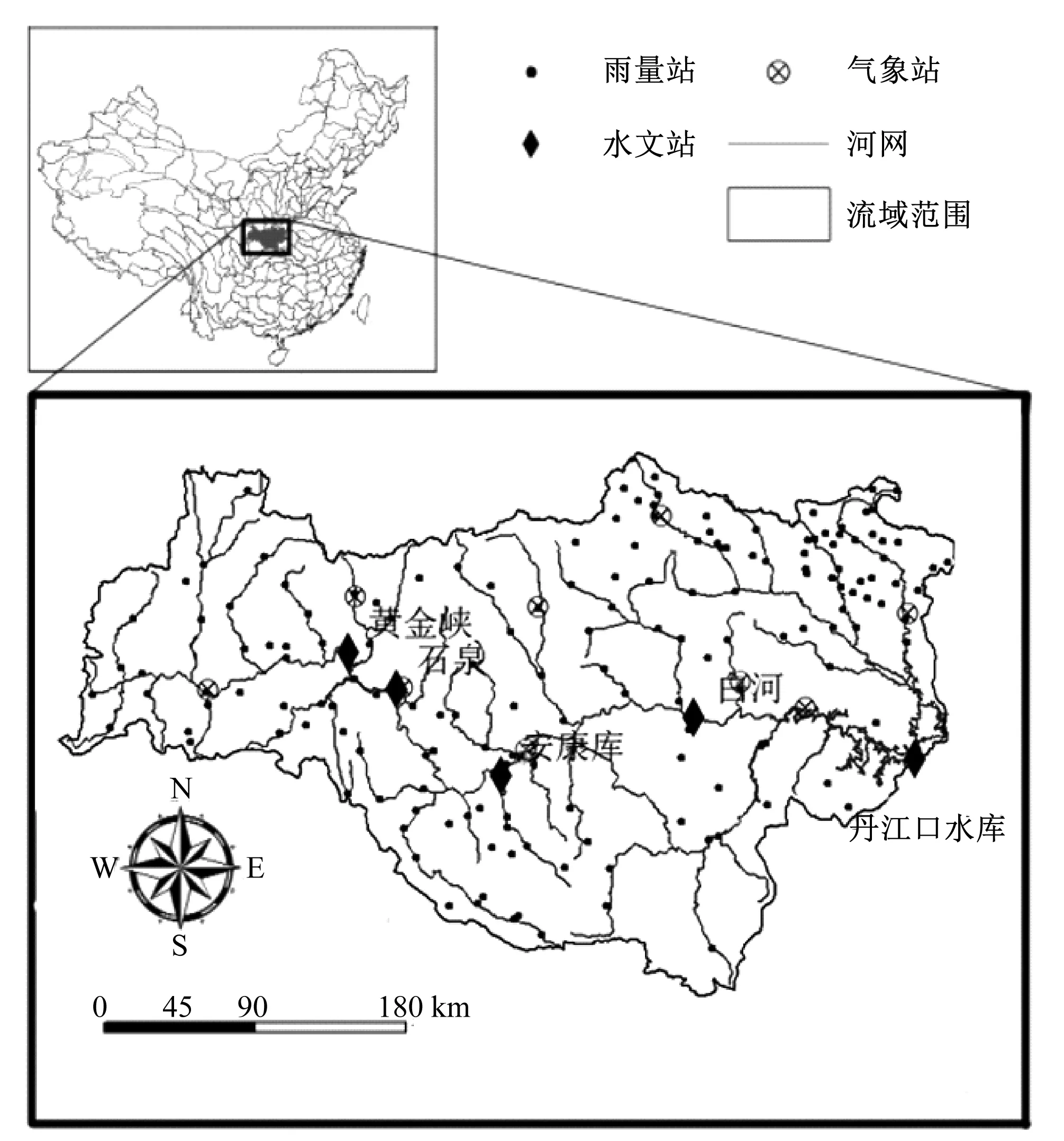
图1 流域概况Fig.1 General situation of basin

本文使用的原始DEM数据来自美国联邦地质调查局(USGS)的HYDRO1k。依据实际河网对原始DEM进行修正后，再进行填洼、生成流向、计算流入累计数和提取河道计算，得到水系河网。

土地利用信息为全国分县土壤覆盖矢量数据，该数据属于《全国资源环境遥感宏观调查与动态研究》课题的研究成果[15]。从中提取出的汉江流域土地利用图。土壤基础信息基本矢量图为第二次全国土壤普查的《1：100万中国土壤分类图》。土层厚度及土壤质地信息源于《中国土种志》。汉江丹江口以上流域EasyDHM模型建模采用流域内的5个水文站2012-2014年的实测洪水3 h时段流量过程资料、8个气象站2012-2014的气温、日照、湿度及风速的日观测资料和187个雨量站2012-2014年的3 h雨量观测资料，流域平均降雨量通过泰森多边形法计算得到。

汉江流域雨量站和水文站数量较多，本文仅以汉江流域丹江口水库以上汉江干流的黄金峡、石泉、安康、白河、丹江口5个断面2012-2014年共16场不同量级的有代表性的洪水作为对象，来分析采用DDS算法和PSO算法对EasyDHM模型进行参数率定的过程及结果，断面相关数据见表2，洪水基本信息见表3，有上游水文站的断面采用上游断面的预报结果作为上游入流。每个参数分区在2012至2014年间选取典型洪水进行参数率定，时间尺度为3 h。

表2 研究站点基本信息Tab.2 Basic information of study station

由于优化算法都存在着一定的随机性，为了尽量减少随机性的影响，每场次都在同样条件下率定10次，取率定效果最好的一次结果作为该场次的率定结果，统计每种优化算法在不同参数下所有站点所有洪水的目标函数的平均值，根据目标函数的平均值对不同算法参数下模型的参数率定性能进行分析。最后比较两种算法在最优参数下率定的效果。

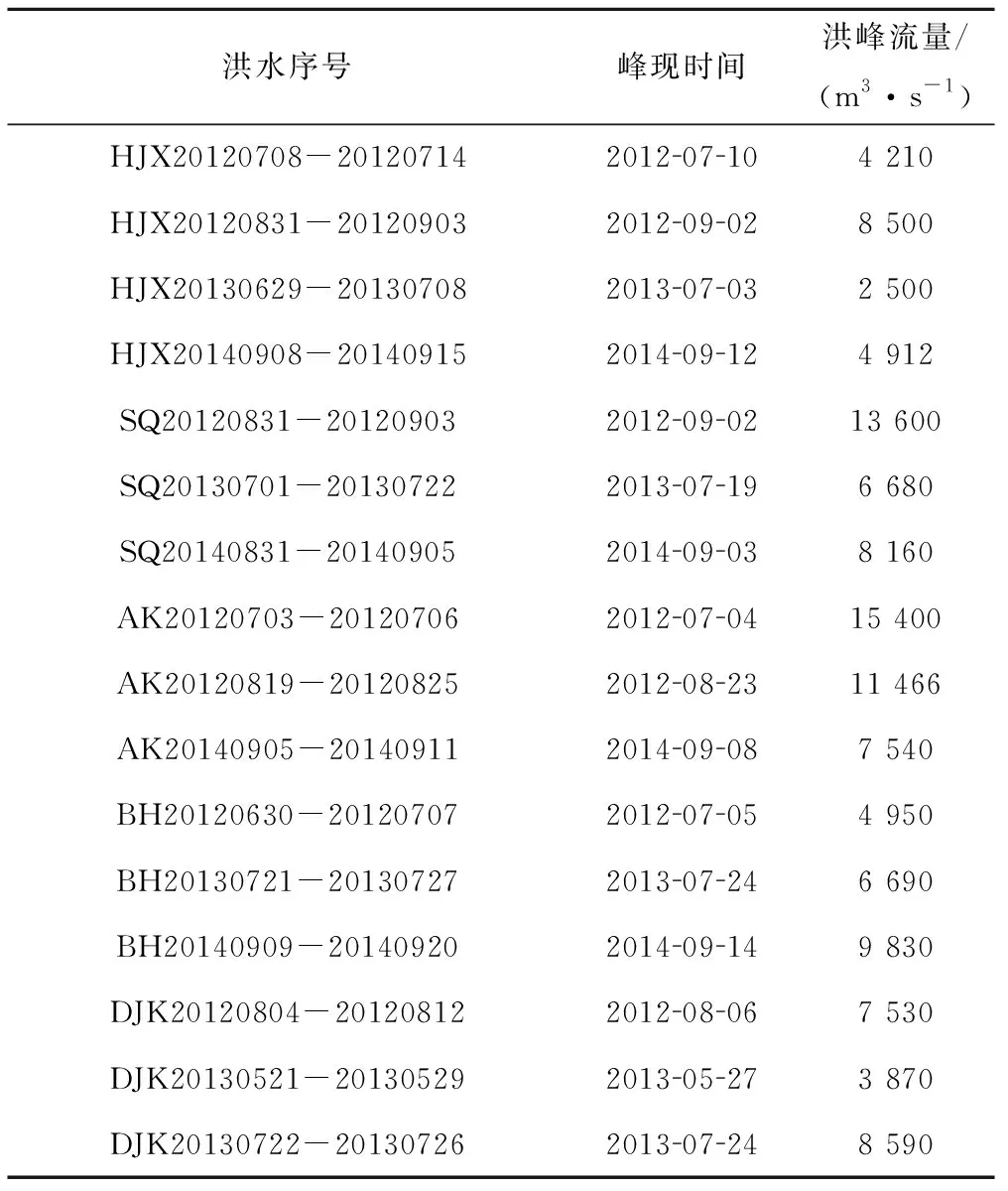
表3 洪水基本信息表Tab.3 Basic information of floods

3.2 PSO算法的参数率定

3.2.1 种群规模与进化次数的影响分析

PSO算法在EasyDHM模型这样的参数众多的分布式水文模型上进行参数率定难以达到完全收敛，因此需要对种群规模和进化代数这两个与算法性能关系最为密切的算法参数进行研究来寻找一个在算法未完全收敛的情况下使模型参数率定性能最高的算法参数设置方法。PSO算法的其他参数设置为：加速度常数C1=C2=2，惯性权重w=0.5。由于EasyDHM模型参数较多，在进化代数和种群数都大的情况下率定耗时过长，没有实际意义，因此本文不对两者都较大的情况进行探讨。种群规模和进化代数以及目标函数分析均值结果见表4。

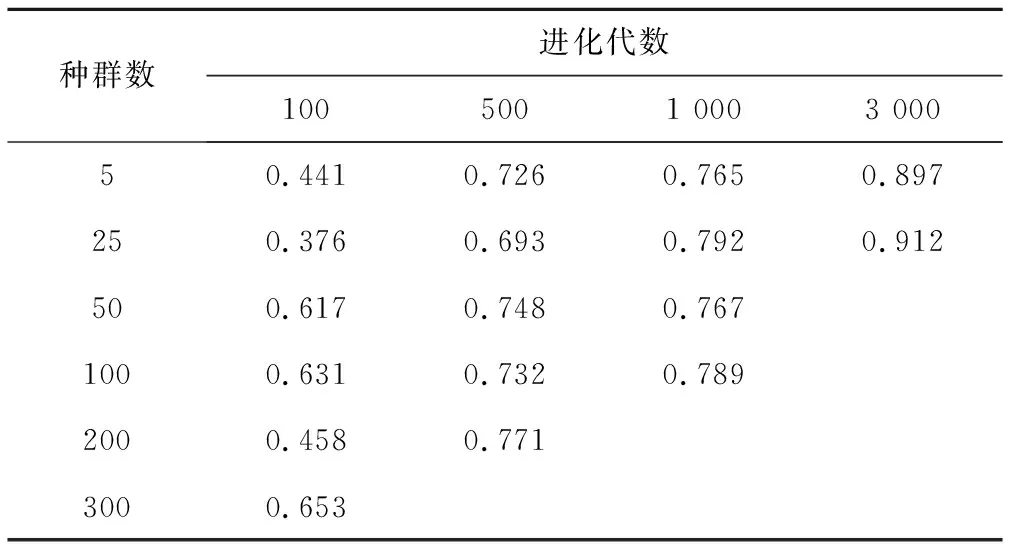
表4 不同种群规模和进化代数下各方案所有场次洪水目标函数均值Tab.4 Average of objective function of all floods of every solution under different population size and evolutionary generations

从表4可知，总体上种群数和进化次数越大算法的效果越好。在种群数一定的情况下，增加进化次数可以看到目标函数有明显的提高，而在进化代数一定的情况下增加种群数虽然对目标函数有提高有帮助但效果并不明显。需要提出的是，种群数300，进化100代时运算的时间已经大约是种群数5进化3000代时的2倍，说明在EasyDHM模型上最高效的算法参数设置方法是小的种群规模和较高的进化代数。另外虽然种群数和进化代数都大时参数率定的效果会更好，但由于率定耗时过长而没有实际意义。因此就EasyDHM模型而言，进行场次洪水参数率定建议的参数设置为种群数25，进化3 000代左右。

3.2.2 加速度常数C1和C2的影响分析

其他参数设置为种群数25，进化3 000代，惯性权重取w=0.5，加速度常数取根据过去的研究取C1+C2=4[10,16-18]。C1分别取0，0.5，1，1.5，2，2.5，3，3.5，4一共9种方案进行实验，得到的目标函数均值见表5。

表5 不同加速度常数下各方案所有场次目标函数均值Tab.5 Average of objective function of all floods of every solution under different Acceleration constant

C1越大表示粒子的搜索越依赖个体认知，即依赖当时的个体最优解，在C1+C2=4的条件下C1越小表示粒子的搜索越依赖社会认知，即依赖当时的全局最优解。由表4可知，无论是过多依赖个体认知还是过多依赖社会认知，都会对算法的性能产生负面影响，而当二者接近平衡时能算法性能最好，因此就EasyDHM模型而言，进行场次洪水参数率定建议的加速度常数C1取值为[1，3]。

3.2.3 惯性权重w的影响分析

其他参数设置为种群数25，进化3 000代，加速度常数C1=C2=2。w分别取0.1，0.3，0.5，0.7，0.9一共5种方案进行实验，得到的目标函数均值见表6。

表6 不同惯性权重下各方案所有场次目标函数均值Tab.6 Average of objective function of all floods of every solution under different inertia weight

由表6可知，惯性权重的改变对参数率定的结果的影响与其他参数相比较小，当该值取0.5和0.7时算法的性能要优于其他取值。因此就EasyDHM模型而言，进行场次洪水参数率定建议的惯性权重[0.5，0.7]。

3.3 DDS算法的参数率定

与PSO算法相比，DDS算法在参数众多的EasyDHM模型中仍然可以实现短时间内完全收敛，因此对最优算法参数的选取同时考虑目标函均值和达到完全收敛所需要的迭代次数两个因素。研究方案的参数设置和目标函数均值分析见表7。

由表7可知，当扰动参数处于高值和低值时，算法的性能都有显著的下降，特别是处于高值的0.8时，进行6 000次迭代算法仍然没有达到完全收敛且率定效果不好。当扰动参数为[0.4，0.6]时，算法能够在4 000次迭代之前达到完全收敛，算法性能要优于常用值0.2。因此在EasyDHM模型的参数率定中DDS算法推荐使用的扰动参数为[0.4，0.6]，建议采用的迭代次数为[1 000，2 000]。

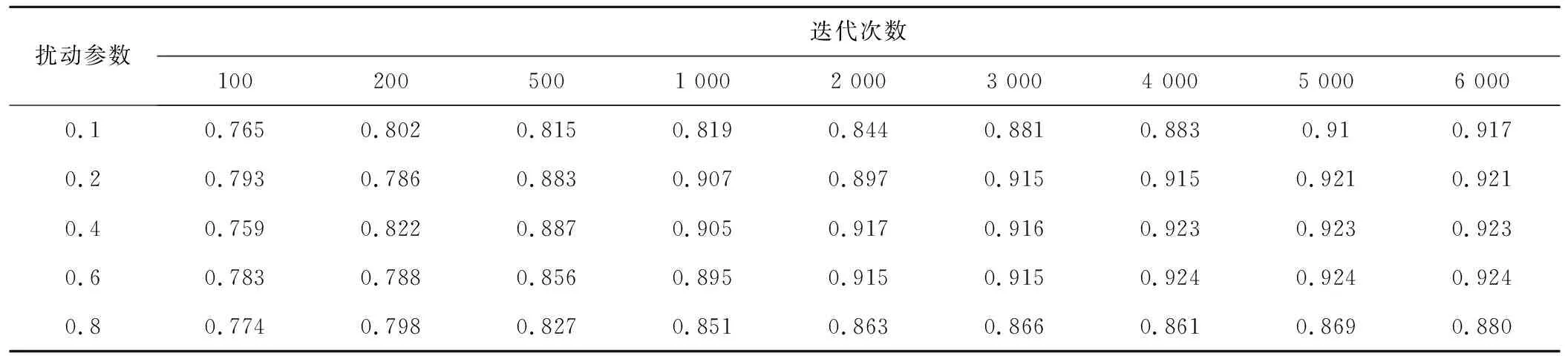
表7 不同扰动参数与迭代次数下各方案所有场次目标函数均值Tab.7 Average of objective function of all floods of every solution under different disturbance parameters and iterations

3.4 率定效果对比分析

通过对两种算法的参数进行分析，得到了两种算法在EasyDMH模型上进行率定的最优参数设置方案，为了对比两种算法在该模型上进行参数率定的性能，选用两种算法在最优参数下对汉江流域丹江口水库以上汉江干流5个断面的16场洪水的率定结果进行对比。参数设置为PSO算法：加速度常数C1=C2=2，惯性权重w=0.5，进化3 000代，种群数25；DDS算法：扰动参数r=0.4，迭代3 000次。两种算法都运行10次，取率定效果最好的一次作为该场次洪水率定的结果，分析结果见表8，部分场次洪水率定效果见图2。

由表8可知，使用DDS算法进行参数率定时，大部分场次的目标函数在0.8以上，使用PSO算法进行参数率定时所有场的目标函数均在0.8以上，说明使用DDS算法和PSO算法在EasyDHM模型上进行参数率定都能得到较好的效果。根据所有场次洪水的各指标均值可知在以纳什系数和水量平衡误差为主要评价标准时，采用DDS算法能得到较好的效果，而在以洪峰流量和峰现时间为主要评价标准时，采用PSO算法能得到较好的效果。根据所有场次洪水的各指标方差可知PSO算法稳定性要略优于DDS算法，但两者差别不大。分析各区域的洪水率定结果，发现汉江上游的率定效果总体上要优于中游，这可能是因为汉江流域水库较多，由于资料限制没能很好地考虑各水库的调度产生的误差，这是今后进行研究时需要改进的地方。

各场次洪水计算结果表明，虽然前文提到了DDS算法可以在EasyDHM模型的参数率定中较短时间内达到收敛，而PSO算法要达到收敛较为困难，但是并不代表完全收敛时的DDS算法率定效果一定会优于未收敛时的PSO算法，原因在于优化算法可能会陷入局部最优。另外需要提出的是两种算法分别在最优参数下运行时，单次运行PSO算法所花费的时间比DDS算法更长。

图2 洪水过程模拟结果对比图Fig.2 Comparison of the simulation results of the flood process

DDSNESEQEtime/hEpPSONESEQEtime/hEpHJX20120708-201207140.976 0.0110-0.057 0.950 0.025 00.072 HJX20120831-201209030.961 0.0010-0.099 0.960 -0.005 00.057 HJX20130629-201307080.887 -0.01430.172 0.873 -0.024 60.035 HJX20140908-201409150.950 0.0010-0.074 0.946 0.005 0-0.126 SQ20120831-201209030.983 -0.0010-0.065 0.979 -0.016 0-0.050 SQ20130701-201307220.844 0.011-60.177 0.894 0.027 -30.117 SQ20140831-201409050.962 -0.002-6-0.138 0.965 -0.007 0-0.074 AK20120703-201207060.971 -0.00430.097 0.961 -0.006 3-0.052 AK20120819-201208250.965 0.01300.081 0.897 0.013 00.091 AK20140905-201409110.8850.011-60.1510.871-0.02230.159BH20120630-201207070.951 -0.006-30.094 0.932 0.008 -30.118 BH20130721-201307270.862-0.021-60.148 0.889 0.034 -60.084 BH20140909-201409200.791-0.03890.2940.806-0.093120.137DJK20120804-201208120.818 -0.0133-0.149 0.830 -0.045 3-0.085 DJK20130521-201305290.8710.0160-0.1620.862-0.0780-0.128DJK20130722-201307260.9470.01500.0930.9370.01600.072绝对值的均值0.9160.011 2.810.1280.9120.0272.4420.091绝对值的方差0.0040.001 6.1540.0030.0030.0015.8720.001

4 结 论

本研究将PSO算法引入EasyDHM模型，并与模型内置的DDS算法进行对比，研究解决多参数分布式水文模型的参数率定问题。主要结论如下：①把算法应用在一种新的模型上时算法给出的默认参数不一定适用，本文通过对DDS算法和PSO算法的参数进行分析给出了在EasyDHM模型上进行时段长为3小时的场次洪水参数率定建议的算法参数选取方案，该算法参数选取方案在除此之外的情形下不一定适用，但可以作为算法参数选取的参考使用。②将两种算法应用在汉江丹江口以上流域EasyDHM模型的参数率定上，总体上都表现了较好的适应性。③通过对比分析两种算法在最优参数下进行参数率定的效果给出了用EasyDHM模型进行场次洪水预报时，参数率定算法选择的建议：在要求率定效果最好情况下，预报的主要指标为洪量时建议使用DDS算法，预报的主要指标为洪峰是建议使用PSO算法；在要求率定速度尽量快，且率定效果比较好的情况下，建议使用DDS算法。

□