基于SPH的浮式防波堤消波效果分析研究

陈 阳，陈 鑫，李 千，陈 程，崔 杰

（江苏科技大学 船舶与海洋工程学院，江苏镇江 212003）

0 引言

浮式防波堤是一种重要的港口水工结构物，用于防御外海传来的波浪。波浪从深水传播到近岛礁水域，受地形的影响，波浪特征会出现较大的变化，水质点与浮体、地形发生摩擦、扰流和碰撞，其运动规律受到破坏，复杂环境条件下防波堤会呈现强非线性耦合运动。HEGDE等[1]研究了一种圆管堆砌而成的新型浮式防波堤，其主要工作是计算当圆管间距与圆管直径比分别为2、4时的迎浪一侧系泊缆的张力幅值，计算结果表明：圆管间距和圆管直径的比值越大，张力幅值越小。KORAIM[2]开发了一种新型圆筒管式浮式防波堤，主要结构型式为单层或多层的类似于圆管的结构，进行水槽试验后发现，管式结构布置的越多、越密，浮式防波堤的透射波高与入射波高的比值越小，消波效果越明显。吴广怀等[3]基于势流理论，建立模型分析了浮式防波堤改变浮体之间距离后的水动力性能。陈力[4]进行了模型试验，将浮箱式浮式防波堤固定在水面上，研究波浪作用下防波堤的水动力性能，通过仪器测出堤体表面测点的压力，绘制压力分布曲线。王科、贺大川等[5]建立的防波堤模型的水下部分采用板式结构，水上部分采用浮筒结构，其主要采用边界单元法在对模型进行网格划分后分析波浪作用下的水动力性能。盛祖荫和孙龙[6]通过改变浮箱式浮式防波堤的阻挡波浪部分的尺寸大小，在进行试验研究后发现：透过防波堤的波浪波幅会随着这部分面积的大小而变化。邹志利等[7]通过改变不同入射波基本参数、调整防波堤不同入水高度，对固定不动的浮式防波堤进行了试验研究，得出了一系列试验结果。

SPH方法是基于流体动力学理论的无网格的光滑粒子法。REN等[8]在研究波浪与多孔结构的相互耦合作用时，应用SPH方法成功模拟了波浪在可透海底传播的过程。GOTOH等[9]基于SPH理论研究了波浪破碎在海岸工程领域的作用。姜峰等[10]基于SPH理论研究了波浪与沉箱式防波堤的耦合作用。王烨和王永学等[11]研究了在SPH数值环境下双方箱浮式防波堤在不同锚固方式下的水动力特性的模拟。MONAGHAN[12]基于SPH方法模拟了不同波浪的破碎情况和遇到岛礁时的爬坡现象。

目前，一些商业软件（如AQWA、SESAM等）可以模拟简单地形对系泊式结构物水动力性能的影响，但无法模拟地形变化引起的流体粘性运动，并且求解时没有考虑动态系泊锚链对其的真实作用，无法得到波浪演化情况。本文基于SPH流体动力学理论，编写浮式防波堤与系泊系统在波浪载荷下耦合运动计算程序，先对比不同周期下不同尺寸形式的浮式防波堤的透射系数，选取消波性能相对比较优秀的最优尺寸的浮式防波堤，再以此型浮式防波堤为参考，结合现实海况，为新型浮式防波堤设计提供理论依据。

1 数值模型

1.1 SPH基本方程

在SPH方法中，函数f(x)的积分表示式定义为

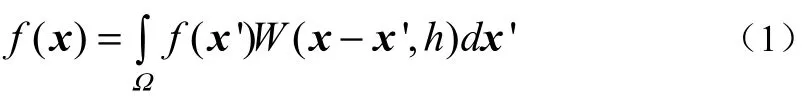
式中：x为位置向量；w为权重函数或内核；h为内核的半径。

f(x)的连续 SPH积分表达式可以写作以下离散化的粒子近似式。

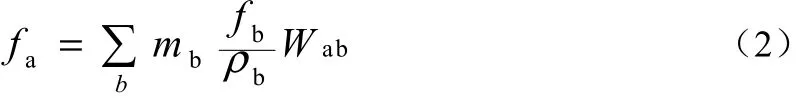
式中：mb表示相邻粒子的质量；ρb表示相邻粒子的密度；表示加权函数或者内核。

1.2 Navier-Stokes方程的SPH粒子近似式

流体运动采用 Navier-Stokes方程组来描述，Navier-Stokes方程可写成以下粒子近似方程（不考虑黏度）。

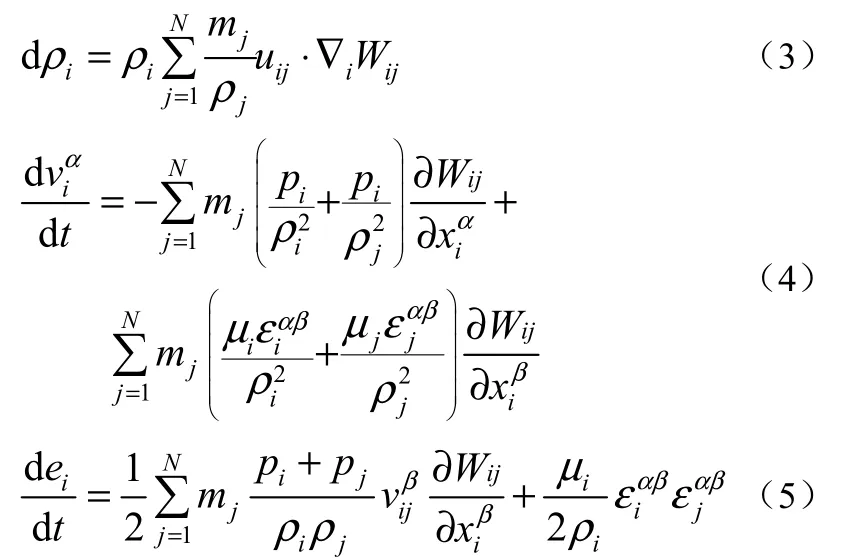
式中：ρi为粒子i的密度；ρj为粒子j的密度；t为时间；N为粒子i的支持域中粒子的总数；uij=ui－uj为粒子i和j之间的相对速度；Wij为粒子j对粒子i产生影响的核函数；αβ表示坐标方向；p为压力；ε为剪切应变率；μ为动力黏性系数；e为单位质量物质的内能。

1.3 边界条件

将固壁边界离散成边界粒子，并假定边界粒子对靠近它的流体粒子施加一个大小适当的中心排斥力，以阻止流体粒子穿越固壁边界。对于边界粒子和流体粒子间隔距离r，每单位质量的力由Lennard-Jones势给出。

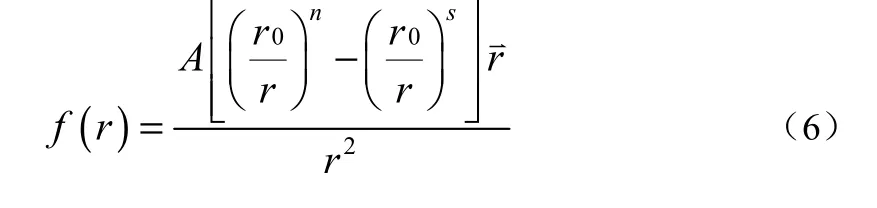
式中：A、n、s为可调参数；r0为粒子初始间距；r为当前时刻边界粒子和流体粒子的间距，r→为长度矢量。

1.4 浮体运动

对于浮体运动，使用基本的刚体运动方程，在自由平动和转动下，浮体的运动方程为

式中：M为浮体的质量；I为惯性矩；v为速度；Ω为旋转速度；R0为重心；在这种情况下，BPs表示边界粒子。

每个边界粒子有一个给定的速度，为

2 浮式防波堤消波性能分析

本节对堤宽分别为0.3 m、0.4 m、0.5 m的浮式防波堤消波性能进行了分析，分别建立不同工况下的数值模型，研究在不同工况下，浮式防波堤透射系数的规律。

如图1所示，浮式防波堤的堤宽分别为0.3 m、0.4 m和0.5 m。二维模拟数值水槽长度为18 m，最大工作水深d=0.6 m，推波板高度为0.72 m。定义粒子初始间距x=0.02 m，光滑长度h为0.92。时间步为满足CFL条件，定义Δt=0.000 2s。数值模拟水槽的右端设计坡角为 4.5°的斜坡消波层，浮体与水接触边界附加护壁虚粒子，设定坐标原点为水槽底部与推波板的交点，水平方向为x轴，竖直方向为z轴。计算总时间t=20 s，每0.02 s输出一次结果，共1 000步长。

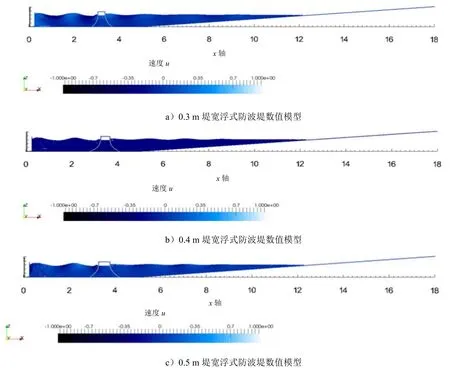
图1 浮式防波堤数值模拟

从图2可以看出：当波高为0.15 m和0.2 m时，浮式防波堤的透射系数随着波浪周期的增加而增加，不同堤宽下，防波堤透射系数随着堤宽的增加而减小。

图2 同波高下3种浮式防波堤透射系数随周期的变化

从图3可以看出：在1.0 s周期下，浮式防波堤的透射系数随着波高的增加先增加后减小，大约在波高为 0.15 m时达到峰值，由于入射波的增加不仅增强了反射作用，而且增大了浮式防波堤的运动响应，波浪产生的能量更多的以动能的形式耗散；当波浪周期变为1.4 s时，随着波高的增加，透过堤体的波浪高度越来越大，防波堤的消波性能越来越差；当波高从0.15 m开始增加时，透射系数开始减小，这是因为过高的波浪直接涌上了堤体，波浪发生了破碎，故而透过防波堤的波浪能量受到一定的削弱，在同周期下，增加堤宽增加，透射系数减小。因此，随着堤宽的增加，防波堤周围受到波浪干扰的水域面积增大，因而透射系数减小，消波效果更优。

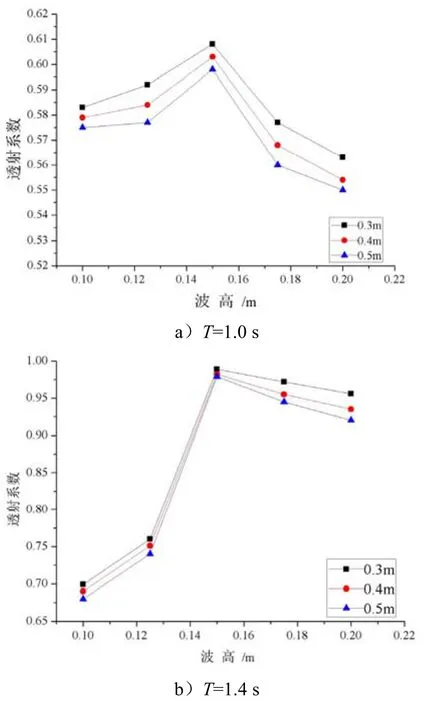
图3 同周期下3种浮式防波堤透射系数随波高的变化

3 结论

本文采用SP H数值方法，基于流固耦合力学理论，建立了浮式防波堤及系泊系统水动力分析方法，开展了对堤宽分别为0.3 m、0.4 m、0.5 m的浮式防波堤的水动力分析研究，得到如下结论：当入射波浪基本参数不变时，浮式防波堤的堤体宽度很大程度地影响透射系数的变化；当堤宽在一个合适的范围内逐渐增加时，浮式防波堤透射系数逐渐减小，消波效果也逐渐明显。本结论可为浮式防波堤的设计提供参考。