超临界二氧化碳无水染色系统有效能分析

苏耀华， 郑来久， 郑环达， 闫 俊， 高世会， 王 健， 万 刚

(1. 大连工业大学 全国超临界流体无水染色技术研发中心， 辽宁 大连 116034； 2. 青岛即发集团股份有限公司， 山东 青岛 266221)

超临界CO2无水染色技术采用CO2代替水介质在超临界状态下对纺织品进行染色，具有上染速度快，匀染性和透染性好的优势[1-2]；染色结束后经过降温释压，可实现染料和CO2的回收利用，省去了烘干工序，缩短了工艺流程，节约了能源[3-4]；此外，CO2本身无毒、无味、惰性、不燃，染色时无需添加分散剂、匀染剂、缓染剂等各类助剂[5-6]，具有安全性能高、生产成本低的特点，充分体现了清洁化、绿色化、环保化的现代印染加工理念[7-8]。超临界CO2无水染色设备绝大部分为高温、高压容器[9]，染色工艺中涉及增压、加热、节流、制冷等复杂过程，该过程存在能量损失[10-11]。在现有染色工艺技术基础上，研究超临界CO2无水染色系统的能量利用，有助于该项染整技术的产业化推广。因此，本文提出超临界CO2无水染色系统有效能分析研究。

有效能分析主要用于各种热能动力及化工生产领域的能量分析，已有较多的研究文献[12-14]报道。本文基于大连工业大学自主研制的GM40-5型超临界CO2无水染色系统，运用有效能分析法对该染色系统的能耗进行计算分析[15-17]，以揭示染色过程中的能量损失原因，指出减少能量损失的途径，以提高超临界CO2无水染色系统的能量利用效率。

1 超临界CO2染色系统有效能分析

1.1 系统单元有效能平衡方程建立

图1示出超临界CO2无水染色系统工艺流程，染色系统主要由充气、冷凝、存贮、增压、加热、染色、分离等单元组成[18-19]。染色流程为：气态CO2经冷凝器冷凝成液态，由增压泵加压至临界压力以上，经换热器加热至临界温度以上达到超临界状态。超临界CO2流经染料釜携带染料至染色釜，并进行染色。染色完成后，超临界CO2与未上染染料混合物经节流阀减压降温，在分离釜中实现CO2与染料的分离。分离后的CO2气体经冷凝器重新冷凝成液体回收储存在储罐中，分离出的染料沉积在分离釜内以回收利用[20-21]。

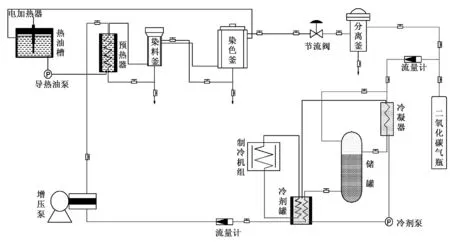
图1 GM40-5型超临界CO2无水染色系统工艺流程图Fig.1 Process flow diagram of GM40-5 supercritical CO2 anhydrous dyeing system

为便于对超临界CO2无水染色系统进行有效能分析，根据实际染色过程，对染色系统进行合理简化：忽略染料、被染物的影响，以CO2为计算工质进行系统有效能分析；染色过程能量供给来源于电能，忽略过程中化学有效能变化，染色单元与加热单元合并为加热/染色单元计算物理有效能；节流阀和分离单元合并为节流/分离单元计算物理有效能。因此，染色系统基本组成为增压单元、加热/染色单元、节流/分离单元、冷凝单元[22]4部分。简化后的超临界CO2无水染色系统如图2所示，对系统各个单元分别建立有效能平衡方程。

图2 超临界CO2无水染色系统Fig.2 System diagram of supercritical CO2 anhydrous dyeing

增压单元由柱塞式增压泵组成，作用为提高CO2的压力，使系统达到染色工艺压力条件，增压单元有效能平衡图如图3所示。

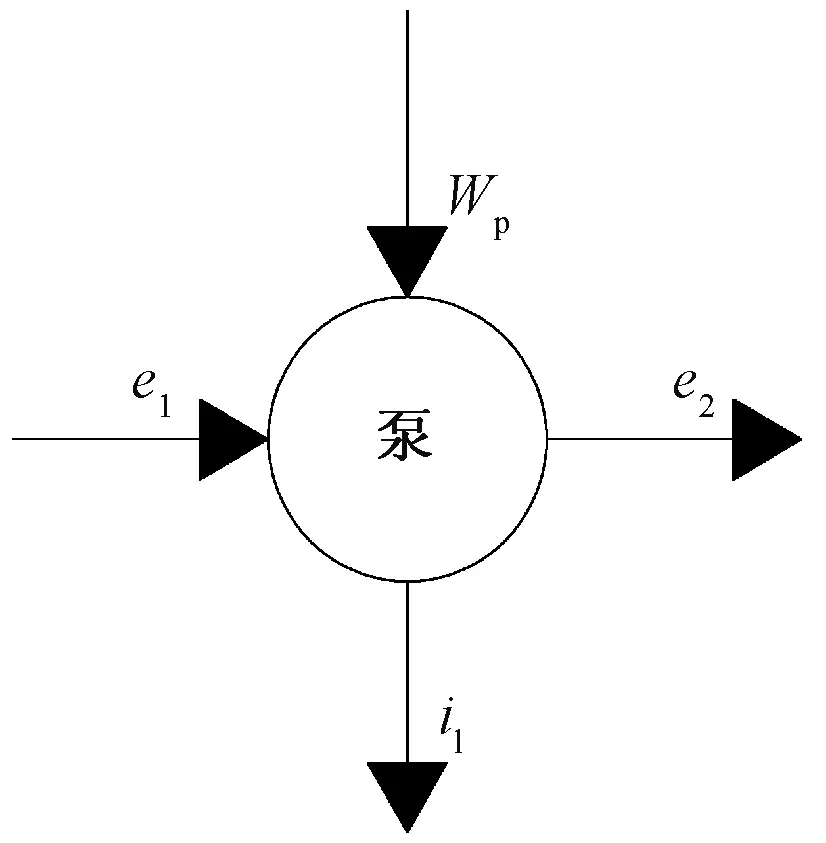
图3 增压单元有效能平衡图Fig.3 Available energy balance diagram of pressurized unit

其有效能平衡方程为

Wp+e1=e2+i1

(1)

式中：Wp为增压单元工质单位质量输入功，kJ/kg；e1、e2分别为增压单元进口、出口工质单位质量有效能，kJ/kg；i1为增压单元有效能损失，kJ/kg。

加热/染色单元是利用电加热器加热导热油为系统提供热量，使CO2达到临界温度以上，从而满足染色工艺条件进行染色。图4示出加热/染色单元的有效能平衡图。

图4 加热/染色单元有效能平衡图Fig.4 Available energy balance diagram of heating/dyeing unit

其有效能平衡方程为

Wq+e2=e3+i2

(2)

式中：Wq为电加热器工质单位质量输入功，kJ/kg；e2、e3分别为加热/染色单元进口、出口工质单位质量有效能，kJ/kg；i2为加热/染色单元有效能损失，kJ/kg。

节流/分离单元由节流阀和分离釜组成。染色完成后的CO2(含少许染料)经节流阀减压降温后，在分离釜中实现CO2和未上染染料的分离。在实际染色过程中，未上染染料较少，可忽略少量染料对系统有效能计算结果的影响，以CO2为工质计算节流/分离单元的有效能损失量，节流前后工质焓值不变，其有效能平衡图如图5所示。

图5 节流/分离单元有效能平衡图Fig.5 Available energy balance diagram of throttle/separation unit

节流/分离单元有效能平衡方程为

e3=e4+i3

(3)

式中：e3、e4分别为节流/分离单元进口、出口工质单位质量有效能，kJ/kg；i3为节流/分离单元有效能损失，kJ/kg。

制冷单元由制冷机组和冷凝器组成，主要作用为将已分离的气态CO2冷却成液态以供增压单元加压注入染色系统进行循环。储罐作用为存储液化后的CO2，其进出口前后工质状态变化不大，可忽略储罐的影响，制冷单元的有效能平衡图如图6所示。

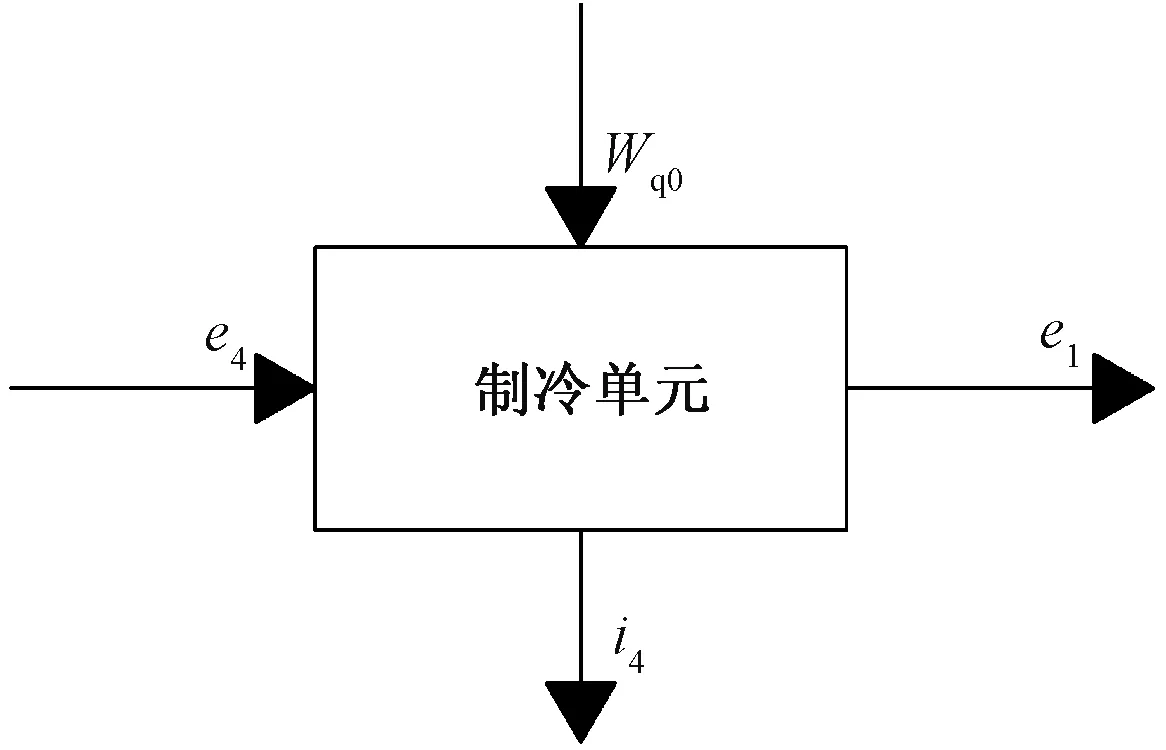
图6 制冷单元有效能平衡图Fig.6 Available energy balance diagram of refrigeration unit

其有效能平衡方程为

Wq 0+e4=e1+i4

(4)

式中：Wq0为制冷单元工质单位质量输入功，kJ/kg；e4、e1分别为制冷单元进口、出口工质单位质量有效能，kJ/kg；i4为制冷单元有效能损失，kJ/kg。

1.2 系统有效能计算分析

1.2.1稳流系统有效能表达式

稳流系统中工质由任意状态(T，P)变化到环境状态(T0，P0)时的单位质量有效能 (ex)定义[16]为

ex=h-h0-T0(s-s0)

(5)

式中：h、h0分别为工质在状态(T，P)、环境状态(T0，P0)下的比焓，kJ/kg；s、s0分别为工质在状态(T，P)、环境状态(T0，P0)下的比熵， kJ/(kg·K)；T0为环境温度，K。

1.2.2状态方程和计算方法

利用测温热电偶和压力变送器测量各个位置点的温度、压力值。在上述各单元有效能平衡方程的基础上，采用形式简单，气、液适应性好，通用性强的PR状态方程计算工质CO2的未知参数，根据实际染色情况选择合适的工况对系统进行有效能计算。

PR方程可以较为准确预测液体摩尔体积，其表达形式为

(6)

式中：P为压力，Pa；T为温度，K；Vm为摩尔体积，m3/mol；R为普适气体常数，8.314 J/(mol·K)；a，b为修正系数，具体计算式见文献[16]。

采用余函数法进行过程中焓差、熵差和有效能的计算[17]。以(T，V)为独立变量，采用PR状态方程得摩尔余焓(Hm,r)、摩尔余熵(Sm,r)，其表达式为：

(7)

(8)

式中：Hm,r为工质在状态(T，V)下的摩尔余焓，J/mol；Sm,r为工质在状态(T，V)下的摩尔余熵，J/(mol·K)。

过程中摩尔焓差(ΔHm,1-2)、摩尔熵差(ΔSm,1-2)计算式可表示为：

(9)

(10)

式中：ΔHm,1-2为工质由状态1(P1，T1)变化至状态 2(P2，T2)过程中的摩尔焓变量，J/mol；ΔSm,1-2为工质由状态1(P1，T1)变化至状态2(P2，T2)过程中的摩尔熵变量，J/(mol·K)；Hm,r1、Hm,r2分别为工质在状态1、2的摩尔余焓，J/mol；Sm,r1、Sm,r2分别为工质在状态1、2的摩尔余熵，J/(mol·K)；Cp为理想气体状态CO2摩尔热容，J/(mol·K)。

过程中单位质量有效能变化量(Δe1-2)表达式为

(11)

式中：Δe1-2为工质由状态1(P1，T1)变化至状态2(P2，T2)过程中的单位质量有效能变化量，kJ/kg；e1、e2分别为工质在状态1、2时的单位质量有效能，kJ/kg ；M为CO2摩尔质量，g/mol。

1.2.3计算工况及结果

超临界CO2无水染色系统有效能损失计算条件如下：染色压力为20、22 MPa；染色温度为373.15、393.15 K；节流分离压力为5 MPa；冷凝温度为273.15 K；环境温度为293.15 K。

染色过程中CO2质量流量为10.38 g/s；增压单元输入功率为1 500 W；加热/染色单元输入功率为3 500 W；制冷单元输入功率为3 000 W。

利用有效能平衡式编制计算程序，分别计算染色系统在如下所述4种条件下的有效能损失，即(20 MPa, 373.15 K)、(20 MPa, 393.15 K)、(22 MPa, 373.15 K)、(22 MPa, 393.15 K)4种工艺条件。计算结果如表1所示。

表1 染色系统在不同工艺条件下有效能计算结果Tab.1 Results of system available energy efficiency at different condition

由表1可看出，超临界CO2无水染色系统主要存在以下有效能损失：1)增压单元不可逆有效能损失，在4种工艺条件下分别占输入有效能的9.05%、9.05%、8.36%、8.36%；2)加热/染色单元中，电能转变为热能引起的能量质量降级和导热油与CO2存在换热温差引起的有效能损失在4种工艺条件下分别占输入有效能的38.19%、36.37%、38.73%、37.19%；3)节流/分离单元因节流不可逆过程造成的有效能损失在4种工艺条件下分别占输入有效能的6.51%、7.69%、6.81%、7.96%；4)制冷单元中制冷机组的有效能损失和冷凝器中传热温差引起的有效能损失，在4种工艺条件下分别占输入有效能的28.74%、28.41%、28.90%、28.51%；5)4种工艺条件下系统有效能效率分别为17.51%、18.18%、17.20%、17.98%。

对比表1中的计算结果可看出：1)系统有效能损失集中在加热/染色单元和制冷单元，二者有效能损失总和占输入有效能的60%以上，是系统节能改进的重点部位；2)相同压力条件(20 MPa、22 MPa)下，系统收益有效能在工艺温度393.15 K时比373.15 K分别高出0.67%、0.78%；3)相同温度条件(373.15 K、393.15 K)下，系统收益有效能在工艺压力20 MPa时比22 MPa时分别高出0.31%、0.2%。

因此，要明显改善系统的有效能利用情况，加热/染色单元和制冷单元的节能降耗是关键。对于加热/染色单元，电能转化为热能造成能量质量降级的有效能损失占绝大部分。采用能量品质较低的热能直接供热，减小换热温差等措施可减少加热过程中有效能损失，但同时也导致管路增加，换热器体积增大等问题。对于制冷单元，制冷机组的有效能损失相对较大。选用高效制冷设备，增大冷凝器面积等措施减少制冷单元有效能损失；但制冷设备的性能受限于制冷机组的制造水平及制冷循环方式，冷凝器换热面积受限于安装尺寸，因此，调整现有设备工艺参数和改进染色循环方式是降低系统能耗的 2条可选途径，下文将分析染色工艺参数对加热/染色单元和制冷单元有效能效率的影响。

2 工艺参数对单元有效能效率的影响

2.1 加热/染色单元有效能效率的分析

加热/染色单元是通过电加热器加热导热油，高温导热油与CO2换热，通过控制导热油温度调节工艺要求温度。加热/染色单元的有效能效率(ηq)定义为

(12)

计算加热/染色单元在下述条件的有效能效率，即：工质入口温度保持在293.15 K；染色工艺压力分别为20、22、24 MPa；染色工艺温度分别为353.15、373.15、393.15 K。图7示出不同染色压力条件下工艺温度对加热/染色单元有效能效率的影响。

图7 不同染色压力条件下工艺温度对 加热/染色单元有效能效率的影响Fig.7 Effect of temperature on available energy efficiency of heating/dyeing unit under different dyeing pressures

由图7可看出：染色压力一定时，随着工艺温度升高，单元有效能效率明显增加；相同工艺温度条件下，压力升高，单元有效能效率降低。计算显示，在染色压力分别为20、22、24 MPa的条件下，随着染色工艺温度由353.15 K升高到393.15 K，加热/染色单元有效能效率分别由8.7%、7.8%、7.1%提高至16.0%、15.0%、14.1%。热力学第二定律指出，系统有效能受温度影响较大，系统温度高于环境温度时，温度越高，其所具有的有效能越大。因此，温度升高，加热过程吸收的有效能增多，单元有效能效率增加。从热力学角度考虑，适当降低染色压力，提高染色温度，可提高加热过程有效能效率。

2.2 制冷单元有效能效率的分析

制冷单元是通过制冷机组冷却制冷剂(乙二醇)，由低温乙二醇制冷节流分离后的CO2气体，气态CO2冷却至饱和温度下成液态，其饱和温度主要受节流分离后气体压力的影响。制冷单元有效能效率(ηq0)计算式为

(13)

计算制冷单元在下述条件的有效能效率，即：节流压力分别为4、4.5、5、5.5、6 MPa；节流分离后气体温度(即冷凝器入口温度)分别为293.15、295.15、297.15 K。图8示出不同冷凝温度条件下节流压力对制冷单元有效能效率的影响。

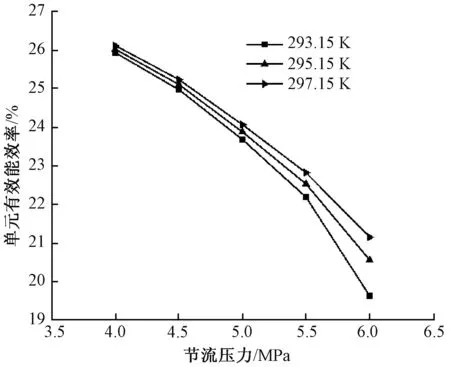
图8 不同冷凝温度条件下节流压力对 制冷单元有效能效率的影响Fig.8 Effect of throttling pressure on available energy efficiency of refrigeration unit at different condensation temperatures

由图8可看出：相同冷凝温度条件下，节流分离压力升高，制冷单元有效能效率明显下降；相同节流压力条件下，制冷单元有效能效率随温度变化并不明显。计算显示，在冷凝温度分别为293.15、295.15、297.15 K的条件下，随着节流分离压力由 6 MPa降至4 MPa，单元有效能效率分别由19.6%、20.6%、21.2%升高至25.9%、26.0%、26.1%。因CO2饱和温度受饱和压力影响较大，压力下降时，饱和温度降低，故相同冷凝温度条件下，低压时冷凝器制冷CO2温度更低，制冷单元有效能效率增加。因此，适当降低工艺节流压力，制冷单元有效能效率增加，但节流压力的降低，会产生节流/分离单元有效能损失增加和增压单元负荷增加的问题。选择合适的工艺节流压力，以减少系统有效能损失是需要研究的另一个问题。

3 结 论

本文运用有效能分析法对超临界CO2无水染色系统的能耗状况进行了计算分析，建立了系统各单元的有效能平衡方程，采用PR方程计算工质未知参数，采用余函数法计算系统有效能损失，重点分析了染色温度对加热/染色单元和节流压力对制冷单元有效能效率的影响。通过计算分析得到如下结论。

1) 染色系统的加热/染色单元与制冷单元有效能损失量总和占系统输入有效能的60%以上，是系统节能改进的重点部位。

2) 染色压力在20～24 MPa的范围内，染色温度由353.15 K升至393.15 K时，加热/染色单元有效能效率由最低的7.1%提高到16.0%；冷凝温度在293.15～297.15 K的范围内，节流压力由6 MPa降至4 MPa时，制冷单元有效能效率由最低的19.6%提高至26.1%。

3) 从热力学角度考虑，适当降低染色压力，提高染色温度，将提高加热过程有效能效率。适当降低节流分离压力，将提高制冷单元有效能效率，但同时会导致节流/分离单元有效能损失增加和增压单元工作负荷的增加，最佳工艺节流分离压力需要进一步研究。