极限思想在高等数学中的应用

徐泰燕

(武昌工学院，湖北 武汉 430065)

高等数学的学习离不开函数的极限思想，尤其在函数的连续性、微积分、无穷级数等章节内容体现得更为淋漓尽致。下面就高等数学不同知识板块极限思想的运用进行系列讨论，且讨论仅就一元函数为例进行讨论，对于多元函数类比推导即可。

一、函数的连续性定义及连续性判断

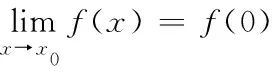
例1判断函数f(x)=|x|在x=0处的连续性.

二、导数的定义及函数的可导性判断

例2判断函数f(x)=|x|在x=0处的可导性.

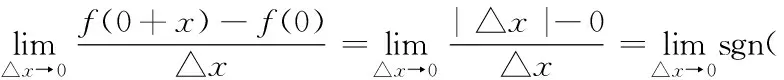
三、黎曼积分定义及可积性判断

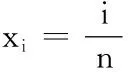
四、无穷级数的敛散性判断

类似于无穷级数敛散性判断需要判断{sn}是否收敛，函数能否展开成泰勒级数也要依赖于对应泰勒公式的余项当n→∞时是否极限为零。内容相似，篇幅有限，不再列举赘述。

极限思想源远流长，它使人们的认识从有限上升到无限、从近似上升到精确、从量变上升到质变，渗透在整个高等数学学科知识中，使各知识模块之间发生千丝万缕的联系，学好极限，熟练掌握极限思想，不但能帮助学生串联整个知识体系，学好高等数学这门专业基础课，同时对于发展学生的数学思维能力也大有裨益。