基于广义粒子群优化模型的工艺规划方法研究
文笑雨, 罗国富, 李 浩, 肖艳秋, 乔东平, 李晓科
(郑州轻工业学院 河南省机械装备智能制造重点实验室,河南 郑州 450002)
0 引言
工艺规划的输入是产品的设计数据,输出为产品具体的制造信息,它对制造系统的性能有着重要的影响[1].由于柔性制造系统和数控加工中心的广泛应用,许多零件在生产加工时,存在大量的柔性工艺可供选择,同时,每道加工工序还有众多可选的加工资源,这使得工艺规划问题成为一个典型的NP(non-deterministic polynomial)-Complete 问题,传统的方法很难有效地解决该问题[1].
近年来,越来越多的智能优化算法被应用于解决现代制造系统中的工艺规划问题,如粒子群优化(particle swarm optimization, PSO)[1]、殖民竞争算法[2]、蚁群算法[3-4]、蝙蝠算法[5]、遗传算法[6](GA)、禁忌搜索[6](TS)和模拟退火算法[6](SA)等.在上述方法中,PSO算法是一种基于群体智能理论的优化算法.传统的PSO适合于处理连续优化问题,随着研究的深入,许多学者对传统的PSO进行改进,将其广泛应用于诸多复杂的组合优化问题中,如旅行商问题[7]、作业车间调度问题等[8-9].其中,高海兵等[7]提出的广义粒子群优化(general PSO, GPSO)模型建立了一种将PSO应用于组合优化问题的通用思路,在应用GPSO模型求解工艺规划问题时,值得进一步去探索更加有效的粒子全局更新策略和局部搜索策略.
笔者在广义粒子群优化模型基础上,结合工艺规划问题的特性,设计了基于个体极值库和种群极值库的粒子全局更新策略,引入变邻域搜索算法作为粒子的局部搜索策略,提出了求解工艺规划问题的改进GPSO(improved GPSO, IGPSO)算法,并使用已有工艺规划文献中的6个典型零件对提出的算法进行了测试,验证了提出算法的有效性.
1 工艺规划问题描述
本文研究的工艺规划问题可被描述为:某待加工零件具有多种加工特征,每种加工特征具有不同的可选加工工艺,每一种可选加工工艺可能包含多道加工工序,每道加工工序可以在若干台可选机器上进行加工,被加工零件的不同特征之间具有一定的次序约束关系.工艺规划的目的是在已有加工资源和加工约束的情况下,确定被加工零件的工艺路线,从而使得某项指标达到最优.在本文中,选择待加工零件的加工时间作为优化目标,并进行如下假设:
(1)同一零件的不同工序不能被同时加工;
(2)在0时刻,所有的机器都是可用的;
(3)每道工序的加工时间被定义为常数;
(4)一个零件在一台机器上加工完成之后,它被立刻传送至工艺路线中的下一台机器,零件在不同机器之间的传输时间被定义为常数;
(5)机器加工每道工序的准备时间和工序加工顺序是相互独立的,并被包含在每道工序的加工时间中.
为了形象地描述所研究的问题,针对某待加工零件详细说明如何进行工艺规划操作.表1给出了某零件的加工工艺信息表.
该零件包含有9个加工特征,有5台机器可供选择对零件不同的工序进行加工.确定该零件的工艺路线需要经过三个步骤:第一,确定不同加工特征的顺序,该顺序必须满足不同特征之间的次序约束关系;第二,确定每种加工特征具体的加工工艺;第三,对具有可选加工机器的工序确定具体的加工机器.
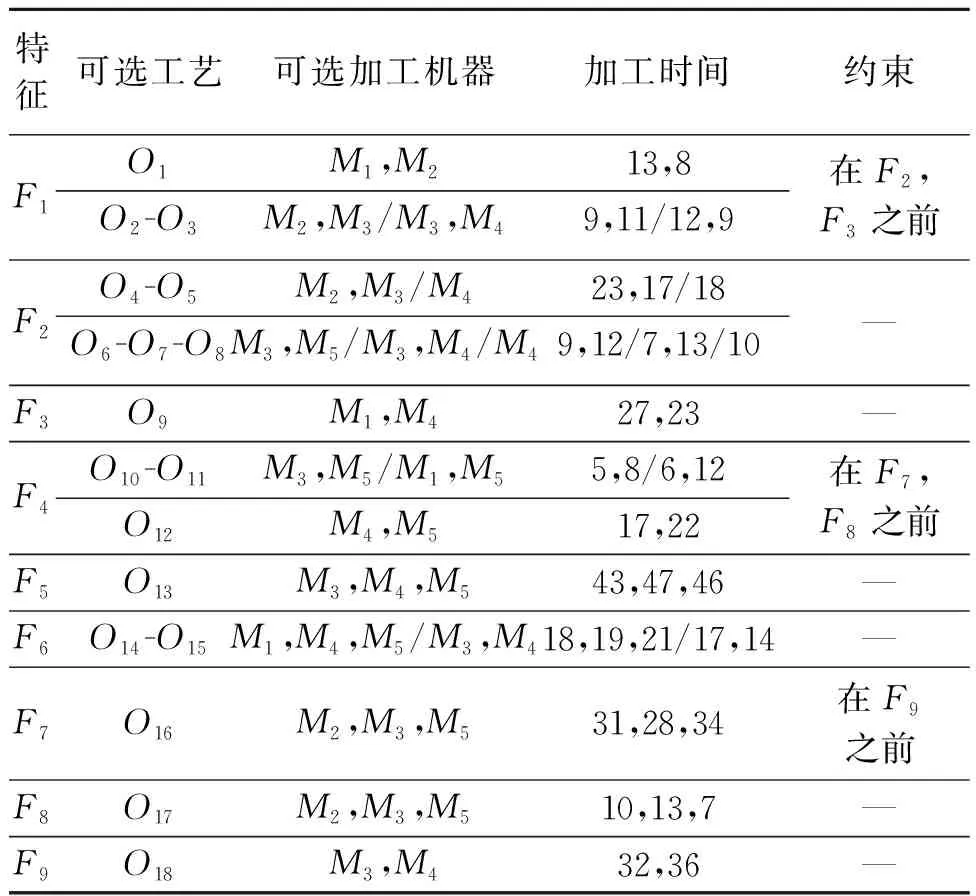
表1 某零件的加工工艺信息表Tab.1 Machining process information of a part
当该零件的工艺路线确定之后,可以计算出该零件的总加工时间.基于上述问题描述,本文研究的工艺规划问题优化目标为零件的总加工时间(processing time,PT)最短,具体计算方法如下所示:
MinPT=OT+TT,
(1)
式中:OT为零件的工序加工时间;TT为零件在不同机器之间的传输时间.
(2)
式中:OTi为工艺路线中第i道工序的加工时间;n为零件的工艺路线中包含的工序数目.
(3)
如果零件相邻的两道工序在不同的机器上进行加工,则需要一定的机器传输时间,TTMi,Mi+1为从工艺路线中第i道工序的加工机器Mi转换到第i+1道工序的加工机器Mi+1所需要的传输时间.
(4)
当相邻两道工序在相同的机器上加工时,式(4)为0;当相邻两道工序在不同的机器上加工时,式(4)为1.
2 IGPSO求解工艺规划问题
2.1 广义粒子群优化算法模型
高海兵等[7]通过对传统PSO核心优化机理的分析,忽略粒子的具体更新策略,总结出了GPSO模型,其基本流程如图1所示.笔者在GPSO模型下设计求解工艺规划问题的IGPSO算法,接下来将分别介绍基于IGPSO算法的工艺规划方法主要组成部分以及算法流程.
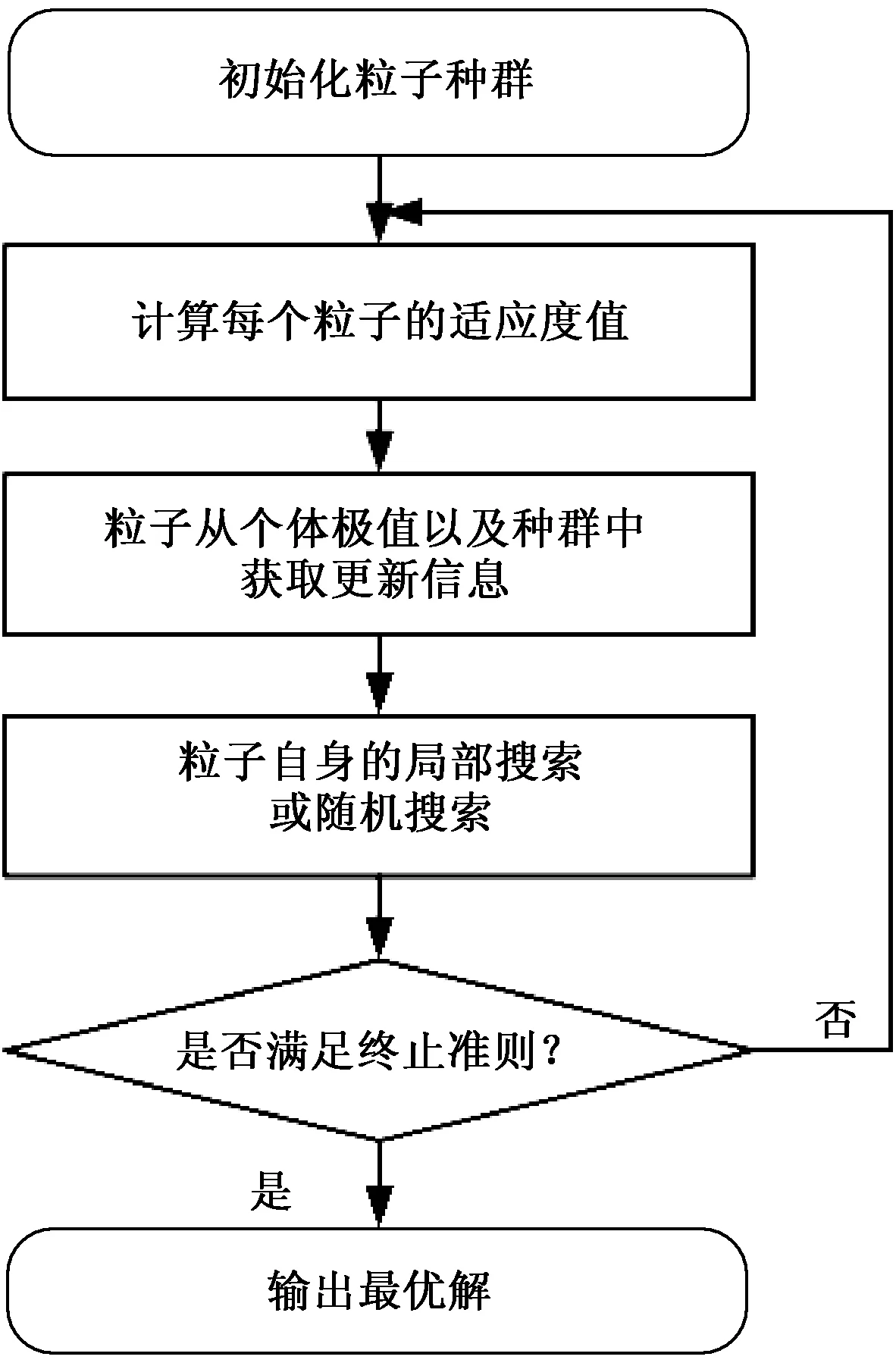
图1 广义粒子群优化模型[7]Fig.1 General particle swarm optimization model
2.2 粒子的编码与解码
每一个粒子代表零件的一条具体的工艺路线,笔者采用文献[1]中的编码与解码方法对粒子进行编码与解码操作.每一个粒子包含三段长度不同的序列:第一段为特征序列;第二段为可选工艺序列,这两段序列的长度均等于零件的总特征数;第三段为可选机器序列,该序列的长度等于零件的总工序数.以表1中的零件为例,一种可行的粒子编码方案如图2所示.特征序列代表的含义为该零件特征加工顺序为:F4-F1-F8-F7-F5-F9-F2-F3-F6.
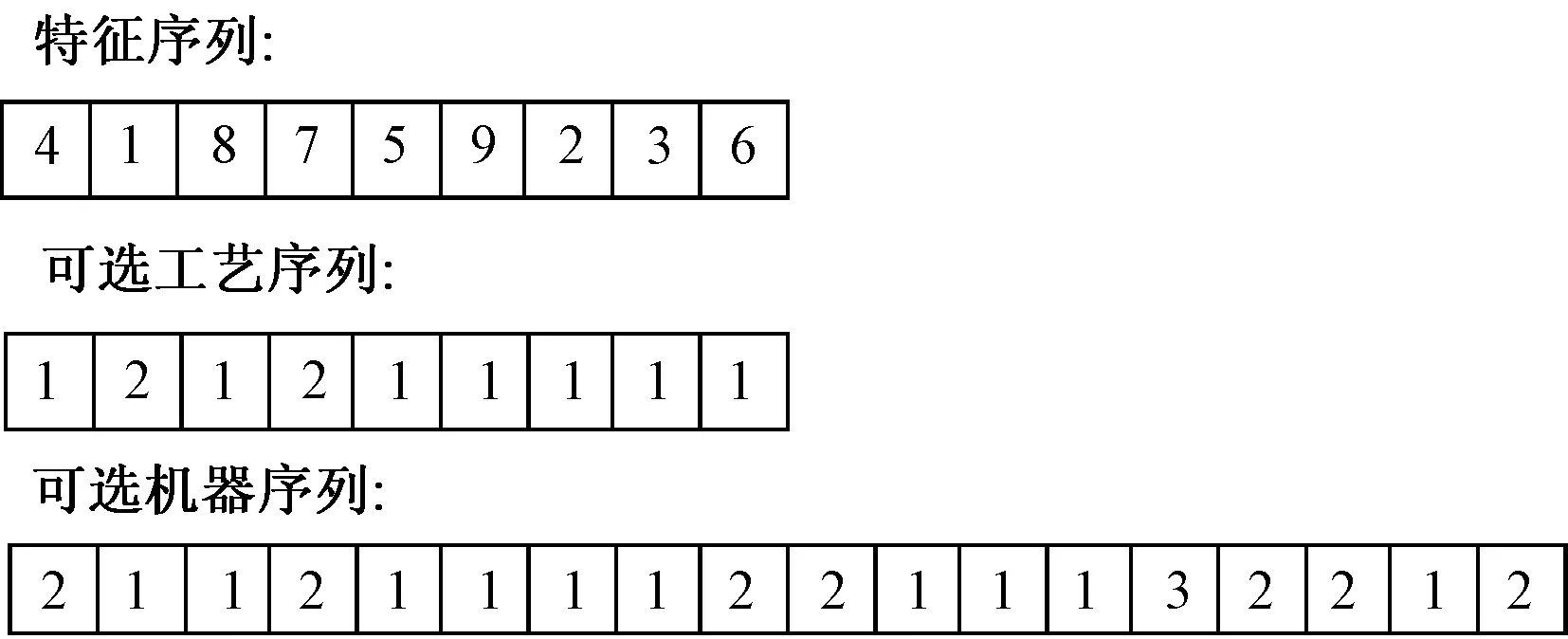
图2 粒子对应的编码方案Fig.2 Corresponding encoding scheme for a particle
可选工艺序列的第i个位置的数字k,代表了第i个特征选择第k种可选加工工艺进行加工,如图2中可选工艺序列中第二个位置为2,则代表特征2从它的可选工艺集{O4-O5,O6-O7-O8}中选择第2种加工工艺,即O6-O7-O8进行加工.可选机器序列中第i个位置的数字k,代表了零件的第i道工序从可选加工机器集当中选择第k个加工机器,如图2中可选机器序列第1个位置为2,则代表工序1从它的可选加工机器集{M1,M2}中选择了第二个机器,即M2进行加工.
该编码方案经解码后代表所确定的零件工艺路线为:O12(M4)-O1(M2)-O17(M2)-O16(M3)-O13(M3)-O18(M3)-O6(M3)-O7(M3)-O8(M4)-O9(M4)-O14(M4)-O15(M4).
2.3 初始化粒子种群
粒子种群中的每一个粒子代表零件的一种工艺规划方案.按照编码操作,每一个粒子包含三段序列,均采用随机初始化的方法进行初始化操作.每个粒子随机初始化编码之后,利用文献[10]的约束调整方法调整编码方案,然后使用解码操作对其进行解码,获得具体该粒子所代表的零件工艺路线;根据具体的工艺路线,计算该工艺路线下零件的总加工时间,将染色体所对应工艺路线的总加工时间直接作为适应度值.
2.4 粒子的全局更新策略
IGPSO中粒子的全局更新采用文献[1]中的交叉操作来实现.为了避免进行无效的交叉操作,设定个体极值库,保存粒子在搜索过程中发现的最好的若干个解(一般取2~3个)[11].为了避免算法过早收敛,设定种群极值库保存整个搜索过程中发现的最好的若干个解(一般取整个种群的20%~30%).当前粒子通过与个体极值库和种群极值库中不同的粒子进行交叉操作,获取更新信息.
2.5 粒子的局部搜索策略
采用变邻域搜索算法作为粒子的局部搜索策略,详细步骤如下:
步骤1根据粒子的编码方案,定义3种邻域结构N1、N2、N3.其中,N1为交换操作,即随机选择粒子中特征序列上不同的两个位置,将这两个位置上的数值进行交换;N2为插入操作,随机选择粒子中特征序列的一个位置,将这个位置上的数值插入到该序列的任意其他位置之前;N3为变异操作,随机选择粒子中可选工艺序列、可选加工机器序列中的一个位置,根据其可选加工资源情况,选择另外一种加工资源.设定外循环最大迭代次数MaxIterOut,内循环最大迭代次数MaxIterIn.令i=0,l=0.i代表当前内循环次数,l代表当前外循环次数.
步骤2随机挑选一种邻域结构,产生当前粒子Pcurr的邻域解P1.
步骤3当i大于MaxIterOut时,输出Pcurr;否则,顺序执行.
步骤4当l大于MaxIterIn时,令i=i+1, 若P1的适应度值小于Pcurr,则令Pcurr=P1,跳转到步骤3;当l小于或等于MaxIterIn时,顺序执行.
步骤5令k=1,k代表当前使用的邻域结构编号.
步骤6根据Nk随机产生P1邻域解P2.如果P2的适应度值小于P1,则令P1=P2,k=1,跳转到步骤6(继续按照当前邻域结构进行搜索);如果P2的适应度值大于P1,则令k=k+1,如果k小于等于3,跳转到步骤6(继续搜索下一个邻域).如果k大于3,顺序执行.
步骤7令l=l+1, 跳转到步骤4.
2.6 IGPSO求解工艺规划的总流程
步骤1设定算法参数:种群规模PopSize;种群极值库规模GlobSize;个体极值库规模SelfSize;最大迭代次数MaxGen;粒子全局搜索的概率GlobProb;粒子局部搜索的概率LocalProb;变邻域搜索中外循环最大迭代次数MaxIterOut;内循环最大迭代次数MaxIterIn.
步骤2随机初始化种群和个体极值库,挑选种群中适应度值最好的20%个粒子存入种群极值库.
步骤3依据粒子全局搜索的概率,依次对种群中的粒子进行全局搜索,更新个体极值库和种群极值库.
步骤4依据粒子局部搜索的概率,依次对种群中的粒子进行局部搜索,更新个体极值库和种群极值库.
步骤5如果循环达到最大迭代次数,则输出种群极值库中最好的个体作为优化结果;如果循环没有达到最大迭代次数,则跳转到步骤3.
3 计算结果及分析
3.1 算例及计算结果
上述提出的IGPSO算法用C++语言编程实现.本文的测试实例包含对6个不同的零件进行工艺规划,以验证提出算法的有效性.零件1包含14个加工特征20道可选加工工序;零件2包含15个加工特征16 道可选加工工序;零件3包含11个加工特征14道可选加工工序;零件4包含13个加工特征13道可选加工工序;零件5包含7个加工特征9道可选加工工序;零件6包含14个加工特征18道可选加工工序.零件图和具体的加工信息表见文献[1].笔者假定在车间中有5台机器用于零件加工,零件在不同机器之间的传输时间见文献[1].算法参数设置如下:种群规模设定为200, 种群极值库规模设定为40,个体极值库规模设定为3,最大迭代次数设定为100,粒子全局搜索的概率设定为0.8,粒子局部搜索的概率设定为0.3,变邻域搜索中外循环最大迭代次数设定为20,内循环最大迭代次数设定为20.
使用笔者提出的IGPSO算法针对6个零件独立计算20次,统计了20次运行中获得零件工艺路线对应加工时间的最好值、平均值以及平均收敛代数,具体计算结果以及与其他算法的对比如表2所示,其中,SA、GA和MPSO(改进PSO)算法的计算结果均来自文献[1].笔者提出的IGPSO获得的最优工艺路线如表3所示.
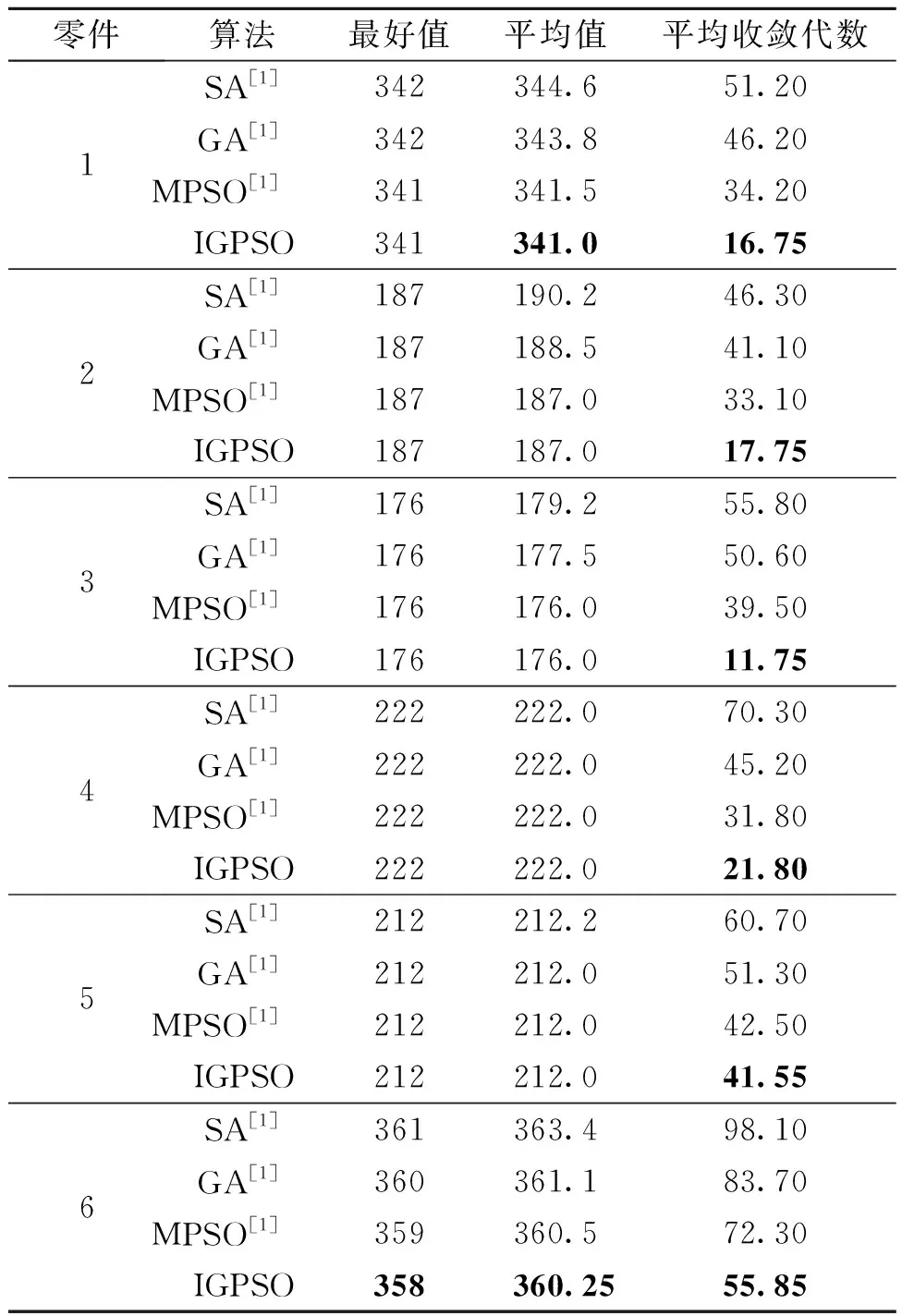
表2 IGPSO计算结果及与其他算法的对比Tab.2 Results obtained by IGPSO and the comparisons with other algorithms

表3 IGPSO获得的最优工艺路线Tab.3 Optimal process plans obtained by IGPSO
从表2可以看出,针对零件1~零件5,使用本文提出的IGPSO算法在20次独立运行中每次均都能够找到最优解.在最好值上,针对零件1,IGPSO算法的计算结果优于SA和GA,与MPSO的计算结果相同.针对零件2、零件3、零件4和零件5,4种算法在最好值上的计算结果相同,但是与SA、GA和MPSO算法相比,笔者提出的IGPSO算法的平均收敛代数较少.针对零件6,笔者提出的IGPSO在最好值、平均值和平均收敛代数上均优于其他3种算法.
3.2 计算结果分析
整体来说,4种算法在本文的测试实例中显示的性能从优到劣顺序为:IGPSO>MPSO>GA>SA.虽然在零件1~零件5的测试中,SA算法获得了最优解,但是与其他3种算法相比,它所获得的平均值比较大,平均收敛代数也比较大.这是因为SA是一种局部搜索算法,计算结果比较依赖于初始解.相比SA,全局搜索能力比较好的GA获得的计算结果更加稳定,平均收敛次数低于SA,在零件6的测试中,获取了比SA更好的解.在零件1~零件5的测试中,MPSO获得的最好值与GA相同,平均值小于或等于GA获得的结果,平均收敛代数均优于GA.在零件6的测试中,MPSO获得了更小的最优解.这是因为,与GA的并行全局搜索策略相比,MPSO在粒子的全局更新策略上有所不同,当前粒子通过与个体极值和种群极值库中的粒子进行交叉操作,迅速向解空间中较好的区域进行移动,因此,MPSO平均收敛代数小于GA. 在零件1~零件5的测试中,IGPSO取得了与MPSO相同的最好值,在平均值上略优于MPSO获得的计算结果,平均收敛次数优于MPSO.在对零件6的测试中,IGPSO获得了新的最优解,平均值与平均收敛次数也优于MPSO获得的结果.与MPSO相比,笔者提出的IGPSO在算法的局部搜索策略上引入了变邻域搜索算法,增强了粒子的局部搜索能力,因此算法的平均收敛次数较少,且在零件6的测试中发现了新的最优解.通过不同测试实例的计算结果可以证明,笔者提出的算法IGPSO在求解工艺规划问题上具有一定优势.
4 结束语
笔者设计了一种IGPSO算法求解柔性工艺规划问题,计算结果显示,与其他算法相比,笔者提出的IGPSO算法在求解工艺规划问题时具有更高的求解效率和更好的稳定性.
在今后的研究工作中,可以从工艺规划问题建模和求解算法设计两个方向进一步深入研究.在工艺规划问题建模上,考虑进一步研究面向绿色制造模式的工艺规划问题建模方法;在求解算法设计上,笔者设计的IGPSO算法,是通过改变GPSO算法的操作算子,对算法的收敛和发散进行控制.近年来,涌现出了一些新型的群体智能优化算法,能够将数据挖掘的思想融入群体智能优化算法设计中,如头脑风暴优化算法[12],为算法的设计提供了一种新思路.因此,考虑在今后的研究工作中,对基于头脑风暴算法的柔性工艺规划方法进行进一步的研究.

