幅度及多普勒信息辅助的多目标跟踪算法

彭华甫，黄高明，田威，邱昊

1. 海军工程大学 电子工程学院，武汉 430033 2. 中国人民解放军92773部队，温州 325807

多目标跟踪(Multi-Target Tracking, MTT)是未来信息化战争的关键技术之一，其目的是利用传感器观测数据估计目标数目及状态[1]，在战场监视、防空反导等领域应用广泛。

经典的多目标跟踪算法基于数据关联的思想，将跟踪过程分为数据关联和状态估计两步。随着目标及杂波数目的增加，数据关联的复杂度呈指数增长。基于随机有限集(Random Finite Set, RFS)[2]的多目标跟踪技术，能有效避免复杂的数据关联过程，成为目前多目标跟踪领域的研究热点。概率假设密度(Probability Hypothesis Density, PHD)滤波器是泊松分布下多目标后验概率密度在Kullback-Lerbler准则下的最优近似[3]，证明了RFS算法的可行性，但算法稳定性差；势概率假设密度(Cardinality Probability Hypothesis Density, CPHD)滤波器[4]在其基础上引入目标数目的二阶信息，以增大计算量为代价提高了跟踪稳定性；由于PHD及CPHD采用序贯蒙特卡罗(Sequential Monte Carlo, SMC)实现时，状态提取精度取决于聚类算法的稳定性，多目标多伯努利(Multi-target Multi-Bernoulli, MeMBer)滤波器[2]对多目标后验概率密度函数进行数值近似，可直接估计目标数目及状态，避免了复杂而不稳定的聚类过程。然而，当杂波数量增大时，这些滤波器跟踪性能严重衰减。为提高杂波环境下的适应能力，利用幅度信息及多普勒信息可提高目标跟踪性能[5-6]。文献[7-9]分别将幅度信息引入到PHD、CPHD、MeMBer滤波器中，文献[10-12]分别将目标多普勒信息引入到高斯混合PHD(Gaussian Mixture PHD, GM-PHD)、CPHD滤波器，均有效抑制了杂波影响。但由于PHD、CPHD、MeMBer滤波器理论的局限性，这些改进算法在高杂波环境下跟踪性能受限，且无法直接形成航迹。

近年来提出的δ广义标签多伯努利(δ-Generalized Labeled Multi-Bernoulli,δ-GLMB)滤波器[13]，是多目标跟踪的一种闭式解决方案，被证明是贝叶斯最优估计[14]，具有更强的杂波抑制能力、更高的估计精度且可直接估计目标航迹，在机动目标跟踪[15]、衍生目标跟踪[16]、多传感器信息融合[17]等领域受到了广泛关注。然而，其在实现中面临计算复杂度大、强杂波和密集目标环境下“组合爆炸”的问题。对此，文献[13]采用K最短路径及排列分配算法进行假设裁剪，文献[18] 结合量测分组大幅降低了计算量，文献[19]结合吉布斯采样裁剪及预测、更新合并提出了一种快速实现算法。

现有多目标跟踪方面的研究大多仅利用目标的单一信息，随着战场环境的日趋复杂，综合利用多种信息可从多个维度对算法进行优化，提高适应能力，是未来的一个发展趋势。目前，基于δ-GLMB滤波器的研究还未考虑将幅度信息或多普勒信息引入其中以提高跟踪性能，且现有算法虽进行了各种简化处理，但强杂波环境下计算量仍较大。对此，本文通过联合幅度及多普勒信息，基于δ-GLMB滤波器框架，提出了一种综合利用多辅助信息的融合算法。通过引入幅度及多普勒信息对目标量测状态进行扩展，利用幅度、多普勒及位置的联合量测似然函数代替单一的位置量测似然函数，增强目标与杂波的区分度，推导了新的量测更新方程，提出了幅度及多普勒信息辅助的δ-GLMB滤波器(ADI-δ-GLMB)。仿真实验表明，本文所提算法估计精度更高、抗干扰能力更强，且有效降低了高杂波环境下的计算量。

1 目标建模

1.1 状态建模

假设二维运动场景中，k-1时刻有Nk-1个目标，其状态可表示为

i=1,2,…,Nk-1

(1)

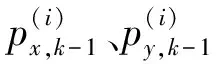
(2)

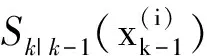
1.2 量测建模

引入幅度及多普勒量测信息后，k时刻目标量测可表示为

(3)

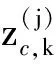
Zk=Θ(Xk)∪Kk

(4)

式中：Kk为虚警杂波量测集合；Θ(Xk)为检测到的目标量测集合，检测概率pD,k<1。

假设传感器位于坐标原点，目标位置量测方程可表示为

zc,k=Hc,kxk+wk

(5)

式中：

其中：wk和Rc,k为位置量测噪声矩阵和噪声协方差矩阵。则目标位置量测似然函数为

g(zc,k|xk)=N(zc,k;Hc,kxk,Rc,k)

(6)

目标多普勒量测方程为

zd,k=hk(xk)+nk

(7)

式中：

其中：nk和Rd,k分别为多普勒量测噪声和噪声方差。

则目标多普勒量测似然函数为

g(zd,k|xk)=N(zd,k;hk(xk),Rd,k)

(8)

雷达系统中，回波信号幅度与回波平均信噪比(Signal-to-Noise Ratio，SNR)S有关，通常可将其建模为瑞利分布，目标幅度及杂波幅度的概率密度分别表示为[8]

(9)

(10)

假设检测门限为τ，则经过门限检测后，目标及杂波幅度的概率密度可表示为

(11)

(12)

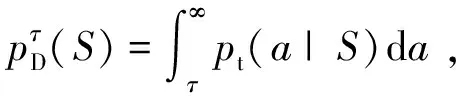
实际中，由于大气、云层及目标雷达散射截面积(Radar-Cross Section，RCS)等因素的影响，目标回波SNR时变。假设回波SNR在[dB1,dB2]内均匀分布，对应S的取值范围为[S1,S2]。则目标幅度似然函数可简化表示为[8]

g(za|xk)=g(za)=

(13)

由式(5)和式(7)可以看出，目标位置量测、多普勒量测仅与目标状态有关，回波幅度仅与回波信号SNR有关，可假设位置、多普勒及幅度量测间相互独立。结合式(6)、式(8)和式(13)，位置、幅度及多普勒信息的联合量测似然函数可表示为

g(zk|xk)=g{[zc,kzd,kza,k]|xk}=

g(zc,k|xk)g(zd,k|xk)g(za,k|xk)=

(14)

假设杂波量测的坐标、多普勒及幅度相互独立，则联合杂波密度可表示为

c(zk)=c(zc,k,zd,k,za,k)=

c(zc,k)c(zd,k)c(za,k)

(15)

式中：c(zc,k)为空间位置杂波密度函数；c(zd,k)为多普勒杂波密度函数；c(za,k)为杂波幅度似然函数[8]，其表达式为

(16)

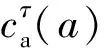
2 ADI-δ-GLMB滤波器

目标状态可由标签RFS表示为

X={(x,l)i}i=1,2,…,N

(17)

式中：x∈Xs为目标状态向量；l∈Ls为其对应的标签；X⊆Xs×Ls，Xs为目标状态空间，Ls为离散的标签空间。

假设k时刻，多目标后验密度πk-1(X)服从δ-GLMB分布[13]

πk-1(X)=Δ(X)·

δI(L(X))(pk-1(·;ε))X]

(18)

式中：

I∈F(Lk-1)为标签集合；Lk-1为k-1时刻的离散标签集；F(L)为L的所有有限子集空间；L(X)为Xs×Ls→Ls的映射，有L((x,l))=l；ε∈Θ为历史关联；Θ为关联空间；(I,ε)为关联假设；ω(I,ε)为其相应权值；p(·;ε)为单目标概率分布；|·|为取势计算；hX=∏x∈Xh(x)。

假设k时刻新生目标也服从δ-GLMB分布[13]：

πB,k(X)=Δ(X)·

(19)

式中：LB,k为新生目标标签空间，Lk∩LB,k=∅；pB,k(·)为新生目标概率分布。

2.1 预测

由于引入的幅度量测及多普勒量测信息并未影响目标的状态转移，因此，k时刻ADI-δ-GLMB滤波器的多目标预测分布πk|k-1(X)同标准的δ-GLMB滤波器，可表示为[13]

πk|k-1(X)=Δ(X)·

δI(L(X))(pk|k-1(·;ε))X]

(20)

式中：

2.2 更新

分析文献[13]中标准δ-GLMB滤波器更新方程可以发现：引入幅度及多普勒量测信息对目标量测进行扩展后，仅对公式中的目标量测似然函数及杂波密度产生了影响。因此，分别用式(14) 和式(15)所示的联合量测似然函数及联合杂波密度代替原公式中的位置量测似然函数及杂波密度，则可得k时刻ADI-δ-GLMB滤波器的多目标更新分布

πk(X|Zk)=Δ(X)·

(pk(·;ε,ζk|Zk))X]

(21)

式中:

其中：Lk=Lk|k-1；pD,k(·)为目标探测概率；对于k时刻预测假设(I,ε)，ζk为目标与量测的关联映射{l1,l2,…,l|I|}→{0,1,…,|Zk|}，当ζk(l)=0时，目标与空量测关联，即目标漏检；λ为杂波强度。

分析式(21)可以发现：当幅度信息无法获取或利用幅度信息无法对目标与杂波进行区分时，gk(za,k|·)/c(za,k)=1，ADI-δ-GLMB滤波器仅受多普勒信息约束，退化为多普勒信息辅助的δ-GLMB(DI-δ-GLMB)滤波器；当多普勒信息无法获取时，令gk(zd,k|·)/c(zd,k)=1，ADI-δ-GLMB滤波器退化为幅度信息辅助的δ-GLMB(AI-δ-GLMB)滤波器；当两者都失效时，则退化为δ-GLMB滤波器。

2.3 计算复杂度分析

在算法实现时，为有效降低计算量，本文采用文献[13]中的假设裁剪及文献[18]中的量测分组技术来简化计算。标准δ-GLMB滤波器仅利用位置量测信息，无法对真实目标与杂波进行区分，因此其更新步中的关联过程需要考虑所有航迹假设，计算复杂度为O(NM3)，其中：N为目标个数，M为量测个数[16]。强杂波环境下，量测数据中包含大量杂波(M≫N)，极限情况下量测分组失效，计算量成指数增长。而ADI-δ-GLMB滤波器综合利用位置、幅度、多普勒信息，可从多个维度提高目标与杂波的区分度，从而可去除部分杂波量测的影响，理想条件下当利用辅助信息能将目标与杂波量测完全区分时，可使得M≈N，因此计算复杂度为O(N4)，大幅降低了计算量；当辅助信息失效时，计算复杂度为O(NM3)。

3 仿真实验

假设有5个目标在二维观测区域[-1 000,1 000] m ×[-1 000,1 000] m内作协同转弯运动，目标运动状态如表1所示，多普勒速度限定在[-35,35] m/s范围内。

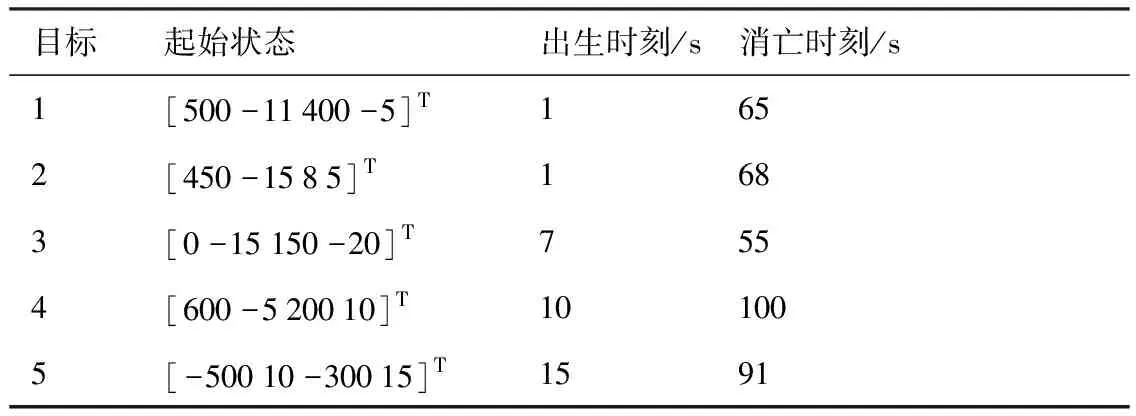
表1 目标运动状态Table 1 Dynamic states of targets

目标状态转移矩阵为

过程噪声协方差矩阵为

式中：σv=0.1 m/s为噪声标准差；Ts=1 s为传感器扫描间隔，扫描时间长度为100 s，目标存活概率pS=0.95。

图1为ADI-δ-GLMB算法单次实验结果，可以看出：强杂波下仍能对多目标进行有效跟踪。

为评估算法的性能，对标准δ-GLMB[13]及信息辅助的幅度信息δ广义标签多伯努利(Amplitude Informationδ-GLMB, AI-δ-GLMB)[8]、多普勒信息δ广义标签多伯努利(Doppler Informationδ-GLMB, DI-δ-GLMB)[10]、ADI-δ-GLMB算法进行比较。分别进行100次蒙特卡罗实验，并采用最优子模式分配(Optimal Sub-Pattern Assignment，OSPA)[20]作为评估因子，参数设置为：c=50、p=1。

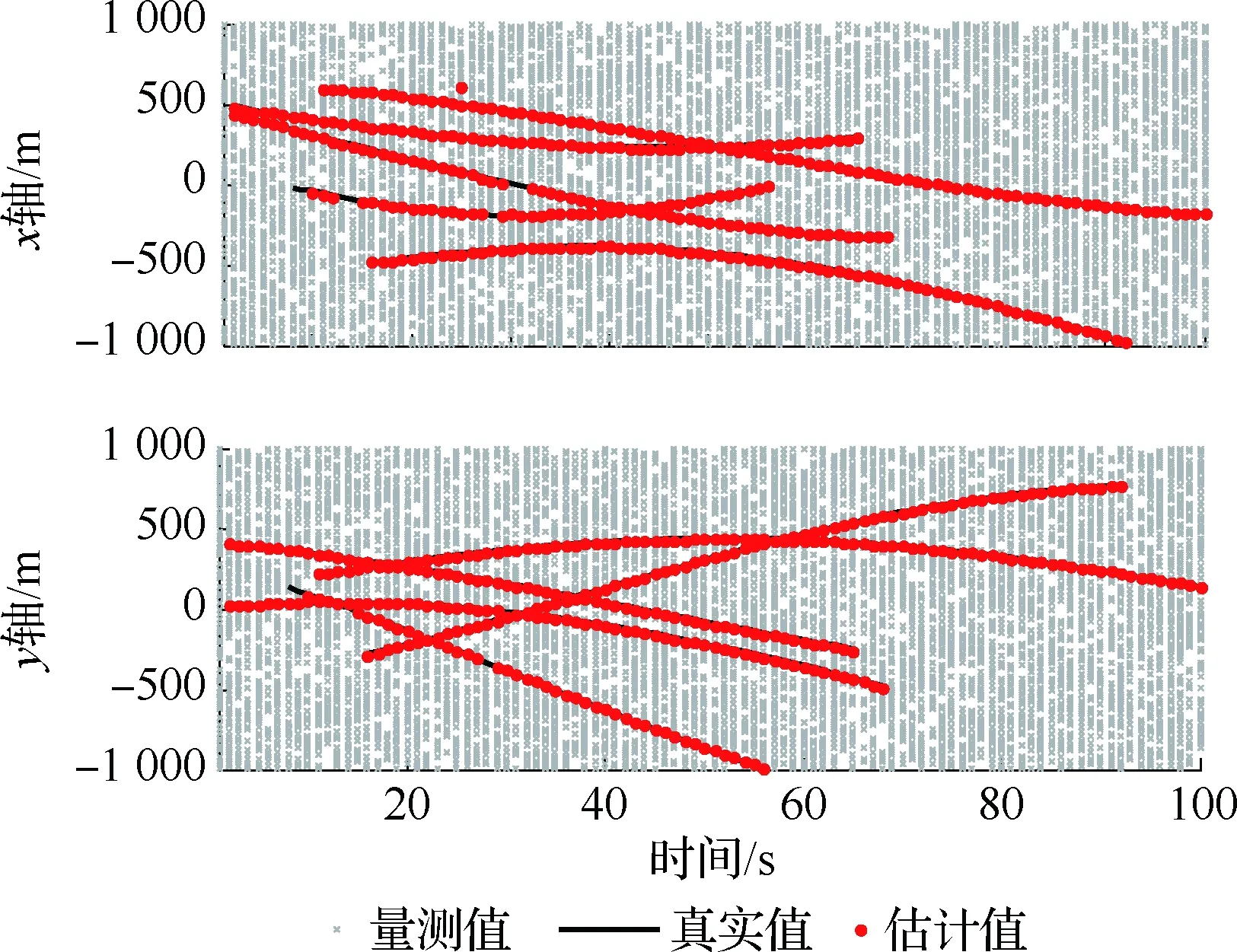
图1 目标真实航迹和状态估计Fig.1 True trajectories and state estimates of targets

图2为不同算法的势估计结果。可以看出：当杂波密集分布时，标准δ-GLMB会出现目标数目过估，且估计标准差较大；AI-δ-GLMB、DI-δ-GLMB、ADI-δ-GLMB滤波器能对目标数进行无偏估计，估计标准差更小。

图3为不同算法的OSPA距离，可以看出：信息辅助的δ-GLMB相比标准δ-GLMB滤波器OSPA距离更小，且ADI-δ-GLMB滤波器OSPA距离最小，状态估计精度最高。由于δ-GLMB类滤波器利用多帧量测信息计算假设概率，当目标消失时，之前的量测信息仍会影响当前时刻的概率分布，导致对目标消失反应慢，引起较大的估计偏差，因此当目标消失时这些滤波器的OSPA距离均会出现较大的尖峰。

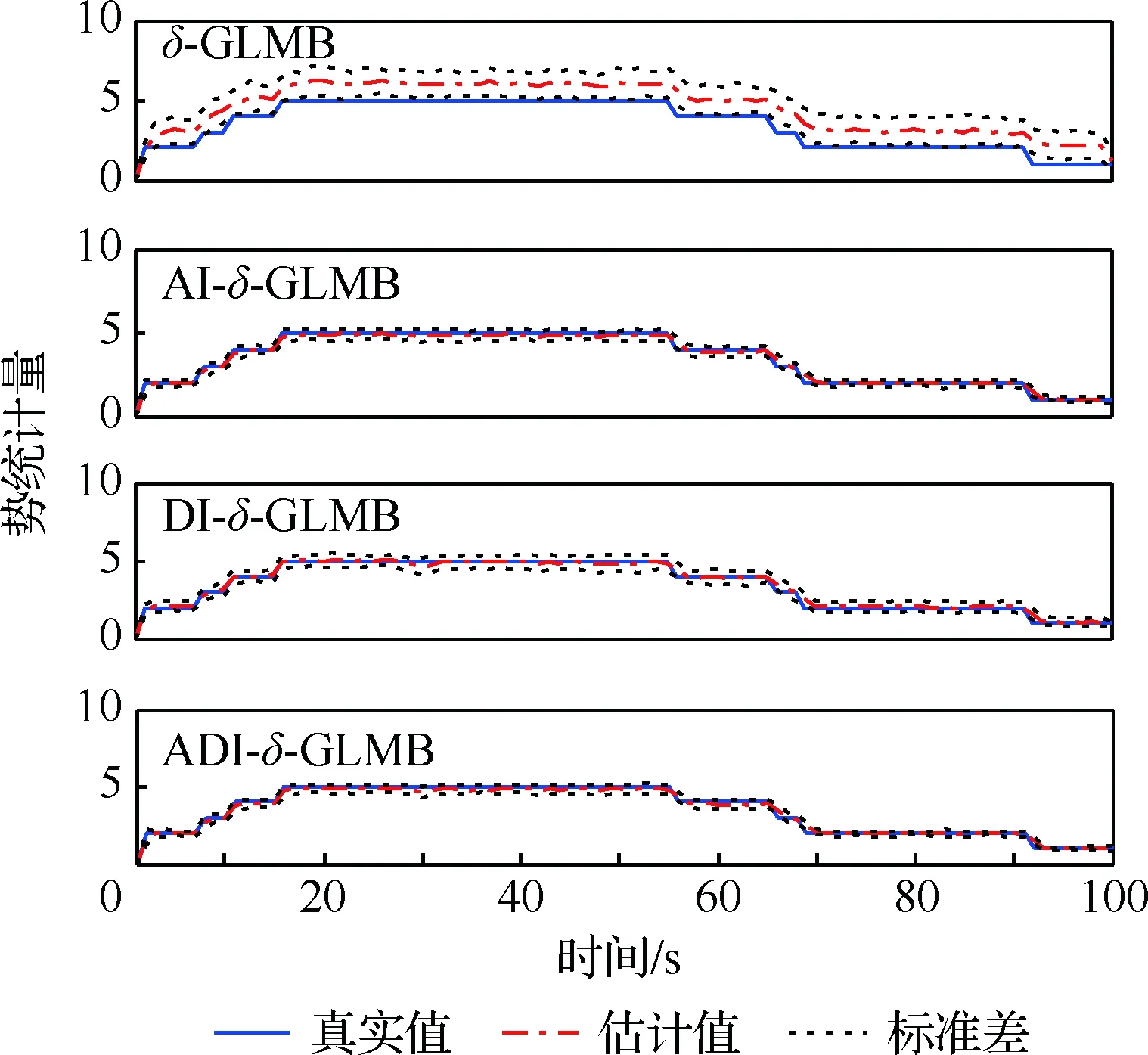
图2 不同算法势估计性能对比Fig.2 Comparison of estimated cardinality with different algorithms

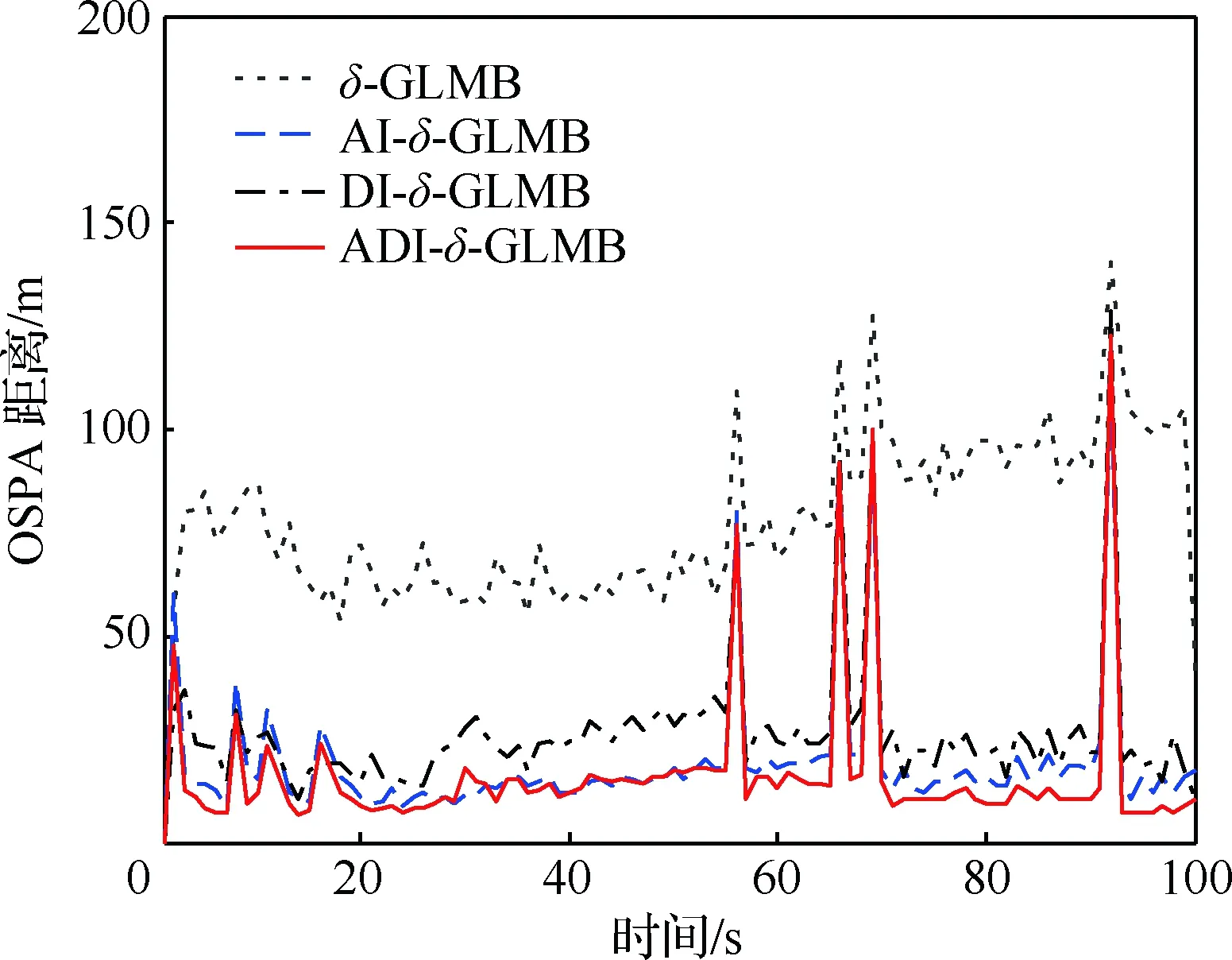
图3 不同算法的OSPA距离Fig.3 OSPA distance with different algorithms

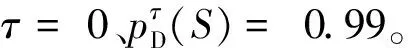
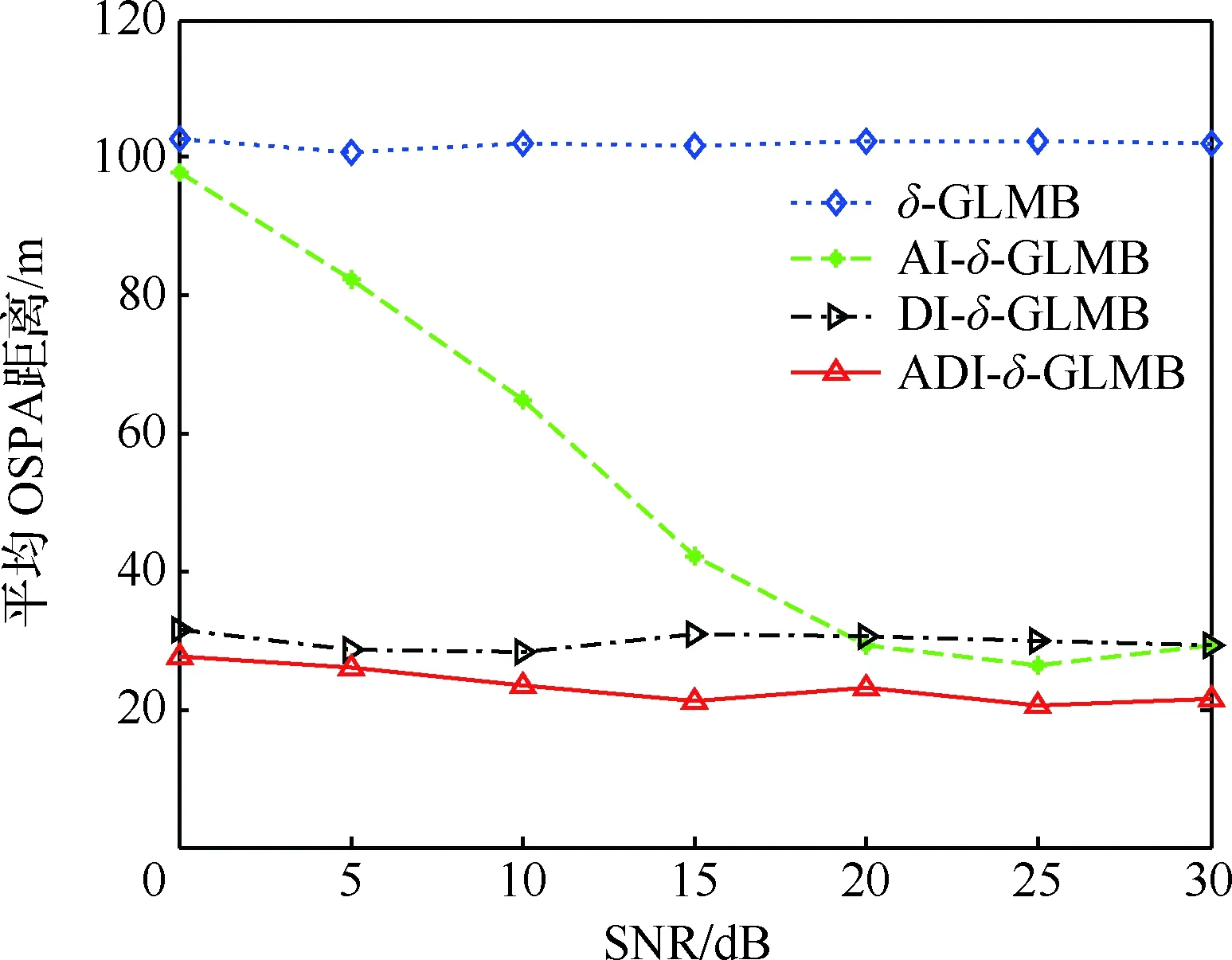
图4 不同SNR下平均OSPA距离对比Fig.4 Comparison of average OSPA distance with different SNRs

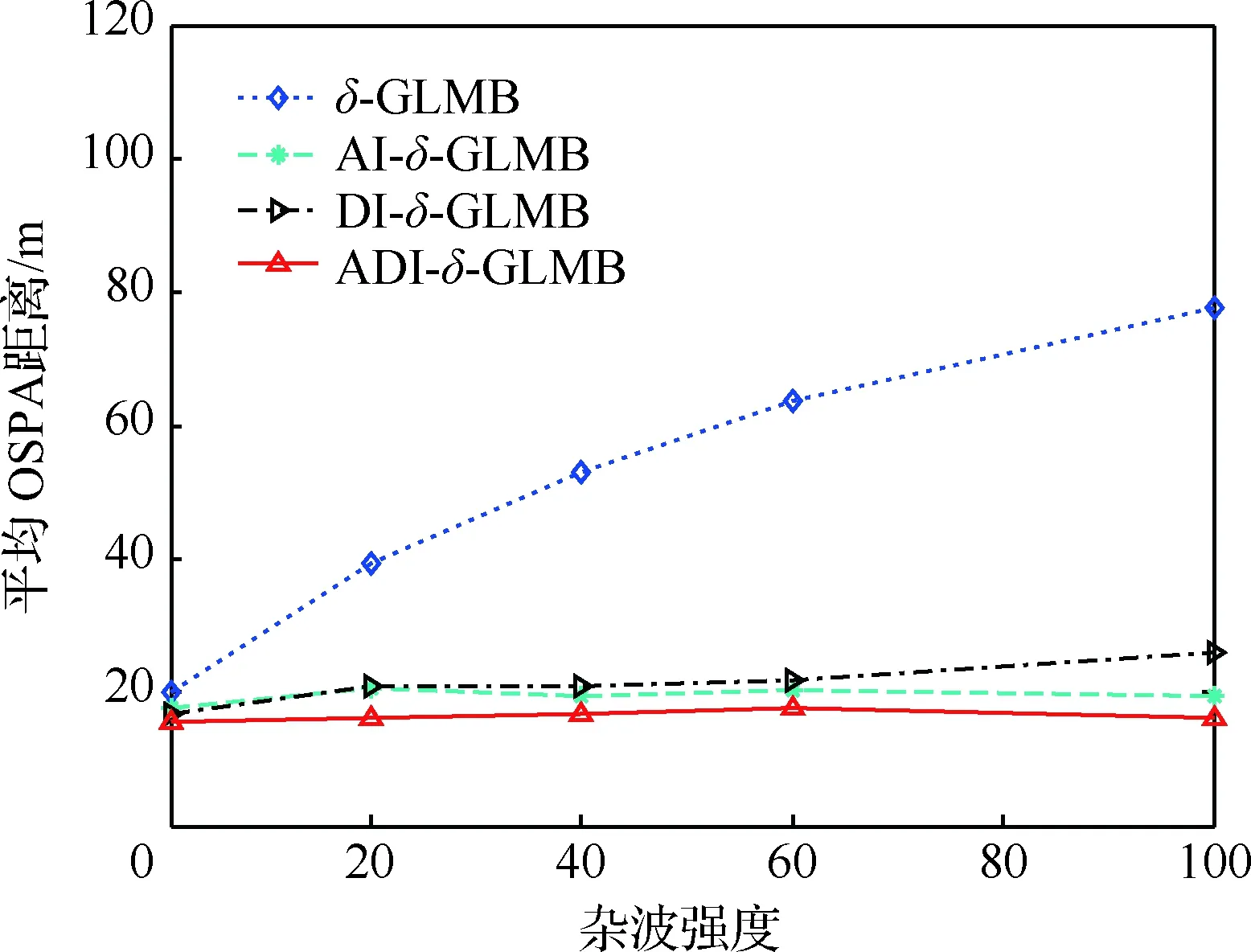
图5 不同杂波强度下平均OSPA距离对比Fig.5 Comparison of average OSPA distance with different clutter intensity

图5为不同杂波强度下算法的平均OSPA距离对比。可以看出，随着杂波强度的增加，标准δ-GLMB滤波器的平均OSPA距离也随之快速增大，说明其受杂波影响较大；而ADI-δ-GLMB滤波器平均OSPA基本保持稳定，说明其受杂波影响小，抗干扰能力强。

在i5-4590 3.30 GHz CPU，8G RAM，MATLAB 2011软硬件平台下，不同杂波强度下算法的平均运行时间对比如图6所示。可以看出，随着杂波强度的增加，标准δ-GLMB计算量快速增长，而AI-δ-GLMB、DI-δ-GLMB、ADI-δ-GLMB计算量增长缓慢。这是因为辅助信息的δ-GLMB采用位置、幅度、多普勒的联合量测似然，利用目标与杂波的幅度及多普勒信息差异，增大了真实航迹假设的权重，并减小了虚假航迹假设的权重，当进行假设裁剪处理时，可去除大量虚假航迹假设，减少需要处理的假设个数，从而降低计算量。

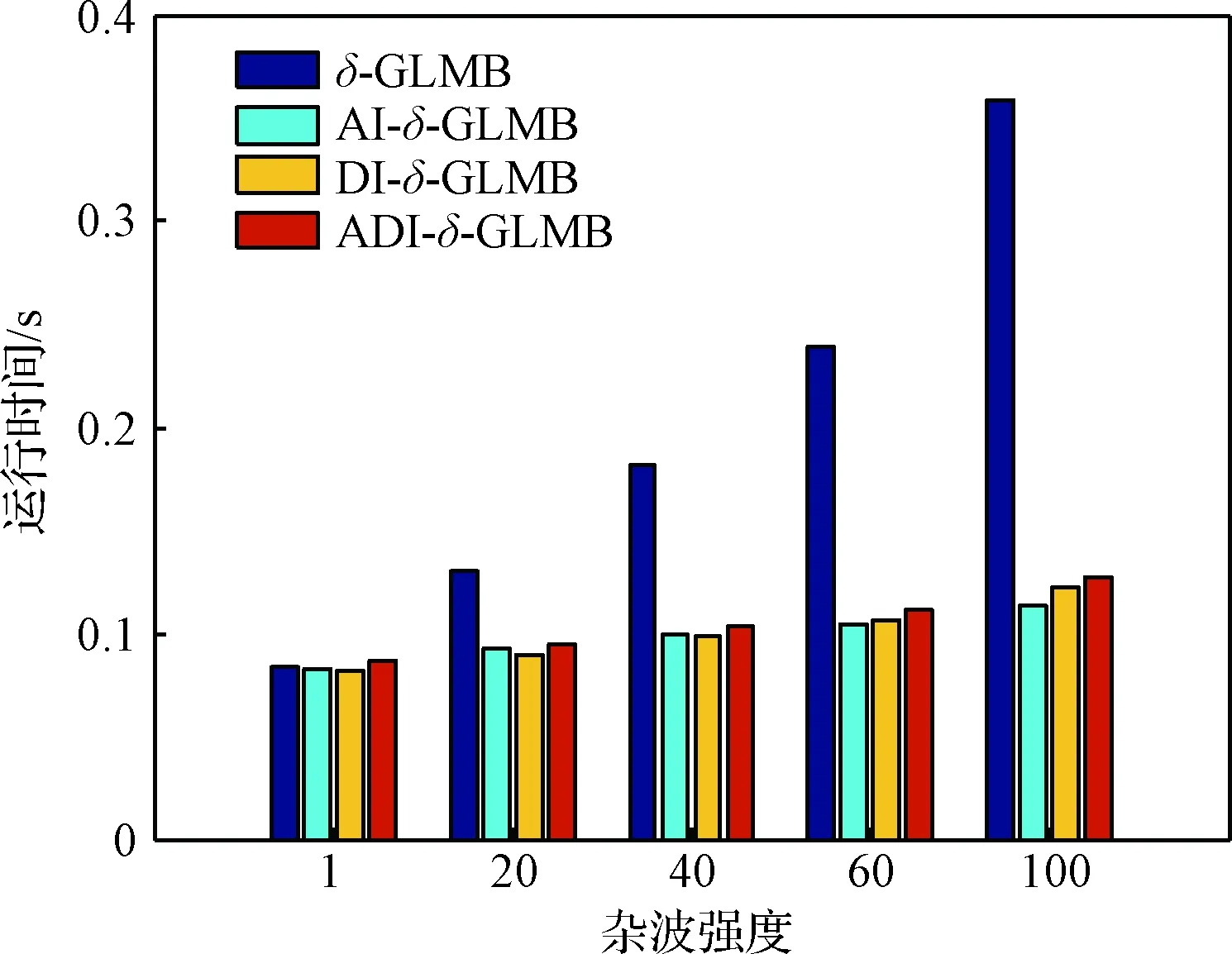
图6 不同杂波下平均运行时间对比Fig.6 Comparison of average execution time with different clutter

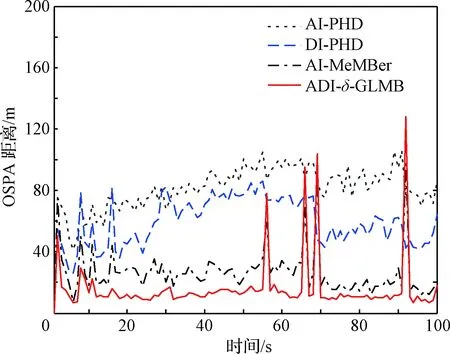
图7 不同算法的OSPA距离对比Fig.7 Comparison of OSPA distance with different algorithms

为进一步验证本文算法的性能，在上述实验条件下，对AI-PHD、DI-PHD、幅度信息多目标多伯努利(Amplitude Information MeMBer, AI-MeMBer)[9]及ADI-δ-GLMB几种滤波器进行对比。图7所示为不同算法的OSPA距离对比，可以看出：ADI-δ-GLMB相比其他算法OSPA距离更小，状态估计精度更高。

4 结 论

利用目标与杂波之间的幅度及多普勒信息差异，提出了一种ADI-δ-GLMB滤波器。

1) ADI-δ-GLMB滤波器能综合利用幅度及多普勒信息，相比仅利用单一辅助信息，具有更高的跟踪精度。当利用幅度信息无法对目标与杂波进行区分时，ADI-δ-GLMB会退化为DI-δ-GLMB；当多普勒信息无法获取时，则退化为AI-δ-GLMB。

2) 引入辅助信息后，有效提高了标准δ-GLMB滤波器的势估计稳定性及状态估计精度，并有效降低了高杂波下的计算量，且具有良好的杂波抑制能力；同辅助信息的PHD、MeMBer滤波器相比，ADI-δ-GLMB状态估计精度更高。