独立桨距控制对直升机飞行性能的影响

董晨，韩东，杨克龙

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

主动旋翼技术的出现，为进一步提升旋翼性能提供了新的发展途径，其中独立桨距控制技术是通过安装在旋转环上的作动器，实现桨叶的高阶谐波桨距变化。国内外的理论和实验研究[1-6]表明,独立桨距控制在直升机减振和旋翼降噪上有着较好的应用前景，对于增加高阶谐波桨距输入后可能带来的直升机需用功率变化的关注则相对较少。独立桨距控制的输入阶次、幅值和相位角等参数的变化对直升机性能的改变都有一定的影响，如何输入较优的独立桨距以减小旋翼的需用功率，并探讨性能提升的条件与机理是本文的主要研究内容。

早在20世纪50年代，Payne[7]就考虑了高阶桨距控制在延缓旋翼失速上的可能性,指出合适的高阶桨距输入可以有效推迟后行侧桨叶的失速。随后，对于高阶谐波控制的研究重点转移到旋翼的减振和降噪上[8],由于输入频率对高阶谐波控制的限制[9],缺少2阶桨距的输入不利于功率节省，后续研究人员逐渐开始研究基于桨距控制的独立桨叶控制。Swanson等[1]通过试验研究表明，斜下降飞行状态时，开环的独立桨距控制可有效降低BO-105直升机的整体噪声。Splettstoesser等[2]对比了具有独立桨距控制系统的直升机的试验结果和仿真计算结果，发现开环的独立桨距控制在降低桨涡干扰噪声和减振上有较大潜力。倪同兵等[3]基于一种综合噪声分析方法，模拟了桨涡干扰发生时的旋翼非定常气动载荷和噪声特性，分析了独立桨距控制的降噪机理。德国ZFL公司[4]为CH-53G直升机设计、制造和安装了一个实验性的独立桨距控制系统，可有效解决直升机振动问题，前飞速度为70 kn(1 kn=1.852 km/h) 时，减振效果最佳。Roget等[5]基于独立桨距控制方法开发了一种自适应控制算法用于减小旋翼桨毂振动，控制器成功减少了由桨叶差异引起的桨毂载荷的所有谐波量。孙超等[6]采用基于独立桨距控制的主动振动控制方法，对某电控旋翼进行了数值仿真，结果表明独立桨距控制方法的减振效果显著。

国外在独立桨距控制提升直升机性能方面也开展了一定的研究。笔者团队[10]较详细地总结了国外在独立桨距控制提升直升机性能方面的研究进展，指出了独立桨距控制在提升直升机最大飞行速度[11]、降低直升机高速飞行时的需用功率[12-13]以及提升旋翼性能[14-15]等方面有积极作用。上述研究主要基于2阶独立桨距控制对旋翼性能的影响，阻力系数发生改变[16-17]是其降低旋翼需用功率的物理机理。Yeo等[18]对比了具有独立桨距控制系统的黑鹰直升机风洞测试结果与CAMARDⅡ/OVERFLOW耦合分析结果，表明理论分析可较准确地反映直升机的功率变化趋势。Küfamann等[19]提出了一种局部桨距控制的方法，最高可降低旋翼7.61%的需用功率，比常规2阶独立桨距控制对旋翼性能的提升效果更好。国内方面，王超等[20]研究了2阶谐波桨距控制对旋翼性能的影响，指出直升机处于高速、大载荷飞行状态时，2阶桨距输入可改善桨盘平面迎角分布，推迟后行侧桨叶的失速，从而提升旋翼的性能。国内外针对不同输入阶次、幅值和相位角的独立桨距控制对直升机性能影响的研究相对较少。

本文在已验证的直升机飞行动力学模型基础上，以UH-60A直升机为样例，通过在旋翼上施加独立桨距控制，给出直升机的需用功率和升阻比的变化情况，着重分析独立桨距控制的输入阶次、幅值和相位角等参数对直升机飞行性能的影响情况，并探讨独立桨距控制提升旋翼性能的机理。

1 旋翼需用功率和直升机升阻比计算方法

1.1 直升机飞行动力学模型

建模方法参考文献[21], 基于叶素理论建立旋翼模型，桨叶采用带挥舞铰外伸量的刚性梁模型；由叶素所在位置的马赫数和迎角，查翼型气动参数表得到其剖面的气动力；旋翼诱导速度的计算采用Pitt-Peters动态入流模型[22]。挥舞运动影响气动力和力矩计算，根据桨叶惯性力、重力和气动力对挥舞铰的力矩平衡，通过迭代至挥舞响应收敛，旋翼上的力和力矩通过叶素上的力和力矩沿径向和展向积分，其中，挥舞响应的计算采用韦恩·约翰逊的经验方法[23]，即

(1)

(2)

式中：Mβ为挥舞力矩；Iβ为 挥舞惯性矩。

尾桨模型中，计算出的尾桨拉力一方面可用来平衡旋翼反扭矩，一方面还会参与直升机横向力的配平。机身受力情况复杂，计算过程中可假设其为具有特定气动力和力矩的刚体模型。

配平模型根据直升机平衡条件确定直升机稳态飞行所需的操纵量和姿态角，操纵量包含旋翼的总距、纵横向周期变距和尾桨的总距，姿态角包含机体俯仰角θF和侧倾角φF，配平中需考虑的力和力矩主要有：直升机重力W、旋翼拉力TMR、旋翼后向力HMR、旋翼侧向力YMR、旋翼滚转力矩MxMR、旋翼俯仰力矩MyMR、反扭矩QMR、尾桨拉力TTR、机身阻力D、机身俯仰力矩MyF和机身滚转力矩MxF，如图1所示。可得直升机六自由度平衡方程为

(3)

其中：以体轴系为参考坐标系，xCG和yCG分别为直升机重心与x轴和y轴的距离；h和hTR分别为旋翼桨毂与直升机重心和尾桨桨毂在z轴方向的距离；lTR为尾桨桨毂与直升机重心在x轴方向的距离。

采用牛顿迭代法求解直升机的平衡方程组，直至迭代收敛，得出稳态响应时的旋翼操纵量和机体姿态角，进而计算得出旋翼需用功率和直升机升阻比，计算流程如图2所示。旋翼提供升力和拉力，其中升力为TMRcosαTPP，等效阻力由功率消耗计算，直升机的升阻比为[24]

(4)

式中：αTPP为桨尖平面迎角；P为旋翼需用功率；W为直升机起飞重量；V∞为直升机前飞速度。

图1 直升机前飞受力分析图Fig.1 Forces and moments acting on a helicopter in free flight

图2 性能计算流程图Fig.2 Flowchart of performance prediction

1.2 桨距变化

旋翼桨叶的桨距一般由2部分组成，旋翼的总距和纵横向周期变距，即0阶和1阶的输入。独立桨距控制的旋翼，可提供更高阶次的谐波量θIBC，其表达式为

θ=θ0+θ1ccosψ+θ1ssinψ+θIBC

(5)

θIBC=Ancos(nψ+φn)

(6)

式中：θ为旋翼的桨距；θ0为旋翼总距；θ1c和θ1s分别为旋翼的横向周期变距和纵向周期变距；An、n和φn分别为独立桨距的幅值、阶次和相位角。

1.3 模型验证

采用UH-60A直升机的飞行数据[25]验证模型的正确性，其旋翼和尾桨的参数[26-27]如表1和表2所示。尾桨桨毂中心到旋翼轴的距离为9.93 m，旋翼桨毂至直升机重心的垂直距离为1.78 m，图3给出了直升机起飞重量分别为8 323.3、9 474.7、10 627.0和11 651.3 kg(对应直升机重量系数CW分别为0.006 5、0.007 4、0.008 3和0.009 1)时的飞行测试数据与计算数据对比，由图3可知，本文模型计算所得的需用功率与测试值吻合，证明此模型可用于分析直升机的飞行性能。

表1 旋翼参数Table 1 Parameters of main rotor

表2 尾桨参数Table 2 Parameters of tail rotor

2 样例计算与分析

为讨论独立桨距控制对直升机飞行性能的影响，在给定输入阶次后，研究不同输入幅值和相位角时，旋翼需用功率和升阻比的变化情况，并寻求较佳输入以获得较大的旋翼性能提升。

2.1 2阶独立桨距控制

输入2阶幅值为1°的独立桨距，直升机起飞重量为10 627 kg(CW=0.008 3)时，旋翼的需用功率及其减少程度随前飞速度和输入相位角的变化如图4和图5所示。输入相位角为225°时，旋翼的需用功率最多可降低2.1%，过大或过小的相位角难以带来更多的功率节省。该相位角下，前飞速度较小时，旋翼需用功率变化不大，高速时，旋翼需用功率有较明显降低，说明2阶(2P)独立桨距控制适宜于提升直升机高速飞行时的飞行性能。

图4 不同前飞速度和输入相位角下的需用功率(CW=0.008 3, 2P)Fig.4 Power required at different forward speeds and input phase angles (CW=0.008 3, 2P)

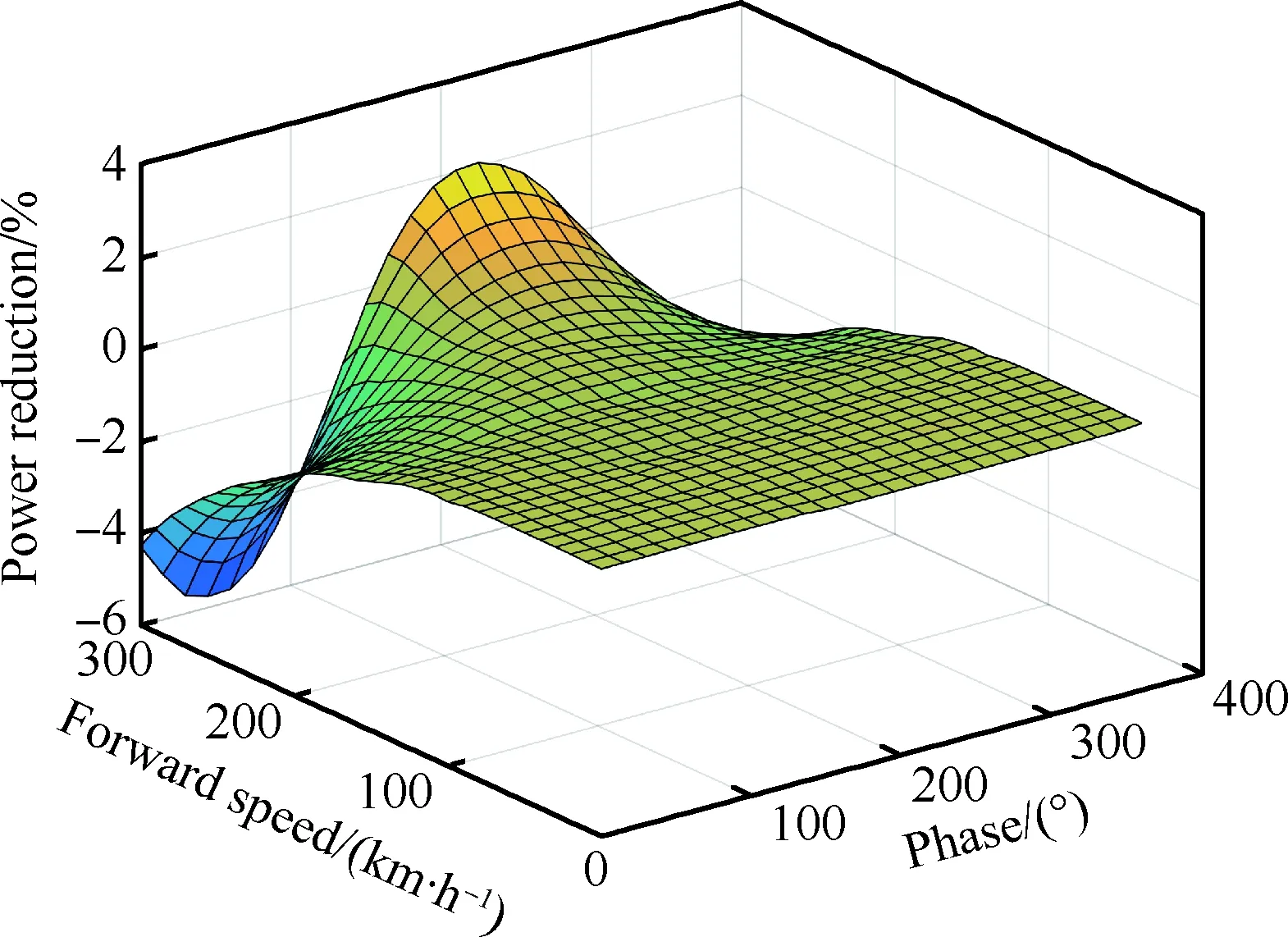
图5 不同前飞速度和输入相位角下的功率减少程度(CW=0.008 3, 2P)Fig.5 Power reduction at different forward speeds and input phase angles (CW=0.008 3, 2P)

图6给出了直升机分别以100、200、300 km/h的速度前飞时，直升机升阻比随输入相位角的变化情况，前飞速度较小(100 km/h)时，升阻比基本没有变化；大速度前飞(300 km/h)时，升阻比提升明显，最优相位角为225°，与需用功率变化趋势一致。

输入相位角为225°时，直升机升阻比及其提升百分比随输入幅值的变化如图7所示。中低速前飞时，随着输入幅值的增大，升阻比不升反降；高速前飞时，升阻比逐渐增大，但增大幅值较小。输入幅值A2为1°、前飞速度为300 km/h时，升阻比增大2.1%，输入幅值过大或过小均难以增强提升效果。

直升机的起飞重量增加至11 651.3 kg(CW=0.009 1) 时，旋翼需用功率减少的百分比随前飞速度和相位角的变化如图8所示，需用功率变化趋势与起飞重量为10 627 kg(CW=0.008 3)时相似，高速时，增重后的旋翼需用功率的降低幅度更大，输入相位角为230°时，旋翼需用功率最多可降低4.1%。

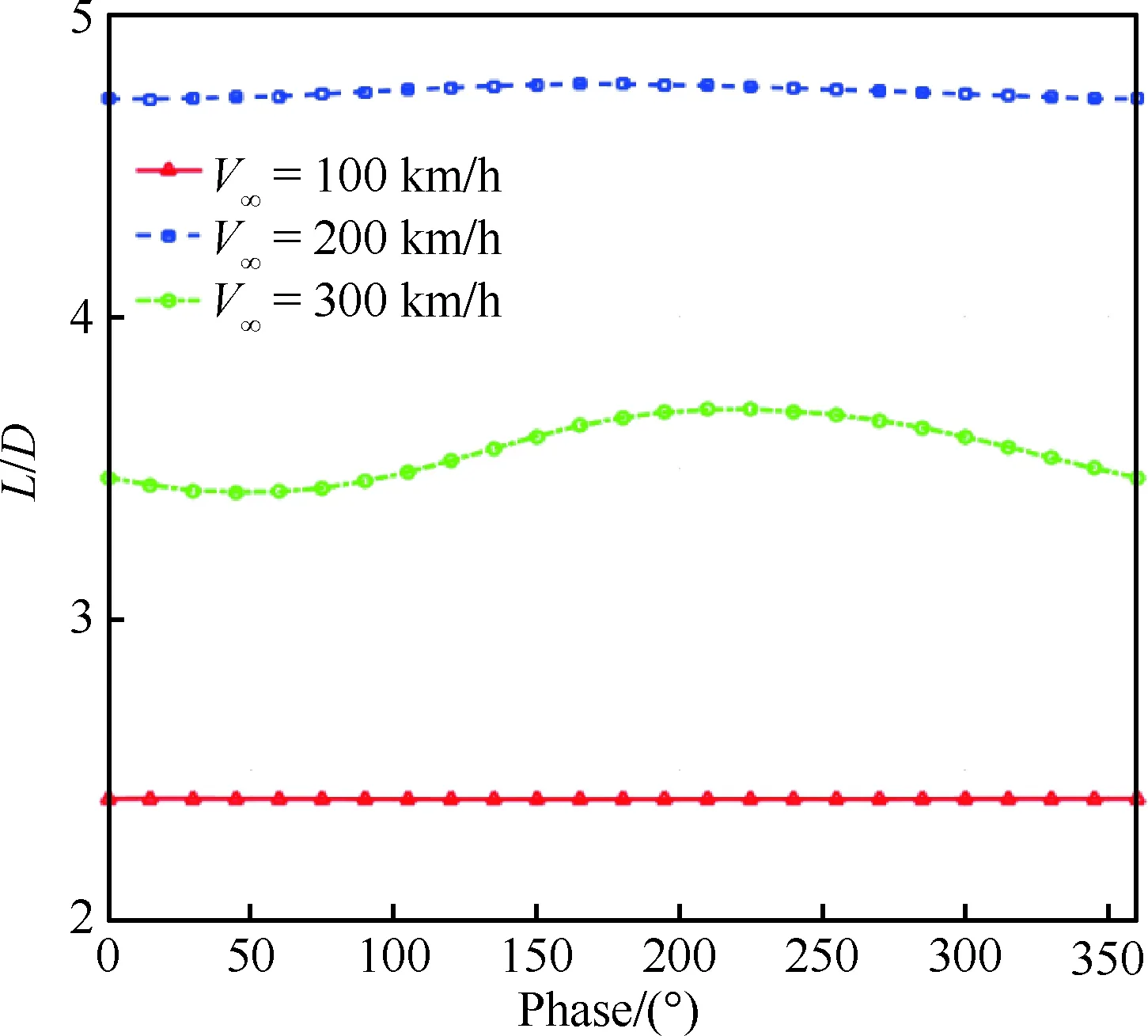
图6 升阻比随输入相位角的变化(CW=0.008 3, 2P)Fig.6 Lift to drag ratio vs input phase angle (CW=0.008 3, 2P)

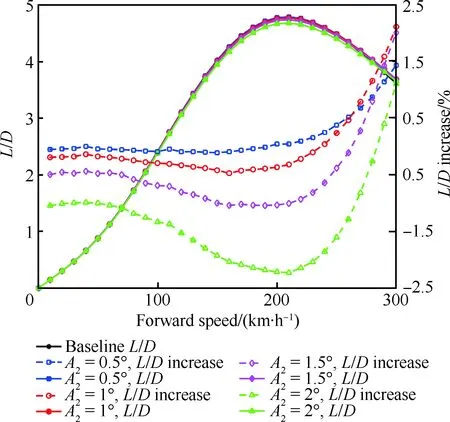
图7 不同输入幅值下升阻比和升阻比提升情况(CW=0.008 3, 2P)Fig.7 Lift to drag ratio and increase of ratio at different amplitudes (CW=0.008 3, 2P)

图8 不同前飞速度和输入相位角下的功率减少程度(CW=0.009 1, 2P)Fig.8 Power reduction at different forward speeds and input phase angles (CW=0.009 1, 2P)

输入相位角为230°时，升阻比及其提升百分比如图9所示，中低速时，增加独立桨距输入反而减小了直升机的升阻比，且随着输入幅值的增加，降低幅度也增加；高速时，直升机的升阻比有了明显的增加，与需用功率变化趋势一致。前飞速度为300 km/h时，1°和1.5°的独立桨距输入分别增大了直升机4.2%和4.1%的升阻比，0.5°和2°的桨距输入则提升较少，分别为2.9%和2.8%，相比起飞重量为10 627 kg(CW=0.008 3)时的最大提升百分比达2.1%，升阻比增加明显，说明起飞重量较大时，2阶独立桨距控制对直升机性能提升效果更好。

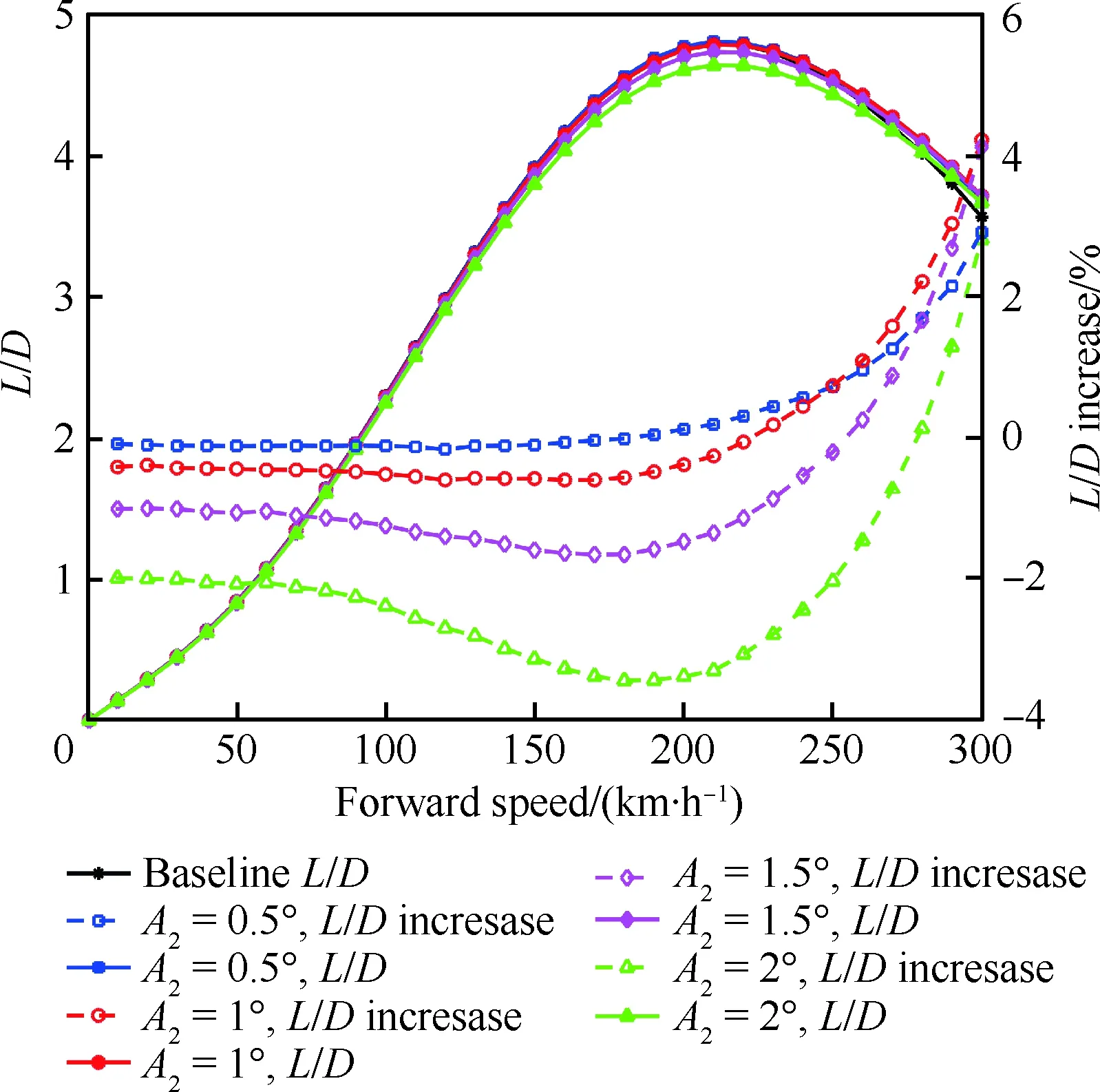
图9 不同输入幅值下升阻比和升阻比提升情况(CW=0.009 1, 2P)Fig.9 Lift to drag ratio and increase of ratio at different amplitudes (CW=0.009 1, 2P)

2.2 3阶独立桨距控制

直升机起飞重量为11 651.3 kg(CW=0.009 1)、输入阶次为3阶(3P)、输入幅值为1°时，需用功率及其减少程度随相位和前飞速度的变化如图10 和图11所示。输入相位角为195°时，旋翼需用功率降低最多，可达0.5%，相位角继续增大或减小均不利于提升旋翼的性能。最优相位角下，高速时，旋翼的需用功率可降低，降低幅度小于2阶独立桨距输入。

图12给出了直升机起飞重量为11 651.3 kg(CW=0.009 1)，不同输入幅值时，升阻比及其提升百分比随前飞速度变化情况。输入幅值A3为1.5°和2.0°时，升阻比在计算速度范围内没有增加，且在210 km/h左右时下降较多，0.5°和1.0°的输入幅值在中低速时同样会使升阻比减小，高速时，升阻比略有增加，但增加幅值很小，不到1%，说明3阶的独立桨距控制提升旋翼性能的效果有限。

图12 不同输入幅值下升阻比和升阻比提升情况(CW=0.009 1, 3P)Fig.12 Lift to drag ratio and increase of ratio at different amplitudes (CW=0.009 1, 3P)

2.3 4阶独立桨距控制

直升机起飞重量为11 651.3 kg(CW=0.009 1)，图13给出了4阶(4P)输入幅值A4为1°时，需用功率随前飞速度和输入相位角的变化情况，输入相位角为160°时，旋翼需用功率降低最多。不同输入幅值时，需用功率减少程度如图14所示，与2阶和3阶的桨距输入相比，4阶桨距输入并不能降低旋翼的需用功率，反而在所研究的速度范围内有所增加，说明4阶的独立桨距控制不适合用来提升旋翼的性能。

图13 不同前飞速度和输入相位角下的需用功率(CW=0.009 1, 4P)Fig.13 Power required at different forward speeds and input phase angles (CW=0.009 1, 4P)

图14 不同输入幅值下的功率降低幅度(CW=0.009 1, 4P)Fig.14 Power reduction at different amplitudes (CW=0.009 1, 4P)

2.4 2阶+3阶独立桨距控制

前述分析结果表明，2阶和3阶的桨距输入均可在一定程度上提升旋翼的性能，输入幅值为0.5°和1°时，提升效果相对较好。考虑同时施加2阶和3阶(2P+3P)的独立桨距控制，其提供的高阶谐波量为

θIBC=A2cos(2ψ+φ2)+A3cos(3ψ+φ3)

(7)

式中：A2、φ2和A3、φ3分别为2阶和3阶独立桨距的幅值和输入相位角。

直升机起飞重量为11 651.3 kg(CW=0.009 1)，图15和图16给出了同时输入2阶和 3阶的独立桨距、输入相位分别为230°和195°时，旋翼需用功率及其降低幅度的变化曲线。中低速时，需用功率变化较小，总体呈增大趋势；高速时，旋翼需用功率下降，相比单独输入2阶或3阶的独立桨距，需用功率下降程度更大；前飞速度为300 km/h时，2阶 幅值为1°耦合3阶幅值为0.5°的独立桨距输入降低了旋翼4.5%的需用功率，其余3种情况(2P，A2=0.5°)+(3P,A3=0.5°)、(2P,A2=1°)+(3P,A3=1°)、(2P,A2=0.5°)+(3P,A3=1°)分别降低了3.3%、3.7%和2.8%的需用功率。说明2阶耦合3阶的独立桨距控制对旋翼性能的提升效果更佳。

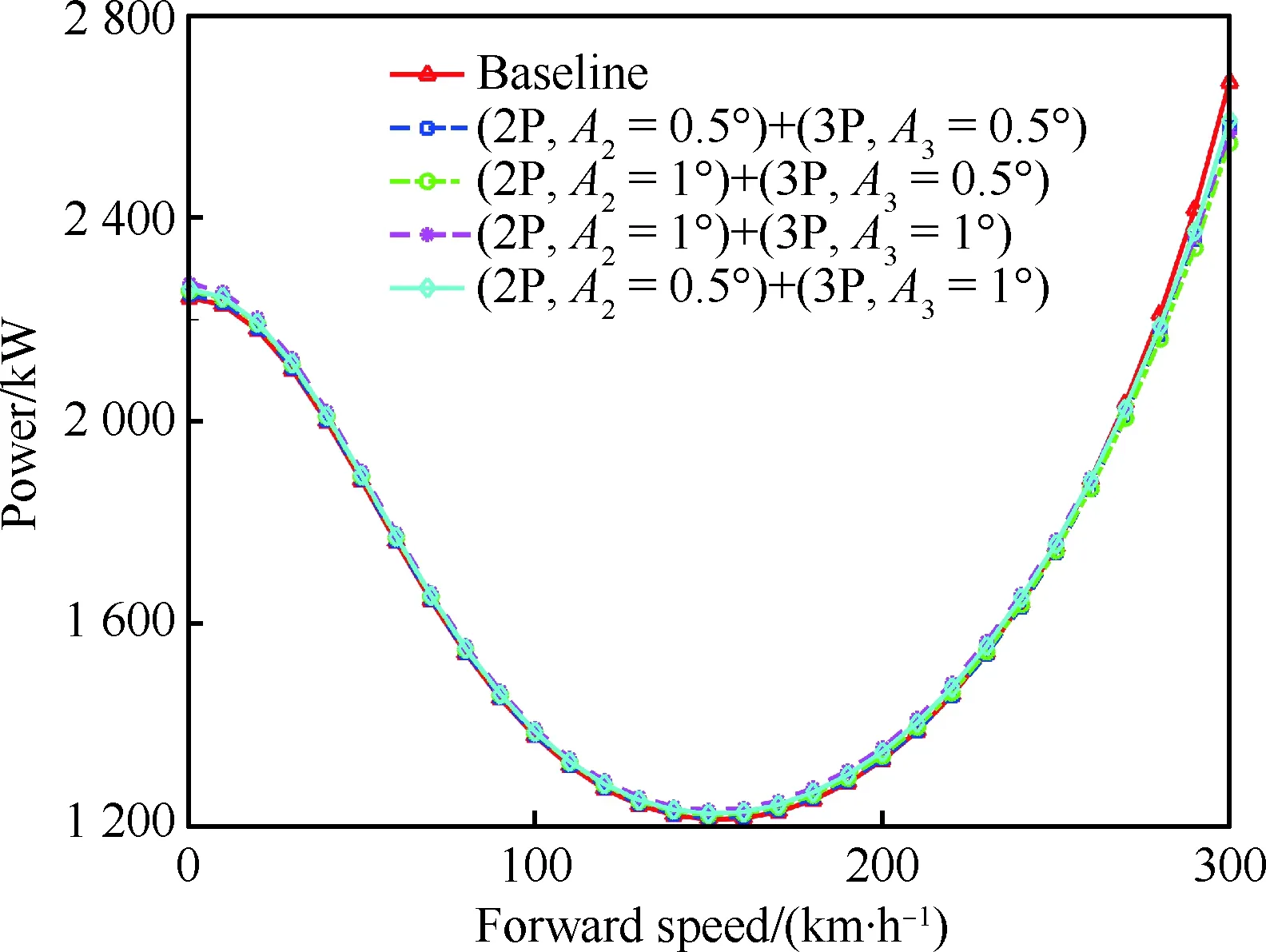
图15 不同前飞速度的需用功率(CW=0.009 1, 2P+3P)Fig.15 Power required at different forward speeds (CW=0.009 1, 2P+3P)

图16 不同前飞速度下功率降低幅度(CW=0.009 1, 2P+3P)Fig.16 Power reduction at different forward speeds (CW=0.009 1, 2P+3P)

不同输入幅值时的直升机升阻比变化曲线如图17所示，2阶耦合3阶的桨距输入明显进一步提升了直升机的升阻比。中低速时，独立桨距输入仍不利于提升升阻比，高速时，直升机升阻比有较明显的提升，提升效果比单独施加2阶或3阶独立桨距更好。前飞速度为300 km/h时，2阶幅值为1°和3阶幅值为0.5°的桨距输入分别可使直升机的升阻比提升4.2%和0.7%，二者同时输入则可提升4.7%。另外，同时输入2阶和3阶的独立桨距，对直升机的性能提升效果比单独输入3阶独立桨距的效果大很多，相比单独输入2阶桨距的效果则提升有限，证明输入2阶耦合3阶的独立桨距，对旋翼性能提升起主要作用的是2阶 独立桨距控制。

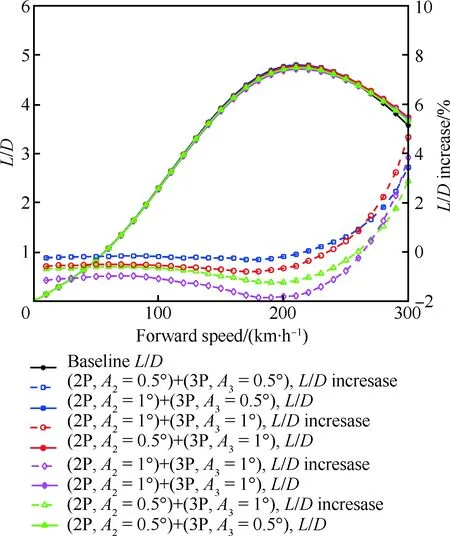
图17 不同输入幅值下升阻比和升阻比提升情况(CW=0.009 1, 2P+3P)Fig.17 Lift to drag ratio and increase of ratio at different amplitudes (CW=0.009 1, 2P+3P)

3 旋翼性能提升机理探讨

直升机的起飞重量为11 651.3 kg(CW=0.009 1)，2阶独立桨距输入幅值为1°，3阶独立桨距输入幅值为0.5°，前飞速度为300 km/h。直升机处于高速飞行状态时，后行桨叶易出现失速，导致旋翼的需用功率大大增加，不利于提升直升机的性能，通过独立桨距控制可改善桨盘平面迎角分布情况，一定程度上缓解此问题。如图18所示，基准桨叶剖面迎角最大值在12°左右，接近阻力发散对应迎角。施加2阶独立桨距控制后，旋翼前行侧桨叶迎角变化不大，后行侧桨叶迎角有了较明显的减小，部分区域靠近桨尖处的迎角减小了约1°，这有助于推迟后行侧桨叶的失速，但由于迎角减小程度较小，提升旋翼性能的效果也较有限。3阶的独立桨距输入对于旋翼桨叶剖面迎角改变不大，小于2阶独立桨距输入对后行侧桨叶迎角的影响，只有部分区域略微减小，因而对旋翼性能的提升效果也很小。同时施加2阶和3阶 的独立桨距控制，后行侧桨叶迎角明显变化，剖面迎角最大值降至11°左右，相比单独输入2阶或3阶独立桨距的效果要好，可更有效缓解失速问题，对旋翼性能的提升效果也最佳。

图18 不同输入下桨盘迎角分布情况Fig.18 Distribution of angle of attack over rotor disk with different inputs

图19(a)～图19(c)给出了无独立桨距控制和分别增加2阶、 3阶独立桨距输入时，旋翼桨盘平面阻力系数的分布，图19(d)为2阶幅值为1°耦合3阶幅值为0.5°的独立桨距输入时桨盘平面阻力系数的分布情况，阻力系数定义为[28]

(8)

式中：d为叶素阻力；ρ为空气密度；UB为流向叶素的相对气流合速度；c为桨叶弦长。

由图19可知，2阶的独立桨距控制较明显地降低了桨叶的阻力系数，前行侧部分区域阻力系数略有减小，后行侧靠近桨尖区域的阻力系数变化明显，有助于降低旋翼的需用功率。3阶的独立桨距控制对阻力系数分布的影响不如2阶的桨距输入，与基准旋翼相比变化较小，因而对旋翼性能的提升也较有限。2阶耦合3阶的独立桨距控制进一步减小了桨叶阻力系数，尤其是后行侧桨叶，且效果比单独的2阶或3阶桨距输入效果更好，因而对旋翼性能的提升效果也更佳。

4 结 论

在已验证了的直升机性能分析模型基础上，通过输入不同阶次、幅值和相位角的独立桨距，分析了直升机需用功率和升阻比等参数的变化，研究了独立桨距控制对旋翼性能的影响，并探讨了相关影响机理，得出如下结论：

1) 独立桨距控制在高速状态下可降低旋翼的需用功率、提升直升机的升阻比，且在直升机起飞重量较大时，提升效果更明显，2阶的独立桨距控制，分别可使起飞重量为10 627 kg(CW=0.008 3)和11 651.3 kg(CW=0.009 1)的直升机升阻比最多提升2.1%和4.2%；中低速时，不利于提升旋翼的性能。

2) 2阶的独立桨距控制对旋翼性能提升效果相对较好，输入相位角为225°、幅值为1°时，最多可降低4.1%的旋翼需用功率；3阶的独立桨距输入对旋翼性能提升有限，输入相位角为195°、幅值为0.5°时，在高速时最多可使需用功率下降0.7%，变化幅值较小；4阶的独立桨距输入不利于提升旋翼的性能。

3) 2阶耦合3阶的独立桨距控制，对直升机飞行性能提升效果最佳，最多可使旋翼的需用功率降低4.5%，比单独输入2阶或3阶桨距提升效果更好，其中2阶独立桨距控制起主导作用。

4) 独立桨距控制提升旋翼性能的机理在于其可改善旋翼桨盘内的迎角分布，减小后行侧桨叶的剖面迎角和阻力系数，有效延迟失速，减小旋翼的需用功率，从而提升直升机的飞行性能。