超声速湍流密度脉动预测的神经网络方法
王正魁,靳旭红,朱志斌,程晓丽
中国航天空气动力技术研究院,北京 100074
红外制导导弹在大气层内飞行时,激波和湍流引起的流场介质不均匀分布,使光线产生折射和衍射等现象,从而导致探测图像发生畸变,这种现象被称为气动光学效应。气动光学效应会影响光学导引头对目标的追踪和识别能力,因此湍流流场及其气动光学效应研究对精确制导导弹的研究具有重要意义。
国外已有学者和团队利用此类方法评估或改进RANS模型。针对RANS方法中不同湍流模型对特定物理问题的适用性,有文献利用监督学习方法评估RANS方法所得结果的可靠性。其中第1种思路是通过评估所采取假设的准确程度来预测RANS方法所得结果的可靠度[7-9];第2种思路是直接分析雷诺应力张量的误差与平均流动特征间的关系[10];第3种思路是通过评估输运方程的准确性来评估RANS方法的可靠度[11-13]。
Tracey等[14]利用平板边界层的算例训练神经网络,使其掌握一方程Spalart-Allmaras模型中输运方程的规律。发现神经网络模型可预测平板边界层和翼型绕流,但对槽道流的预测效果较差。可见,神经网络方法在相似流场上也可体现出一定的泛化能力。此外,文献[15-17]将k-ε模型中的常数修改为可变系数,并用神经网络或贝叶斯方法来减小误差,发现系数具有大幅度的变化,改进模型更为准确。Duraisamy等[18-19]将Spalart-Allmaras模型中耗散项乘以一个函数。利用贝叶斯方法重构出该函数的空间分布,计算域中较高的函数值意味着较高耗散率。改进模型明显提高了非平衡湍流边界层中摩阻系数的计算精度。采用Sγ代表间歇因子γ的输运方程中生成项与耗散项之差,从RANS方法得到的参考流场中提取其分布,并利用标准的爬山算法选择特征量。然后,利用高斯过程和神经网络方法为Sγ建立模型,得到较好的预测效果。
考虑湍流的复杂性、方法的计算量和性能,本文采用神经网络方法进行函数回归,并对湍流密度脉动的均方值进行建模。首先,利用DNS方法模拟超声速壁湍流,并统计得到密度脉动均方值,密度和速度等平均场。然后,分别以密度脉动均方值和平均场的特征量作为样本的输出和输入,对神经网络进行训练和测试。因为密度脉动的均方值的影响因素众多,为提高模型的泛化能力,采用特征选择方法来筛选出合适的特征量作为输入。
1 研究方法
1.1 神经网络模型
为度量模型的性能,先定义性能度量为均方误差,即损失函数L(y,d)=(y-d)2,其中y为模型预测值,d为DNS的统计值。训练的过程即优化神经网络模型,使损失函数达到最小。
图1是双隐含层神经网络的示意图,其中Zm,n代表第m个隐含层的第n个神经元,连接不同层神经元的箭头代表突触权值。每个神经元只能有一个输出值,但可以有多个输入值。在第t次训练过程中,先根据输入和当前权值计算神经元j的诱导局部域,具体表达式为
(1)
式中:t为当前的训练回合数;wji为神经元j与i之间的突触权值;bj为神经元j的偏置(阈值);i、j均为神经元的编号,且i为j前一隐含层的神经元。
计算得到神经元的输出y(t)=φ(V(t)),激活函数φ代表了神经元对输入信号的响应,常用的有Logistic函数、双曲正切函数、线性整流函数ReLU以及具有自归一化能力的缩放指数线性单元SeLU。
文中隐含层选用SeLU,即

(2)

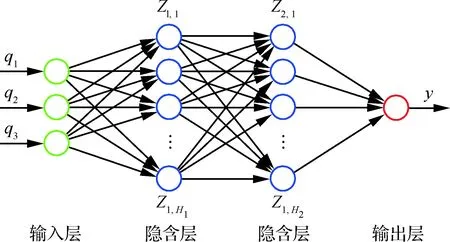
图1 神经网络示意图Fig.1 Schematic diagram of a neural network
输出层的激活函数为Logistic函数,即:φ(V)=(1+exp(-V))-1。
计算隐含层和输出层神经元的输出时,将前一层的输出作为其输入。逐层计算出所有神经元的输出后,根据实际响应y(t)和期望响应d(t)调整突触权值w和偏置b。下面给出突触权值和偏置的优化方法,采用附加动量项的梯度下降法,即:
(3)
式中:κ为梯度下降法的步长;α为动量因子;Δwji(t-1)、Δbj(t-1)为上一次训练中得到的变化量。根据微分的链式规则可得
2(yj(t)-dj)φ′(Vj(t))yi(t)
(4)
-2(yj(t)-dj)φ′(Vj(t))
(5)
定义神经元j的局域梯度为
(6)
则式(4)~式(5)可简化为
(7)
将式(7)代入式(3),并令学习率η=2κ可得
Δwji(t)=ηδj(t)yi(t)+αΔwji(t-1)
(8)
Δbj(t)=-ηδj(t)+αΔbj(t-1)
(9)
若神经元j为输出层神经元,则可将模型预测值与训练值之间的误差代入式(6),即可直接得到其局域梯度为
δj(t)=(dj(t)-yj(t))φ′(Vj(t))
(10)
若神经元j是隐含层神经元,不能直接得到其误差ej(t),则神经元j的局域梯度δj(t)需要由下一层与其直接相连的神经元的局域梯度向后递归确定,即反向传播算法。
(11)
为避免梯度下降算法收敛到非最优解的局部极小值,文中采用学习率退火的方案,即在训练过程中更新学习率,即
η=η0/(1+t/τ)
(12)
式中:η0为初始学习率;τ为搜索时间常数。
为降低模型的过拟合风险,采用复杂度正则化约束模型的复杂度,其思路是修改损失函数,使其包含标准的性能度量和复杂度惩罚项,即
L′=L(y,d)+λξ(w)/2
(13)
式中:λ为正则化参数,代表了性能度量与复杂度惩罚之间的权衡,是一个需要使用者调节的超参数;ξ(w)代表了模型的复杂度,文中取为突触权值w的2范数,则修改后的损失函数为
(14)
根据修改后的损失函数式(14),其对突触权值的偏导数应由式(7)修改为
(15)
突触权值的变化量由式(8)修改为
Δwji(t)=η(δj(t)yi(t)-λwji(t-1))+
αΔwji(t-1)
(16)
同时,为提高模型学习效率、降低收敛到局部极小值的风险,文中又采用批梯度下降法优化模型参数,在每次训练过程中使用的训练样本数为批尺寸。本文在训练初期采用较小的批尺寸,训练速度快;随着模型的收敛,逐渐增加批尺寸,在训练后期得到稳定的收敛结果。
1.2 样本数据获取方法
考虑到神经网络的训练需要大量的可靠数据,本文采用DNS方法计算得到超声速平板边界层的密度脉动、平均场以及湍流统计量,并提取特征量。为获取较高的空间分辨率,采用加权基本无振荡(Weighted Essentially Non-Oscillatory, WENO)的七阶格式[20-21],时间方向采用显式的二阶时间差分格式求解。
固壁边界条件为速度无滑移、等温壁;上游采用可压缩边界层的层流剖面作为入口边界,并施加周期性的速度扰动[22];远场和下游为出口边界条件,并预置缓冲层来抑制数值扰动反射的影响;展向采用周期性边界条件。
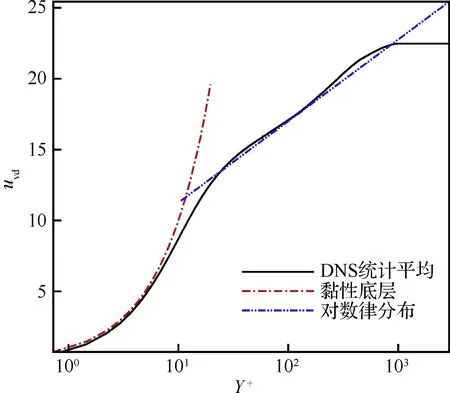
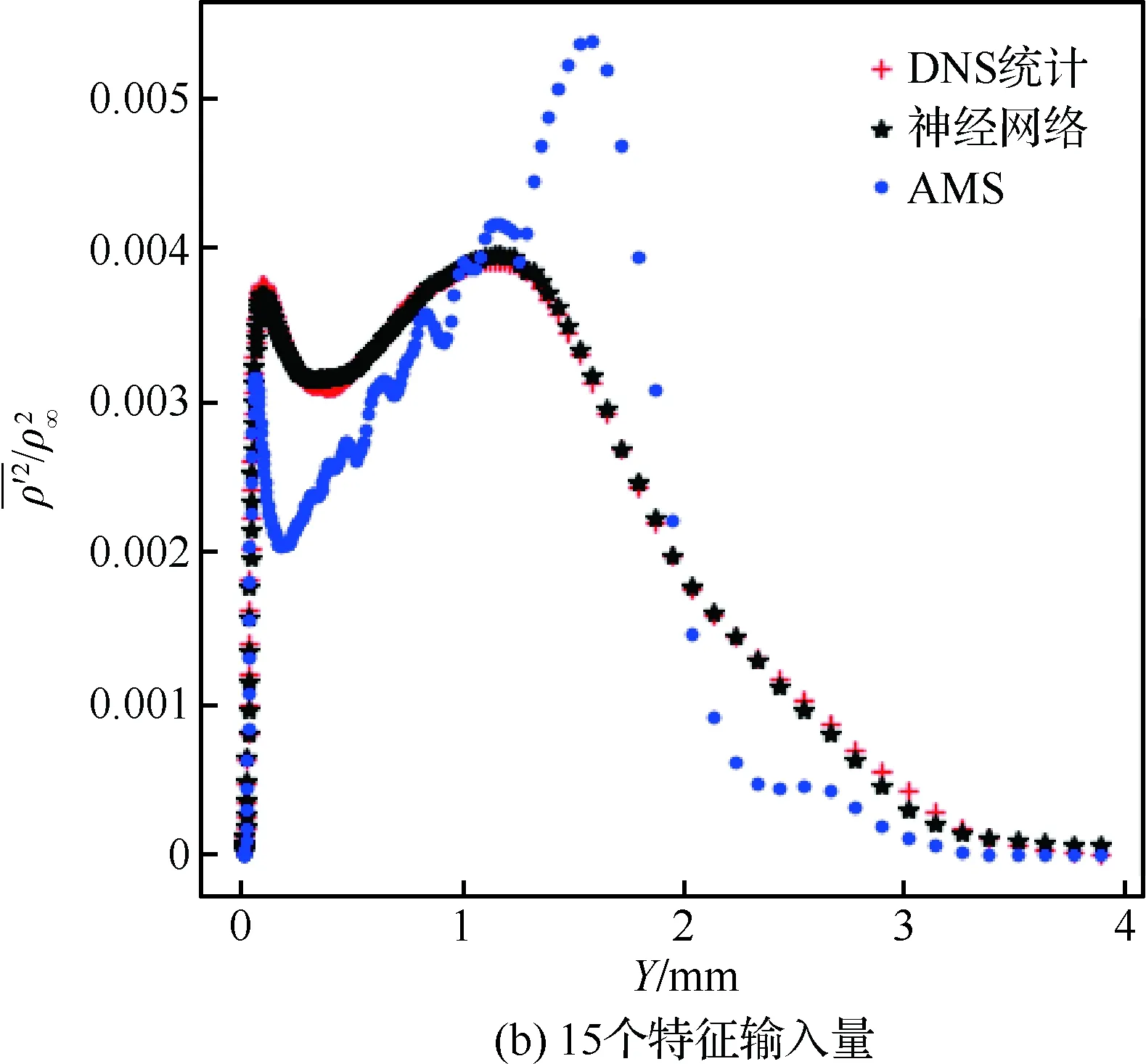
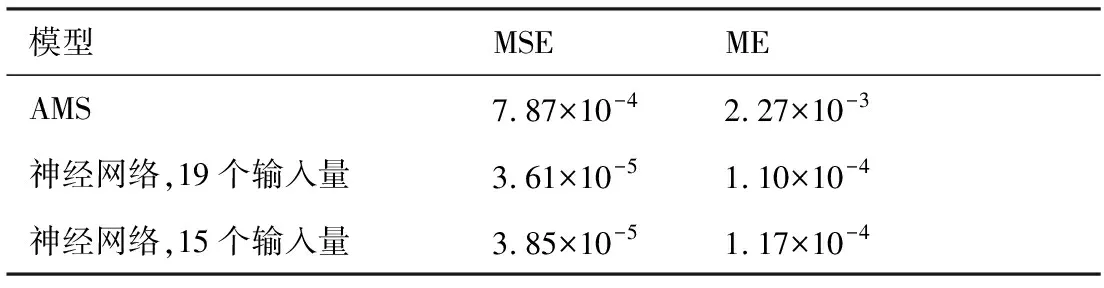
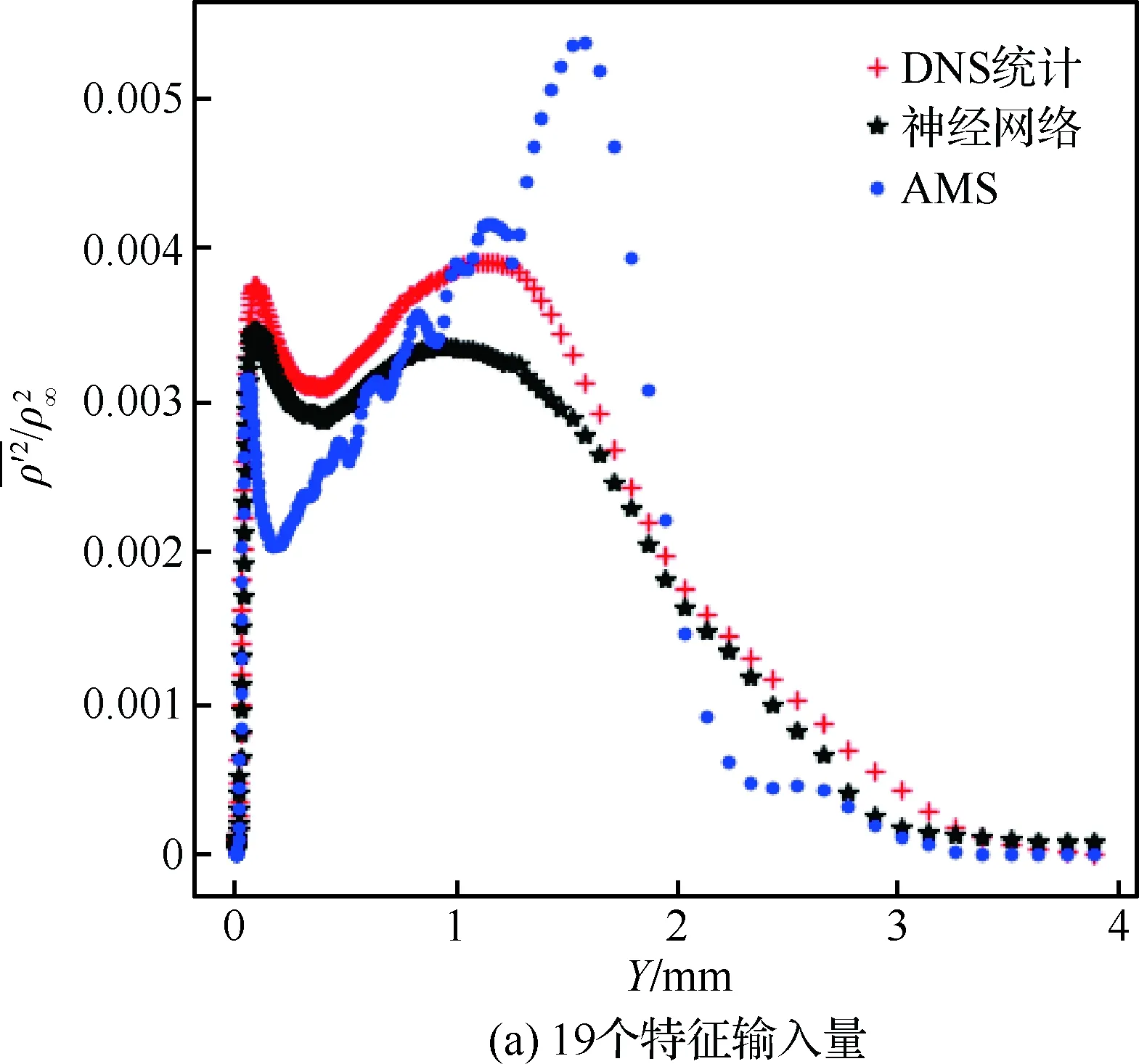
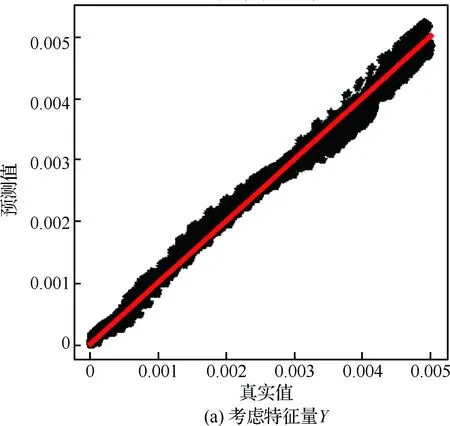
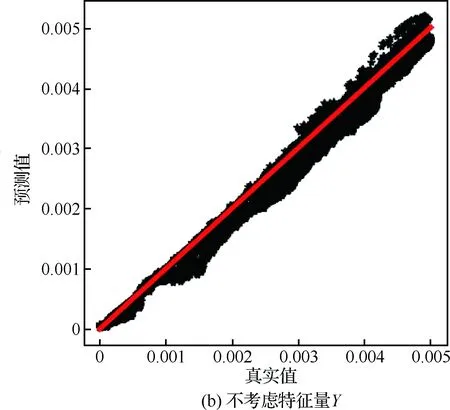
计算区域的流向长度LX=203.7 mm、法向高度LY=7.62 mm、展向宽度LZ=5.08 mm。网格在X和Z方向是均匀分布的,Y方向网格高度随着壁面法向距离的增加而增加。网格点数为2 000×200×200,边界层首层网格高度为ΔYmin=1.9×10-3mm,湍流区中0.33 图2给出了DNS模拟的速度与理论值的比较,可见DNS统计平均得到的流向速度在黏性底层、对数律层均与壁面律相符得较好,从而验证了流向速度的可靠性。进一步在相同来流条件下,将DNS模拟的密度时均值与文献[24]的结果进行比较,如图3所示(图中ρ∞为来流密度)。可见,本文模拟的密度与文献结果相符得较好,进一步验证了训练数据所得流场计算方法和结果的可靠性。 表1 不同算例的来流条件Table 1 Free-stream conditions of different cases 图2 Van Driest平均速度型的验证(Re=2.50×107)Fig.2 Validation of Van Driest mean velocity distribution (Re=2.50×107) 流场参数的时均值通过统计平均获取,即 (17) 式中:M为统计的时间样本数;θi为流场中速度、温度、密度等瞬时量。 (18) (19) (20) 不同的特征量之间可能相差多个数量级,湍动能和湍流耗散率等数量级大的特征对神经网络的影响过大,不利于训练神经网络,因此文中采用归一化方法消除特征量之间的量级差异。本文选用MapAverage函数将输入特征线性地变化到均值为0、标准差为1的状态,即 (21) 图4给出X=139.7 mm截面处DNS统计的密度脉动随Y+的变化。可见密度脉动在线性底层(Y+10)较小,在过渡层(10 图4 密度脉动随Y+的变化Fig.4 Density fluctuation as a function of Y+ 神经网络模型可能对“见过的”训练样本预测得非常好,而对“没见过”的新样本预测误差很大,即过拟合现象。因此,为合理地评估模型的泛化能力,采用留出法对模型进行训练和测试,即将整个样本空间分为训练集、验证集和测试集。在训练阶段,利用训练集中的样本(q,d)调整模型参数,在每训练一定次数后利用验证集的样本评估模型;在训练阶段结束后,选取在验证集上性能最佳的模型,并将测试样本的q输入到所得模型中,将其预测的密度脉动y与d进行比较,并评估模型的预测能力。文中不考虑转捩问题,从完全湍流区(152.4 mm 特征选择可降低问题和模型的复杂度,缓解过拟合问题。参考已有模型和先验知识,选取了19个待选特征量。先以全部待选特征作为输入量,对模型进行训练和测试;接着利用平均影响值算法,得到所有待选特征对模型输出的影响值,并进行排序;再假设影响值越大的特征越重要,逐一添加影响值大的待选特征,并对模型进行训练和测试,直到只剩下一个特征输入量时为止;确定在筛选特征过程中验证误差最小的模型,并将对应特征作为选择出的特征输入量。本文采用的特征选择过程如图5所示。 平均影响值算法可估计特征输入量对输出量的影响,即影响值,其绝对值表示影响程度,符号代表相关的方向。先以全部特征量作为输入,并训练得到一个模型;然后对其原有输入值逐个加减10%,并利用训练得到的模型预测对应的输出;其预测差值的绝对值在训练集的170 000个样本上的平均值即为该特征量对输出的影响值,对其按绝对值由大到小排序,即得到表2。表中v为法向速度,μt为湍流黏性系数,T为静温,ω为比耗散率。为降低特征量出现同时增大或减少的风险,随机地选择部分特征量取其相反数,如表2中-ρ、-T等。 图5 基于平均影响值算法的特征选择过程Fig.5 Process of feature selection based on mean impact value algorithm 表2 不同特征的影响值Table 2 Impact values of different features 平均影响值算法得到的影响值的绝对值代表了各个特征的重要程度,在每添加一个特征后对模型进行训练和测试,并记录对应的模型测试误差。下面定义两个误差。 1) 均方根误差,用以衡量模型的准确性,其表达式为 (22) 2) 最大误差,用以衡量模型的稳定性,其表达式为 (23) 实验过程中,选取不同输入特征量时,模型的均方根误差变化如图6所示。由图中可见,输入特征数为9、11、15和19时均方根误差比较小,其中误差最小的模型为15个输入量,即:-∂ρ/∂Y,∂ρ/∂X,-∂2ρ/∂Y2,u,v,-∂u/∂X,-∂u/∂Y,∂v/∂Y,Y,-T,-ρ,k,ε,μt,μ。对应的均方根误差为1.81×10-4。通过在实验中调节超参数,确定5个隐含层,从低到高分别有19、15、12、9和5个神经元,2范数的正则化参数取λ=3×10-8,动量因子α=0.2,初始批尺寸为50,初始学习率为η0=0.2。 为验证神经网络算法性能、程序的可靠性,先利用单一流场对模型进行训练和测试,评估结果如图7所示。可以看出,在密度脉动较大的区域内,神经网络方法较传统的AMS模型具有更高的预测精度。即使训练集和测试集不同,神经网络模型仍然能给出较好的预测结果,显示了一定的泛化能力。且在单一流场中特征选择对神经网络模型的预测效果影响不大,因为过拟合现象不严重。 图6 不同输入特征量的模型误差Fig.6 Errors of models with different input features 图7 特征选择对单一流场预测的影响Fig.7 Effect of feature selection on prediction of a single flow field 模型MSEMEAMS7.87×10-42.27×10-3神经网络,19个输入量3.61×10-51.10×10-4神经网络,15个输入量3.85×10-51.17×10-4 表3给出不同模型的测试误差,在特征选择前后,神经网络模型采用19个和15个输入量时在测试集上的均方根误差分别为AMS模型的4.59%和4.89%,在剖面上的最大误差分别为AMS模型的4.85%和5.15%。因此,相对于AMS模型,神经网络模型的预测精度显著提高。 神经网络模型在单一流场中对“没见过”的测试样本给出了很好的预测结果。然而,单一流场中的测试样本与训练样本之间具有很大的相似性,无法充分评估模型的泛化能力。而且,仅利用单一流场的数据训练神经网络模型,也无法获得较高的通用性,工程应用价值较低。 图8给出了多流场训练模型的预测结果,从图中可见,神经网络模型能够发现密度脉动的规律,且预测效果明显优于AMS模型。但在0.6 mm 图8 特征选择对多流场预测的影响Fig.8 Effect of feature selection on prediction of multiple flow fields 模型MSEME神经网络,19个输入量1.84×10-46.13×10-4神经网络,15个输入量1.81×10-45.93×10-4 表4定量地比较特征选择前后,神经网络模型的预测误差。在特征选择前后,神经网络模型采用19个和15个输入量在测试集上的均方根误差分别为AMS模型的23.4%和15.9%,在剖面上的最大误差分别为AMS模型的27.0%和26.1%。因此,相比于AMS模型,神经网络模型的预测结果更为准确和稳定,且特征选择进一步提高了模型的性能和精度。 上述模型中,输入量Y是一个与流场空间位置有关的特征量,为提高神经网络模型对复杂外形的适应性,对Y是否作为特征输入参数进行了进一步的评估。 在实验中重新调节超参数,确定5个隐含层,从低到高分别有13、12、10、10和8个神经元,2范数的正则化参数取λ=2.7×10-8,动量因子α=0.2,初始批尺寸为50,初始学习率为η0=0.2。下面对比是否考虑特征量Y时模型的测试结果。 图9分别给出了∂ρ/∂X、∂ρ/∂Y、μ、u、v、Y、S中是否考虑参数Y时,神经网络模型对所有测试样本的预测值随着真实值的变化情况,可见图中所有预测点都在斜率为1的直线附近变化,显示了神经网络模型很好的预测能力。比较是否考虑特征量Y情况下的测试结果可知,忽略特征Y会使得模型对中等强度密度脉动的预测误差增加。 图10对比了两个模型对同一个剖面的预测结果。从图9和图10中可见,加入相关模型的先验知识,特征选择后7个输入特征的模型可以得到比图8中15个输入特征更低的预测误差。而忽略特征量Y则降低了模型的预测精度。 模型定量的模拟误差见表5,从表中可见,考虑特征量Y(共7个输入量)时,神经网络模型在测试集上的均方根误差和在剖面上的最大误差分别为1.25×10-4和4.31×10-4,是19个输入量时模型的67.9%和70.3%。所以,在特征选择过程中,加入相关的先验信息可提高模型性能,在一定程度上避免了模型过拟合现象的发生。在忽略特征量Y后,神经网络模型在测试集上的均方根误差和剖面上的最大误差分别增加了24.0%和44.8%,特征量Y对模型泛化能力的影响需要在更广泛的算例中进一步评估。 图9 特征量Y对多流场测试的影响(回归线)Fig.9 Effect of feature Y on test of multiple flow fields (regression line) 图10 特征量Y对多流场预测的影响(剖面图)Fig.10 Effect of feature Y on predicting multiple flow fields (profile) 模型MSEME神经网络,考虑特征量Y1.25×10-44.31×10-4神经网络,不考虑特征量Y1.55×10-46.24×10-4 以考虑特征量Y时的模型为例,评估输入量误差对预测结果的影响。研究表明,模型对流向速度u的误差最敏感,其10%的误差对预测结果的影响也在10%左右。因此,总体来说该模型的鲁棒性较高。 仅利用CPU、单线程地预测完全湍流中240 000个样本的流场密度脉动共用时124 s,显著低于DNS和LES方法对计算机存储空间和计算量的要求,满足工程应用对计算效率的需求。 针对气动光学问题中对湍流密度脉动预测能力不足的问题,本文提出超声速湍流密度脉动预测的神经网络方法。先通过直接数值模拟方法得到不同来流单位雷诺数下超声速平板边界层的平均场、湍流参数,以及密度脉动,再利用神经网络方法从流场数据中挖掘规律,建立密度脉动模型,并评估其泛化能力。数值实验的结果表明: 1) 预测密度脉动的神经网络模型包含5个隐含层,从低到高分别有13、12、10、10和8个神经元,采用的初始批尺寸为50,2范数正则化参数λ=2.7×10-8,动量因子α=0.2,初始学习率为η0=0.2, 输入参数为∂ρ/∂X、∂ρ/∂Y、μ、u、v、Y和S这7个特征量,训练模型并取得了较好的预测精度。 2) 相对于传统模型,该方法在极大地降低对湍流理论等先验信息依赖的同时,也显著提高了预测能力。 3) 对不同流场中密度脉动的评估结果表明,本文所发展的方法具有一定的泛化能力。 4) 利用模型先验信息对输入参数进行特征选择,模型的精确度和稳定性得到了进一步提升。 本文探索了神经网络方法在超声速湍流问题中的应用,研究是初步的,模型的泛化能力和对其他外形的适应能力还有待于进一步评估。



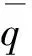


2 特征选择及泛化能力评估
2.1 平均影响值算法






2.2 加入先验信息




3 结 论

