带源项的吸引-排斥趋化模型解的有界性

戴 超， 陶有山

(东华大学 理学院， 上海 201620)

趋化性是由化学信号的浓度梯度引起的细胞偏向运动。趋化吸引是指细胞朝化学信号浓度增大的地方迁移，而趋化排斥是指细胞朝远离化学信号浓度增大的地方运动。著名的趋化数学模型是由Keller和Segel在20世纪70年代提出的KS模型[1]，本文在KS模型的基础上，研究了文献[2]提出的描述老年痴呆症疾病中小神经胶质细胞集聚现象，以及文献[3]中给出的有关趋化过程中的群体效应的吸引-排斥趋化模型。从数学的角度来说，经典的KS模型和群体效应吸引-排斥趋化模型存在的一个本质区别，即前者可以找到有用的Lyapunov泛函，而后者一般不存在这样的泛函。

因此，本文考虑带有Logistic源的吸引-排斥趋化模型，如式(1)所示。

式中：Ω⊂Rn(n≥1)是一个光滑有界凸区域；∂ν表示边界∂Ω的外法向量的导数；χ，ζ，α1，α2，β1和β2均为给定的正参数；u=u(x，t)表示细胞的密度；v=v(x，t)表示吸引信号的浓度；w=w(x，t)表示排斥信号的浓度。f满足Logistic条件，即

f(s)≤as-bs2，s≥0

(2)

式中：a≥0，b>0。

模型(1)中第一个方程描述细胞密度随时间的变化情况，等式右边第一项表示细胞的随机扩散，第二项表示细胞向化学信号浓度增加的方向移动，第三项则表示细胞向远离化学信号浓度增大的地方迁移，最后一项表明细胞的出生和死亡满足Logistic定律。模型(1)中第二个和第三个方程表明趋化吸引和趋化排斥的化学物质均有细胞自身分泌，并随时间经历扩散和衰减。模型(1)中，假设u，v，w满足零流边界条件，即假设在边界处细胞和两种化学物质的净流量为零。

本文假设模型(1)初始值u0，v0，w0满足：

(3)

在一些研究KS数学模型的报道[4-5]中，发现趋化吸引和排斥现象同时存在，从而产生了有趣的生物斑图[6]。而文献[7]中带Logistic源的吸引-排斥趋化模型表明：当空间维数n≤2时，它存在唯一的整体古典解。因此本文的目标是：当n≥3时，证明模型(1)的整体古典解的存在性及有界性。更精确地说，本文获得如下主要结果。

定理1假设Ω⊂Rn(n≥1)是一个光滑有界凸区域，并设f满足式(2)，则对任意的u0，v0，w0满足式(3)，存在b0>0，使得当b>b0时，模型(1)存在唯一的非负古典解(u，v，w)，且u，v，w在Ω×(0， ∞)上一致有界。

本文先建立古典解的局部存在性并推导基本的先验估计，接下来再进一步推导解的更高正则性估计，完成定理1的证明。

1 局部存在性及基本估计

模型(1)的局部古典解的存在性建立在标准的不动点方法上[8]，这里省去其详细的证明过程。

引理1假设Ω⊂Rn(n≥1)是一个光滑有界的区域，并设f满足式(2)，且u0，v0，w0满足式(3)，则存在Tmax∈(0， ∞]和唯一的非负函数组(u，v，w)，且满足

使得(u，v，w)是模型(1)在Ω×(0，Tmax)上的古典解。进一步，则有

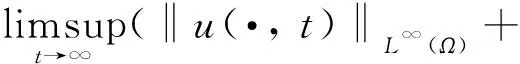
‖v(·，t)‖W1， k(Ω)+‖w(·，t)‖W1， k)=∞

引理2假设f满足式(2)，则存在常数A>0，使模型(1)的解(u，v，w)满足

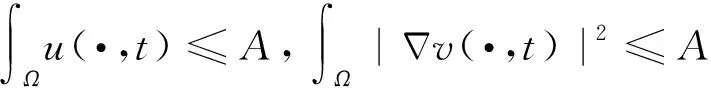
(4)

证明：根据模型(1)中第一个方程，并利用分部积分可得

(5)

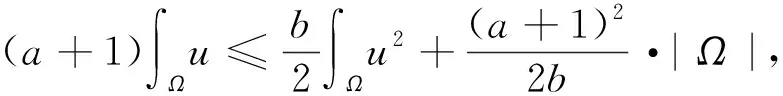
(6)

模型(1)中第二个方程两边同时乘以-Δv，并借助分部积分和Young不等式得

从而有

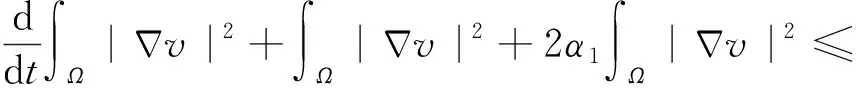
(7)

同理有

(8)

由此推得

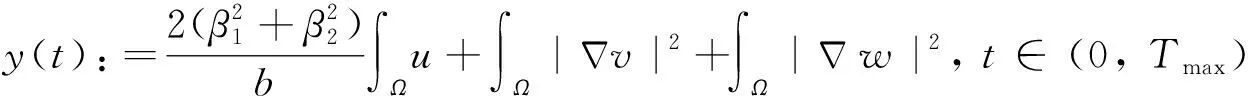
y′(t)+c1y(t)≤c2,t∈(0，Tmax)，

式得

结合y的定义，得出式(4)。从而引理2得证。

2 高阶正则性估计

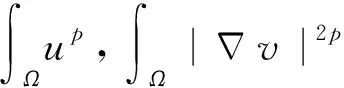
引理3假设f满足式(2)，则对于所有的p∈N和q∈{0， …，p}，成立

(9)

证明：直接计算得

(10)

由分部积分知

(11)

(12)

且

(13)

其中，t∈(0，Tmax)。接下来用Young不等式处理I4得

(14)

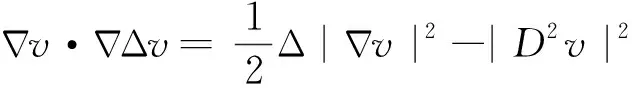
(15)

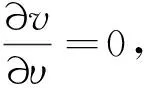
推论4假设f满足式(2)，则对于所有的p∈N和q∈{0， …，p}，成立

(16)

证明：根据引理3的证明方法， 类似推得

(17)

结合式(9)，即可推出式(16)，从而推论4得证。

项的估计。

引理5假设f满足式(2)，则对所有的p∈N，p≥2，存在c0>0和C0>0，使模型(1)的解具有下述性质

(18)

证明：式(16)中取q=0，利用分部积分和Young不等式得

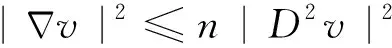
(19)

同理

(20)

引理6若p∈N，p≥3且引理1的假设成立，则存在常数C1使得模型(1)的解满足

(21)

证明：令式(16)中q=1得

：=I1+I2+I3+I4+I5，t∈(0，Tmax)

(22)

利用Young不等式估计得

(23)

(24)

(25)

(26)

其中，t∈(0，Tmax)。再次使用Young不等式估计式(26)的最后一项得

综合式(22)～(26)推出

(27)

同理可得

(28)

令

结合式(27)和(28)，即推出式(21)，从而引理6得证。

为了处理式(21)中的右端项，需要在式(16)中考察q≥2的情形且要对式(16)右端项作进一步的处理，更精确地说，有如下引理7。

引理7假设f满足式(2)，则对所有的p∈N，p≥3和每个q∈{2， …，p-1}，存在cq≥0和Cq≥0，使模型(1)的解满足

(29)

证明：利用Young不等式估计式(9)左边的第一项和最后一项得

(30)

(31)

再一次根据Young不等式得

(32)

其中，常数c′>0。同理有

(33)

(34)

(35)

(36)

其中，t∈(0，Tmax)。进一步由Young不等式得

(37)

(38)

(39)

(40)

综合式(9)和(30)～(40)得

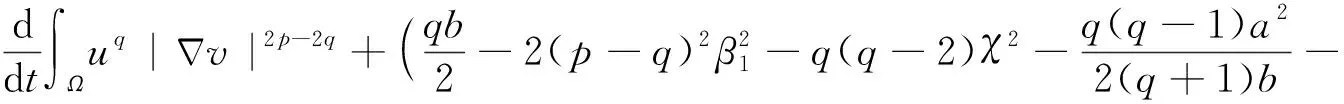
(41)

同理

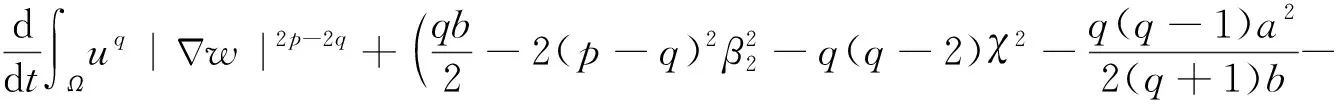
(42)

因此，由式(41)和(42)得式(29)，从而引理7得证。

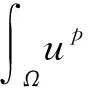
引理8假设f满足式(2)，则对所有的p∈N，p≥2， 存在cp和Cp使模型(1)的解满足

(43)

证明：式(16)中取p=q得

(44)

进一步根据Young不等式得

(45)

同理

(46)

再利用Young不等式得

(47)

综合式(45)～(47)得

(48)

由式(48)很容易得出式(43)，从而引理8得证。

为了能用引理5～8所得到的估计中“左端的好项”来控制“相应的右端的积分项”，将这些估计式进行合适的线性组合，得到如下引理9。

引理9假设p∈N，p≥3且引理1中假设成立，则存在b0=b0(a，b，χ，ζ，β1，β2，p，n)，对任意的b>b0(>0)，存在正数c，C及d0， …，dp，使模型(1)的解满足

(49)

证明：取c0， …，cp和C0， …，Cp是引理5～8中给出的常数， 同时取M≫1，使得

Mcq>2，q∈{2， …，p}

(50)

进一步， 选取0<ε≪1满足

(51)

且

(52)

固定b0>0，并使其充分大，满足

(53)

(54)

定义

d0：=1，dq：=εMq，q∈(1， …，p)

(55)

根据引理5～8， 在式(49)左边的求和项中，分别取q=0，q=1，q={2， …，p-1}及q=p，并经过重新排序得

(56)

联合式(51)～(55)得

(57)

再由式(52)和(53)得

(58)

进一步，根据式(54)及假设b>b0得

(59)

由于dqcq-dq-1=εMq-1(Mcq-1)>εMq-1>εM，q∈(2， …，p)且式(50)中M>1， 故有

(60)

类似推得

(61)

和

(62)

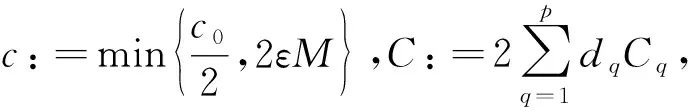
引理10假设p∈N，p≥3且引理9中的假设成立，则存在L>0，满足

(63)

证明： 对每个q∈{1， …，p-1}， 利用Young不等式得

(64)

(65)

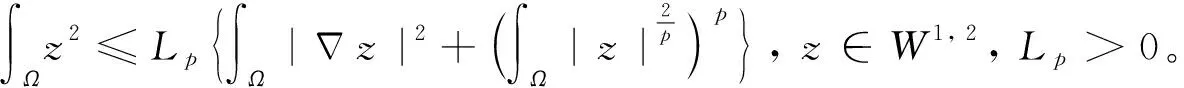
(66)

(67)

同理

(68)

其中，t∈(0，Tmax)。综合式(64)～(68)得

(69)

其中，L2>0和Lp>0。进一步，利用Young不等式得

(70)

据此便得到式(63)，从而引理10得证。

3 主要结果的证明

利用引理10中得到的高阶正则性先验估计，现在可完成定理1的证明。

定理1的证明：根据引理10及标准的Moser迭代可以得到：存在常数C>0，满足

‖u(·，t)‖L∞(Ω)≤C，t∈(0，Tmax)。

据此并结合引理10，由引理1得到Tmax=+∞，从而模型(1)的整体古典解存在有界性，即定理1证毕。