一种新型光学微腔的理论分析∗

谷红明 黄永清 王欢欢 武刚 段晓峰 刘凯 任晓敏

(北京邮电大学,信息光子学与光通信国家重点实验室,北京 100876)

(2018年1月10日收到;2018年3月21日收到修改稿)

应用波动光学理论,分析了一种新型锥顶柱状光学微腔的本征模式,得到了谐振腔的谐振波长表达式.在谐振波长1550 nm附近进行了设计与仿真优化,优化结果显示新型谐振腔与传统平行腔相比,在腔长为4512.5 nm,直径为3134.4 nm时,其品质因数可以提高22.4%,达到了49928.5,同时谐振腔的有效模式体积减小了47.8%.

1 引 言

随着激光技术的不断发展,高品质因数(Q)光学微腔受到了广泛关注,其应用不仅适用于传统光学领域,在量子信息和集成光电子芯片方面更是有着广阔的应用前景[1].单光子源是量子通信系统中的关键性器件,其可以通过量子点与光学微腔强耦合的方式得到.高Q值与小模式体积光学微腔的Purcell效应因子[2]较大,可以实现量子点与光学微腔的强耦合.

光学微腔结构多种多样,法布里-珀罗(F-P)型微腔是光学微腔的一种,其由两个平行放置的高反射镜组成,结构较为简单,在光学滤波器[3]、谐振腔增强型(RCE)光探测器等[4]光电子器件中已经得到了较为广泛的应用.柱状F-P型微腔有着较小的模式体积,可以应用于电抽运单光子发射[5].1999年,Yamamoto研究组的Kim等[6]采用柱状F-P型微腔,在温度50 mK下,首先实现了GaAs/AlGaAs量子阱三明治结构的单光子发射.近年来,国内在单光子发射方面也取得了较大进展.2013年,陆朝阳等[7]利用顶部5周期与底部24周期分布布拉格反射镜(DBR)结构的柱状微腔,提高了共振荧光的收集效率,实现了近似不可区分全同单光子源,其测量得到光子的相似度为0.97.为了提高F-P型柱状微腔的Q值,科研人员进行了深入研究.2005年,Forchel研究组Löffler等[8]在960 nm附近谐振波长处,实现了直径为4µm,Q值高达27700的微柱.2007年,Strauf等[9]采用预插入铝氧化物层的方法,对大尺寸DBR谐振腔进行挖孔,利用该孔洞对DBR中光场的限制,减少了普通柱状微腔表面的散射损耗,从而形成了高Q值(Q=50000)的微腔.与微盘谐振腔[10−12]类似,在F-P型柱状微腔中引入回音壁模式(WGMs)也可以增加柱状光学微腔的Q值,2012年,Albert等[13]采用直径为4.5µm,品质因数为40000的柱状微腔实现了量子点激光器WGMs的定向激射.

本文设计了一种新型非平行的锥顶柱状光学微腔,其结构特点是谐振腔顶部为锥面反射镜,底部为平面反射镜,顶部反射镜与底部反射镜之间构成腔体.理论分析表明,这种结构的光学谐振腔能够产生稳定的振荡,且能将光场有效地控制在腔内较窄的区域从而增加谐振腔的Q值并减小谐振腔的模式体积.本文分析了此种新型谐振腔的本征模式,采用COMSOL软件对腔体结构进行了仿真,仿真结果显示此种谐振腔与同等尺寸的F-P型微腔相比具有较高的Q值与较小的模式体积.

2 锥顶柱状谐振腔结构与基本原理

2.1 锥顶柱状谐振腔结构

图1为新型锥顶柱状谐振腔结构示意图及其轴线剖面图,由图1可见,新型谐振腔底镜是高反平面镜,记为M1;顶镜为高反锥面镜,记为M2;圆锥底角为α;腔长为H;腔内填充介质的折射率为n1;腔外介质的折射率为n2.

图1 (a)新型谐振腔结构示意图和(b)轴线剖面图Fig.1.(a)Schematic of a new asymmetric resonator structure and(b)resonator axial section.

2.2 锥顶柱状谐振腔谐振的基本原理

图2为新型谐振腔内光线传播示意图,图中A点处垂直于底部反射镜的入射光线经路径AB—BC—CD—DE(红色箭头所示),在顶部反射镜与底部反射镜各发生两次反射之后,再经ED—DC—CB—BA到达A点;类似地,任选一条由底部入射的光线(蓝色实线)在顶部反射镜的左侧和右侧各反射一次之后,垂直入射到底部反射镜,再由原路返回至初始位置,容易证明蓝色和红色实线所示的光束在折射率为n1的腔体中往返的总路程L0是相等的,均为L0=8H cos2α.因此,由反射镜M1与M2构成的腔体可以形成稳定的谐振.红色虚线所示为光线在顶部反射镜左侧和右侧各有一个交点的极限情况.经几何证明,线段可取得的最大值为2H sin(2α),此时A′点与E点重合于O点,令其为圆柱底面的半径,即b=2H sin(2α).

图2 谐振腔内光线传播示意图Fig.2.Schematic of light propagation in the resonant cavity.

3 理论分析

图1(a)所示的新型锥顶柱状谐振腔由图1(b)的剖面图沿轴线旋转得到,因此其谐振的场分布等特征与二维平面下的情况相类似.

在二维平面内谐振腔的偏振模式可以分为两类TE模与TM模,TE模(H波)非零向量为Ey,Hx和Hz,TM模(E波)非零向量为Hy,Ex和Ez.假定腔内填充各向同性的理想介质,其折射率为n1,谐振腔外围介质折射率为n2.将TE模(TM模)的电场(磁场)Ey(Hy)用Fy(x,z)表示,则光场的波动方程为

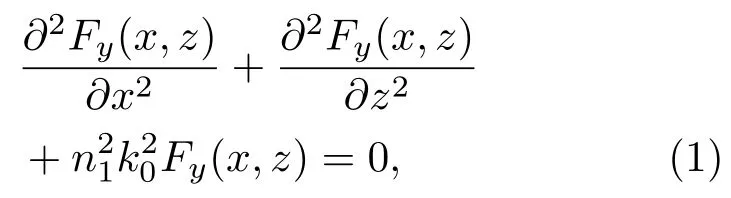
式中k0为真空中的传播常数.将谐振腔中折叠传播的光线展开,可以发现这种谐振腔可以等效为一个变形的介质矩形腔,其条宽为2b,等效腔长为L=L0/2.新型谐振腔的模式特征可以通过分析等效后的介质矩形谐振腔来得到.

介质矩形谐振腔即在介质波导的两端分别添加高反射率的反射镜,则在自然坐标系下沿光线传输方向的模场分布的一般形式为

式中km与βl分别为横向和纵向的传播常数,且有

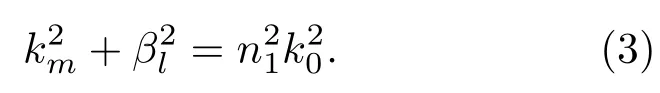
其横向可以看作对称的平板波导,其模式的本征值方程为

式中m为等效介质腔的横模数,φ12为边界的全反射位相角,大小为[14]

纵模方向主要受到高反射率镜的限制,可以得到纵模的本征值方程为

式中l为等效介质腔的纵模数;2φ为光线往返一周经过反射镜时总的反射相位角.设反射镜M1,M2反射相移为φj(θ),(j=1,2),其中θ为入射光线与反射镜的夹角.则总反射相位角大小为

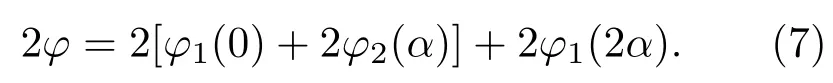
由(3)式、(4)式与(6)式可得谐振腔的谐振波长为

式中2b为谐振腔的宽度4Hsin(2α);L为等效介质腔的长度4Hcos2(α).

由(8)式可以看出,谐振腔的二维剖面下谐振波长表达式的形式与理想介质矩形腔的形式相同,因此新型锥顶柱状谐振腔可以等效为一个半径为b,腔长为L的圆柱形谐振腔.其谐振波长为

式中

其中µmn为m阶贝塞尔函数导数的第n个根,νmn为m阶贝塞尔函数的第n个根.

4 计算仿真

4.1 仿真结构参数

仿真时高反镜M1,M2采用DBR,反射率谱谱宽约为1µm,中心波长为λ0=1550 nm,其由4对Si/SiO2材料薄膜[15,16]构成,折射率分别为3.47与1.47,各单层膜的光学厚度分别为λ0/4.腔内的填充介质为硅,折射率为3.47,即n1=3.47,腔外为空气,折射率为1,即n2=1.选取谐振腔的横向与纵向尺寸均在微米量级,此时横向界面对谐振腔有较强的限制作用,因此2φ12=π.沿光传播方向的反射相移,可以由矩阵光学的方法来计算,令DBR的等效光学导纳γ=a(θ)+ib(θ),于是当衬底的光学导纳为实数,即衬底对入射光无吸收时,DBR反射镜的M1,M2的反射相移[17]为

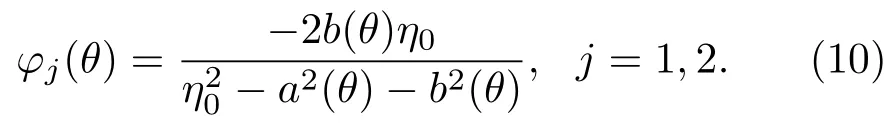
式中η0为斜入射时入射介质的光学导纳.对于λ0/4无吸收材料的光学薄膜,波长λ0处的等效导纳为实数,由(10)式可以计算出,在波长λ0处φj(θ)=0.在波长λ0附近谐振时,可以忽略DBR反射相移的影响,从而(8)式可以简化为

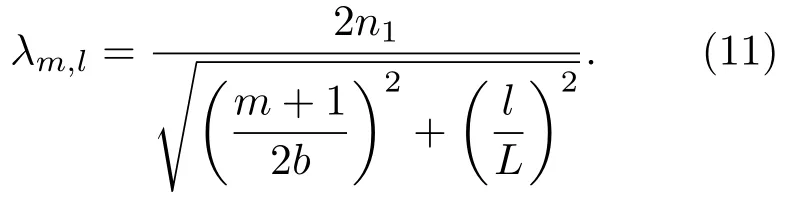
因此,要使谐振腔在中心波长处谐振,则简化后的腔长表达式为

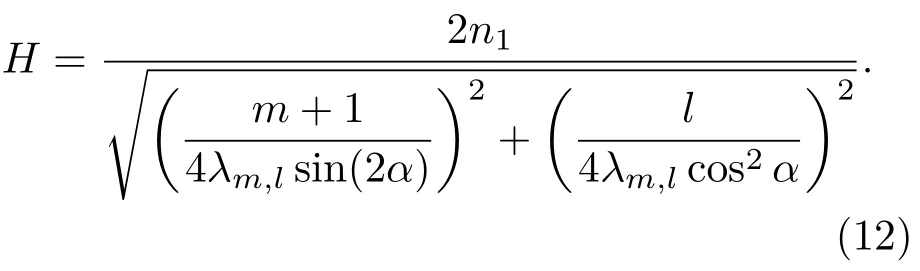
取m=0,l=80,α =3◦,当谐振腔在波长λ0处谐振,即λm,l=λ0时,通过(12)式可以计算出腔长H=4510.9 nm,2b=1886.1 nm.同理,可以计算出不同倾角α时,谐振腔的结构参数如表1所列.

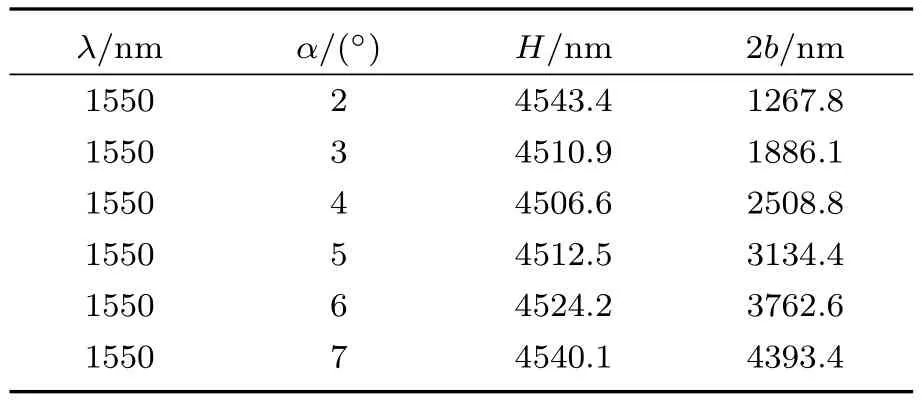
表1 不同倾角下谐振腔的结构参数Table1. Structural parameters of resonators with Different angles.

4.2 仿真结果

4.2.1 宽谱扫描

对角度为3◦的仿真结构进行了宽谱扫描,扫描的能量谱如图3所示.

谐振腔Q值的计算公式为

式中f0为谐振中心波长;∆f为谐振峰的半高全宽(FWHM).通过(13)式计算TE偏振下,倾角为3◦谐振腔的Q值如表2所列.

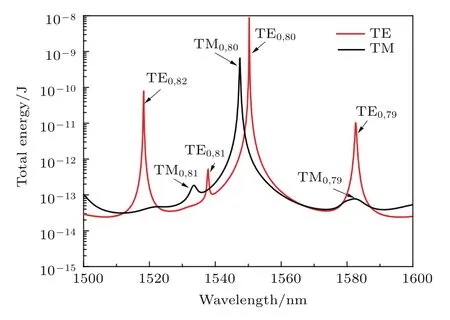
图3 不同入射波长时谐振腔的能量谱(α=3◦)Fig.3.Energy spectra of resonators with Different incident wavelengths(α =3◦).

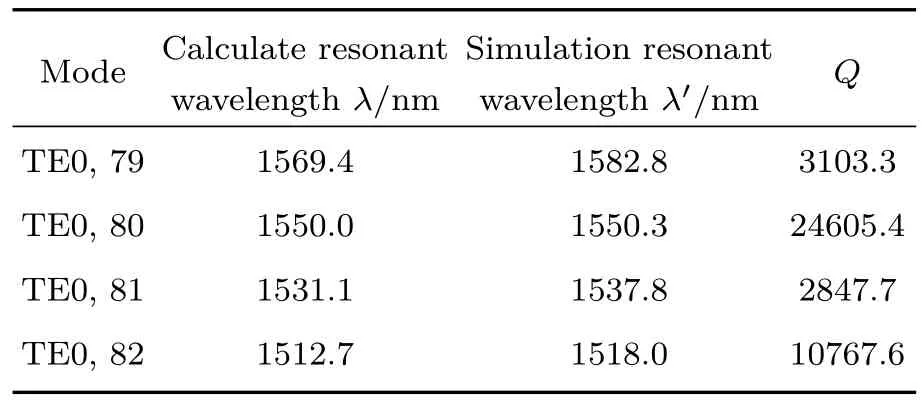
表2 倾角为3◦时,TE偏振光下谐振腔的Q值Table2.Q values of asymmetric resonator under TE polarized light at an angle of 3◦.

4.2.2 不同角度α下的扫描

对于谐振波长为1550 nm的TE0,80谐振模式,通过改变顶镜圆锥底角α (α =2◦,3◦,4◦,5◦,6◦,7◦),探究了顶镜倾角变化对谐振腔Q值的影响.图4为不同圆锥底角下谐振腔TE0,80模的谐振能量谱.图5为TE0,80谐振模式的Q值随圆锥底角α变化的折线图.

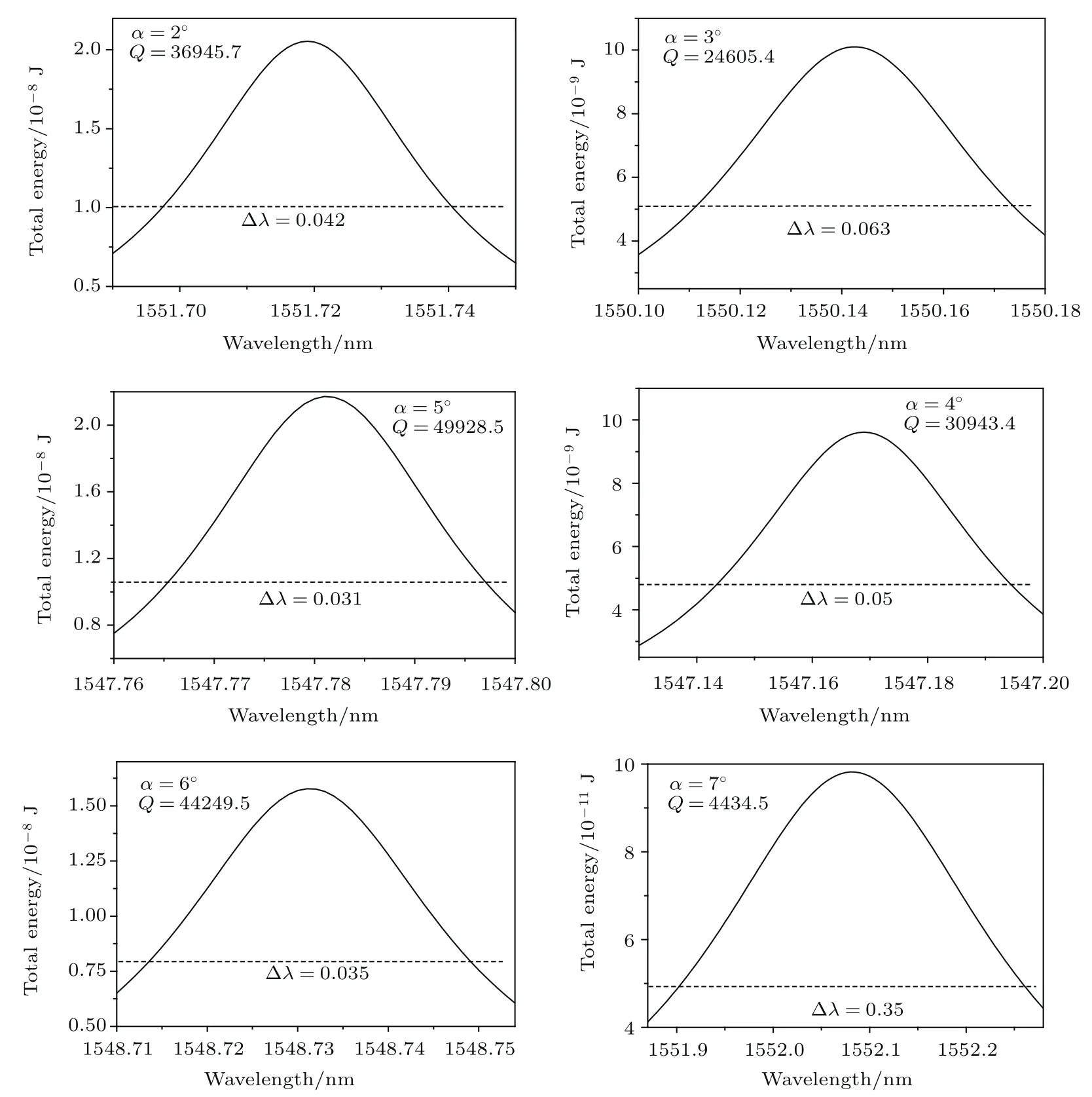
图4 不同圆锥底角下谐振腔TE0,80模的谐振能量谱Fig.4.Resonance energy spectra of TE0,80mode in Different cavity with Different angle.

图5 TE0,80谐振模式的Q值随顶镜圆锥底角的变化Fig.5.Q value of TE0,80mode changes with the cone bottom angle.

4.2.3 有效模式体积与场分布

有效模式体积是微型谐振腔的重要参数之一.有效模式体积的定义为

式中ε(r)为介电常数;E(r)为腔内光场的电场分布.

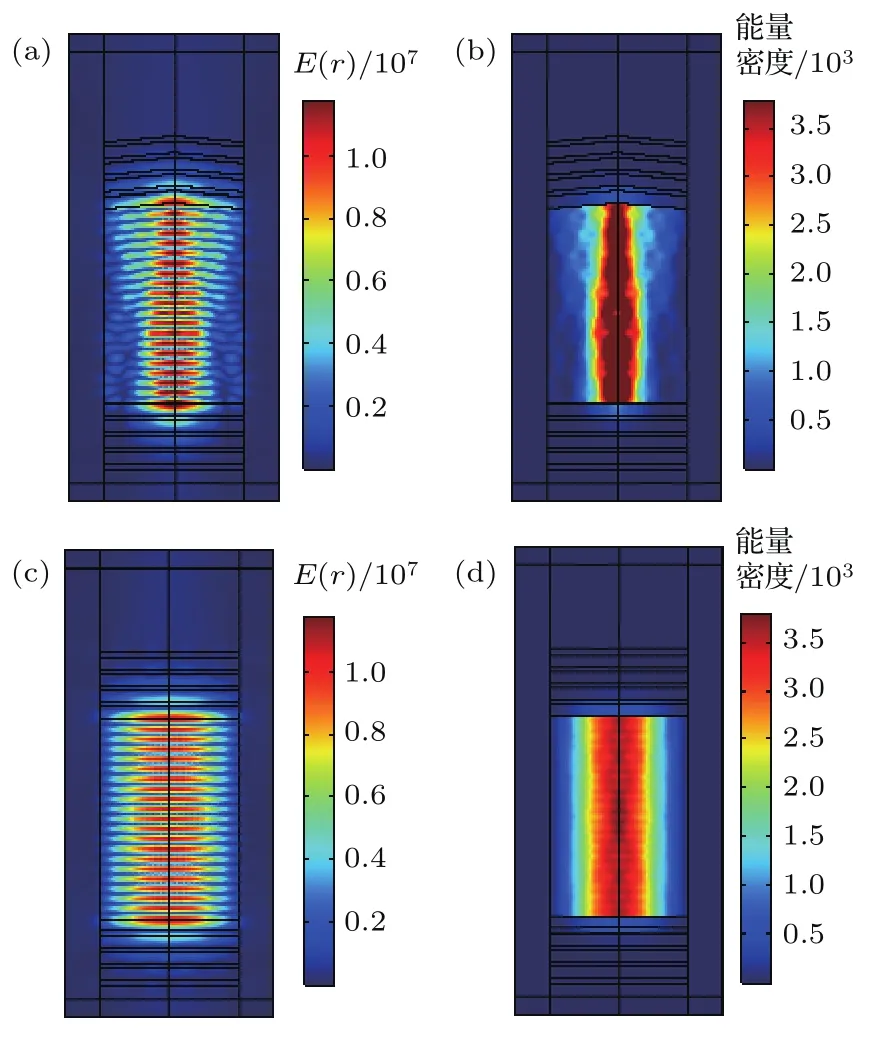
图6 倾角5◦,谐振波长1547.781 nm时,谐振腔内的电场分布(a)和能量密度分布(b);同尺寸下谐振波长1549.763 nm时,平行谐振腔内的电场分布(c)和能量密度分布(d)Fig.6.Electric field distribution(a)and energy density distribution(b)when inclination angle is 5◦and resonance wavelength is 1547.781 nm;electric field distribution(c)and energy density distribution(d)for the same size of the parallel resonant when wavelength is 1549.763 nm.

针对角度优化的结构,将倾角为5◦时新型谐振腔的模式体积与相同尺寸矩形腔的作对比.设谐振腔的厚度为∆d0.对于填充各项同性介质的谐振腔,(14)式可以变形为

图6展示了倾角为5◦与同等尺寸平腔时,腔内的电场分布与能量密度分布.

5 讨论分析

由图3可以看出新型谐振腔在短波长处的自由谱域比长波长处的要窄,这主要是由提出的锥顶柱状微腔为介质谐振腔存在频谱浓缩[18]导致的.对比表1与图3中的谐振波长可以发现,通过(11)式计算TE0,80与TM0,80模式处的谐振波长与仿真的谐振波长较为符合分别为1550.2 nm和1547.4 nm.而且可以看出TE0,80与TM0,80的谐振波长并不完全重合,这是由于简化后的(11)式未考虑横向边界对偏振的影响而导致的.由于通过(11)式计算时也未考虑DBR色散的影响,因此计算其他远离中心波长模式的谐振波长与仿真的谐振波长有略微的偏差,DBR的色散偏差导致边模谐振波长偏移8 nm左右.

图5为TE0,80谐振模式的Q值随圆锥底角α变化的折线图,由图5可以看出对于DBR中心波长1550 nm的谐振腔,在倾角α为5◦附近TE0,80谐振模式的Q值取得扫描范围内的最大值.此时线宽为0.031 nm,通过(13)式计算的Q值为49928.5,同尺寸的介质矩形腔的线宽为0.038 nm,Q值为40783.2,由此可以看出Q值提高了22.4%.而且,可以看到当圆锥底角增大到7◦时,主要由于DBR的倾角较大造成其反射率下降[19],从而谐振腔的Q值出现了较大的下降.

图6为倾角5◦的新型谐振腔与同等尺寸平腔腔内的电场分布与能量密度分布,对比图6(b)与图6(d)可以定性看出图6(b)的能量分布较为集中.通过(15)式计算可得图6(b)的模式体积为3.5µm2·∆d0,图6(d)的模式体积为6.7µm2·∆d0.也就是说,倾角为5◦的新型谐振腔的模式体积与传统平腔的模式体积减小了47.8%.

高Q值与小模式体积的微腔在单光子发射方面有着广泛的应用.另外,在微粒探测以及生物大分子检测等方面,高Q值微腔同样发挥着较大的作用.在以往利用动态掩膜湿法腐蚀制作一镜斜置三镜腔光探测器[20,21]的过程中,曾对不同角度斜面镜的制作有着较为深入的研究,因此新型锥顶柱状光学微腔在制备方面有着较好的可行性.

6 结 论

应用波动光学理论,分析了锥顶柱状光学微腔的本征模式,得到了谐振腔的谐振波长表达式.并应用COMSOL软件采用有限元的方法,对不同倾角DBR反射镜构成的谐振腔结构进行了仿真,仿真的谐振波长与求解出的基本符合.另外,对谐振腔的倾角进行了仿真优化,优化结果显示在扫描范围内对于谐振腔的TE0,80模式,当倾角为5◦,即腔长为4512.5 nm,直径为3134.4 nm时,谐振腔的品质因数最大,达到49928.5.最后,将新型谐振腔在5◦倾角时的结构与同等尺寸下平腔进行了对比,结果显示新型谐振腔的Q值提高了22.4%,同时模式体积减小了47.8%.