采用衍射掩模产生白光横向平顶光束∗
陈芳萍 张晓婷 刘楚嘉 漆宇 庄其仁
(华侨大学信息科学与工程学院,福建省光传输与变换重点实验室,厦门 361021)
(2018年1月4日收到;2018年3月21日收到修改稿)
白光横向平顶光束在定向背光式自由立体显示器中有重要应用.本文提出一种采用带蝶形小孔阵列的衍射掩模片获得白光横向平顶光束的方法.根据广义惠更斯-菲涅耳衍射积分和多波长叠加原理,推导出光强分布计算式.设计一套实验装置,数值模拟并实验验证出射光束在不同距离的横向光强分布以及小孔蝶形凹度(蝶形中心高度与边长的比值)对横向光强分布的影响.结果表明:当选择小孔蝶形凹度为0.50—0.66时,可以得到平顶因子F>0.89的白光横向平顶光束,横向平顶光束的宽度随着传输距离的增大而增大,而平顶因子基本不变.实验还发现柱面透镜的折射色散和衍射色散可以互相抵消,使白光横向平顶光束基本无色散.
1 引 言
在自由立体显示技术中,基于时间复用技术的定向背光自由立体显示能实现全分辨率、低串扰立体显示[1−6],是自由立体显示技术的一个重要发展方向.但传统定向背光白光光束的空间强度分布呈高斯分布,导致观看区域亮度分布不均匀,严重影响视觉舒适度,因此需要将定向背光白光光束整形为横向平顶光束[7].在现有的平顶光束研究与应用中,主要是针对激光光束的整形.激光光束整形方法有光阑拦截法[8]、相位型光束整形法[9]、微透镜阵列整形法[10]、二元光学元件衍射法[11]、液晶空间光调制器法[12]、离焦望远镜系统合成法[13]、超高斯反射镜腔[14]和非球面透镜组法[15]等.由于液晶显示器(LCD)背光源为白光面光源,与激光光源完全不同,因此这些用于激光高斯光束整形的方法不能直接用于定向背光白光光束整形.近年来,光束整形文献的研究兴趣集中在用光束合成的方法来产生和模拟平顶光束,相继提出了用偏心高斯光束叠加、多束高斯光束叠加和复宗量拉盖尔-高斯光束叠加等[16−18]模拟平顶光束的新方法.本文基于衍射积分和多波长叠加原理,提出采用带蝶形小孔阵列的衍射掩模片获得白光横向平顶光束的新方法.
采用衍射掩模和柱面透镜获得白光横向平顶光束的方法是在LCD背光源表面覆盖一层衍射掩模片,光场经过柱面透镜变换成为白光横向平顶光束.根据广义惠更斯-菲涅耳衍射积分理论分析柱面透镜出射光场的分布特性,通过数值模拟进行参数优化,并由实验装置进行验证.该方法结构简单,易于实现,为基于时间复用技术的定向背光自由立体显示提供一种新的白光平顶光束实现途径.
2 理论模型
衍射掩模产生横向平顶光束原理如图1所示.在LCD背光源的出光面覆盖一个衍射掩模片,衍射掩模片在竖直方向整齐紧密排列着蝶形小孔,蝶形小孔结构如图1(b)所示.蝶形小孔高度和宽度相等,均为h.定义小孔蝶形凹度β为中心高度a与h的比值,即β=a/h.在衍射掩模片前无间隙放置一个平凸柱面透镜,LCD背光源均匀光场经衍射掩模和柱面透镜变换为白光横向平顶光束投射到接收屏进行检测.
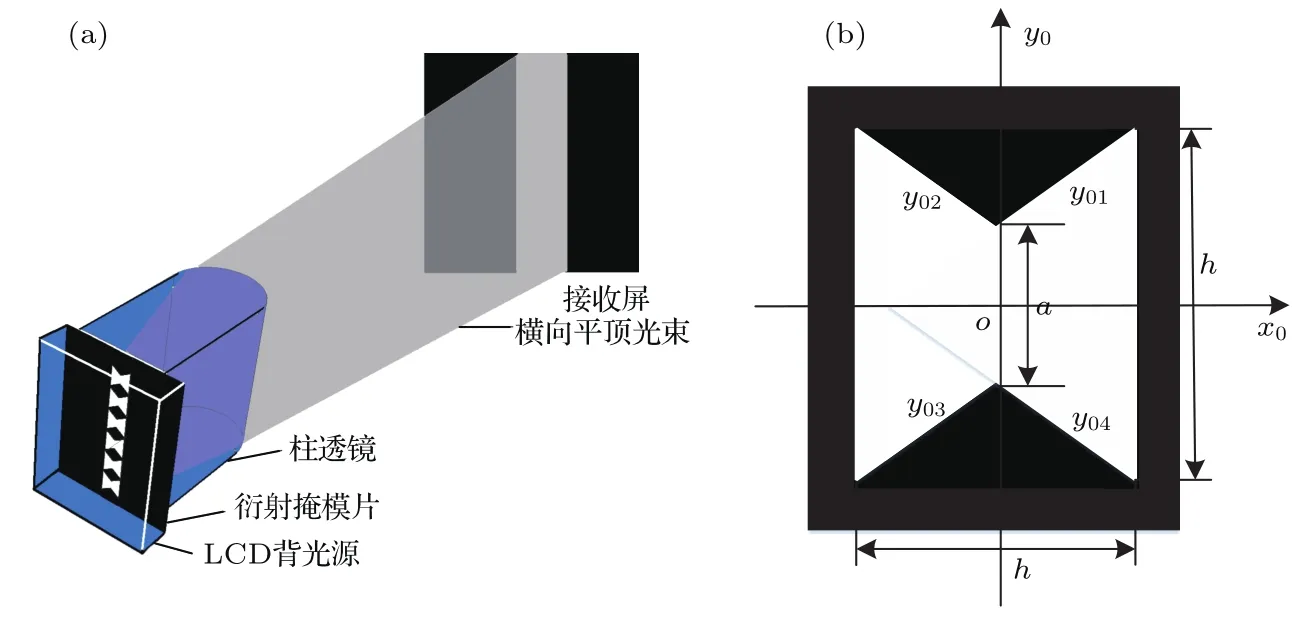
图1 (a)衍射掩模产生横向平顶光束原理图;(b)蝶形小孔结构Fig.1.(a)Schematic diagram of diffraction mask for generating horizontal flat-topped beams;(b)structural of butter fly-shaped holes.
柱面透镜结构剖面图如图2所示.图中d0为平凸柱面透镜的中心厚度,b为柱面透镜单元宽度.设x1处平凸柱面透镜的厚度为d(x1),则柱面透镜的透过率函数为
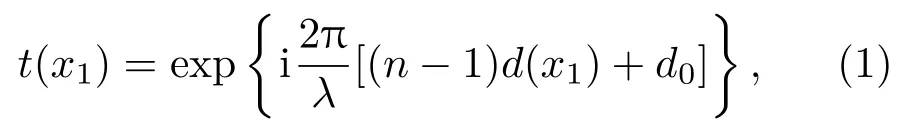
式中n为柱面透镜折射率.根据图2的几何关系可知
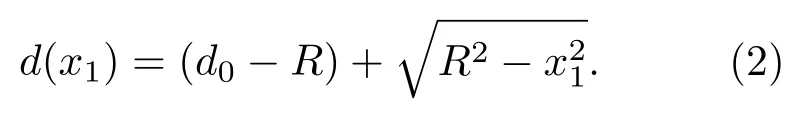
将(2)式代入(1)式并整理得

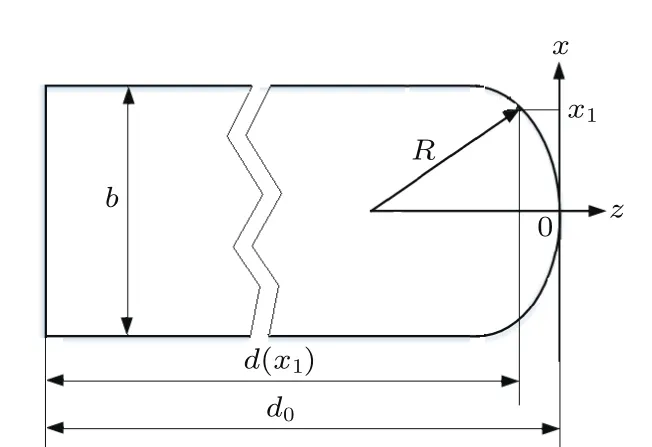
图2 柱面透镜的结构参数Fig.2.Structural parameters of the cylindrical lens.
根据广义惠更斯-菲涅耳衍射积分公式,波长为λ的光波在z=0平面的衍射光场可写为

式中m表示第m个蝶形单元,um0(x0,y0,λ)为衍射掩模平面的光场复振幅分布函数,由于衍射掩模片紧贴LCD背光源均匀发光面,可认为衍射掩模与光源在同一个平面,衍射掩模起到了改变光源发光面形状的作用,因此(4)式中面积元dx0dy0的积分面积Sm为蝶形的两个直边x0=−h/2,x0=h/2以及4个斜边y01,y02,y03,y04围成的面积,积分限分别为:

考虑到LCD背光源白光光谱宽度大,柱面透镜材料的折射率不是常数,而是波长的函数n=n(λ),可由Sellmeier色散公式表示为
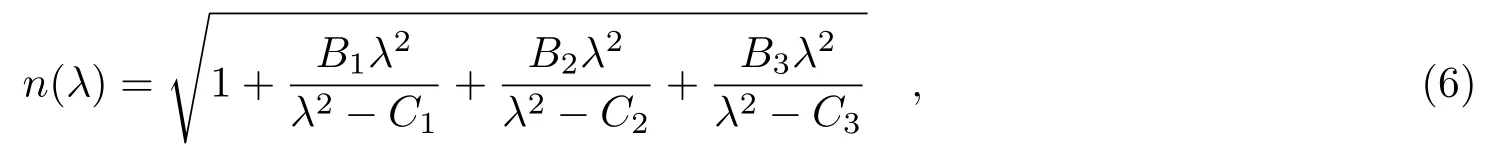
式中B1,B2,B3和C1,C2,C3为柱面透镜材料系数.将接收屏放置在z=z2处,可得接收屏上的单波长衍射光场为:

由于LCD背光源为白光光源,不同波长的光为非相干光,所以接收屏上的光强度分布等于各波长衍射光强度的线性叠加[19].通过测量光源的光谱强度分布,再按一定波长间隔取不同波长λl代入(7)式计算衍射光强度分布,可得到接收屏上的总光强分布为

式中cl为白光光源光谱中λl的相对强度值.
接收屏上的光强分布横向平顶特性可用平顶因子F来衡量[20],公式为
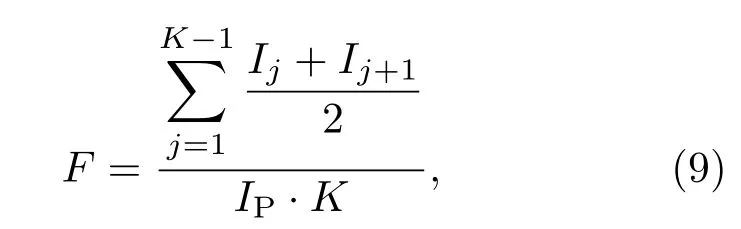
其中Ij为大于设定阈值的光强,IP为峰值光强,K为光强大于阈值的分割份数,阈值通常取半峰值高度.F值越大(0 6 F 6 1),白光横向平顶光束的平顶度越好.
3 数值模拟
首先采用光谱仪测量实验所用正白光发光二极管(LED)光源的光谱相对强度,如图3所示.LED白光光谱为连续光谱,数值模拟时将光源光谱按∆λ=10 nm波长等间隔取样,由图3曲线数据可得到各波长对应的相对强度值cl.
数值模拟采用的基本参数为:蝶形单元宽度h=50µm,小孔蝶形凹度β=0.4;柱面透镜宽度b=1.411 mm,柱面透镜曲率半径R=2.67 mm,柱面透镜厚度d0=8 mm(近似等于柱面透镜的焦距);柱面透镜材料为聚甲基丙烯酸甲酯(PMMA),根据文献[19]计算得到PMMA的Sellmeier色散公式材料系数见表1;光源波长λl取值范围400—700 nm,按(8)式进行数值模拟.
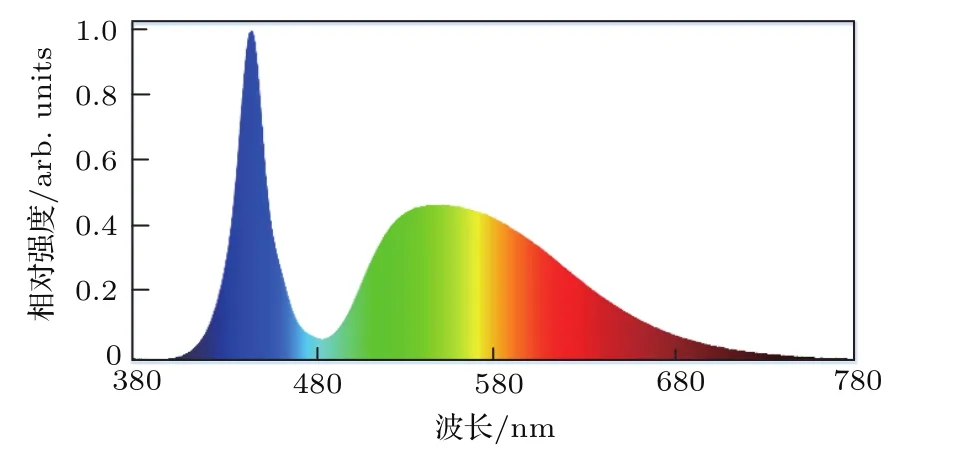
图3 白光LED的光谱相对强度分布曲线Fig.3.Relative spectral strength distribution curve of white LED.

表1 PMMA的Sellmeier色散公式材料系数Table1.PMMA material coefficient of Sellmeier dispersion formula.
改变接收屏与柱面透镜出射面距离为z2=500,1000,1500 mm和2000 mm,数值模拟得到接收屏横向白光光强分布曲线如图4所示.可以看到它们的光强分布曲线形状基本一致,采用(9)式计算平顶因子F,结果表明传播距离不改变横向白光光强分布的平顶特性(F≈0.89),如图6(a)示.随着传播距离的增大,平顶光束的横向宽度随着增大.这是由于掩模片的蝶形小孔有一定宽度,因此小孔出射光束经过柱透镜变换后不是理想的横向准直光束,存在一定发散角.对于平顶光束,其半高
全宽(FWHM)发散角可近似表示为θ1≈h/(d0−R),代入相关参数可得θ1≈0.00938.另外柱透镜出射光束属于细光束,衍射效应比较明显.衍射发散角θ2可近似表示为θ2≈ 2λ/b1,可得波长650 nm的红光衍射发散角θ2≈ 0.00093.因θ1和θ2为独立变量,都会使横向平顶光束发散,所以平顶光束横向宽度FWHM将随着传播距离的增大而增大.
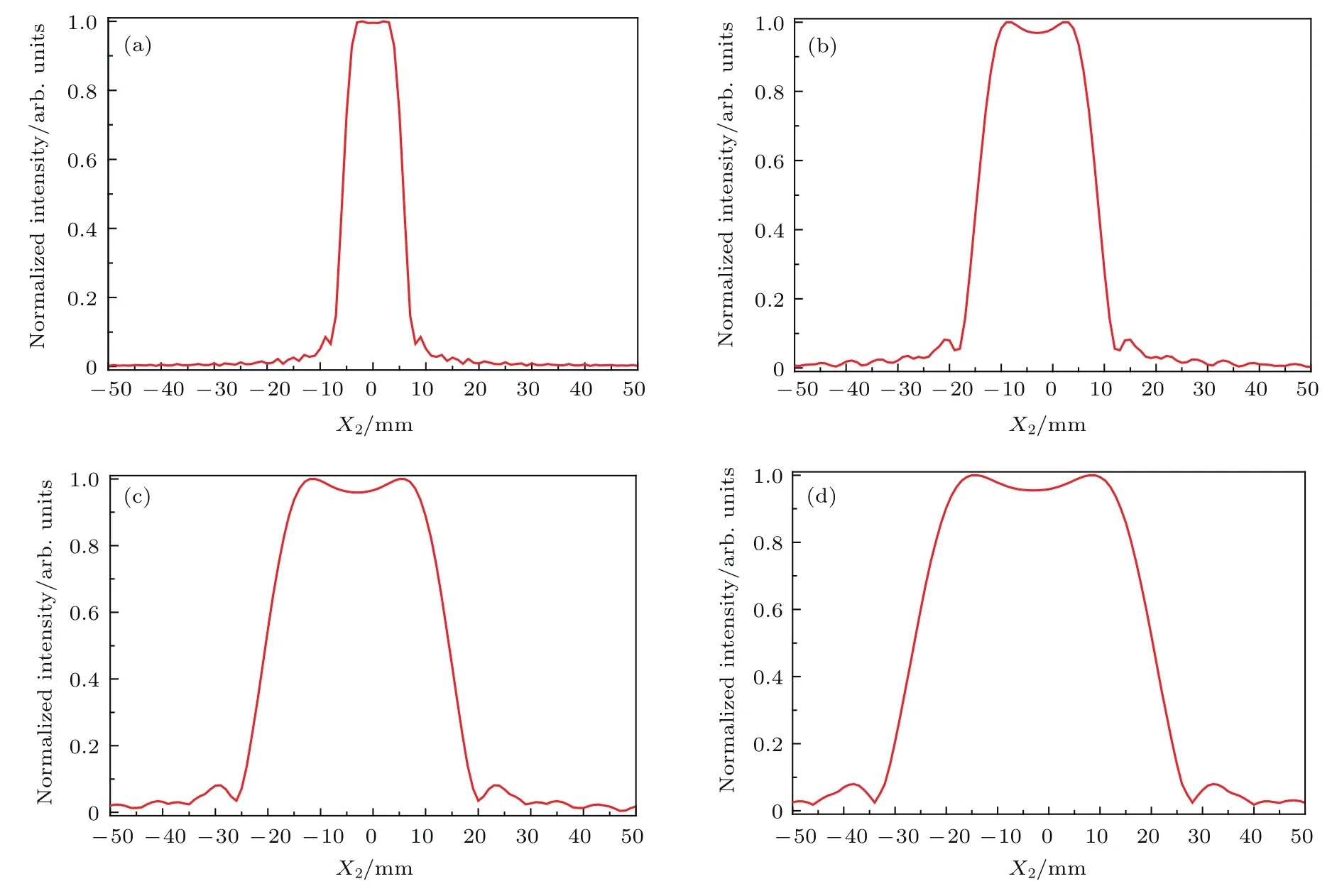
图4 数值模拟得到的接收屏横向白光光强分布曲线随距离z2的变化 (a)z2=500 mm;(b)z2=1000 mm;(c)z2=1500 mm;(d)z2=2000 mm.Fig.4.Simulated distribution curves of the horizontal white light intensity on the receiving screen vs.the distance z2:(a)z2=500 mm;(b)z2=1000 mm;(c)z2=1500 mm;(d)z2=2000 mm.
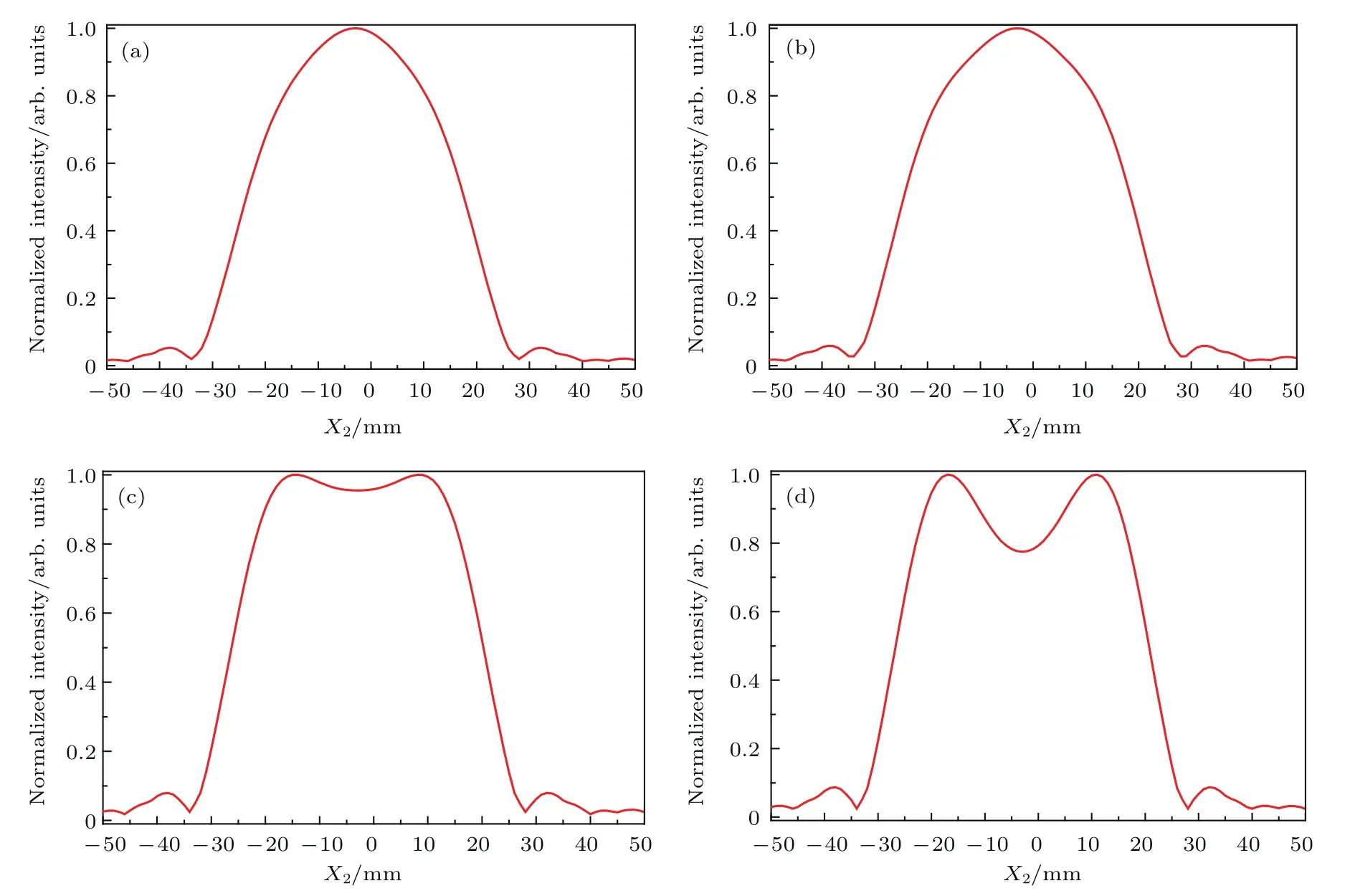
图5 数值模拟得到的横向光强分布曲线随小孔蝶形凹度β的变化 (a)β=1.0;(b)β=0.8;(c)β=0.6;(d)β=0.4Fig.5.Simulated distribution curves of the horizontal light intensity vs.the concavity of butter fly-shaped hole:(a)β=1.0;(b)β=0.8;(c)β=0.6;(d)β=0.4.
将接收屏与柱面透镜出射面距离固定为z2=2000 mm,改变小孔蝶形凹度β值,其余初始参数不变,数值模拟得到接收屏横向白光光强分布曲线如图5所示.图5(a)为β=1的光强分布曲线,此时蝶形小孔为正方形,可以看到接收屏横向白光光强分布曲线接近为高斯分布.图5(a)—(d)的光强分布曲线显示,小孔蝶形凹度β减小,光强分布曲线形状由高斯型向平顶型演变.同时可以看到,β=0.6的横向光强分布曲线比β=0.4的顶部更为平坦,平顶因子值更大,前者F=0.892,后者F=0.890,说明β值太小反而会降低平顶因子值.小孔蝶形凹度对柱透镜输出横向光强的影响主要来自小孔纵向衍射的叠加,小孔出射光束经柱透镜变换在纵向上与自由空间菲涅耳衍射基本相同.当蝶形小孔在纵向排成一个阵列时,就可以看成一个特殊结构的单缝.由于每个小孔的中心高度小于两边的高度,因此透过特殊单缝的光场中心能量密度小于两边的能量密度.经过一定衍射距离后,这种光场能量分布的不均匀使单缝衍射的光场能量分布特性发生改变,出现横向衍射光场中心能量下降的趋势.小孔蝶形凹度值越小,光场中心能量下降越明显,横向光强分布曲线越平坦,平顶因子F值越大.但当小孔蝶形凹度值小于一定值时,光场中心能量下降太多而出现中心明显凹陷,平顶因子F值反而下降,因此存在一个最佳小孔蝶形凹度使F达到最大值,如图5(c)所示.为了找出最优的β取值,模拟计算了平顶因子F随不同蝶形凹度β的变化规律,如图6(b)所示,图中二次拟合曲线显示β=0.5时平顶因子达到最大值F=0.894.由于β=0.4—0.6之间F的变化量很小(<0.5%),所以β取值从0.4—0.6都能得到很好的横向平顶光束.
上述模拟结果说明,当柱面透镜曲率半径和材料确定后,选择合适的小孔蝶形凹度β,可以将LCD背光源均匀光场经过衍射掩模和柱面透镜变换为横向平顶光束,横向平顶光束的宽度随着传输距离的增大而增大,且平顶因子基本不变.
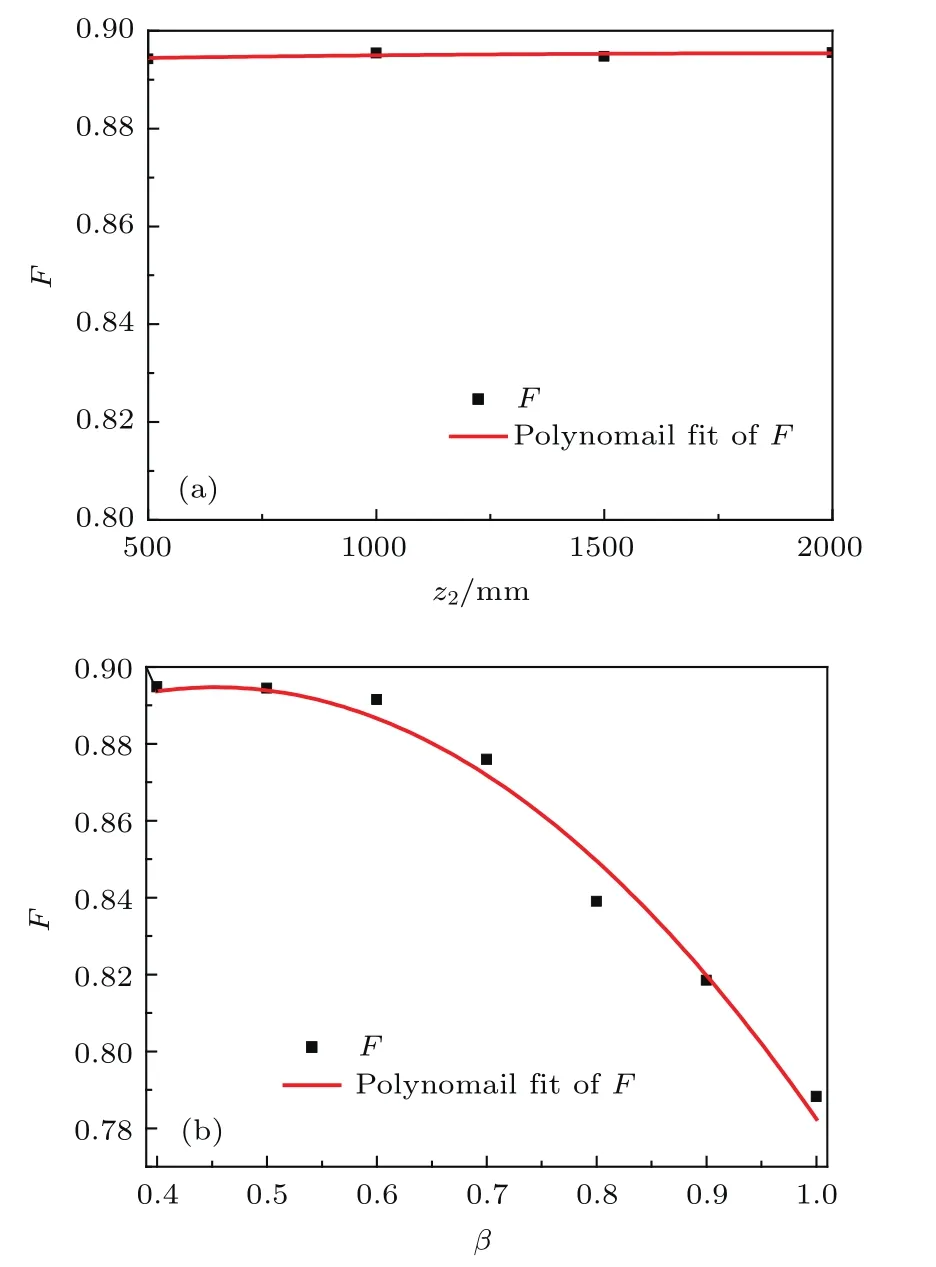
图6 模拟计算得到的平顶因子F随距离z2(a)和蝶形凹度β(b)的变化Fig.6. Simulated top- flat factor as a function of distance of dissemination z2(a),and concavity of butter fly-shaped hole β(b).
4 实验结果与分析
4.1 实验结果
实验装置如图7所示.其中柱面透镜采用PMMA柱面透镜光栅板,厚度d0=8 mm,光栅密度18线/英寸(即柱面透镜宽度b=1.411 mm),柱面透镜曲率半径R=2.67 mm.为了获得足够强度的均匀背光源,实验中将单只功率为3 W的正白光LED阵列放置于扩散板后面,组成直下式平板灯结构,代替LCD背光源.实验掩模板的制备采用菲林输出技术,先把小孔蝶形阵列经过栅格图像处理器(RIP)处理成点阵图像,利用激光菲林机使菲林片相应部位曝光,再通过显影机的显定影过程,把未曝光部分冲洗掉,就在菲林片上形成小孔蝶形阵列.菲林机最大分辨率2880 dpi,最小网格间距8µm,因此实际加工后的掩模板小孔蝶形参数为:高48µm,宽48µm,小孔蝶形凹度β=1,β=0.83,β=0.66和β=0.50.接收屏为漫反射的白屏,屏上的亮度分布与光束的强度分布成正比,因此可以用数码相机拍照并进行数据处理获得归一化光强度分布曲线.

图7 实验装置原理图Fig.7.Experimental setup.
图8为接收屏上白光光斑图样的数码相机照片及横向光强分布曲线.其中图8(a)—(d)分别对应蝶形凹度β=1.00,β=0.83,β=0.66和β=0.50的横向白光光强分布图.对图8数据按(9)式计算平顶因子F,得到接收屏上的实验光强分布图平顶因子F随蝶形凹度的变化规律如图9(b)所示.可以看到随着β值的减小,光强分布曲线从高斯型向平顶型的转变.β=0.50时横向白光光强分布平顶因子F达到最大值F=0.89.比较图5和图8可以看到,当蝶形凹度β=1.00和β=0.83时横向白光光强分布曲线呈现高斯型分布,而当β值减小为β=0.66和β=0.50时,光强分布曲线出现明显的平顶特征,说明实验结果与模拟计算结果符合.

图8 实验得到的横向光强分布曲线随小孔蝶形凹度β的变化 (a)β=1.00;(b)β=0.83;(c)β=0.66;(d)β=0.50Fig.8.Experimental horizontal light intensity distribution vs.the concavity of butter fly-shaped hole:(a)β=1.00;(b)β=0.83;(c)β=0.66;(d)β=0.50.
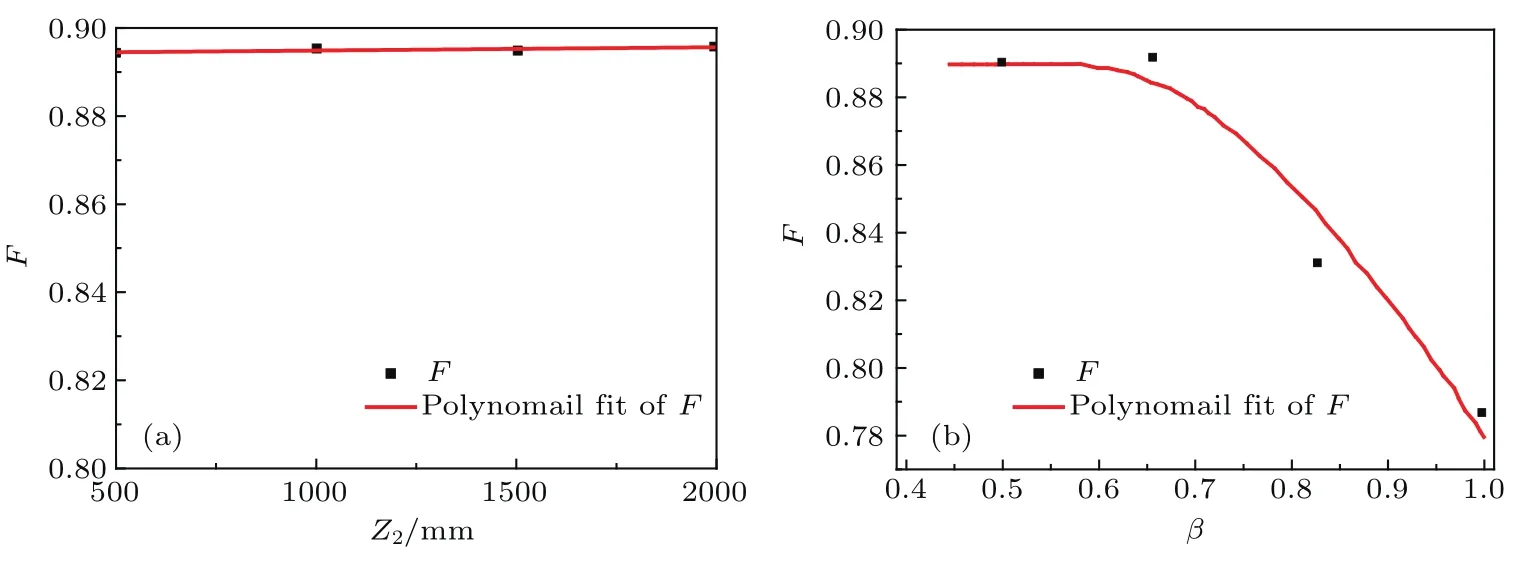
图9 实验得到的平顶因子F随距离z2(a)和蝶形凹度β(b)的变化Fig.9.Experimental top- flat factor as a function of distance of dissemination z2(a)and concavity of butter flyshaped hole β(b).
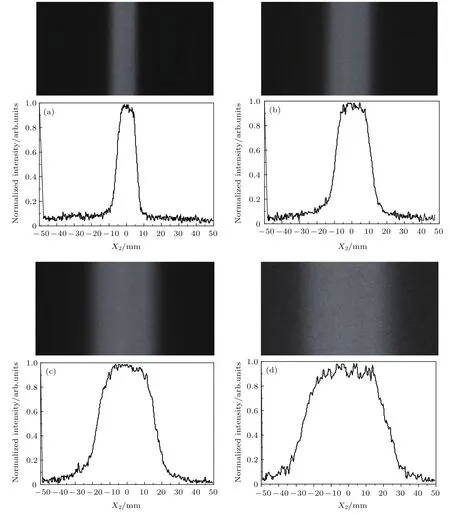
图10 实验得到的横向光强分布曲线随传播距离z2的变化 (a)z2=500 mm;(b)z2=1000 mm;(c)z2=1500 mm;(d)z2=2000 mmFig.10.Experimental horizontal light intensity distribution vs.the distance of dissemination:(a)z2=500 mm;(b)z2=1000 mm;(c)z2=1500 mm;(d)z2=2000 mm.
根据范西特-泽尼克定理[21],一个扩展不相干准单色光源在离它距离为z的受照面上可产生一个近乎完全相干的照明区,其直径为

图10为β=0.5,接收屏与柱面透镜出射面距离z2=500,1000,1500 mm和2000 mm时,实验得到的接收屏上白光光斑图样和横向光强分布曲线.可以看到横向光强分布曲线的平顶特性基本不随传播距离的变化而变化,经计算可知图10(a)—(d)的平顶因子F均大于0.89,如图9(a)曲线.比较图4和图10可知传播距离不改变横向白光光强分布的平顶特性,实验结果与数值模拟结果相一致.
4.2 色散对轴上平顶光束的影响
由于柱面透镜折射光束发散角和衍射光束发散角都是波长的函数,两者都会引起白光横向平顶光束的色散.图11给出了β=0.5,接收屏与柱面透镜出射面距离z2=500,1000,1500 mm和2000 mm时,实验得到的接收屏上红绿蓝(RGB)三基色光强度分布曲线.这里三基色是采用BMP图形文件格式存储的RGB数据进行处理的,将数码相机拍摄的接收屏照片通过图像分析软件Image Analyzer分析得到光强度分布曲线.可以看到图11(a)—(d)的RGB三基色光强度都具有平顶分布特性,且两边沿RGB三基色基本是重合的,即没有产生色散现象.这是因为柱面透镜折射率随波长增大而减小,蝶形小孔出射光束经柱面透镜圆柱面折射后引起的光束发散角随波长增大而减小(透镜色差);而衍射引起的光束发散角刚好与之相反,衍射光束发散角随波长增大而增大,两者相互抵消,结果降低了波长对横向平顶光束发散角的影响.根据几何光学原理和图2柱面透镜结构参数,求得柱面透镜圆柱面折射光线与光轴的夹角:
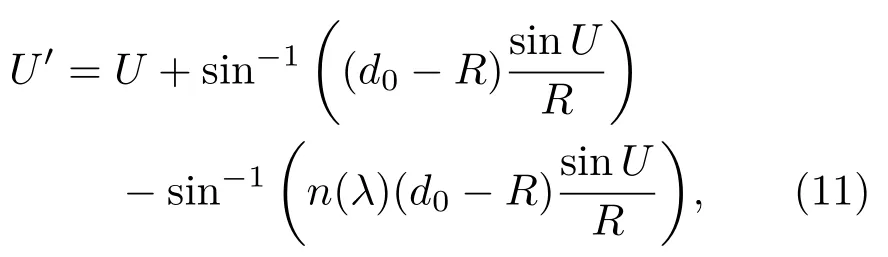
式中U为圆柱面入射光线与光轴的夹角,其值为负值.(11)式对波长求导数可得U′随波长的变化率:
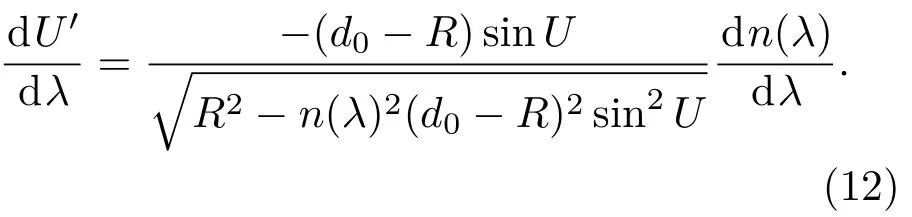
(12)式说明柱面透镜圆柱面折射光线与光轴夹角U′随波长的变化率(色散特性)与柱面透镜折射率随波长的变化率成负比例关系,将(6)式和柱面透镜参数代入(12)式可求得具体色散角度值.
柱面透镜出射平行光束的发散角θ(λ)可近似由夫琅和费衍射公式表示为
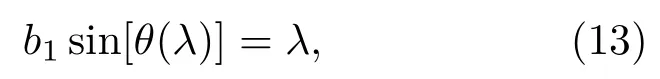
式中b1为柱面透镜实际出射光束宽度,则衍射发散角随波长的变化率为
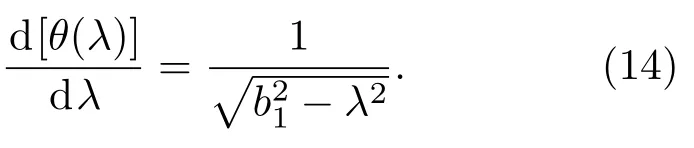
(14)式表明衍射光束发散角随波长增大而增大,当
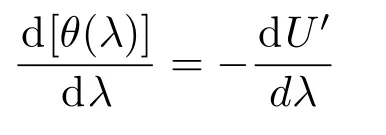
时,可消除折射色散和衍射色散的影响,如图12中的两曲线交叉点,其横坐标值约为0.35 mm,即柱面透镜宽度为0.35 mm时,接收屏上白光光斑可完全消色差.

图11 实验得到的RGB三基色光强度分布曲线Fig.11.Experiment colored light intensity distribution curves of RGB.
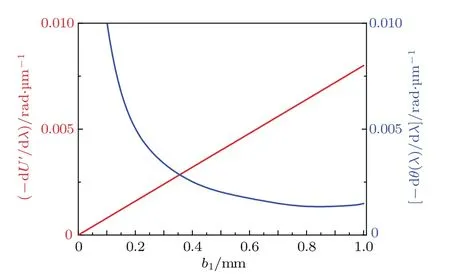
图12 折射色散和衍射色散与柱面透镜出射光束宽度的关系Fig.12.Relationship between the dispersion and diffraction dispersion with the width of the beam.
4.3 色散对轴外平顶光束的影响
当蝶形小孔偏离柱面透镜光轴较大时,光束在光轴的上方或下方,折射色散为非对称结构,不能抵消对称结构的衍射色散,其结果是波长较短的蓝光和波长较长的红光形成的平顶光束存在相对位移,不同波长平顶光束存在的相对位移使白光光束展宽、边沿颜色分离和平顶因子变小,如图13(b)所示(其中蝶形小孔偏离光轴距离R,R为柱面透镜半径).与图13(a)所示的轴上衍射图相比,在图13(b)中可以看到明显的彩色条带和三基色光强分布曲线错位,光束平顶特性变差.
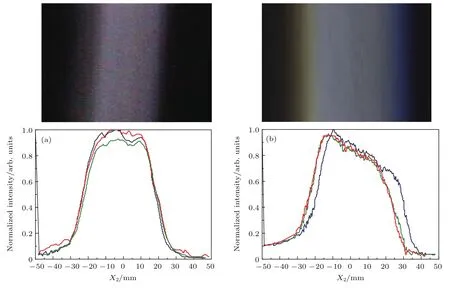
图13 柱透镜轴上的衍射光强分布(a)和轴外的衍射光强分布(b)Fig.13.Diffraction intensity distribution at optical axis of a cylindrical lens(a),and at offaxis of a cylindrical lens(b).
4.4 其他因素对轴外平顶光束的影响
1)像差的影响
从图13(b)还可以看到,蝶形小孔在柱面透镜轴外位置产生的衍射光束横向光强分布顶部出现明显的倾斜,这是由柱面透镜的像差引起的衍射像中的光强分布不均匀现象.柱面透镜的像差主要考虑初级球差、初级慧差和初级像散的影响,而初级慧差是轴外物点宽光束经光学系统后产生失对称像的主要因素.
2)蝶形小孔尺寸的影响
当蝶形小孔尺寸远小于柱面透镜曲率半径时,蝶形小孔类似点光源,其经过柱面透镜后的衍射光束横向光强分布接近高斯分布,而不具备平顶特性.当蝶形小孔尺寸接近柱面透镜曲率半径时,由于像差的影响将使平顶特性变差(如图13(b)).可见蝶形小孔尺寸应选择比柱面透镜曲率半径小1—2个数量级之间为宜.
5 结 论
由广义惠更斯-菲涅耳衍射积分和多波长叠加原理推导出白光LED背光源均匀光场经过蝶形小孔阵列衍射掩模片和柱面透镜后的光强分布并进行了数值模拟和实验验证.实验用蝶形小孔阵列衍射掩模片产生了白光横向平顶光束,实验得到的横向光强分布、横向平顶光强分布与距离的关系和平顶因子计算结果均与数值模拟结果相符.结果表明:当蝶形小孔的宽度h=48µm,凹度β=0.50—0.66,柱面透镜曲率半径R=2.67 mm,厚度d0=8 mm时,在可视距离500—2000 mm范围内得到平顶因子F>0.89的横向白光平顶光束,且平顶光束的横向宽度随着传播距离的增大而增大.对白光横向平顶光束消色差进行了讨论,证明了折射色散和衍射色散可以互相抵消,实现无色差白光横向平顶光束.研究结果对于定向背光式自由立体显示器中的应用有重要参考价值和指导意义.

