基于Pearson相关系数的货运车辆能耗模型研究

蔡 静，张明辉，朱宇婷，刘宇环

(1.北京工业大学，北京100124；2.北京交通发展研究院，北京100073)

0 引言

“十二五”期间，交通行业处于大规模运输与建设阶段，交通运输能源消费总量与强度是决定未来能源安全与温室气体排放控制成败的关键要素.因此，在“十三五”时期国家要求对能源消费总量、能源消费强度及碳排放强度进行约束控制的背景下[1]，控制货运行业燃油消耗已成为节能减排工作的一个重要突破口.为了配合货运行业的工作顺利开展，需要对行业的燃油消耗进行分析与预测，以辅助制定车辆发展思路.

国际上已有一些国家的相关部门对机动车能耗进行了调查与研究，但大多都聚焦于机动车的单车燃耗与节能，Tseng等[2]介绍并比较了单车能耗预测方法，包括识别驾驶员/车辆/环境相关因素的黑匣子框架，以及基于矩阵分解的协作过滤方法；Guensler等[3]通过分析高性能车辆排放建模系统，即机动车排放模拟器，得出基于车辆运行模拟单车二次燃料消耗与排放的方法；Lorf等[4]通过分析皇家汽车俱乐部的2011年RAC未来汽车挑战赛的结果发现，该车型的动力传动系统对能耗与排放影响最大，牵引比率及再生制动量对单车能耗有显着影响，平均车速对25～70 km/h范围内的车辆能耗没有太大的影响；Jovicic等[5]通过优化公共交通工具路线来估计减少燃料消耗的潜力，预计可减少20%的成本与相关排放量.

国内则大多聚焦于货物运输宏观能耗影响研究，刘艳楠[6]通过基于能源消耗的货物运输结构优化模型，提出影响货物运输能源消耗的因素主要有社会经济发展水平、货物运输能源强度、货物运输结构及货物运输服务量；张雪青等[7]运用完全分解模型对浙江省货物运输分别进行了关键能耗影响因素分析，包括运输周转量、运输结构与能耗强度等三因素；马超云等[8]对我国铁路能耗影响因素开展了分析；高有景[9]认为公路条件、车辆特性、交通流条件、驾驶员的操作水平、交通管制等都会对公路运输能耗产生重要影响；刘广海[10]系统地建立了冷藏运输能耗分析模型，对货物品类、运输季节等众多因素对能耗的影响逐一进行了分析，但这些研究无法反映车型变化和车辆结构调整对能耗的影响.在车型众多、结构调整政策频出的情况下，难以评估和预测对于能耗的影响.

目前针对不同货运车型燃料消耗分析，主要依托实测法和非线性回归分析开展研究.Odhams等[11]利用实际测试研究影响某种重型货车能耗的关键因素，包括车辆配置(车辆数量)、交通拥堵、速度等，但无法抽象建立涵盖不同车型的核算分析.陈建华等[12]通过应用面板门限回归模型，分析平均运距、里程利用率、工作率与吨位利用率等因素对车辆单耗的影响，但对于平均运距等因素引起显著门限效应和部分分段区间变量点机理无法做出合理解释.

本文在对货运车辆运行调查数据处理的基础上，利用Pearson回归方法对能耗和各影响因素两者间正态连续变量开展等变量间的线性相关性分析，根据客观机理和特点，解决了车辆能耗分段突变点和相关性合理解释，实现了对车辆百公里能耗的关键影响因素进行判断，建立了基于单车的车队能耗核算模型.

1 基础数据

本文主要利用2013—2015年年度规模相近、总计约24 000份的不同车型货运车辆百公里能耗等运行调查数据，对单车能耗影响因素进行了回归分析.根据北京市货运车辆结构特点和政策性管理及调控要求，车型结构主要考察罐车、牵引车、挂车、栏板货车、厢式货车和自卸车共6类；燃油类型涵盖柴油、汽油与天然气；标记吨位主要分析载重量在3.5 t以下到8 t以上的货车；车龄主要考察15年以内的货车，按照上述关键要素对北京市营运货车开展分层等比例抽样.所有数据样本调查均在4月和9月2个时段内获得，避免因在冬季、夏季开空调引起的数据偏差.通过各层调查样本中，部分安装的车载油耗仪或定位系统结合累计油耗，对平均百公里油耗进行校验，调查数据与监测数据相差10%以上需更换该层调查样本.得到有效样本数据如表1所示.

表1 共有统计量基本情况Table 1 Basic statistics of common statistics

2 研究方法

关键影响因素分析一般包括统计与计量两种递进的分析方法，在统计分析中，研究变量间相互关系常用的分析方法包括画散点图、计算Pearson相关系数、进行简单的双变量单因素方差分析或进行非参数分析[13].

由于现有关于Pearson相关系数适用于两个正态分布的连续变量开展等变量间的线性相关性分析，广泛应用于度量生物物种的亲缘关系[14]、股票间相关性[15]、期刊引用关系[16]等方面，本文将采用Pearson相关系数度量货运车辆能耗与影响因素之间的相互关系.

Pearson相关系数用来度量两个变量X与Y之间的相互关系，被广泛应用度量两个变量线性相关的强弱，总体相关系数用ρ表示，样本相关系数用r表示.

(1)计算公式.

总体相关系数为

式中：μX=E(X)；μY=E(Y)；σX表示总体标准差.式(1)对于样本的Pearson相关系数同样可用.

样本相关系数为

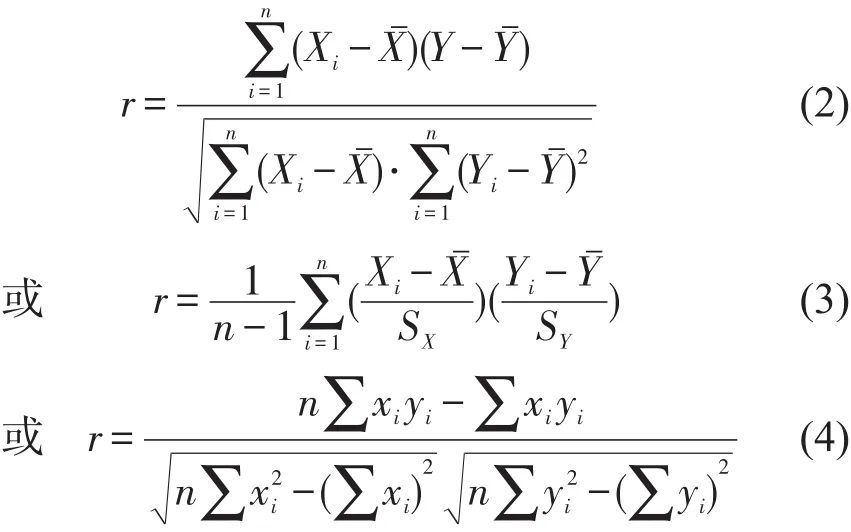
(2)相关系数的假设检验.

首先，提出假设.

H0：ρ=0无关

H1：ρ≠0相关

其次，确定显著性水平：α=0.05.

如果从相关系数ρ=0的总体中取得某r值的概率P>0.05时接受假设，此r值很可能是从总体中取得，两变量间无显著关系；如果取得r值的概率P≤0.05或P≤0.01时，在α=0.05或α=0.01水准上拒绝检验假设，认为该r值不是来自ρ=0的总体，而是来自ρ≠0的另一个总体，因此判断两变量间有显著关系.

最后，计算检验统计量，查表得到P值，如果拒绝H0，则两变量相关；否则，两变量无关.

其中，由于来自总体的所有样本相关系数呈对称分布，所以通过t检验法计算检验统计量tr，查t界值表，得到P值，tr的计算公式为

计量分析是研究变量在数据上的因果关系，通过实际经验与回归结果，判定变量间的因果关系，以及不同变量对目标变量的边际影响效应的大小.计量分析方法的本质是通过回归方程的设置来构建1个模拟的控制实验环境，在此环境中研究兴趣变量之间的关系.本文将采用计量分析方法来分析车辆特征数据与百公里油耗数据之间的因果关系[14].

3 货运车辆单车能耗

3.1 单车百公里油耗模型

由于模型中加入交叉项会导致其他解释变量的系数不显著，在权衡模型拟合度与模型简便性后，选择考虑全部样本的共同变量且便于计算的模型作为最优方案，即

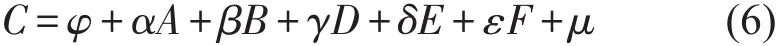
式中：C表示百公里油耗；φ表示回归方程的常数项；A表示车龄的高次项；B表示标记吨位的高次项；D表示行驶里程的高次项；E为考察燃油类型的虚拟变量，主要区分柴油货车与汽油货车的燃油消耗差异；F为考察货车结构的虚拟变量，用以区分不同车辆类型的差异；μ则表示回归结果的方差.

为初步明确百公里能耗的可能影响因素，判断因素间的关系，本文对吨位、车龄与车型结构3个因素，分别采用Pearson相关系数方法与计量分析方法进行分析，具体分析如下.

(1)吨 位.

将标记吨位划分为：载重量3.5 t以下的为轻型载货汽车，4～8 t的为中型载货汽车，8 t以上的为重型载货汽车.对其进行分析，结果显示，吨位对于单车百公里油耗有显著性影响，具体结果如表2所示.

表2 吨位的计量回归结果Table 2 Tonnage of the metrological regression results

(2)车 龄.

将车龄分为(0,3]、(3,6]、(6,10]与(10,15]共4个区间范围.对其进行分析，结果显示，车龄对于单车百公里油耗有显著性影响，具体结果如表3所示.

表3 车龄的计量回归结果Table 3 Vehicle age of the metrological regression results

(3)车型结构.

对6类车型结构进行分析，结果显示，车型结构显著影响百公里油耗，且边际效果很大，具体结果如表4所示.

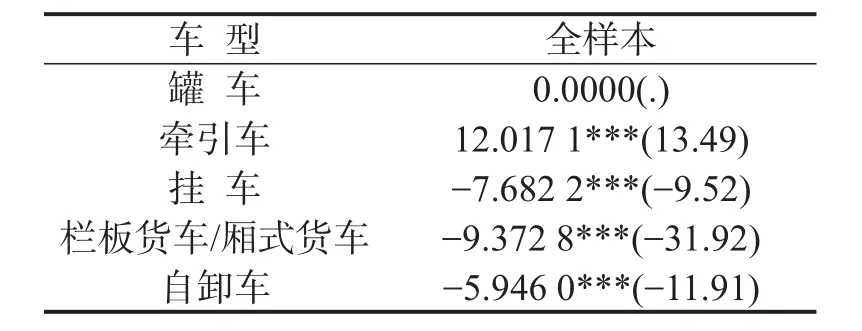
表4 车型结构的计量回归结果Table 4 Vehicle structure of the metrological regression results

(4)对所有样本分析的常数项拟合度进行分析，最优结果如表5所示.

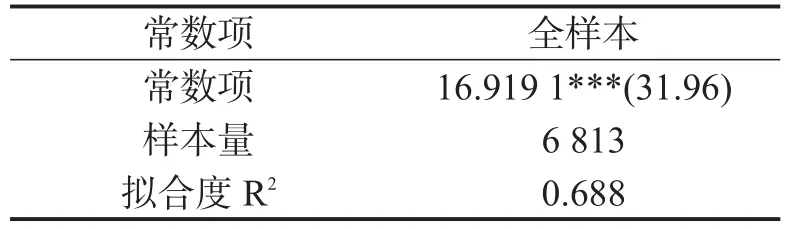
表5 常数项与拟合度结果Table 5 Constant term and fitting degree results

根据上述对吨位、车龄与车型结构变量的分析，结果显示吨位的三次项变量在回归模型中边际影响效果很小，车龄的二次与三次项都没有显著影响，所以舍弃以上变量.因此在最终预测模型中，只选择车龄一次项、吨位一次项、吨位二次项与车型结构作为解释变量，重新对全样本数据回归得到系数.

式中：A代表车龄一次项，B1表示标记吨位一次项；B2表示标记吨位二次项；ε代表车型结构，ε取值如表6所示.

表6 ε取值Table 6 Value ofε

对模型预测结果进行检验，结果发现由回归模型推出的预测模型对车辆的百公里油耗的拟合结果约有95%的准确度，拟合度为0.675 6，实现了北京车辆结构特点下多维要素单车百公里能耗量化输出，具体如图1所示.

图1 百公里油耗真实值与拟合值的对应分布图Fig.1 Corresponding distribution diagram of the true value and fitting value of per hundred kilometers oil consumption

除车辆技术指标外，实际能耗另一重要因素为人为操作性影响，该因素并未纳入本研究范围.已有研究表明其影响程度一般在10%以内[17].但随着车辆绝对能耗的增加，实际能耗数据分布范围会逐步扩大.因此该模型拟合度预计将呈现随绝对能耗增加逐渐趋于离散趋势.实际拟合结果也基本符合这一趋势，该预测模型对百公里油耗低于20 L/(100·km)的数值拟合结果很好，大于20 L/(100·km)的数值拟合结果一般，离散程度略大.

3.2 车队能耗模型

基于以上分析确定单车的年度燃油消耗量模型，对辅助考察将来相关工作具有一定的指导意义，具体模型为

式中：Ct表示单车的年度燃油消耗量；G表示单车的年均行驶里程.

4 案例分析

近年来以环保为目标的车辆结构更新进度不断加快，货车作为主要污染源，淘汰老旧车辆是一项核心工作，同时对货车的限行措施和范围也逐步扩大.北京市货车平均车龄由2014年的8.3年降至2016年的7.2年，货车总量由2014年的30.8万辆上升至2016年的35.1万辆，年均行驶里程不同车型呈现差异化变化，但年均行驶里程增速逐步降低.

利用本研究建立的模型，结合车辆定位监测数据，对2016年相比2014年的能耗变化情况开展了分析.模型拟合结果显示，尽管车辆总量增长明显，但由于车辆结构优化调整和限行措施影响，柴油消耗量均呈现下降趋势.

车龄优化、吨位变化、车型变化、分车型车辆数和行驶强度变化带入全市车队能耗模型，基于各因素对能耗贡献率影响分析情况如图7所示.

表7 柴油能耗变化情况Table 7 Change of energy consumption of diesel oil

对比统计局公布能耗数据，柴油总量核算偏差均小于5%，模型核算准确度较高，如表8所示.

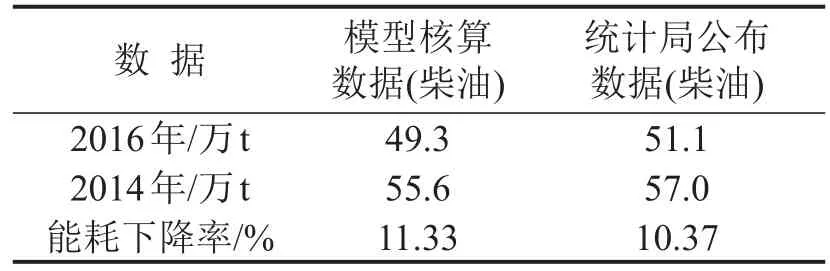
表8 能耗下降率Table 8 Drop rate of the energy consumption

5 结 论

将Pearson相关系数创新地应用到货运车辆能耗问题中，把影响货运车辆能耗的各种因素进行精细量化，得到货运车辆能耗的关键影响因素有吨位、车龄与车型结构，构建基于Pearson相关系数的单车能耗模型来测算货运车辆能耗，以精确核算年度货运行业能耗总量与行业季度能耗总量为目标，研究不同情景下的行业能耗核算方案，得出相应的核算方法，为货运行业节能减排工作开展效果的精准核算和考核提供了技术与理论支撑，具有重要的实际应用价值.通过北京市货运政策对模型各种参数影响的案例分析，验证模型能有效减少货运燃油消耗，实现节能减排的效果.