城市快速路车速离散特征及其影响因素研究
刘莹莹,李 健,陈小鸿
(1.同济大学建筑设计研究院(集团)有限公司交通规划设计院,上海200092;2.同济大学交通运输工程学院&道路与交通工程教育部重点实验室,上海201804)
0 引言
城市快速路系统是大城市交通主骨架,随着我国城镇化和机动化的迅猛发展,城市快速路已不堪重负.在北京、上海等超大城市,城市快速路在高峰时段车辆走走停停,车速离散现象明显,具体表现为个体车辆行驶车速不稳定,加减速频繁,使交通流偏离原本稳定、均衡状态,导致道路事故率上升、通行能力下降、环境污染等一系列问题,从而进一步加剧车速离散性,使整个快速路系统陷入恶性循环,严重影响其运行效率和安全.
交通流基本图模型是针对宏观交通运行特性指标间关系进行分析与建模的理论与方法,是交通流理论和交通工程学科的基石.传统方法致力于对连续流特征参数(流量、密度、速度)间基本关系的研究[1].研究多以交通流车辆不受外界因素干扰、以均一稳定车速行驶为假设前提,以车辆行驶的平均状态指标为研究对象,建立理论模型以最佳描述连续流流密速基本关系.近年来,随着自动检测设施的大规模安装,基于实证数据的交通流运行特征经验分析取得了重要进展.交通流基本图的研究逐渐从传统平均特征指标为主的确定基本图转变为平均和离散特征指标并重的随机基本图[2].
近年来,许多学者试图将车速离散特征与传统交通流基本图关联起来,将反映平均交通流参数特征的传统基本图拓展为反映交通流参数均值和方差特征的随机基本图.Wang等[3]利用中国南京的高速公路数据分析了车速方差,证实交通密度可表示为速度变异系数的指数函数,从而将车速离散特征与传统交通基本图联系起来.Wang等[4]采用速度标准差作为描述车速离散特征的方式,利用随机建模方法建立了速度标准差与交通密度和平均速度之间的关系.Chung等[5]比较了车速离散特征不同的描述方式,认为速度变异系数可表达为密度的指数函数和平均速度的负指数函数,而速度标准差则不能与传统交通流参数建立模型关系.然而上述研究对象多是高速公路,研究数据多采用线圈采集的集计数据,缺少基于个体单车车速的城市快速路车速方差特征研究.
本文采用上海车牌识别系统采集的个体车速数据,基于随机基本图对城市快速路的车速离散特征及其影响因素进行研究.车速离散指标选择个体与集计车速方差(SDS),并比较两者的差异性.与线圈检测器采集的集计车速数据不同,此处采用个体车速数据,车速方差(SDS)可直接计算得出.此外,本文研究对象为市区城市快速路,与高速公路相比,城市快速路受上下匝道影响显著,交通流特性介于连续流和间断流之间,可与以往研究结果比较验证.
1 数 据
本文选取上海市延安高架快速路主线断面为研究对象.延安高架是上海市1条东西走向的主通道,西起虹桥机场,东至外滩,全长约15 km,具有常发性拥堵特征.其车牌识别器主要布设在主线及入口匝道,布设方位如图1所示.
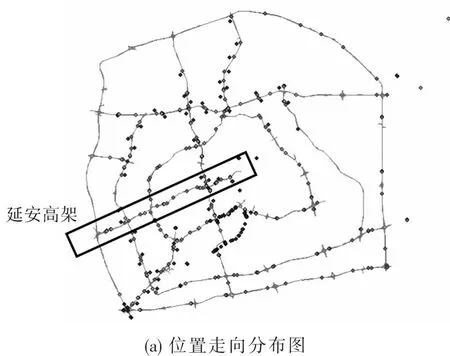

图1 上海延安高架位置走向和车牌识别断面分布图Fig.1 The location and detailed positions of main line sections on Yan’an Elevated Expressway in Shanghai
1.1 交通数据
交通数据采集自上海车牌识别系统.系统覆盖了上海市高架道路主线和部分匝道,包含过江桥隧及部分地面道路,共349个检测断面,包含268个快速路和81个地面道路检测断面(图1中散点).原始数据(15GB txt.)采集自2012年,总量2.8×108条,共含7个字段,数据格式如表1所示.本文重点研究上海延安高架13个主线断面同年10月的车速数据,有效样本总量2.5×107条.

表1 原始数据格式Table 1 Data format
1.2 数据清洗
数据清洗剔除由检测器异常引起的“0”值和异常值数据.全月每日识别非零率在95.8%~96.9%之间,平均识别非零率为96.2%.此外,延安高架同时段共得236条事故,据“常态分析原则”,同时考虑样本事故影响时间,将事故发生1 h内的交通数据全部剔除.
1.3 数据算法
(1)个体车速空间标准差.
原始数据为点车速,需转化为空间车速以模拟变量间关系.统计时间间隔为5 min,计算公式为

式中:i为对应于第i个5 min间隔的i分组,其中1≤i≤Ni;m为i分组中的m观测值;Ni为i分组的速度观测值总量;为i分组的时间平均车速;vm(ti)为i分组中m观测值对应的车速;为i分组空间平均车速;为i分组时间平均车速方差;为i分组空间平均车速方差;σi(si)为i分组空间平均车速标准差.
(2)集计车速空间标准差.
以集计空间车速标准差(σki(si))代表前人研究中针对不同交通流密度处理车速离散的方法,并与个体车速空间标准差(σi(si))比较.将集计车速数据划分为m组,对应密度k处的每一个i分组,指标计算公式为

式中:ki为交通流密度k处的i分组;m′为ki分组中的m′观测值,其中1≤m′≤Ni;Ni为ki分组中集计车速观测值总量;为ki分组样本时间平均车速的均值;为ki分组中m′观测值的时间平均车速;为ki分组样本空间平均车速的均值;为ki分组集计车速的时间平均车速方差;为ki分组集计车速的空间平均车速方差;σki(si)为ki分组集计车速的空间平均车速标准差.
2 随机基本图特征与分类
2.1 个体与集计车速方差比较
传统交通流研究领域,流密速关系往往以“成对”指标间确定性模型表征.现实状况下,交通流特定水平下的密度所对应的车速并非一个定值而是一个分布,这也恰与车速随机属性吻合.前人研究多以检测线圈采集得到的集计车速数据,发现车速方差曲线为一个开口向下的抛物线形态,峰值(较大波动)在对应路段通行能力范围取得.Wang[4]利用美国高速公路实测车速数据取得的研究结果可为此类代表,如图2所示.

图2 美国高速公路(Gerogia 400)不同时间间隔集计数据(星期一)Fig.2 Data curves with different intervals of time aggregation on Monday from Georgia 400,USA
由个体车速直接计算的车速方差与上显著不同.图3展示了延安高架主线M04断面的车速方差.个体车速标准差(SDS)整体稳定于5~15 km/h范围,随密度增大而小幅下降.将纵轴范围缩减至0~30 km/h(图3(a)),比较集计(方块)与个体(星号)方差差异.发现集计标准差整体数值较小(2~5 km/h),呈两端低中部高的近抛物线型;个体车速标准差(5~15 km/h)则呈两端集中中部散布的随机形态.图中曲线显示个体车速标准差均值大体为同密度集计车速标准差的2倍.
2.2 延安高架实测随机基本图分类
延安高架各主线断面随机基本图如图4所示,其中,Q为交通流量(veh/lane/day),NL为车道数,DNR为最近匝道距离(m).
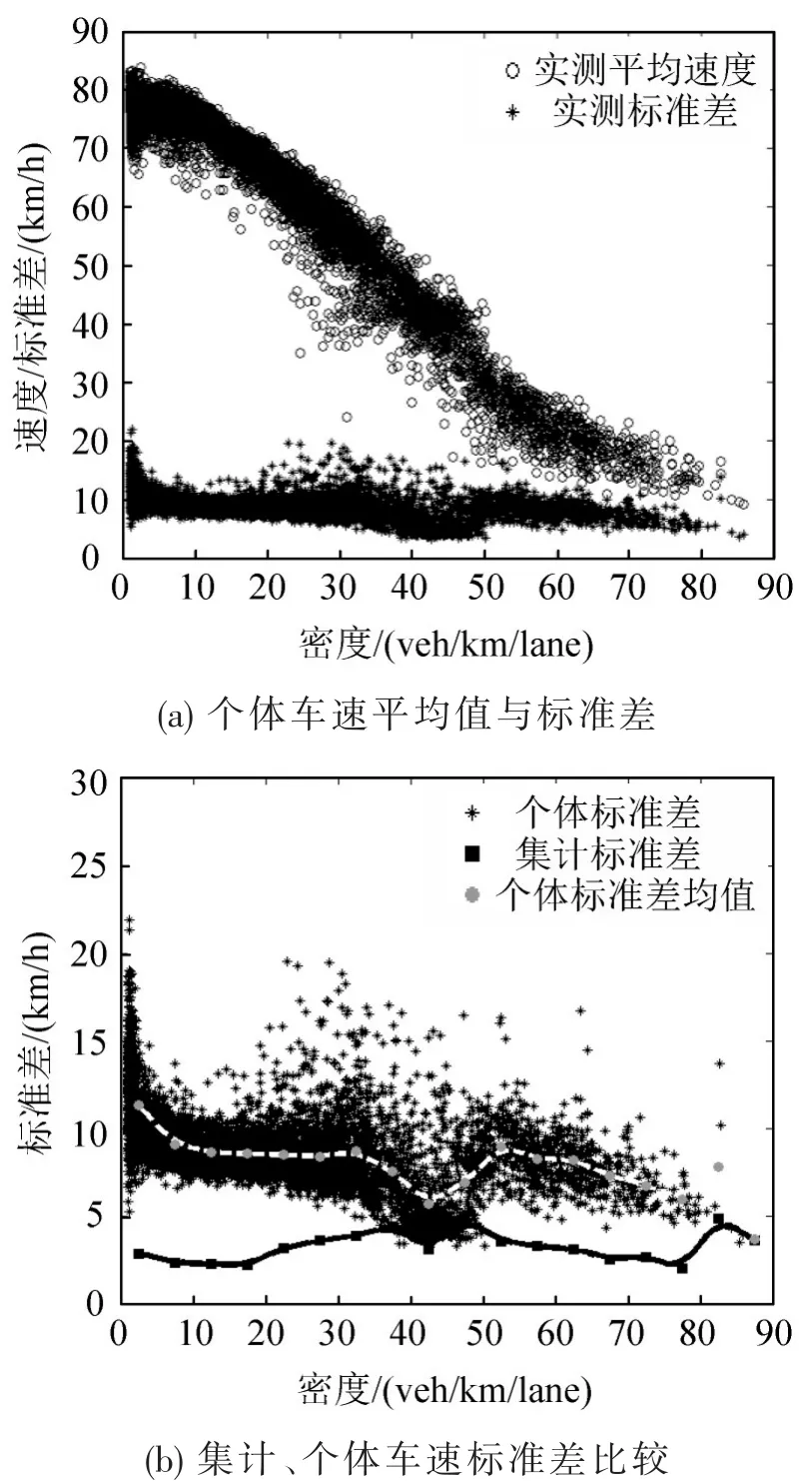
图3 2012年10月M04断面个体、集计车速标准差Fig.3 Individual and aggregated SDS of M04 in October,2012
根据上述个体车速方差散点分布的范围、形状和趋势,将其划分为以下4类:
(1)稳定型(M04).
不同密度车速方差基本稳定,包括M04、M06、M07、M08和M14.流量水平整体较高,约20 000 veh/lane/day,推测流量是主要影响因素.
(2)递减型(M09).
车速方差散点在密度范围整体或前半部呈递减趋势,包括M01、M05、M09、M10、M11和M12.所选因素影响效果未知,推测图像形态由交通信号、断面渠化等其他因素或各因素间交互作用导致.
(3)抛物线型(M13).
方差散点呈明显抛物线型,峰值于路段通行能力处取得(40 veh/km/lane).M13断面是紧邻延安路隧道出口的下游断面,自由流车速60 km/h,单向2车道,且上游261 m隧道内无其他出入口.


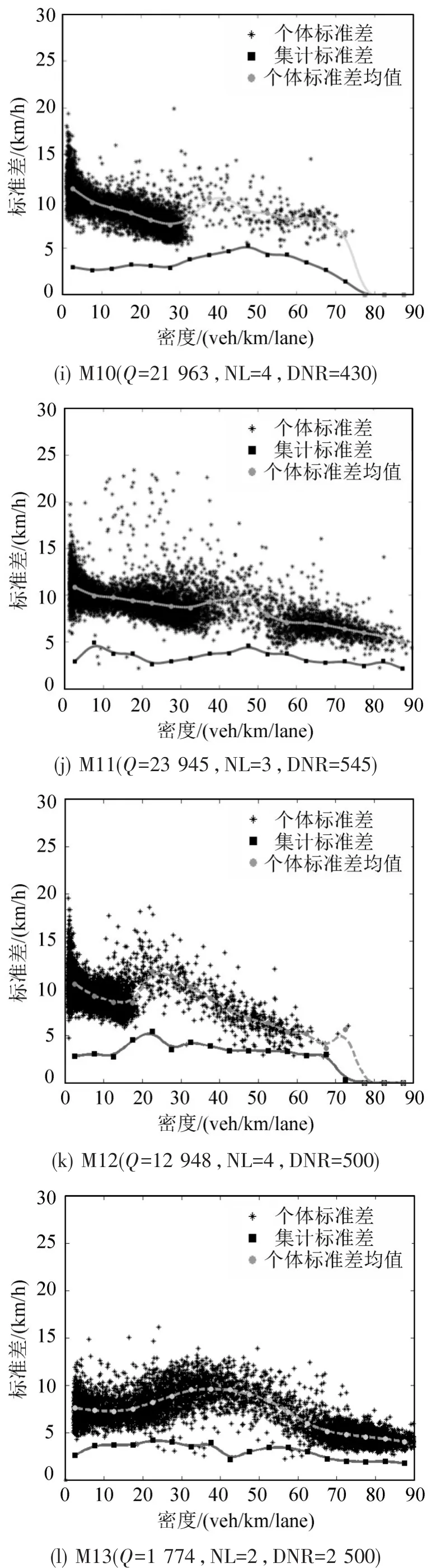
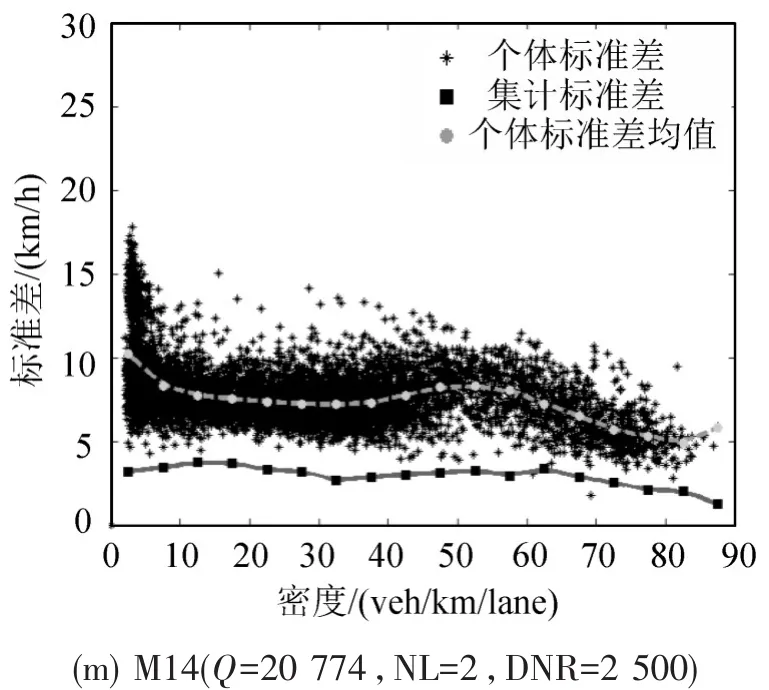
图4 延安高架主线断面实测SDS分布Fig.4 Empirical SDS diagrams of main line sections on Yan’an Elevated Expressways
(4)集群型(M02).
方差散点在低于10 veh/km/lane密度范围内集群分布.M02断面远离市区中心,接近外环高架路,日均车流量仅3 944 veh/lane,远低于其他断面平均流量水平.推测流量和地理方位是主要影响因素.
3 基于多源线性回归的车速离散影响因素辨识
本节旨在通过多元线性回归进一步辨识车速离散的影响因素,并量化其影响程度.
3.1 车速分布特征解释变量
现有文献[6-7]表明车速分布受多种因素影响,主要包括车速均值、85百分位车速、车速标准偏差、方差系数、“超限车”比例、“超限车”平均超速值等.其中与限速相关的2个超速参数定义如下:
①“超限车”比例,超过限速要求的车速比例(%),以Pex表示;
②“超限车”平均超速值,“超限车”平均车速—路段限速(km/h),以Vex表示.
Vex表征了车速分布中“上尾巴”的形状,对于给定的Pex值(数值大小取决于“上尾巴”面积),一般而言“上尾巴”越长则Vex数值越大.图5描绘了车速分布典型特征.
3.2 多元线性回归
将车速离散数据与相应路段其他特征指标对应建立多元线性回归模型.车速离散/波动性不仅与车流中高速车相关,理论上也应受低速车的影响.延安高架为城市快速路,只规定最高限速,尚未规定最低限速.本文根据车速分布“对称性”原则,以“15百分位车速”确定各断面最低限速.汇总各断面限速标准如表2所示,主线路段与匝道的7种组合类型如图6所示.

图5 典型车速分布Fig.5 Typical speed distribution
回归变量包括路段车速分布特征变量、交通流特征变量及路段几何特征变量.除“85%SDS”为因变量外其余变量均为自变量,变量描述如表3所示.
应用SAS 9.2软件对样本数据建立多元线性回归模型.以延安高架13个主线断面每日数据为1条样本记录,2012年10月30天共得390条样本记录.每条样本记录包含1项Y变量“SDS”和其余10项X变量,设定显著性水平0.15,逐步回归9步变量筛选,最终标定结果如表4所示,回归诊断及残差图如图7和图8所示.
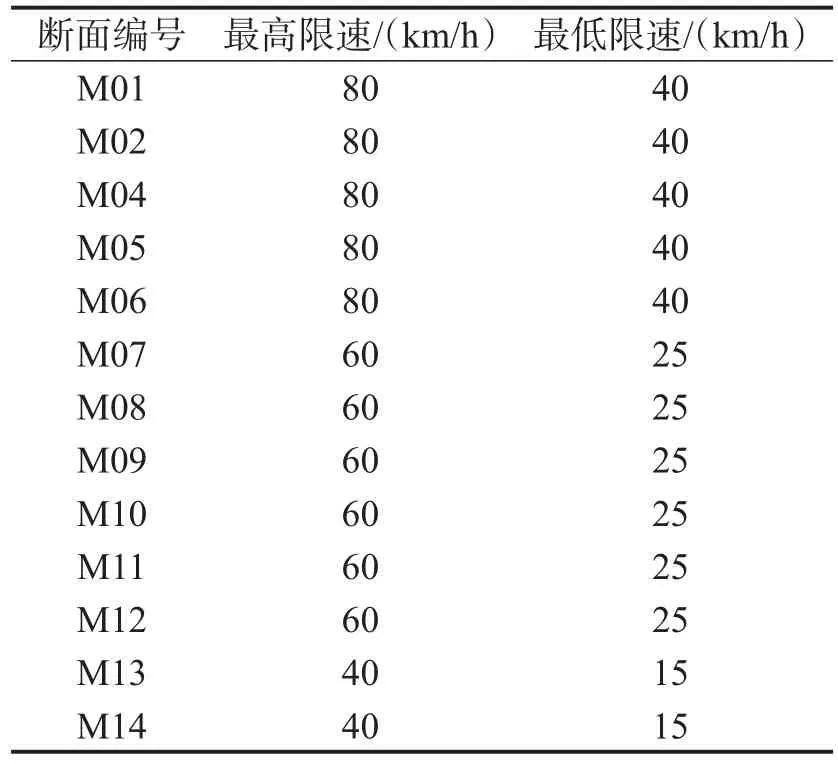
表2 延安高架主线断面限速Table 2 Speed limits of main line sections on Yan’an Elevated Expressways
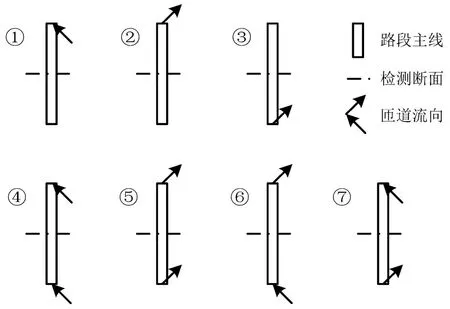
图6 路段—匝道组合类型Fig.6 Road section-ramp composed types
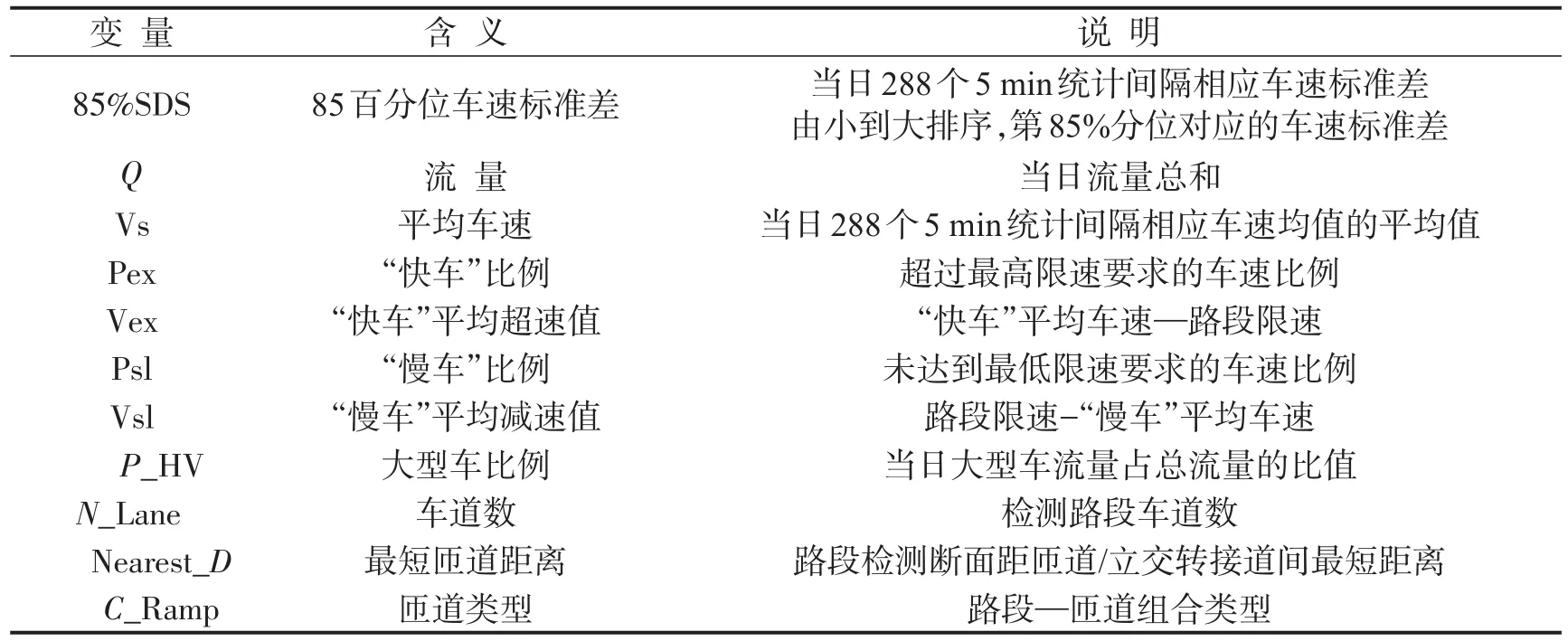
表3 回归模型变量Table 3 Regression model variables

表4 回归参数标定结果Table 4 Calibration results of regression parameters

图7 方程拟合诊断Fig.7 Fit diagnostics for SDS

图8 自变量残差图Fig.8 Residual by regressors forSDS
最终回归方程式为

由回归方程,除变量“大型车比例P_HV”,其余变量均满足0.15显著性水平.延安高架主线车流大型车无货运车,仅有大客车占比约1%,对整体车流波动影响微弱,故不显著.因变量“85百分位车速标准差”与“平均车速Vs”正相关,与“流量Q”“最短匝道距离Distance”负相关.车速极端值对离散的影响效应相反,“慢车比例P_Sl”为正,“快车比例P_Ex”为负,系数绝对值相近;“快车平均超速值Vs_Ex”与“慢车平均减速值Vs_Sl”拟合系数相比,前者约为后者的7.4倍,表明同等条件下,快车比慢车对离散影响更为灵敏,佐证了现有限速标准首要“限制高速”的必要性.方程同时表明分类变量“车道数LaneNo”和“匝道类型Ramp”对车速离散影响显著,即优化道路渠化设计对提高车流稳定性、安全性有重要价值.
4 结 论
本文使用上海车牌识别系统采集得到2012年10月的车速数据,以延安高架13个主线断面为研究重点,分析了实测个体车速的离散特征规律与影响因素,主要结论如下:
(1)随机基本图个体车速标准差整体稳定(5~15 km/h),随密度增大而小幅下降,呈两端集中,中间散布的随机形态,其均值大体为同密度条件下集计车速标准差的2倍.
(2)依据实测随机基本图散点分布特征,将其划分为稳定型、递减型、抛物线型和集群型4类,并推测断面日均流量和地理方位是主要影响因素.
(3)将路段车速离散指标与其他指标对应建立多元线性回归模型.因变量“85百分位车速标准差”与“平均车速Vs”正相关,与“流量Q”“最短匝道距离Distance”负相关.车速极端值对离散的影响效应相反,快车比慢车更为显著灵敏.分类变量“车道数LaneNo”和“匝道类型Ramp”也对车速离散影响显著.
本文采用的高精度个体车速数据使车速离散指标得以直接计算,建立多元线性回归模型,特别选取了Pex、Vex、Psl和Vsl变量表征“极端值”对整体车速分布的影响,为识别车速离散特征影响因素提供了新的思路与方法.研究成果对类似城市/地区采取相关交通管控措施可提供一定参考与借鉴.然而,研究基于特定时期延安高架个别断面数据,且数据清洗尚不完美,结论的客观普适性有待进一步检验.

