基于IPSO的风光高渗透电网抽水蓄能电站容量优化∗

彭 毅，李凤婷，辛超山，陈伟伟

(1.新疆大学电气工程学院，新疆乌鲁木齐830047；2.国网新疆电力有限公司经济技术研究院，新疆乌鲁木齐830011)

0 引言

由于风电与光伏发电出力具有较强的随机性与波动性[1,2]，且我国新能源发电高比例接入区域电网结构薄弱、调峰能力不足，现阶段我国面临严重的弃风弃光问题.因此，提升大规模风电与光伏发电的并网容量已成为亟待解决的难题[3].

针对上述问题，为优化抽水蓄能电站的容量，国内外专家与学者开展了大量研究，通过对抽水蓄能电站的建模分析[4−6]，基于对不同影响因素的考虑，其优化目标主要可分为以下几类：(1)考虑风电抽水蓄能电站联合系统的利益最大化，以电量效益最大为目标[7−9]；(2)考虑风电出力波动影响，同时考虑电量效益和总体出力平稳的多目标优化[10−12]；(3)在考虑上述优化目标的基础上，加入风电与光伏发电的潜在环境效益的多目标优化[13].上述文献虽然就抽水蓄能电站容量优化问题开展了大量研究，但所获得的研究成果往往忽略抽水蓄能电站的电能时空转移效益以及增强系统调峰能力的效益.

本文基于对抽水蓄能电站充放电数学模型的构建，提出一种考虑电量效益、电能时空转移效益、环境效益、调峰效益以及初始投建成本、运维成本与废弃电站处理成本的抽水蓄能电站容量优化方法，并采用IPSO算法对电站容量优化配置模型进行求解.参考新疆某含大规模风电与光伏发电的区域电网的运行数据，基于MATLAB平台，对本文所提出方法进行仿真验证.

1 基于新能源发电并网消纳提升的抽水蓄能电站充放电模型构建

1.1 抽水蓄能电站充电状态模型构建

谷荷区电网旋转备用不足是使新能源发电高渗透率区域电网弃风弃光问题的主要原因[14].因此，实现新能源发电出力的能量时空合理转移将成为降低新能源发电对旋转备用容量需求以及提升其大规模并网的关键.全网负荷低谷时段弃风弃光总体功率计算模型如下

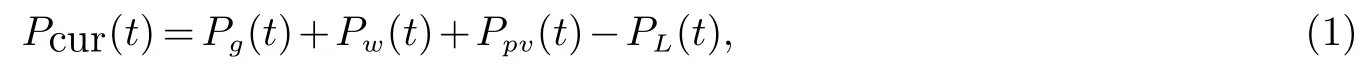
式(1)中，Pcur(t)为t时刻弃风弃光总体功率；Pg(t)、Pw(t)、Ppv(t)分别为t时刻常规发电机组、风电场与光伏电站的总出力；PL(t)为t时刻区域电网总负荷出力.其中，Pg(t)需满足常规发电机组边界极限运行参数约束，如式(2)所示

上式中，n为负荷低谷时段并网常规发电机组总数目；Pg,m(t)与Pg,m,min分别为t时刻第m个常规发电机组的出力值与第m个常规发电机组最小出力限值，由其边界运行参数决定.

针对式(1)，当Pcur(t)>0时，电网旋转备用容量出现不足，电网面临弃风弃光问题(Pcur(t)<0时电网的运行状况相反，此处不做赘述).为此，以降低弃风弃光量为目标，抽水蓄能电站此时应工作于抽水蓄能状态，将弃风弃光电量暂时储存，其需具备的技术特征如式(3)所示

式(3)中，Pps,c(t)为抽水蓄能电站的电能存储功率；Cps,c为抽水蓄能电站的电能存储容量；t1与t2分别为负荷低谷时段的起始时刻与终止时刻.

1.2 抽水蓄能电站放电状态模型构建

与全网负荷低谷时段抽水蓄能电站处于抽水蓄能状态来降低弃风弃光电量的电网运行场景不同，峰荷区内各常规发电机组输出功率往往达到各自的最大值，此时电网的不平衡功率缺额如式(4)

式(4)中，Pgap(t)为全网负荷的高峰时段t时刻的功率缺额，其值大于等于0；其他变量的物理含义同上，区别仅在于表征的是电网负荷低谷时段的各物理量.此时，为保证新能源发电高渗透率电网的稳定运行，抽水蓄能电站需工作于放水发电状态，配合常规发电机组出力满足电网负荷需求，如式(5)所示式(5)中，Pps,dis(t)为抽水蓄能电站的放电功率；Cps,dis为抽水蓄能电站的放电容量；t3与t4分别为负荷高峰时段的起始时刻与终止时刻.

2 抽水蓄能电站容量优化模型构建

2.1 目标函数

抽水蓄能电站容量优化的目标函数主要包括电站初始投资与运维费用以及收益等几个方面，如式(6)所示

式(6)中，f为抽水蓄能电站的总体经济效益；Btotal与Ctotal分别为抽水蓄能电站的收益与投资.其中，抽水蓄能电站的收益如式(7)所示

式(7)中，Bd、By、Be与Bt分别为抽水蓄能电站收益中的电量效益、电能时空转移效益、环境效益与调峰效益，具体计算过程及方法如下.

(1)电量效益Bd

电量效益Bd定义为抽水蓄能电站投运减少弃风弃光电量带来的收益，如式(8)所示

式(8)中，K∗为弃风弃光电量的综合折算价格；λ为弃风弃光电价的折算系数，可由弃风电量与弃光电量的比值确定；Kw为风电的上网电价；η为抽水蓄能电站发电周期转换效率，本文取为0.72.

(2)电能时空转移效益By

电能时空转移效益By为抽水蓄能电站将全网负荷低谷时段的弃风弃光电量转移至全网负荷高峰时段所带来的收益，如式(9)所示

式(9)中，Kp与Kl分别为负荷高峰时段与低谷时段的电能购买价格；ηg与ηp分别为抽水蓄能电站水轮机组运行效率与水泵机组运行效率.

(3)环境效益Be

环境效益Be为抽水蓄能电站通过降低负荷低谷时段弃风弃光电量所带来的常规发电机组污染物排放治理费用的减少量，如式(10)所示

式(10)中，Keg为常规发电机组生产单位电能需付出的环境治理成本.

(4)调峰效益Bt

调峰效益Bt为抽水蓄能电站减小系统调峰压力所带来的收益，如式(11)所示

式(11)中，Kt为抽水蓄能电站为电网提供调峰服务的价格.

此外，抽水蓄能电站的投资Ctotal如式(12)所示

式(12)中，Ct、Cf与Cd分别为抽水蓄能电站投资中的初始投建成本、运维成本及废弃抽水蓄能电站处理成本，具体计算过程及方法如下.

(1)初始投建成本Ct

初始投建成本Ct为折算到全寿命周期的抽水蓄能电站建设与安装成本，如式(13)所示

式(13)中，KE.max与KP.max分别为抽水蓄能电站容量与功率价格；EE.max与PP.max分别为待建抽水蓄能电站的拟定容量与功率；α为年平均成本参数，其计算方法如式(14)所示

式(14)中，x为抽水蓄能电站的设计使用寿命；r为社会折现率.

(2)运维成本Cf

运维成本Cf为抽水蓄能电站日常运行的维护与维修成本，其计算方法如式(15)所示

式(15)中，γE与γq分别为单位容量与单位功率的抽水蓄能电站年运行运维成本系数.

(3)废弃抽水蓄能电站处理成本Cd

废弃抽水蓄能电站处理成本Cd为拟建设的抽水蓄能电站废弃之后的处理成本，如式(16)所示

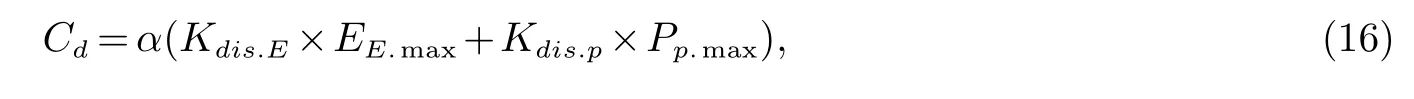
式(16)中，Kdis.E与Kdis.p分别为单位容量与单位功率抽水蓄能电站废弃之后的处理成本.

2.2 约束条件

抽水蓄能电站容量优化的约束条件包括：

(1)满足新能源发电出力的能量时空合理转移需求，可由式(1)～(5)描述；

(2)满足抽水蓄能电站安全稳定运行约束，如式(17)所示

式(17)中，Soc(t)为t时刻抽水蓄能电站的荷电状态；Soc,min与Soc,max分别为抽水蓄能电站允许的最小与最大荷电状态，本文分别取值为0.2与0.8.

3 求解算法

依据上述模型，本文提出的抽水蓄能电站容量优化的目标可归纳为：用尽可能小容量与功率的抽水蓄能电站实现新能源发电出力的能量时空合理转移（由谷荷区转移至峰荷区），降低新能源高渗透率电网调峰压力，提升新能源发电的大规模并网消纳.因此，本文涉及的抽水蓄能电站容量优化实则为一个2变量（拟建电站的容量与功率）、单目标（拟建电站的总体经济性最优）的优化问题.为保证本文构建的抽水蓄能电站容量优化模型求解的精度与速度的双重最优，本文选取的模型求解算法为适用性较强的粒子群优化算法，其物理过程可由式(18)给出

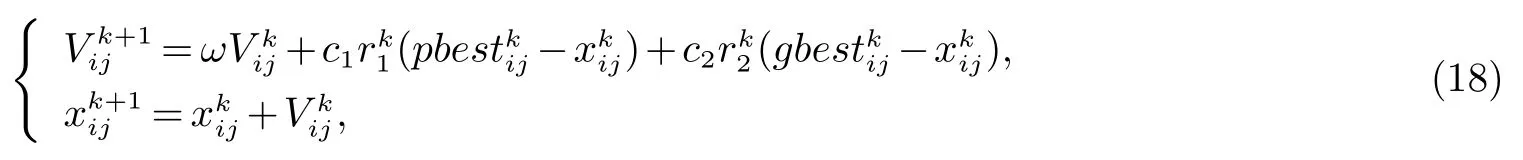
式(18)中，i为粒子次序；j为维度；k为迭代次数；C1与C2为学习因子，本文均取值为2.05；r1与r2均为0～1范围内的随机数；xk+ij1为微粒i经过k+1次运算所在第j维空间位置；Vk+ij1为微粒i经过k+1次运算所在第j维空间速度；pbestk ij与gbestk ij分别为第i个粒子的最优解与群体的全局最优解；ω为惯性权重系数，其决定着模型求解的精度与速度.为此，文章引入非线性动态惯性权重系数提升PSO算法的全局搜索能力，如式(19)所示

式中，ωmax和ωmin分别为ω的最大值和最小值，f为微粒当前的目标函数值，favg和fmin为当前微粒的平均目标值和最小目标值.

具体求解过程如图1所示.

图1 改进粒子群算法流程图

4 仿真验证

4.1 算例条件

文章选取2016年新疆某新能源高渗透率电网实际运行数据仿真验证所提出的抽水蓄能电站容量优化方法.其中，风电与光伏发电的装机容量为1 350MW与800MW，分别占峰值负荷总量的21.9%与12.9%；抽水蓄能电站的充电效率与放电效率分别取值为0.9和0.8，综合效率取值为0.72；抽水蓄能电站的设计使用寿命为20年，内部收益率按8%计算；非常规调峰电量补助Kt为400元/MWh；抽水蓄能电站的功率建设成本与容量建设成本分别取4 260万元/MW与256万元/MW·h；风电与光伏发电上网电价分别取540元/MW·h与800元/MW·h.算法中种群规模大小为30，最大迭代次数为100，惯性权重最大值和最小值分别取ωmax=0.9和ωmax=0.4，常规发电机组电能生产过程中污染物治理费用如表1所示.

表1 常规发电机组电能生产过程中污染物治理费用

参考文献[15]给出的峰谷电价制定指导意见，在结合新疆电网实际运行状况的基础上，本文设定的峰谷电价如表2所示.

表2 本文设定的峰谷电价

4.2 结果与分析

表3为基于上述新疆某新能源高渗透率电网实际运行数据仿真得到的抽水蓄能电站容量优化配置结果.其中，方案1～4仿真计算依据分别为该区域电网2016年4季度(对应为春、夏、秋、冬)典型负荷日的负荷数据与新能源发电出力数据，典型负荷日选取方法参考文献[16]，此处不作赘述.分析可知：（1）相比其他三个季度，依据秋季典型负荷数据仿真得到的抽水蓄能电站容量所获收益最好，全寿命周期综合收益可高达9.94亿元；（2）相比其他三个季度，依据冬季典型负荷数据仿真得到的抽水蓄能电站的配置功率与容量均较大，究其原因为冬季时期部分常规发电机组处于热电联产运行状态，参与电网深度调峰的能力较弱，同时多数地区处于枯水期，水电机组参与系统调峰的能力亦较弱；（3）综合新能源发电出力电能时空合理转移技术指标及新能源发电高渗透率区域电网运行的经济性的要求，本文选取方案3作为抽水蓄能电站容量优化结果.

表3 抽水蓄能电站容量优化配置结果

图2为基于上述区域电网2016年夏季某日实际运行数据仿真得到的抽水蓄能电站实现新能源发电电能时空合理转移的效果.分析可知：（1）经本文优化的抽水蓄能电站参与该区域电网调峰之前，在电网负荷的低谷时段Ⅰ与时段Ⅱ区间，由于常规发电机组最小出力限制，系统面临新能源难以消纳的问题，特别是低谷时段Ⅰ时新能源发电难以并网消纳的容量较大；（2）在抽水蓄能电站参与该区域电网调峰之前，在负荷的高峰时段，受常规发电机组最大出力及新能源发电出力随机降低的限制，系统出现一定程度功率缺额，虽未影响系统的安全稳定运行，但可能致使系统频率出现波动；（3）经本文优化的抽水蓄能电站参与该区域电网调峰之后，在负荷低谷时段Ⅰ与时段Ⅱ区间抽水蓄能电站发挥“抽水蓄能”优势，将“富余”新能源发电出力暂时予以存储，使系统未出现新能源发电难以并网消纳的问题，同时在负荷高峰时段抽水蓄能电站发挥“放水发电”优势，将先前负荷低谷时段Ⅰ与时段Ⅱ区储存的新能源发电“富余”能量予以释放，补偿系统功率缺额，稳定系统频率.

图2 抽水蓄能电站实现新能源发电能量时空合理转移

图3 抽水蓄能电站SOC监测结果

图4 改进粒子群算法优化过程

图3为上述抽水蓄能电站实现新能源发电电能时空合理转移过程中自身运行状态(本文指抽水蓄能电站的SOC)的监测结果.图4为采用改进粒子群算法的求解迭代过程，在迭代25次后趋于收敛，寻得目标函数最优解.分析可知：（1）在负荷低谷时段Ⅰ与时段Ⅱ区间抽水蓄能电站发挥“抽水蓄能”优势，将“富余”新能源发电出力暂时予以存储，使其SOC逐渐增大，而在在负荷高峰时段由于系统功率缺额补偿需要，抽水蓄能电站发挥“放水发电”优势，将先前负荷低谷时段Ⅰ与时段Ⅱ区间储存的新能源发电的“富余”能量予以释放，使其SOC逐渐降低；（2）在抽水蓄能电站参与区域电网调峰能力提升及实现新能源发电电能时空合理转移过程中，其SOC始终处于0.2～0.8预设范围，表明提出的基于IPSO的风光高渗透率电网抽水蓄能电站容量优化思路与方法是正确的、可行的.

5 结论

针对现有的抽水蓄能电站容量优化方法较多忽略其较大的电能时空转移效益与增强系统调峰能力效益，文章提出一种基于IPSO的风光高渗透率电网抽水蓄能电站容量优化方法，得到如下结论：

（1）所建立的抽水蓄能电站容量优化模型不仅关注其全寿命周期内的总体经济效益问题，还同时关注其参与电网调峰能力提升及实现新能源发电电能时空合理转移的需求问题，即所建立的抽水蓄能电站达到经济与技术上的双重最优；

（2）依据2016年新疆某新能源高渗透率电网实际运行数据，该系统需优化配置的抽水蓄能电站功率与容量分别为800MW与3 650MW·h；

（3）经本文优化的抽水蓄能电站在参与该区域电网调峰及实现新能源发电电能时空合理转移过程中，其SOC始终处于0.2～0.8预设范围，即在提升新能源发电并网消纳能力的同时，可保证自身安全稳定运行.