非均匀电势和子晶格势调控下扶手型石墨烯纳米带的电子特性∗

姜莉锋，徐雷，张军

(新疆大学物理科学与技术学院，新疆乌鲁木齐830046)

0 引言

石墨烯自被发现以来[1]，就因为其特殊的蜂窝型晶格结构[2,3]，而拥有高的电子迁移率[4]和众多优秀的物理性质[5–8].对于石墨烯纳米带，更是由于其特殊的电子特性[9]和输运性质[10–13]而备受研究人员关注.由于石墨烯纳米带为有限宽度，所以其边界有一定的晶格边缘形状，根据边缘形状的差异，石墨烯纳米带可以分为锯齿型石墨烯纳米带和扶手型石墨烯纳米带.对于锯齿型石墨烯纳米带，不管其纳米带宽度怎样变化，其始终表现为金属型[14].与之不同的是，扶手型石墨烯纳米带由于其纳米带宽度的不同，可以分为金属型和半导体型，且其纳米带的宽度在调节其载流子极性中扮演着重要的角色[15].

本文主要研究在AB子晶格势、非均匀电势以及垂直磁场作用下扶手型石墨烯纳米带的能隙变化.如图1所示，该扶手型石墨烯纳米带的宽度为a0为晶格常数，N为在y方向的碳原子的个数.整个扶手型石墨烯纳米带被非均匀电势Ui等分为上下两个区域.在上半区域内电势为Ui=U，在下半区域内电势为Ui=−U.研究发现，对于不同类型的扶手型石墨烯纳米带，其能隙都会随着AB子晶格势的变化而规律性的变化.当同时考虑AB子晶格势和非均匀电势时，扶手型石墨烯纳米带的能隙存在打开与闭合的现象.最后，在纳米带上施加垂直磁场，两端电导表现出了有趣的量子演化行为.

图1 AB子晶格势、电势及磁场作用下扶手型石墨烯纳米带的示意图，其中空心圆代表A子晶格，实心圆代表B子晶格.该纳米带的宽度为(N−1)a0，晶格常数为a0，N为在y方向的碳原子的个数.B为外加垂直磁场，上半区域和下半区域的电势分别为U和−U

1 模型与方法

我们应用紧束缚近似方法，在子晶格势[16]、非均匀电势及磁场作用下，扶手型石墨烯纳米带的哈密顿量为：

第一项为最近邻跃迁项，t为不加外场调控时的最近邻跃迁积分.表示的是在i(j)点的产生（湮灭）算符，代表最近邻碳原子的位置.因为外加垂直磁场的作用，电子从j点向i点的跃迁过程中会产生一个附加相位，为，其中A=(0,−Bx,0)，φ0=/e[17].第二项给出了AB子晶格势对体系哈密顿量的贡献，其中Vi=νiV，νi=±1分别代表不同的子晶格.第三项为非均匀电势的贡献，其中电势与碳原子所在位置有关，在上半区域内其电势Ui=U，在下半区域内电势为Ui=−U.为了计算扶手型石墨烯纳米带的电子输运性质，我们应用了格林函数方程[18]去计算该系统的两端直流电导：

2 数值结果与分析

扶手型石墨烯纳米带由于其纳米带宽度的不同可以分为三种类型[20]，即N=3m，3m+1和3m+2，其中m是正整数，N为在y方向的碳原子的个数，如图1所示.当N=3m和3m+1时，该扶手型石墨烯纳米带为半导体型，当N=3m+2时为金属型.本文中，我们主要计算研究了在子晶格势、非均匀电势及垂直磁场的作用下，扶手型石墨烯纳米带的电子输运性质.

首先，研究在只有子晶格势作用时，即不考虑磁场及电势的情况下，扶手型石墨烯纳米带的能隙变化情况.如图2（a）所示，我们发现对于金属型的扶手型石墨烯纳米带，即图2(a)中纳米带宽度取L=，，在子晶格势 时，其能隙为零，但随着子晶格势 的增=11.93 nmN=3m+2=98V=0V大，其能隙逐渐增大，且呈线性增长.而对于纳米带宽度为11.68 nm，N=3m=96型以及=12.18 nm，N=3m+1=100的扶手型石墨烯纳米带，在子晶格势V=0时，其能隙不为零，但该类扶手型石墨烯纳米带的能隙也随子晶格势V的增大而呈线性增大，该线性关系最终与N=3m+2型的基本重合.当只考虑非均匀电势时（即子晶格势V=0,磁通φ=0），三种类型的扶手型石墨烯纳米带的能隙随非均匀电势U的变化如图2(b)所示.对于N=3m和N=3m+1的扶手型石墨烯纳米带，在逐渐增大U时，该纳米带的能隙刚开始变化较小，但到达某一临界时就随着非均匀电势的增大快速减小，最终趋于平缓.但对于N=3m+2的扶手型石墨烯纳米带，其能隙随着U的增大无单调的变化规律.当我们同时考虑子晶格势V和电势U（不考虑磁场）时，其能隙的变化如图2(c)所示.对于三种宽度类型的扶手型石墨烯纳米带的带隙随子晶格势V和电势U的变化关系，除了半导体型刚开始时为有能隙的半导体态外，其大体变化趋势基本和金属型的相同.

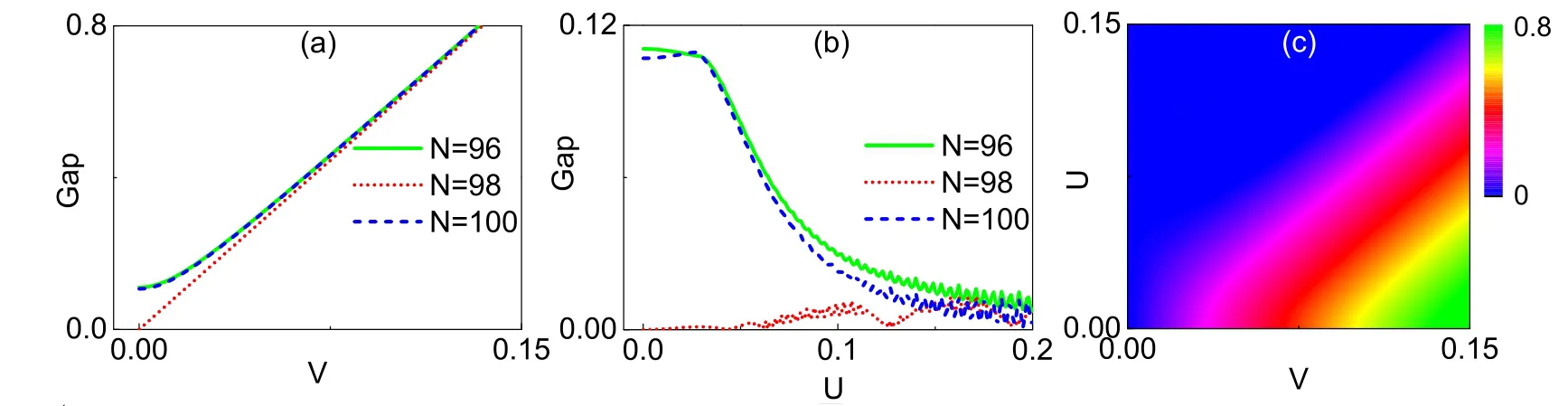
图2 (a)在子晶格势V作用下，三种不同类型的扶手型石墨烯纳米带的能隙随子晶格势的变化；(b)在非均匀电势作用下，三种不同类型的扶手型石墨烯纳米带的能隙的变化曲线；(c)在子晶格势及非均匀电势共同作用下带隙的相图，其中宽度为L=11.93 nm，即N=98

此外我们发现，对于N=3m+2的扶手型石墨烯纳米带，可以通过调节子晶格势V和非均匀电势U来实现能带的打开与闭合.如图3所示，当V=0和U=0时，N=98的扶手型石墨烯纳米带为无能隙的金属态.当V=0.041t，电势U=0.123t时，有能隙出现，该扶手型石墨烯纳米带变为了半导体态.当V=0.105t和U=0.123t时，该纳米带的能隙又消失了，纳米带又转变为金属态.

图3 宽度为L=11.93 nm，N=98的扶手型纳米带在不同的子晶格势V和非均匀电势U作用下的能带结构，其中(a)V=0，U=0；(b)V=0.041t，U=0.123t；(c)V=0.105t，U=0.123t

最后，我们还考虑了N=98的扶手型石墨烯纳米带在外加均匀垂直磁场作用下，其电子输运性质的变化情况.如图4(a)所示，当外加磁通取φ=0.008，且不考虑子晶格势V和非均匀电势U时，该扶手型石墨烯纳米带的两端电导值在零能附近为G=2e2/h，能隙闭合.当V=0.005t和U=0.05t时，零能朗道能级简并度被打破，零能朗道能级一分为二.同时由于非均匀磁场的作用，部分朗道能级向高能区移动，另外部分向低能区移动，这就导致了界面态的出现.当费米能穿过界面态时，系统的两端电导由2e2/h变成了4e2/h.当持续增大子晶格势，使其变为V=0.08t，电势仍为U=0.05t时，我们发现出现了明显的直接带隙，系统的电导也从G=4e2/h变为了G=0.这表明系统中发生了拓扑量子相变，系统由金属态变成了绝缘态.

图4 (a)-(c)宽度为L=11.93 nm，N=98的扶手型石墨烯纳米带在磁通取φ=0.008时的朗道能谱.图中各参数分别为：(a)V=0，U=0；(b)V=0.005t，U=0.05t；(c)V=0.08t，U=0.05t；(d)对应图(a)-(c)三种情况下的电导图

3 结论

我们研究了AB子晶格势、非均匀电势以及磁场作用下的不同类型的扶手型石墨烯纳米带的输运性质.我们发现对于三种扶手型石墨烯纳米带，其能隙都会随着AB子晶格势的增大而呈线性增大，最后三种变化趋势基本重合.对于半导体型的扶手型石墨烯纳米带，在只考虑非均匀电势时，其能隙会随一定范围内的该电势的增大而减小，最终会趋于平缓.对于金属型的扶手型石墨烯纳米带，其能隙随该电势呈不规则变化.当同时考虑非均匀电势和AB子晶格势时，对于金属型的扶手型石墨烯纳米带，可以通过改变电势和AB子晶格势的大小来实现拓扑量子相变.当此系统上再外加一个垂直磁场时，我们发现扶手型石墨烯纳米带的零能朗道能级会发生劈裂，同时有界面态出现，继续增大子晶格势，系统中出现带隙，这就导致零能处的两端电导从2e2/h到4e2/h再到0的演化，系统中出现拓扑量子相变.