双口碑效应下新产品扩散研究——以电影为例

张 旭，侯光明,2

(1. 北京电影学院管理学院，北京 100088；2.北京理工大学管理与经济学院，北京 100081)

1 引言

新产品扩散(New Product Diffusion)一词由美国学者Bass[1]在其构建Bass模型中明确提出，认为新产品扩散是在一定时间内，在大众传媒和口碑传播影响下，由率先采纳的少数消费者逐渐扩展为更多消费者的动态过程。新产品扩散理论反映了消费者群体行为的客观规律，推动了市场预测与营销策略相关理论与实践的发展。但该理论提出的时代背景在20世纪70年代，近年来科学技术与商业模式已发生深刻变革，尤其以客户为中心的体验经济已成为继产品经济和服务经济之后的主流经济形态，新产品扩散的管理情景需要与时俱进，面向体验经济的现实问题。

体验经济时代，消费者从注重产品或服务本身转变为注重整个消费过程的体验[2-3]。口碑，是消费者在消费体验之后对产品效能的综合评价[4]。在互联网时代，网络口碑已经成为消费者了解产品信息的重要来源，其传播对产品扩散产生重大影响[5-7]。尤其在移动社交网络环境下，企业在营销活动中需要精准识别用户，提高企业营销效果[8]。体验经济下的新产品扩散研究，聚焦体验经济情境下消费者群体扩散行为的客观规律，注重挖掘口碑对新产品扩散的影响，旨在充分利用口碑数据提升产品扩散预测绩效。

Bass模型提出后，学者们尝试从不同角度放宽Bass模型的基本假定，构建改进模型。Bass等[9]考虑价格与广告因素，将经典模型拓展为广义Bass模型。此外，其他学者从重复购买[10]、短生命周期[11]、生产限制[12-13]、产品迭代[14]等角度进行拓展，推动了新产品扩散理论的不断发展。

在口碑与新产品扩散相结合的研究主要集中在如下两方面：第一，口碑对新产品扩散影响的外部结果研究。Chung[15]以手机销售为例，研究了网络口碑对产品扩散速度、规模以及国际流动的影响。但该研究关注的口碑对产品扩散的影响结果，并未能在Bass模型框架下剖析口碑与产品扩散的内在关系。另外，Yan Xiaoming和Liu Ke[16]、Yan Xiaoming等[17]区分了正面和负面不同的口碑效应，研究网络口碑影响下供应端的生产策略最优化问题，但对需求端的产品扩散并无深入讨论。第二，口碑对新产品扩散影响的内在原理研究。Park和Hoon[18]提出了扩散过程中的第三种沟通渠道，即未采纳者之间的口碑传播，认为该渠道会使扩散形成指数增长态势。丁海欣[19]发现负面口碑对创新扩散比例和速度均有影响。Joo和Young[20]聚焦模仿效应中口碑传播的网络结构，并发现模仿效应系数值会随着网络密度降低而降低。但是，该角度研究并没有剖析口碑对扩散影响具体方式，更没有结合Bass模型基本理论假定，研究口碑对模型解的性质影响。

可见，现有研究已取得了丰富的研究成果，也为本文提供了良好的理论与方法参考。但是，外部影响的研究角度缺乏与企业实践中的市场需求预测相结合，而内部影响的研究角度则未能将正面和负面口碑合理嵌入Bass模型的建构。基于此，本文放宽Bass模型中关于口碑传播的基本假定，试图以模型解的性质分析来剖析口碑与新产品扩散关系的客观规律，并选择65部电影作为样本进行实证分析。本文选择以电影为例，主要有如下原因：第一，电影票房的扩散符合新产品扩散规律，基于Bass模型的票房预测有较好的拟合绩效[21]；第二，电影属于典型的体验型产品，口碑的在线评论对产品扩散过程影响明显[22-23]；第三，电影销售及口碑的相关数据完备且易得。

2 双口碑效应下新产品扩散模型

2.1 模型建立

2.1.1 经典BASS模型

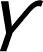
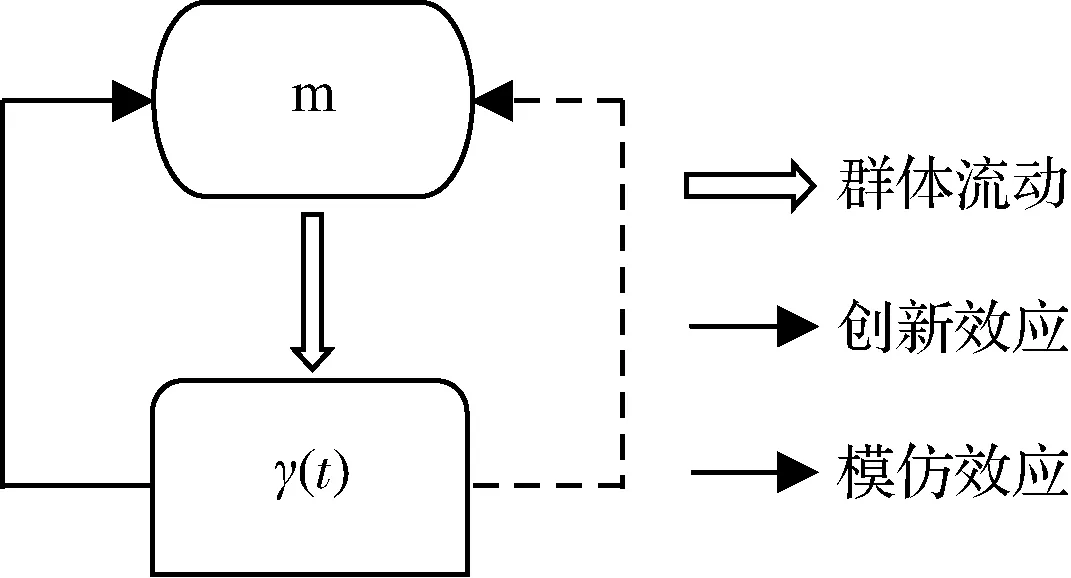
图1 经典Bass模型逻辑示意图

Bass模型的基本假设为式(1)，即潜在群体购买概率P(t)是购买消费群体占比的线性函数：

(1)

其中，参数p(>0)和q(<0)分别为创新效应和模仿效应影响系数。在式(1)的基础上，建立Bass模型的基本等式关系如下：

(2)

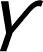
fBM(t)=(1-F(t))(p+qF(t))

(3)

其中，f(t)表示t时刻已购买人数占潜在群体比例，而F(t)则为截止t时刻已累积购买人数占比。求解此微分方程，可以得到F(t)和f(t)的解析解如下：

(4)

(5)

值得说明的是，下文研究中的参数符号表达与经典Bass模型一致，仅在下标处标示有所区别。

2.1.2 口碑规模效应下BASS模型修正

基于经典Bass模型的基本等式关系，可以分别从消费群体和购买概率两个角度进行模型修正。Sawhney和Eliashberg[24]提出消费者消费过程中决策和行动是两个相互独立的过程。基于此，从消费群体角度，本文提出了意向群体的概念，即由潜在群体m转换而来，形成了消费决策，但未能实际购买的消费群体，用字母N表示。

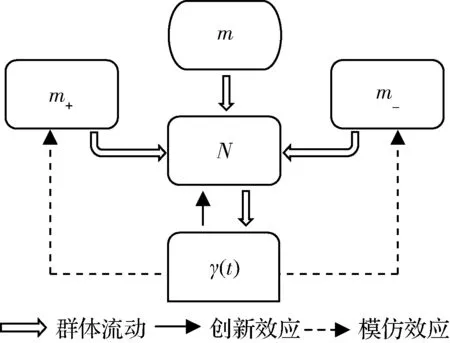
图2 口碑规模效应下新产品扩散逻辑示意图

口碑规模效应下新产品扩散模型(Quantity improved Bass model, QBM)如图2所示。在已购买者的口碑影响下，意向群体将是一个动态变化的过程。既有新增加的意向群体流入m+，也有改变消费决策的意向群体流出m-，即形成口碑规模效应，具体如下

N=m+m+-m-=(1+δ+-δ-)m=δm

(6)

其中，参数δ为规模效应系数。在此假定下，模型基本假定和基本等式修正如下：

(7)

(8)

进而求得口碑规模效应下的F(t)的解析解如下：

(9)

2.1.3 口碑比例效应下BASS模型修正

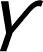
(10)

其中，参数θ为比例效应系数，q+和q-分别为正面口碑群体模仿效应系数和负面口碑群体的模仿效应系数。定义综合模仿效应系数qw如下：

qw=(1-θ)q+-θq-

(11)

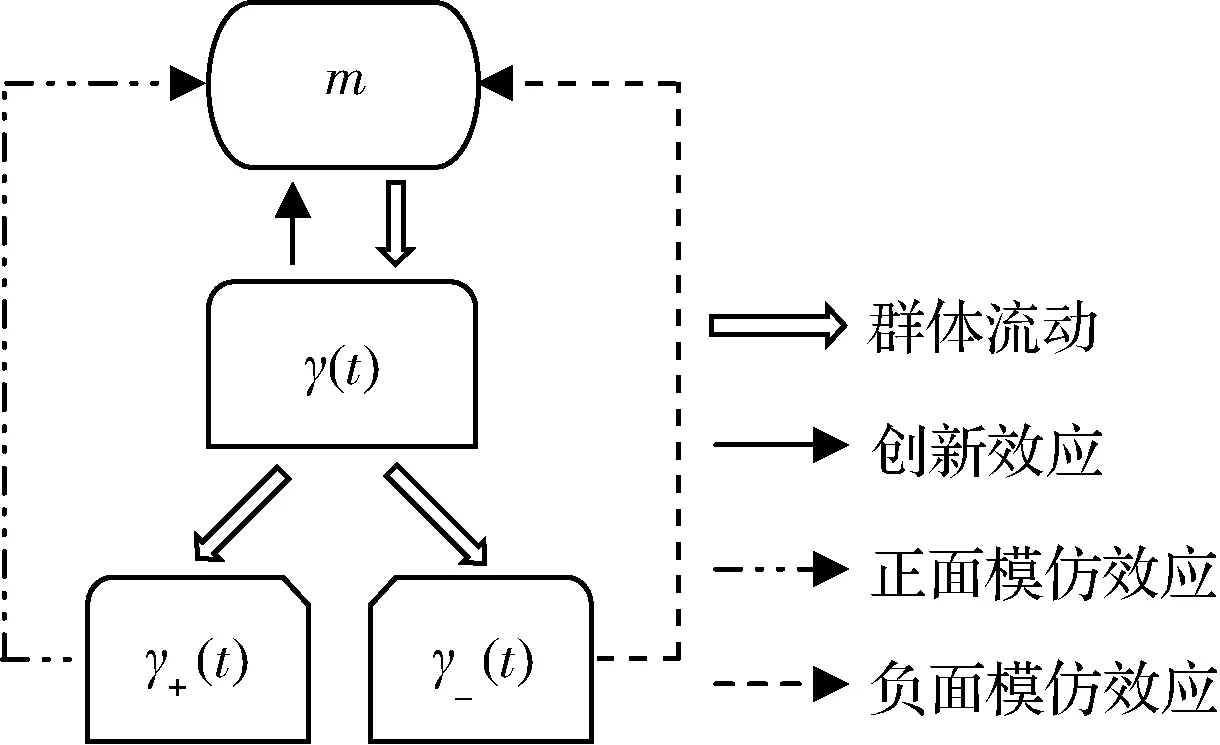
图3 口碑比例效应下新产品扩散逻辑示意图

因此，口碑比例效应下的基本假定和基本等式如下：

(12)

(13)

进而求得口碑比例效应下的F(t)的解析解如下：

(14)

2.1.4 双口碑效应下BASS模型修正

综合口碑规模和比例两方面效应，形成“潜在群体-意向群体-购买群体-正负口碑群体”的群体流动过程，建立双口碑效应下新产品扩散模型(Double improved Bass model, DBM)如图4所示。

图4 双口碑效应下新产品扩散逻辑示意图

持正面口碑的购买群体，通过正面口碑模仿效应影响购买概率决策的同时，吸引更多潜在群体成为该产品的意向群体；反之，持负面口碑的购买群体，则因负面口碑模仿效应导致意向群体的流失。综合两类效应，模型基本假定和基本等式如下：

(15)

(16)

进而求得双口碑效应下的F(t)和f(t)的解析解如下：

(17)

(18)

2.2 性质分析

在上文构建的DBM模型基础上，本文进一步分析规模效应系数和比例效应系数对产品扩散的影响。进行性质分析前，求解DBM模型相关峰值变量如下：

首先，将式(18)乘以m得到t时刻已购买人数SDBM(t)如下：

(19)

对式(19)求导，得到：

(20)

因此，在qw>p的前提下，令qwe-(p+qw)t-p=0，得到：

(21)

(22)

(23)

另外，将式(17)乘以m得到t时刻累积购买人数γ(t)如下：

(24)

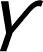
表1 DBM模型相关变量性质分析表

由表1可知，第一，峰值时间可以有效反映产品扩散的衰减情况，在双口碑效应下，群体流出越多，负面口碑比例越大，产品扩散的衰减会更迅速。此外，存在一定特殊情况，即某产品的综合模仿效应远远超过创新效应时，负面口碑比例越大，反而会形成一种舆论话题，引发消费群体关注，进而使产品扩散的衰减减缓。第二，峰值销量可以有效反映产品扩散中的最高销量水平，在双口碑效应下，群体流出越多，负面口碑比例越大，产品扩散的最高销量水平会降低。第三，峰值总销量反映的是产品在达到峰值之前的累积总销量，是全生命周期累积销量的最为重要组成部分，而在双口碑效应下，口碑规模效应与峰值总销量具有稳定的正相关关系，而口碑比例效应则与峰值总销量呈负相关关系。第四，累积总销量是产品扩散的最核心体现，命题4的两则命题是应用本文构建的双口碑效应下Bass模型修正，从理论上证明了口碑规模效应与累积总销量的正相关关系，口碑比例效应与累积总销量的负相关关系。

3 实证分析

3.1 回归模型建立

为了检验上文提出的双口碑效应下新产品扩散模型的实证效果，本文建立相应的回归模型。考虑到新产品扩散的S型非线性特征，本文采用Srinivasan和Mason[25]提出的针对新产品扩散的非线性最小二乘估计方法，将第t天的销量S(t)视作潜在消费群体m和第t天与第t-1天累积销量之差的乘积，如式(25)所示：

S(t)=m(F(t)-F(t-1))+ut

(25)

其中，ut为回归模型残差项。

由于实证以电影票房每日数据为例，以星期为周期的波动特征非常明显。为了剔除周期性因素干扰，本文加入周期性虚拟变量Dt，基于FBM(t)表达式，建立BM回归模型如式(26)所示：

SBM(t)=m(FBM(t)-FBM(t-1))(1+ηDt)+ut

(26)

其中，参数η为周期效应参数，而周期性虚拟变量Dt如式(27)所示：

(27)

同理，基于本文提出的FQBM(t)表达式，建立QBM回归模型如式(28)所示：

SQBM(t)=m(FQBM(t)-FQBM(t-1))(1+ηDt)+ut

(28)

其中，对于口碑规模效应模型中引入的规模效应参数δ，假定其为如式(29)的函数形式：

δ=(lnQ)E-μ

(29)

其中，Q为实际口碑评论数量，取对数以降低异方差影响，函数以lnQ为底是为了反映规模效应程度受口碑规模影响；E为产品实际口碑效价，反映产品口碑情感倾向，而μ为该函数中待估计的口碑效价参数，函数以E-μ为幂指数是为了反映规模效应方向受口碑情感倾向影响，即当E>μ时，δ>1，反之当E<μ时，δ<1。

另外，基于本文提出的FPBM(t)表达式，建立PBM回归模型如式(30)所示：

SPBM(t)=m(FPBM(t)-FPBM(t-1))(1+ηDt)+ut

(30)

其中，口碑比例效应模型中引入的比例效应参数θ，用产品负面口碑比例FU数据代替

θ=FU

(31)

最后，基于本文提出的FDBM(t)表达式，建立DBM回归模型如式(32)所示：

SDBM(t)=m(FDBM(t)-FDBM(t-1))(1+ηDt)+ut

(32)

其中，参数δ、θ、μ以及变量Q、E、FU均同上所示。

3.2 样本选择与数据来源

本文以电影为例，为了充分反映口碑对电影票房影响，从口碑好与差的两个角度分别选取2010至2014年间美国奥斯卡金像奖年度最佳影片提名电影和美国金酸梅奖最差影片提名电影作为研究样本，剔除数据缺失样本后，获得奥斯卡42部和金酸梅23部合计65部电影。

数据来源方面，样本电影的每日票房、总体票房、上映时间数据来自美国票房统计网站Box Office Mojo；电影口碑评分值、评论人数、负面口碑比例数据来自美国互联网电影资料库(Internet Movie Database, IMDb)。数据收集与整理主要采取抓取与解析网页的方式，收集数据截止时间于2015年11月16日。此外，值得说明的是，Bass模型基本假定要求新产品扩散以产品每期销量为基础数据，电影票房实质属于产品销售收入，是观影人次乘以电影票价后的结果，考虑到电影票价的相对平稳性和每日观影人次数据较难获取，本文模型均以电影票房为基础数据。

3.3 实证结果分析

3.3.1 拟合和预测绩效

为了从整体上全面分析构建模型的拟合情况，本文将回归估计得到65个样本电影的四个模型的拟合绩效指标即赤池信息量(Akaike information criterion, AIC) 和泰尔不等系数(Theil inequality coefficient, TIC)分别进行描述性统计分析，得到表2。其中，以BM模型为基准模型，令其指标数据为绝对数据，而其余三个模型则为相对数据，以反映构建模型的绩效改进。由于AIC越小，反映模型拟合越准确；TIC越小，表明模型预测绩效越高，预测误差越低。因此，当相对数据值越小，则表明模型相对于基准模型的绩效改进越好。由表2可知，绩效优化效果最佳的是DBM模型，其拟合绩效优化效果一般(<1%)，但预测绩效优化效果显著(>5%)。而PBM模型和QBM模型亦获得不同程度绩效改进，其中QBM模型的AIC相对数据为正，表明其并未能优化拟合绩效。

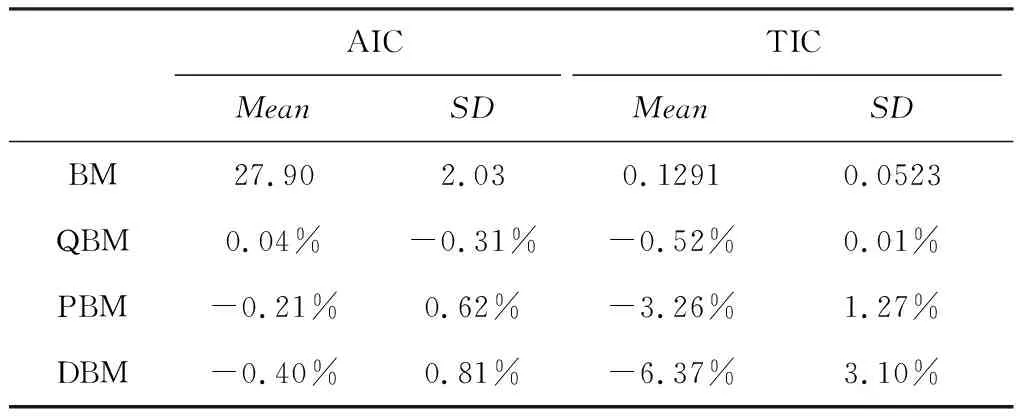
表2 回归模型绩效的描述性统计列表

由上可知，本文构建的DBM模型在拟合绩效和预测绩效方面均有所优化。为了反映DBM模型对于多样本的绩效表现，以AIC指标均值27.8为横坐标轴中点，以TIC指标均值0.12为纵坐标轴中点，建立直角坐标系下的66部样本电影绩效指标散点分布图，如图5所示。其中，浅灰色为奥斯卡电影而深灰色为金酸梅电影。四个象限样本占比依次为：16.9%、29.2%、24.6%和29.2%。虽然第Ⅱ象限占比最高，但是四个区域相差较小，散点分布相对均匀。另外，在口碑差异角度看，金酸梅奖样本电影主要分布在第Ⅲ和Ⅳ象限，而奥斯卡电影则分布较为分散。这说明DBM模型对于低口碑样本的预测绩效稳健性要强于高口碑电影。这可能的原因是，奥斯卡电影在提名或者获奖之后，往往会又有供给排片率的显著提高，对于未考虑奖项因素的DBM模型会造成绩效扰动。

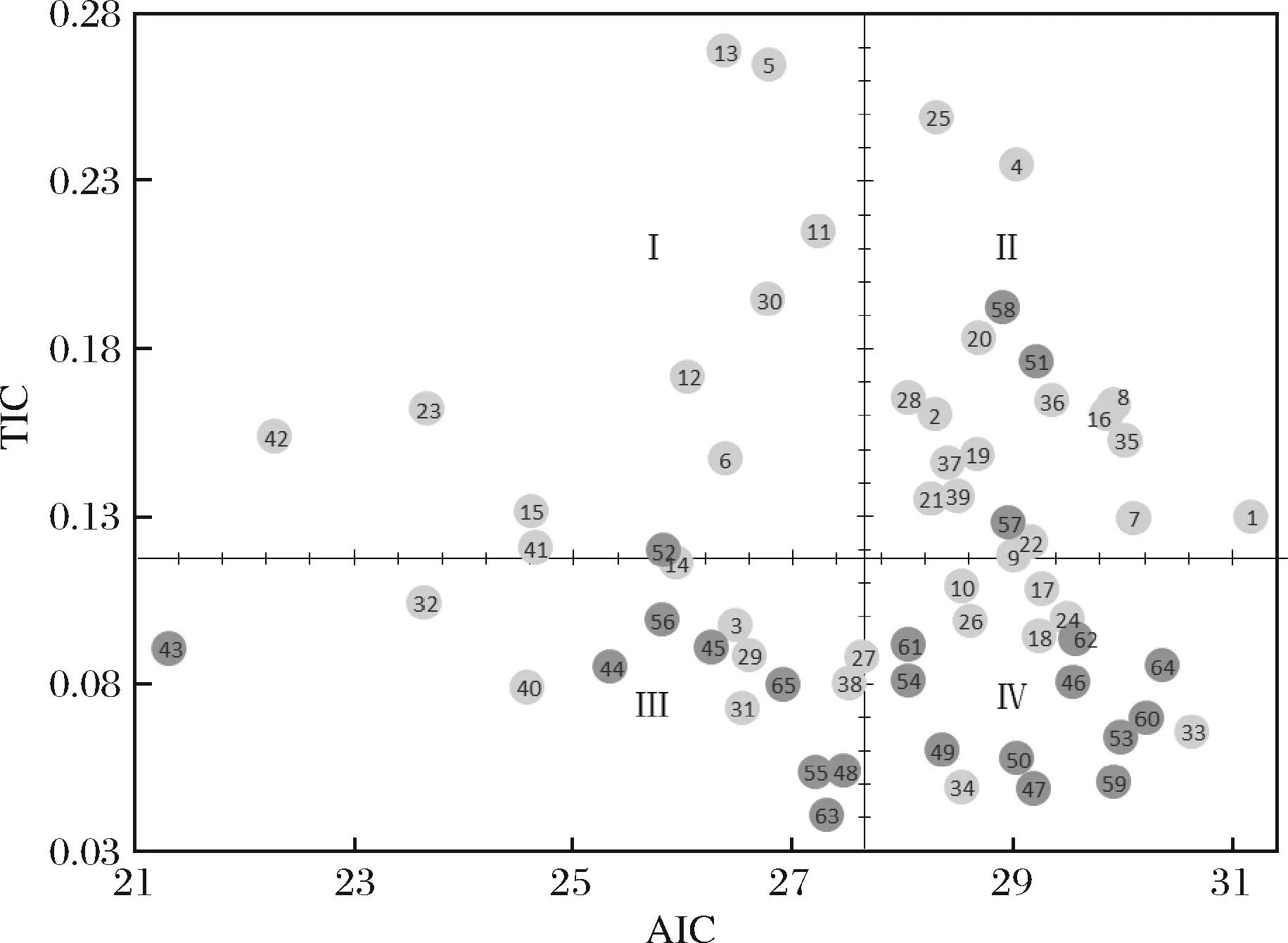
图5 基于DBM模型的样本电影绩效指标散点图

3.3.2 参数估计

本文将回归估计得到65个样本电影的四个模型的参数m、p、q形成描述性统计表如表3所示。值得说明的是，表中PBM和DBM模型的参数q值是依据表中q+和q-值，按照上文式(2.11)计算所得qw值，其他数据均通过回归估计汇总得到。

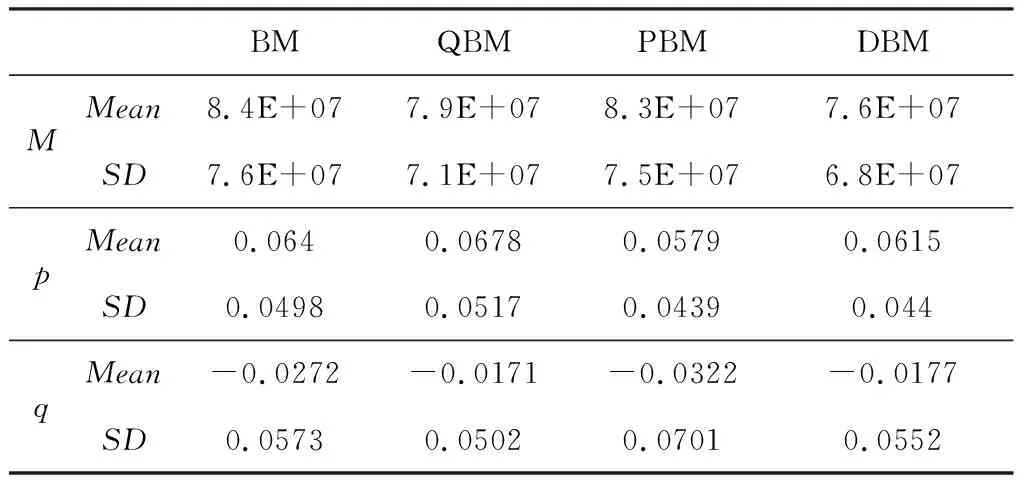
表3 回归模型参数估计的描述性统计列表

对于潜在群体参数m，相比较于BM和PBM模型，QBM和DBM模型的参数值较小。这是由于QBM和DBM模型引入了意向群体N，存在着口碑效应下的群体流动。因此，基于DBM模型，参数m在未考虑口碑效应的经典Bass模型中具有一定程度的高估。

对于创新效应参数p，相比较于BM和QBM模型，PBM和DBM模型的参数值相对较小。这说明基于DBM模型，创新效应在未考虑口碑效应下容易被一定程度高估，但并不明显。这也是由于模型构建时口碑效应的引入并未对参数p有直接影响。

对于模仿效应参数q，具有如下特征：第一，数值普遍呈现负值，这可能是因为高频次高波动性的日票房数据引入，对模型估计具有较强的扰动；第二，参数q数值为负故小于参数p值，因而样本电影的票房曲线主要是衰减形式，并不存在极值。值得说明的是，引入季节性虚拟变量后，电影票房周末极值则被季节性因素所解释；第三，DBM模型的参数值要大于BM模型，这说明如果不引入口碑效应，经典Bass模型的模仿效应容易被低估。

3.3.3 案例电影解析

本文选取三部案例电影进行分析。《盗梦空间》是奥斯卡2010年度最佳影片提名电影，IMDB评分8.7且全球票房达8.3亿美元，属于叫好又叫座的代表。《大力神》获金酸梅2014年度最差影片提名，IMDB评分仅4.2，北美票房不及2千万美元，是口碑差票房少的代表。《变形金刚4》同获金酸梅2014年度最差影片提名，虽然IMDB评分仅为5.8，但全球票房豪取11亿美元，是口碑差但票房好的代表。由图6可见，相比BM模型，三部电影的DBM模型能够较好拟合实际数据。

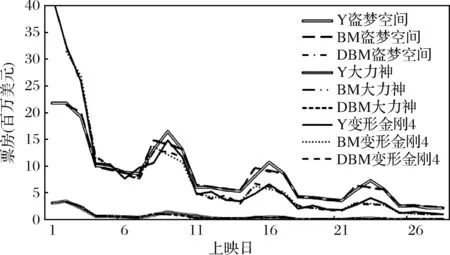
图6 样本电影DBM模型拟合曲线图

表4给出了样本电影DBM模型的全部参数估计值及绩效值，括号内为回归系数估计的标准误差。从拟合及预测绩效来看，DBM模型均有不同程度的绩效改进。从参数估计的显著性来看，DBM模型达到了较高的显著性水平。从参数估计值来看，其规律基本符合整体趋势，即经典Bass模型易造成潜在群体高估m值、创新效应p值高估和模仿效应q值的低估。

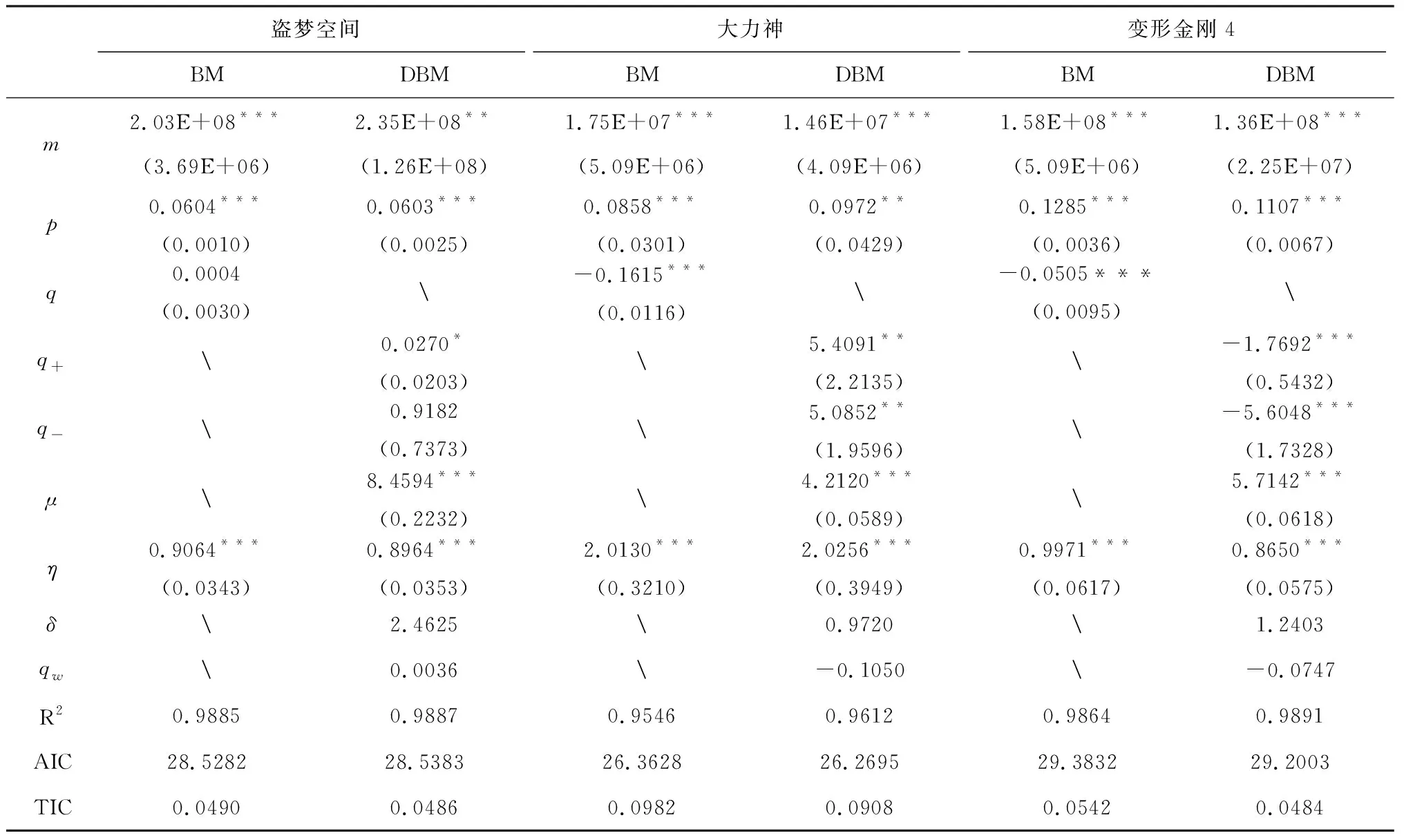
表4 样本电影DBM模型的参数估计列表

对于《盗梦空间》，其综合模仿效应参数qw为0.0036，虽然其值小于创新效应参数p值的0.0603，但为正值，说明该电影形成了口碑的积极传播效应，促使意向群体更加倾向于选择观看这部电影。此外，口碑规模效应参数δ为2.4625，显著大于1，说明在口碑规模效应下，意向群体的净流入增加，即更多观众成为了这部电影的潜在消费群体。由此，在这两方面的综合影响下，《盗梦空间》形成了“好口碑-积极扩散-群体增加-好口碑”的良好扩散循环，进而收获口碑与票房双丰收。

对于《大力神》，其qw值为-0.1050，绝对值要高于p值的0.0972且为负值，说明该电影的负面口碑造成了极为不利的口碑传播效应，大大降低了意向群体选择这部电影的概率和倾向。另一方面，口碑规模效应参数δ为0.9720，略小于1，说明意向群体出现了的净流出，即意向观众在口碑影响下逐渐减少。因而，在两方面综合作用下，《大力神》形成了“差口碑-急剧扩散-群体减少-差口碑”的恶性循环，从而票房迅速衰减，口碑差的同时票房成绩也一落千丈。

对于《变形金刚4》，其qw为-0.0747，绝对值低于p值的0.1107且为负值，说明该电影的负面口碑虽然具有一定程度的负面扩散效应，但是在前期宣传、广告等方面的影响下，意向群体的观影倾向并未显著降低。另外，参数δ值为1.2403，略大于1，说明意向群体形成了净流入，扩充了潜在消费群体。这一方面可能由于该影片强大的营销投入，另外也与该影片的动漫改编、续集电影等因素有关。总体在两方面作用下，《变形金刚4》在口碑不理想下实现了票房大卖。

4 结语

本文针对体验经济下新产品扩散问题，从口碑规模效应和比例效应两个角度，对经典Bass模型进行了拓展，构建了双口碑效应下新产品扩散模型。本文形成主要研究结论如下：第一，口碑规模和口碑比例效应是新产品扩散的两大口碑影响效应，可以对口碑与新产品扩散的关系给出理论解释。其中，口碑规模效应是指意向群体在已购买者的口碑影响下形成一个意向群体流入流出的动态变化过程，而口碑比例效应是指持负面口碑的购买者和正面口碑的购买者分别产生不同程度的模仿效应，对潜在群体购买决策概率产生影响。第二，通常情况下，在双口碑效应下，意向群体流出越多，负面口碑比例越大，产品扩散衰减会更迅速，最高销量水平会降低，累积总销量也会相应降低。第三，存在一定特殊情况，当产品的综合模仿效应远远超过创新效应时，负面口碑比例越大，产品扩散的衰减反而会减缓。第四，以电影为例的实证结果显示构建模型在拟合绩效和预测绩效均有较好表现。

本文的创新点与价值主要体现在如下三个方面：第一，将口碑因素纳入Bass模型，重塑新产品扩散流程。经典Bass模型没有关注口碑对模型的具体影响机理，忽略了负面口碑造成的需求丢失问题。本文梳理了“潜在群体-意向群体-购买群体-正负口碑群体”的群体流动过程，提升了关于正面和负面口碑协同影响的理论认识。第二，构建了双口碑效应的新产品扩散模型，并求得模型解析解。本文从口碑规模效应和比例效应两个角度，对经典Bass模型进行了拓展，给出了双口碑效应与新产品扩散的相关关系的理论证明，对于Bass模型在口碑渠道角度的发展具有一定的理论贡献。第三，基于美国65部电影实证证明，引入口碑数量、负面口碑比例等相关数据的模型具有明显的绩效改进。企业依据该理论模型，可以将口碑数据有效应用到市场需求预测中，提升口碑数据的应用价值，而基于口碑数据的需求预测，能够反映消费者体验的新产品扩散趋势，企业可以据此制定相应的用户体验提升策略和市场销售策略。

当然，本文研究也存在一定的不足。第一，理论构建方面，未来研究中会尝试将口碑动态性因素合理引入，放宽现阶段口碑规模和口碑比例的静态假定。第二，实证分析方面，本文仅仅以电影这一产品类型进行了实证分析，模型适用性有待进一步研究。电影属于文化创意产品，消费需求更多面向文化需求和情感需求，消费行为通过观影体验完成，受口碑影响更为明显。本文可能对此类口碑影响显著的产品适用性更明显。而大宗商品主要面向消费者的基本物质生活需求，除口碑之外，大众传媒也发挥重要影响。因此，未来可尝试电子产品等大宗产品类型，提升模型的稳健性。