基于Expectile回归的均值-ES组合投资决策

许启发，丁晓涵，蒋翠侠

(1. 合肥工业大学管理学院，安徽 合肥 230009；2. 合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009)

1 引言

现代组合投资主要通过定量化的模型与算法来确定最佳组合投资权重，实现期望收益既定条件下投资风险最小化。无疑，风险测度方法与组合投资模型等因素将关系到组合投资决策结果，对投资者、金融机构和监管当局的科学决策都将产生重大影响。为此，如何选择恰当的风险测度指标、构建相应的组合投资决策模型、采用合理的求解方法、改善组合投资绩效，是值得研究的重要课题。

在风险测度指标研究方面，经历了从矩风险测度到分布(尾部)风险测度的变化。Markowitz等[1]最早提出方差作为风险测度工具，使用了统计学中的二阶矩，开创了矩风险测度的先河。随后，文献中相继发展了半方差、下半方差等风险测度方法，克服了方差风险测度中将收益上升也视为风险的局限。然而，方差风险测度的理论基础是较为严格的正态分布假定，现实中往往难以满足(如：尖峰厚尾)，需要考虑更高阶的矩作为风险测度指标，如：Jondeau等[2]提出的偏度与峰度风险。与此不同，另外一些学者从损失分布特征的角度给出风险测度方法，代表性的当属Basel协议主推的VaR风险测度，参见Jorion[3]。Engle等[4]直接对VaR进行自回归，提出了CAViaR模型，用于动态VaR风险测度；刘晓倩等[5]使用加权复合分位数回归方法，估计动态VaR风险值；王璇等[6]基于二元模型，提出一种新的VaR风险度量模型，对组合投资风险进行分风险估计和总风险集成。但是，VaR方法不满足“一致性风险测度”标准中的次可加性等要求，并且无法衡量超过VaR部分的损失大小。为弥补VaR的不足，Artzner等[7]提出了ES(Expected Shortfall，也有文献称为CVaR)，并证明了ES较之VaR具有更优良的统计性质，可以很好地分散尾部风险。Taylor[8]提出使用Expectile估计ES，得到了更为准确的结果；Kuan等[9]提出了一个与CAViaR模型相对应的条件自回归Expectile(CARE)模型，用于估计动态ES；王鹏等[10]运用后验分析法，对比不同风险测度模型对ES风险指标估计的精确度差异；谢尚宇等[11]则在CARE模型中引入ARCH效应，建立了ARCH-Expectile模型；刘晓倩等[12]建立自回归加权复合Expectile模型，来评估ES风险大小；黄金波等[13]利用非参数核估计方法得到ES的两步核估计公式，建立均值-ES模型，同时实现对风险估计与组合投资优化。张冀等[14]将风险依赖、一致性风险度量与组合投资纳入到一个分析框架中，运用Copula函数预测组合投资ES风险。

在组合投资决策方法研究方面，可以概括为优化与回归两个方面。第一，基于优化算法的组合投资决策。Markowitz等[1]的均值-方差模型，主要通过二次规划方法结合KKT(Karush-Kuhn-Tucker)条件进行模型求解。而在高阶矩组合投资中，考虑到最大化期望收益(M)与偏度(S)、最小化方差(V)与峰度(K)，通过多目标规划方法求解M-V-S-K组合投资模型，详见Lai[15]、Sun Qian等[16]、蒋翠侠等[17]等的研究工作。对于均值-VaR与均值-ES(CVaR)模型，Rockafellar等[18-19]通过引入一个辅助函数，将其求解过程转化为一个线性规划问题，但涉及多维数学期望计算，存在“维数灾难”问题。第二，基于回归分析(包括：均值回归、分位数回归和Expectile回归)的组合投资决策。Fan Jianqing等[20]将均值-方差模型的求解过程转化为一个均值回归问题，不但避免了方差-协方差矩阵估计中的误差，而且得到更加稳健的组合投资效果。此外，该模型可以进一步扩展，通过引入LASSO惩罚实现金融资产选择，解决了基于方差风险的大规模组合投资决策问题。Bassett等[21]将均值-(C)VaR模型的求解过程转化为一个分位数回归问题；He Yaoyao等[22]引入权重约束，通过SCAD分位数回归，解决了基于(C)VaR风险的大规模组合投资决策问题。与组合投资决策的优化类求解方法相比，回归类求解方法一方面能够避免优化类求解方法出现的“维数灾难”问题，可以适应大规模组合投资决策需要；另一方面，能够更加准确地估计风险指标，得到更为稳健的组合投资效果。

迄今，尚无文献讨论使用Expectile回归进行组合投资决策分析。本文研究基于Expectile回归的均值-ES风险组合投资决策问题，主要在以下三个方面开展了创新性研究：第一，对均值-ES风险组合投资模型，利用ES与Expectile之间对应关系，将其求解过程转化为一个Expectile回归问题；第二，给出了均值-ES组合投资模型的Expectile回归求解新算法，提高了模型求解效率；第三，通过实证研究，从投资风险、投资绩效以及有效前沿等方面，对比了基于Expectile回归的均值-ES模型与均值-方差投资模型、均值-VaR模型的实证表现。选取沪深300指数中的5支行业代表性股票为研究对象，使用其2010年1月1日到2017年6月26日间日收益数据进行组合投资分析，实证结果表明：本文提出的组合投资决策方法，能够很好地分散极端情况下投资组合尾部风险大小，显著提高组合投资绩效。

2 传统组合投资决策与回归分析

2.1 均值-方差模型与均值回归

组合投资决策过程，旨在实现期望收益尽可能大、面临风险尽可能小，Markowitz等[1]通过均值-方差模型来实现这一思想。考虑收益为R=(R1,R2,…,RN)′的N个金融资产，组合投资权重向量为w=(w1,w2,…,wN)′，得到组合投资收益Rp=w′R，则经典的均值-方差模型可以表示为：

(1)

式中，∑=cov(R)为方差协方差矩阵，反映金融资产收益之间关系；约束条件w′1=1表示组合投资权重之和为1，1为由1组成的列向量；E(Rp)=r0表示给定组合投资期望收益为r0。

对于均值-方差模型，通常采用二次规划传统方法求解。但当金融资产数目过多时，不仅求解过程十分复杂，而且∑的估计存在较大误差。为了提高模型求解效率，Fan Jianqing等[20]将均值-方差模型转化为一个均值回归问题，不仅可以简化计算过程，而且能够降低计算误差。

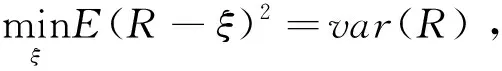
(2)

式(2)是实现将均值-方差模型的求解转化成一个均值回归问题的关键。对于约束条件w′1=1，可以进行展开、移项等操作，得到：w1=1-w2-w3-…-wN，将其代入式(2)并化简，可得：

s.t.E(Rp)=r0

(3)

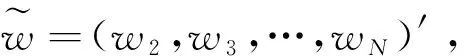
2.2 均值-VaR模型与分位数回归

VaR是指在某一置信水平100×(1-α)%下，投资者持有某项资产可能遭受的最大损失。记L=(L1,L2,…,LN)′为N个金融资产的损失，可以视为收益序列的相反数。Lp为组合投资资产损失，且有Lp=w′L=-Rp。这样，基于损失分布的VaR与基于收益分布的分位数之间存在关系：

VaR1-α(Lp)=-inf{x|Pr(Rp≤x)≥α}=-QRp(α)

(4)

式中，α∈(0,1)为与置信水平对应的分位点，inf{·}为下确界，Pr(·)表示概率。由式(4)可知，在给定置信水平下，VaR为收益序列α分位数的相反数。

对于损失L，其(1-α)分位数为下述优化问题的极小值点：

(5)

式中，损失函数ρ1-α(u)=u((1-α)-I(u<0))为分段线性函数，I(·)为指示函数。

考虑以VaR作为风险测度指标，依据组合投资决策思想，建立均值-VaR组合投资模型：

(6)

根据VaR与分位数之前关系，再结合式(5)与式(6)，可以将均值-VaR模型转化为：

(7)

依据组合投资权重约束条件w′1=1，有w1=1-w2-w3-…-wN，将其代入组合投资损失Lp，得到：Lp=w1L1+w2L2+…+wNLN，式(7)简化为：

s.t.E(Lp)=l0

(8)

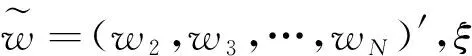
3 均值-ES组合投资模型与方法

3.1 ES风险测度

ES定义为损失超过某一阈值(VaR)的条件期望。对于组合投资资产损失Lp，在某一置信水平100×(1-α)%下，ES可以表示为：

ES1-α(Lp)=E[Lp|Lp≥VaR1-α(Lp)]

(9)

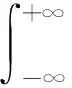
进一步，在给定组合投资损失Lp分布F下，可以计算出ES如下：

(10)

式中，F-1(·)为资产组合损失变量分布函数F的逆函数。可以看出，ES是由超出阈值VaR1-α的一组VaR进行加权平均所得。

3.2 均值-ES风险组合投资模型

对于N个金融资产，组合投资权重向量为w=(w1,w2,…,wN)′且满足w′1=1，在给定期望损失l0下，则均值-ES组合投资模型表示如下：

(11)

过去，对于均值-ES模型求解，通常使用拉格朗日方法，将有条件极值问题转化为无条件极值问题后，进而使用二次规划方法进行求解。为解决均值-ES组合投资模型求解过程中的麻烦，Quaranta等[23]和Rockafellar等[18]提出了一个线性规划算法。他们研究了一般分布条件下的ES风险大小，通过引入辅助函数，将以给定期望收益作为约束条件的组合投资决策模型，转化为线性规划问题来求解。不过，该方法涉及多维数学期望问题，往往存在“维数灾难”问题，并且计算结果不够精确。

为此，本文尝试使用Expectile回归，研究均值-ES组合投资模型求解方法，将其求解过程转化为一个Expectile回归问题，不但简化了计算的复杂程度，而且有利于均值-ES模型向大规模组合投资决策方面推广。

3.3 均值-ES模型求解

本节通过理论分析，论证了均值-ES模型求解问题可以转化为Expectile回归问题。通过优化Expectile回归目标函数得到Expectile，利用Expectile与ES之间对应关系，能够准确地得到最优投资组合的ES风险值。

3.3.1 理论分析

第一，在给定θ分位点处，Newey等[24]提出的Expectile分位数v(θ)为下述优化问题的极小值点：

(12)

式中，ρ1-θ(L-ξ)2=|θ-1|(L-ξ)2，θ∈(0,1)。式(12)表明，Expectile分位数为优化非对称平方损失函数的产物，这一结果与数学期望、quantile分位数相类似。实际上，数学期望为优化对称平方损失函数的产物，而quantile分位数为优化非对称绝对损失函数的产物。Expectile分位数具有与quantile分位数类似的性质，它可以完整刻画条件分布，而不局限于条件分布的均值。就统计属性而言，quantile仅考虑数据之间位置(或顺序)关系不考虑数据之间距离，而Expectile能够同时兼顾两个方面的信息。此外，二次损失函数为Expectile带来了计算上的优势、估计的有效性以及协方差矩阵的估计无需估计一个条件密度函数。因而，Expectile较quantile更具有优良性质。

第二，通过引理1与引理2，由Expectile分位数可以间接计算出VaR与ES(CVaR)。

引理1：对于给定的α∈(0,1)，记满足v(θ)=q(α)的θ为θ(α)，Yao Qiwei等[25]建立了θ(α)和q(α)的对应关系式如下：

(13)

式中，q(α)为α-分位数，可以看出，θ与α之间具有一一对应的关系。

引理2：对于组合投资损失随机变量Lp，具有数学期望E(Lp)，1-α分位点处的ES值ES1-α与θ分位点处Expectile值v(θ)存在关系：

(14)

式中，α∈(0,1)、θ∈(0,1)，且满足：F(v(θ))=1-α，本文使用的1-α与θ之间的对应关系详见Kuan等[9]在263页中给出的表1与图1；F(·)为Lp的累积分布函数。

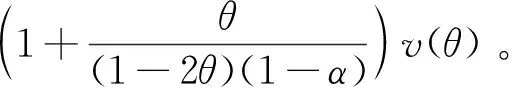
(15)

类似于前面的讨论，根据约束条件w′1=1，容易得到：w1=1-w2-w3-…-wN，进而可以将式(15)转化为：

s.t.E(Lp)=l0

(16)

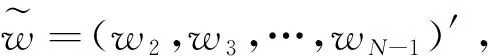
3.3.2 求解方案

上述理论分析的意义在于，将均值-ES组合投资决策转化为一个Expectile回归问题。本节基于Expectile回归，给出其求解方案。

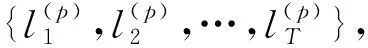
(17)

因此，基于Expectile回归的均值-ES模型求解可以概括为三个步骤：

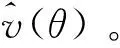
4 实证研究

4.1 数据选取与统计分析

综合考虑样本股票的行业代表性以及股票价格的持续可获得性，尽量保证股票分散于不同的行业，且在选定区间内不存在长期停牌甚至摘牌。故本文选取沪深300指数中的5支股票，分别为东阿阿胶、科大讯飞、五粮液、吉林敖东、中集集团，以其日收率为研究对象，同时将数据分为两个部分：样本内数据集和样本外数据集。其中，样本内数据区间为2010年1月1日到2015年1月5日，剔除非同步交易日和节假日，样本容量为N=1212，样本外数据区间为2015年1月6日到2017年6月26日，样本容量N=602。股票日收益率计算公式如下：

rt=100×(lnpt-lnpt-1)

(18)

式中，rt表示t期股票收益率，pt表示t期收盘价。本文数据来源于巨灵财经金融服务平台，所有运算均在R3.3.3软件中编程实现。

表1报告了样本内五支样本股票收益率的描述性统计，可以得到如下初步结论。第一，在样本内，除科大讯飞和吉林敖东外，其他三支股票的收益均为正值，分别为东阿阿胶0.00034、五粮液0.00023和中集集团0.00043。第二，所有股票收益的偏度均为负值，具有有偏性；峰度均大于3，说明5支股票收益分布具有比正态分布更肥的尾部，存在极端收益状态，这一结果由J-B检验得到了加强。为此，方差风险测度存在明显不足，需要考虑VaR、ES类尾部风险。第三，根据VaR和ES的定义，分别求得单支股票的风险值，发现五支股票的ES值均大于VaR值，表明：ES风险测度更为保守且能够较全面地衡量股票尾部风险。

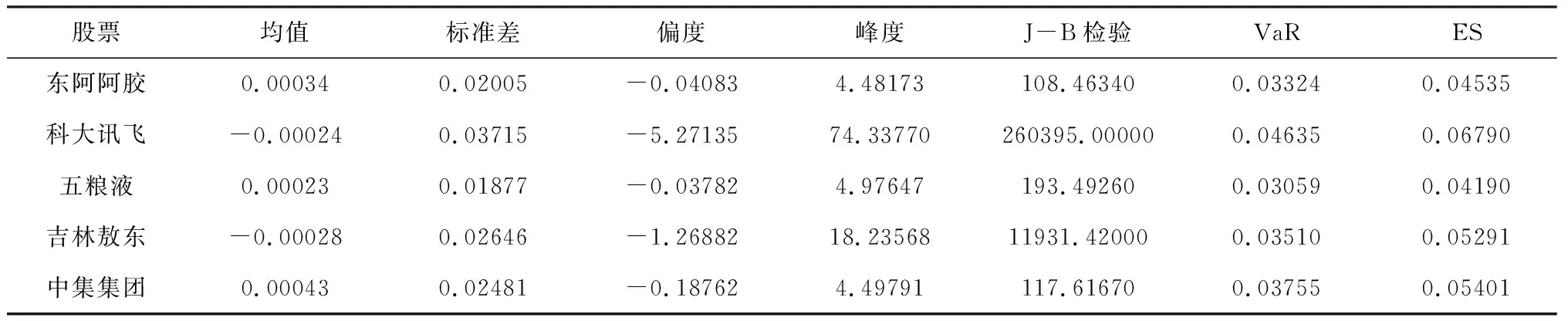
表1 股票收益率的描述性统计

4.2 组合投资分析

本文对均值-ES风险组合投资模型，使用Expectile回归方法进行求解，在给定期望收益约束条件下，计算损失序列尾部分布风险，并与均值-VaR组合投资模型、均值-方差组合投资模型进行比较，主要包括组合投资尾部风险、投资绩效以及有效前沿等三个方面的比较。

在进行Expectile回归时，为保证期望损失约束条件成立，对虚拟观测中的放大系数取足够大的值：κ=10000。在使用估计的Expectile计算ES和VaR时，需要考虑到θ与α之间的对应关系。引理1为此提供了一个基本关系，Kuan等[9]进一步通过Monte Carlo计算得到了特定分布(主要有：均匀分布、标准正态分布、t(30)、t(10)、t(5)、t(3))两者之间对应关系。本文采用Kolmogorov-Smirnov(K-S)检验判断组合投资收益是否服从某一特定分布，检验结果表明：由Expectile回归得到的组合投资收益分布与自由度为3的t分布相比较时，P值大于0.05，不能拒绝其分布一致的原假设。因此，认为其分布特征与t(3)分布没有显著性差异，本文关于θ与α之间的对应关系，可以使用Kuan等[9]第263页表1中最后一列(t(3)(%))的对应结果。

4.2.1 组合投资风险与绩效评价

为检验组合投资效果，需要考察其风险与绩效。以等权组合投资方案为基准模型，得到样本内组合投资收益均值为0.0004，同时设置VaR与ES风险的置信度为95%。利用前文给定的方法，得到基于均值回归的均值-方差模型(模型I)、基于分位数回归的均值-VaR模型(模型II)和基于Expectile回归的均值-ES模型(模型III)的样本内与样本外组合投资风险与绩效，结果如表2和表3所示。其中，表2中报告的模型I、模型II、模型III所得结果，都是以基准模型(等权组合投资方案)所得组合投资收益均值为给定期望收益。

表2 样本内组合投资风险与绩效评价

表3 样本外组合投资风险与绩效评价

就风险而言，样本内结果可以概括为以下结论。第一，以标准差(或方差)作为风险测度指标时，模型I、模型II和模型III所得投资组合的标准差分别为0.0175、0.0176和0.0176，均小于等权组合标准差0.0185，说明采用模型I、模型II和模型III可以达到分散组合投资风险目的。第二，以VaR和ES作为风险测度指标时，模型III的VaR和ES分别为0.0199和0.0123，均明显小于模型II、模型I以及等权组合投资方法，可见模型III用于分散组合投资尾部风险效果更优。

就绩效而言，本文考虑风险调整收益，采用Keating等[27]提出的Omega比率。由于Omega比率能够考虑到收益完整分布信息，从而比建立在收益矩(一阶矩、二阶矩)信息基础上的Sharpe比率、Sortino比率等绩效指标更为可靠。Omega比率是一个望大指标，数值越高意味着投资绩效越好，计算公式为：

(19)

式中，F(r)为收益率r的累积分布函数，r0为基准收益率。这里，将r0取值为0，意味着当收益率r大于0时，资产就会盈利；当收益率r小于0时，资产发生损失。从表 2可以看出，相比于等权组合、模型I和模型II，模型III所得组合投资的Omega比率最大，绩效更优。

结合样本外结果，可以发现：第一，本文基于Expectile回归的均值-ES模型(模型III)的样本外组合投资的风险与绩效表现良好，样本内风险与绩效的主体结论同时适用于样本外。第二，将模型I、模型II和模型III的样本内与样本外效果进行对比，可以看出，样本外的标准差、VaR和ES均大于样本内的结果，说明对于所有模型其样本内效果优于样本外表现，符合相应逻辑。

4.2.2 组合投资有效前沿

为进一步比较基于Expectile回归的均值-ES模型(模型III)与基于分位数回归的均值-VaR模型(模型II)、基于均值回归的均值-方差模型(模型I)的组合投资效果，研究其所得投资组合的有效前沿以及最小风险点。给定组合投资收益区间(-0.001，0.002)，将其等分为100个收益点，分别计算在每个收益点下对应风险值。在不同的给定期望收益条件下，能够得到一个最优组合投资以及相应的一组最优标准差、VaR与ES风险，从而得到三种不同的有效前沿表示方式，分别见图 1、图 2和图 3。在三个图中，分别报告了样本内数据的期望收益与标准差(方差)风险、期望收益与VaR风险、期望收益与ES风险之间最佳组合。样本外数据的结果与样本内相似，这里不作赘述。

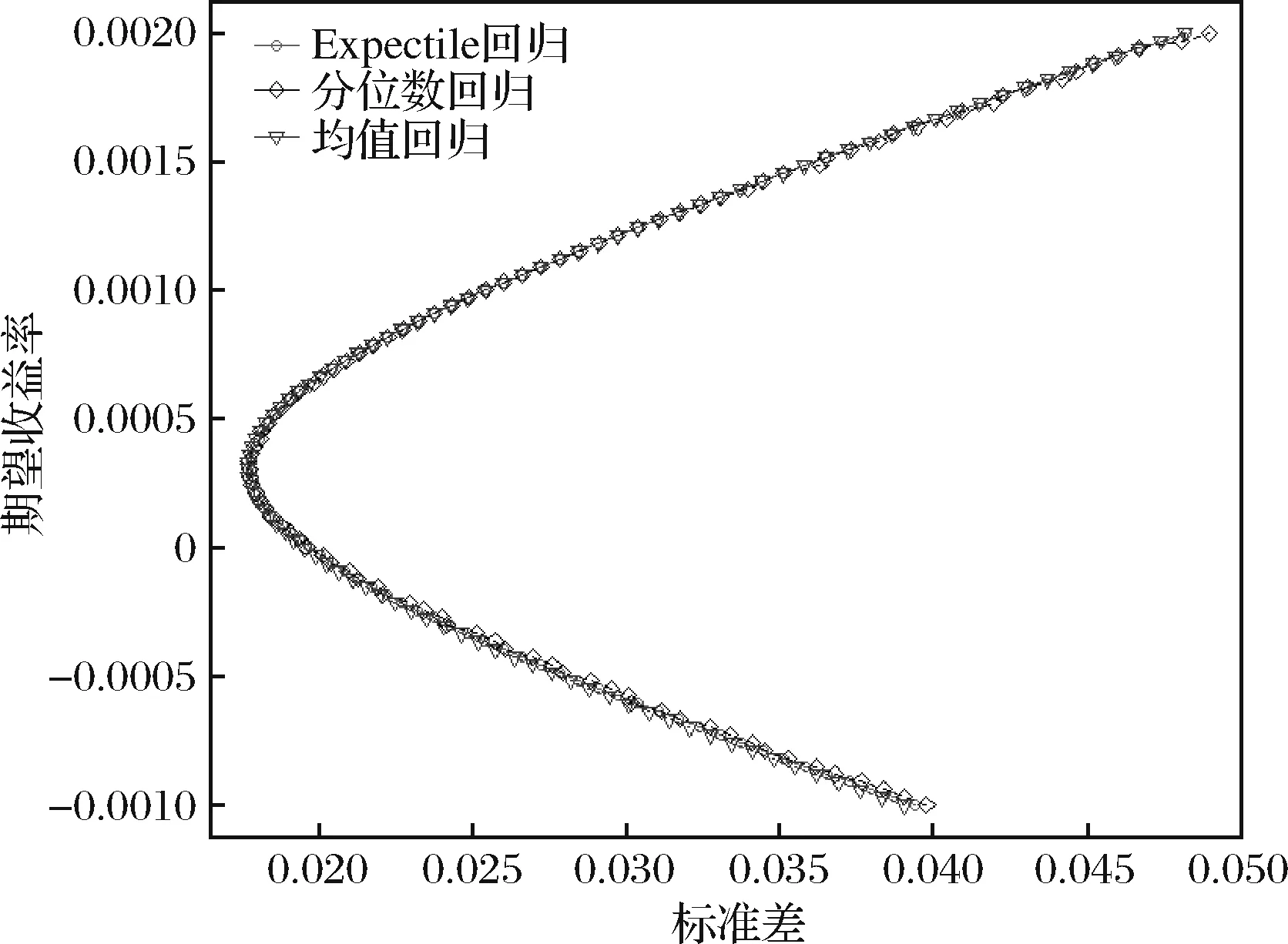
图1 组合投资有效前沿：收益-标准差

在图 1中，以标准差(方差)作为横坐标，可以发现：第一，模型I、模型II和模型III的有效边界存在差异，三种模型的有效前沿存在子集关系。其中，模型III是模型II的子集，模型II是模型I的子集。当选择置信度为95%时，模型I、模型II与模型III的有效前沿几乎重合。第二，以标准差(方差)作为风险测度指标时，在相同的期望收益下，模型I面临风险最小，这得益于模型I优化的对象为标准差(方差)。现实中，由于收益序列存在尖峰厚尾特征，不满足正态分布，使用均值-方差模型处理组合投资问题时，容易出现模型设定误差，低估组合投资风险。第三，就标准差(方差)最小风险点而言，三种模型的最小风险点恰好在期望收益率为0.0003时取得，得到最小标准差(方差)分别为0.0176(模型I)、0.0177(模型II)和0.0178(模型III)，验证了三种模型有效边界存在的子集关系。这一结果表明，期望收益率取0.0003时，三种模型均达到最优组合投资的临界点，过了该点即使再降低对期望收益率的要求，风险(标准差)也不会再降低。这一结论为投资者在风险可容忍范围内，权衡最佳期望收益提供了科学的参考依据。

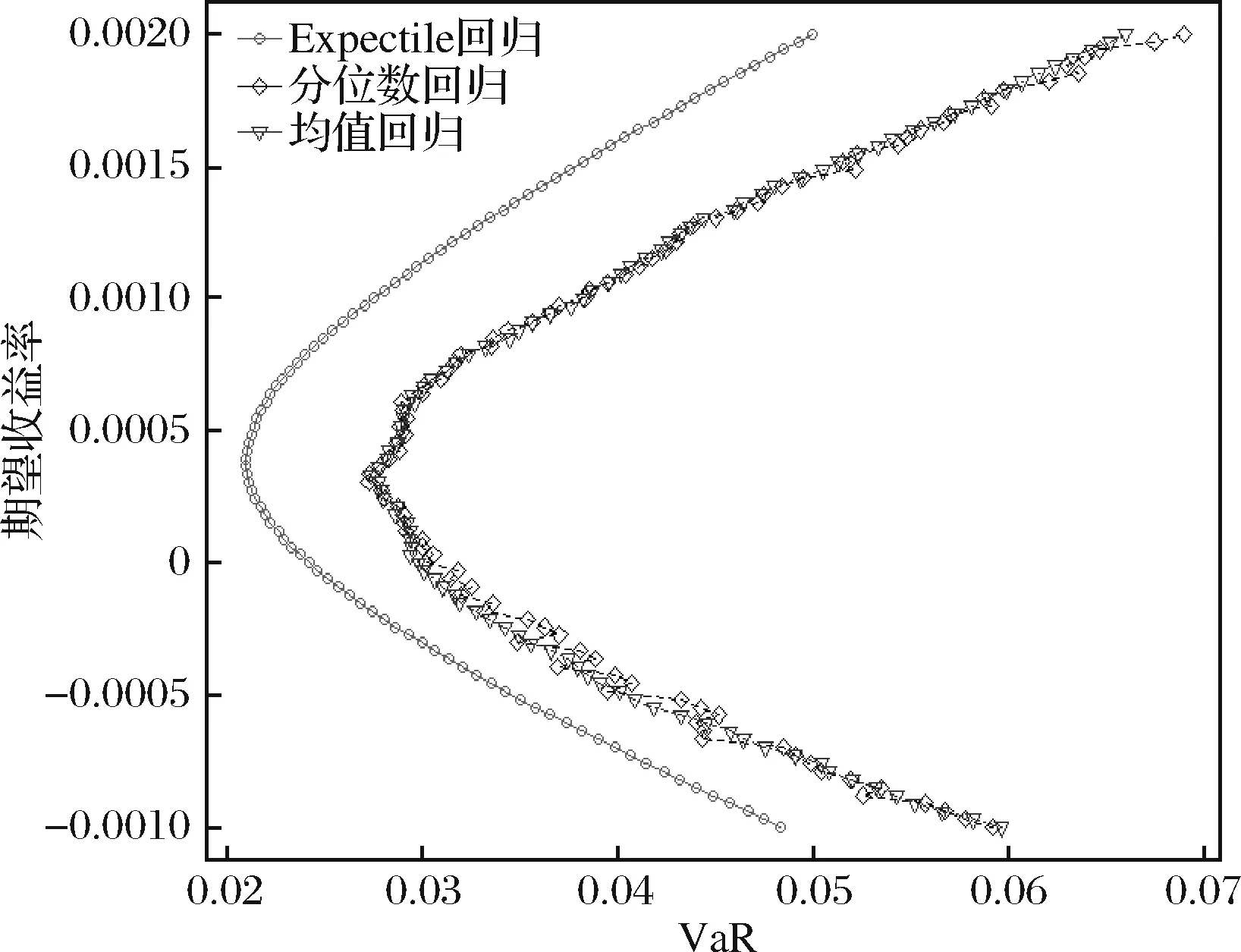
图2 组合投资有效前沿：收益-VaR

从图 2可以看出：第一，三种模型有效前沿存在子集关系，分别为模型I是模型II的子集，模型II是模型III的子集。第二，以VaR作为风险测度指标时，在相同的期望收益率条件下，模型III所得的组合投资的VaR值低于模型I和模型II，即前者所得组合投资风险更小，反映出模型III风险组合投资模型在分散尾部风险方面具有显著的优势，表明模型III比其他两个模型更为有效。第三，就VaR风险而言，三个模型的最小风险点有所不同。模型I在期望收益为0.0003时，取得最小风险点，最小VaR为0.0290；模型II在期望收益为0.0002，最小VaR为0.0299；模型III在期望收益为0.0002，最小VaR为0.0210。可见，当期望收益为0.0002时，模型III最小VaR小于模型II，且风险减小幅度达到29.76%，说明模型III在分散组合投资风险方面具有明显效果，有利于投资者改善最优组合投资效果。

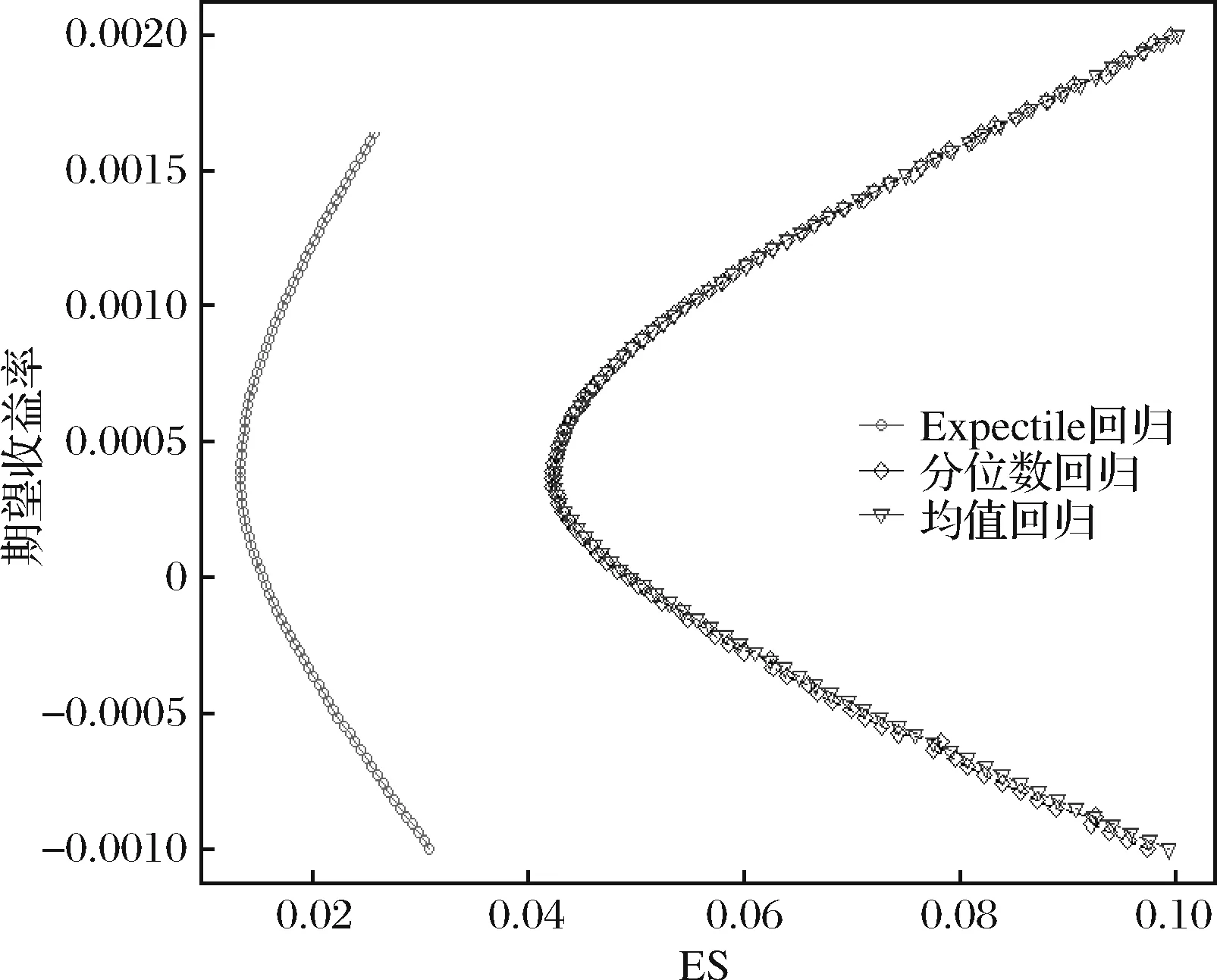
图3 组合投资有效前沿：收益-ES

由图 3可知：第一，以ES为风险测度指标时，三种模型有效前沿依然存在子集关系，模型I是模型II的子集，模型II是模型III的子集，意味着模型III所得有效组合投资范围更广。第二，模型III有效前沿位于最左边，面临ES风险最小，说明模型III可以很好的分散组合投资ES风险。第三，就ES最小风险点来看，当期望收益取0.0003时，三种模型均得到最优组合投资临界点，最小ES分别为0.0380(模型I)、0.0381(模型II)和0.0119(模型III)。此外，将图 2和图 3放在同一坐标系下，VaR有效前沿位于ES有效前沿的左侧，意味着在给定同一期望收益水平下组合投资的ES风险值大于VaR风险值。这一结果表明，ES风险测度在实践中相对保守，更合适作为组合投资风险测度指标。

5 结语

本文从回归分析的角度重新审视了均值-ES模型，将均值-ES模型的求解转化为一个Expectile回归问题并给出其求解算法。本文算法的主要优势在于能够避免传统方法在求解均值-ES模型时的复杂计算过程，而且便于在实际中进一步扩展与应用：监测和管理大规模组合投资。许启发等[28]使用Lasso分位数回归给出带有范数约束的高维组合投资模型求解算法，为从回归分析角度解决大规模组合投资决策问题提供了思路。为了实现从众多的金融资产中筛选出优质金融资产进行组合投资，未来可以将Lasso等变量选择方法引入Expectile回归，建立Lasso Expectile等回归方法，求解带有范数约束的均值-ES模型，完成大规模组合投资决策。

本文从组合投资的风险、绩效、有效前沿等三个方面，实证检验了基于Expectile回归的均值-ES组合投资模型(模型III)与均值-VaR模型(模型II)、均值-方差模型(模型I)的实证表现。实证结果表明：第一，就组合投资风险而言，模型III能够更好地分散风险，适合对尾部风险管理有高精准要求的市场参与者；第二，就组合投资绩效而言，通过Omega比率之间的对比，发现模型III绩效最优，处理组合投资决策问题更为恰当；第三，就组合投资有效前沿而言，在以VaR和ES作为风险测度指标时，模型III比模型I与模型II更为有效。