棉纤维细度检测技术综述

文/何晓峰 徐守东 刘从九

1 引言

棉纤维细度是衡量棉花品质的一个重要指标，在纺织工业上，它对成纱质量有较大影响。线密度是棉纤维细度的一种表述方法，即单位长度的质量。这种定义方法与常见的细度定义并不一致，一般细度是用几何尺度来定义的，产生这种现象的原因是，棉纤维的横截面形态不固定，主要有三种形态：扁平、椭圆（含其变种：腰圆、半椭圆）、近圆，且含有中腔，中腔大小不确定。因此，使用线密度定义棉纤维细度，就是为了测量方便。由于棉纤维细度与其成熟度密切相关，因此在讨论细度测量时，有时将不可避免要涉及到成熟度的测量。

2 棉纤维细度基准性的测量方法

棉纤维细度基准性测量方法来源于国际标准ISO 4912—1981，同时也是成熟度的基准测量方法，这是一种直接测量方法，测量原理扎实。测量过程如下：制作纤维横截面切片，经显微镜放大，在投影仪上输出到屏幕或者经CCD相机输出到计算机。该方法涉及的参数定义在下面给出，有些参数是ISO 4912—1981的定义[1]，有些是本文的引申。

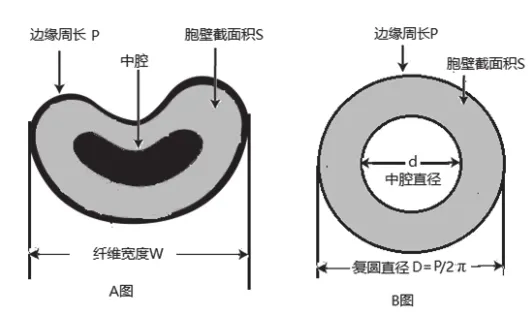
图1 棉纤维的原始截面（A）和复圆截面（B）

其中P——纤维原始截面的周长；S——纤维原始截面胞壁面积；W——纤维原始截面最大宽度，简称纤维宽度；D——复圆直径，定义为D=P/π；d——复圆内径，定义为d2=(πD2－4S)/π；T——纤维胞壁增厚度，定义为t=D－d；ρ0——棉纤维（胞壁）标准体密度，为常数1.524g/cm3；H——棉纤维线密度，H=ρ0S；Θ——圆度4πS/P2；M——棉纤维成熟度，定义为θ/0.577；K——成熟系数，定义为[（20t/D－1）]/3。

上述定义了棉纤维细度、成熟度的直接测量方法，只要做到对每一个纤维截面的周长、截面积的准确测量，就可以得到棉纤维细度、成熟度的准确结果。值得强调的是，棉纤维的细度是一个绝对量，只与其胞壁截面积大小有关；而棉纤维的成熟度是一个相对量，不仅与其胞壁截面积大小有关，还与其整体截面的大小有关。不过在早期使用投影仪技术的时代，若要直接测量棉纤维截面的周长、截面积还是很困难的，直到CCD器件出现，这一困难才得以克服。

3 棉纤维细度的图像测量方法

在上世纪70年代随着数字图像处理理论与基本算法的建立，后来CCD、CMOS成像技术的发展，将图像处理技术应用于棉纤维细度、成熟度的测量。上世纪80年代开始出现使用图像测量的相关文献[2,3]，并且持续到90年代末[4-7]，更多的文献不一一列举。总体而言，文献[3]给出的信息更全面，不仅涉及棉纤维，还涉及其他纤维，包括动物纤维、化学纤维、植物纤维等10多种纤维，并且对纤维截面形状分析的图像处理技术多有叙述。

这一阶段的研究特征是：CCD抓取棉纤维切片图像，将图像送入计算机处理，图像经过去噪、增强、阈值分割、二值化后，按照ISO 4912—1981的定义，计算棉纤维的成熟度。总的来说就是介绍了图像测量方法，而当时的数字图像处理技术、算法都是成熟的。在棉纤维品质检测方面，该方法的测量准确性取决于纤维切片质量。棉纤维切片传统制作方法，即用火棉胶封固纤维，用哈氏切片器制作切片，总有不少纤维截面是歪倒的，看不到纤维截面，不能识别；而且即便是可识别的纤维，也是根根相连、挤压、变形、遮挡。这两个弱点，造成一个切片中多根纤维不能被检测其细度或者成熟度。也就是说一个待测试样，只能正确识别部分纤维。根据笔者的实践，切片好的时候，一个切片有60%的纤维截面可识别；切片不好的时候，低于5%。一方面歪倒的截面与正常截面同时存在，另一方面纤维之间缺乏足够距离，使得计算机自动准确测量难以实现。不过传统切片制作方法产生图像技术应用的瓶颈，很快被一种新的切片制作方法所突破。文献[8]介绍了一种能够制作棉纤维优质切片的方法，它完全可以满足对棉纤维细度、成熟度的精准图像测量。与传统切片法相比，其特点是，每一根纤维的截面都是可见的，纤维截面之间都有距离，不是挤压在一起。该方法大致过程如下：将一小束纤维放入特制化学溶液里浸泡，纤维束在溶液作用下稍微发散，而纤维本身并不膨胀。然后让纤维束凝固、切片即可。该方法唯一的不足是切片制作时间过长，通常需要数个小时。尽管如此，该方法与计算机图像处理技术一道，实现了棉纤维细度、成熟度的基准测量方法，可以为标准棉样定标。

为能实现更快的测量速度，人们希望不需要制作切片，通过直接观察一根纤维的纵向特征，并测量某些参数后，计算棉纤维的细度、成熟度。由于将纤维稍做整理，直接固定在玻片上，容易操作、耗时少，在这种条件下就能测量出棉纤维的细度、成熟度，那就比制作切片观察截面方法便捷得多。文献[9]率先开始了这方面的研究，提出了纤维纵向测量细度、成熟度方法。该方法首先在显微镜下测量纵向棉纤维的平均宽度WM，并与AFIS测得棉纤维细度做相关分析，然后得到图像测量的细度。试验中采用了7个棉样，得到相关值R2=0.95。该研究的最大问题是没有意识到棉纤维不是圆柱体，因此它的宽度不会是它的直径；此外，棉纤维还有中空的中腔，因此宽度不能代表棉纤维的细度。这种间接测量方法，本质就是一种经验公式，可靠性只能限定在这7个棉样中。对于极限情况下，比如三种复圆直径相差较大的长绒棉、细绒棉、亚洲棉，能否保证经验公式仍然成立，还是需要有更多的支撑数据后，才能下结论。此外，虽然测量结果与AFIS结果高度相关，如果AFIS的结果本身就是错误的呢？后文将指出AFIS测量的一些问题。由于基于纵向纤维测量细度的巨大优势，所以这个方面的努力不会轻易停止，文献[10]提出了一种新的测量方法，它引入了一个叫作形状参数的量sp=（2P/A），定义纤维的比表面积ss=（4/WM）（WM是纤维平均宽度），并通过试验证明，形状参数sp与纤维平均宽度WM具有很好的相关性（R2=0.957）。从而得到结论：形状参数sp是纤维细度的指标。这个结论也是不可靠的，2P/A中的A是棉纤维的胞壁面积，可以看作是细度，而P是纤维截面周长，所以形状参数sp不是纤维细度指标。因此即便纤维平均宽度WM与sp相关性再好，它也不能作为棉纤维细度指标，因为棉纤维宽度不是棉纤维的细度这一结论，早就是共识。

4 棉纤维细度的气流仪测量方法

在棉纤维品质检测领域，棉纤维细度气流测量的研究，持续时间最长、投入工作量大、相关文献也最多。不莱梅循环测试有表现好的时候，也有完全失效的情况，这说明气流检测原理还需要更深入的研究。从气流检测细度的发展来看，可以分为E.Lord研究前、E.Lord研究后、二次测量法（或者二次压差法）。E.Lord之前的研究主要是用气流仪测纤维细度，既有试验研究，又有实用仪器。

4.1 气流仪检测原理

首先需要从E.Lord的研究展开，因为有关棉纤维的气流理论是他最先建立起来的，并且完成了奠基性的论文[11]。E.Lord的研究通过对当时的一种检测棉纤维细度仪器（仪器名字是Micronaire）的原理分析展开的，仪器的读数是线密度。E.Lord先对多孔隙介质渗流的基本理论进行了一个梳理，主要涉及泊肃叶、达西、苛仁纳-卡曼等人建立的公式。在一定试验基础上，他选择了苛仁纳公式作为测试原理：

K——苛仁纳常数；A——纤维阻流塞面积；Δp——纤维阻流塞两端压差；Q——气流流量；S0——纤维比表面积；μ——流体动力粘滞系数；L——阻流塞中纤维团的长度；ε——纤维阻流塞的孔隙率。

E.Lord并不能确认苛仁纳公式是否对棉纤维成立，因为该公式是基于球状细小沙砾为阻流介质建立的，它要求流体是不可压缩的，显然空气不满足这一条件；流体运动是层流，即流线是稳定的流动。为了保证试验尽可能接近或满足上述条件，他使用小压差（3mm水柱）做试验，研究了棉纤维比表面积S0、苛仁纳常数k、纤维阻流塞的孔隙率ε。E.Lord结合他人的结论，在假设棉纤维（包括中腔）整体体积度（密度的倒数）为0.75的情况下，得到如下关系：

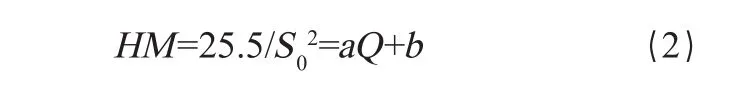
公式中的a、b是常数，Q是气流流量。该公式说明了两点：1）比表面积S0可以通过气流Q的测量得到；2）对棉纤维试样而言，它是细度与成熟度比的乘积。值得注意的是，该公式是基于棉纤维的体积度为某个值得到的，而且阻流塞中的纤维团比较松散。因此该公式是一个经验公式，使用条件比较苛刻，一旦测试条件发生变化，它就不一定成立了。

接下来，E.Lord研究了苛仁纳常数与纤维阻流塞的孔隙率的关系，他使用了5种纤维：棉花、羊毛、真丝、铜氨纤维、粘胶纤维做不同孔隙率的试验。从试验数据看，对于给定质量的纤维，除棉花外，其他纤维的体积可以用质量除以密度求得，再结合筒状纤维塞的面积A与纤维团的长度L，即可求出孔隙率。但这种方法不适用于棉纤维，因为棉纤维有中腔。E.Lord发现了苛仁纳常数k与纤维试样的孔隙率，有幂指数关系，即随着孔隙率的增加，苛仁纳常数会呈现指数增长。通过这种关系，修正后的苛仁纳方程如下：

其中α是与纤维类型有关的量，它是E.Lord通过试验得到的，对于棉纤维，其α=1.391；对于羊毛纤维，其α=1.253。该公式是通过对多种纤维试验后得到的结果，具有一般性。同时又有局限性，因为对不同的新种类纤维，需要自己试验测试其α值。

公式（3）在对纤维进行测量时，可以看到只有两个量是未知的，一个是比表面积S0，另一个是试样孔隙率ε。只要在对仪器进行标定时，先确定一个标准的孔隙率即可。以后仪器的使用，通过对试样量的限制，便能保证试样的孔隙率与标准孔隙率一致，进而得到待测纤维的细度。这种方法能很好测量实心纤维，甚至可以不改动仪器标定参数，就能实现不同种类实心纤维的细度测量。当然这需要事先知道待测纤维的体密度，才能计算相应的孔隙率。 文献[12]对9种规格涤纶、5种规格腈纶、1种规格丙纶做了测量，其方法是让所有试样的孔隙率与仪器要求孔隙率一致，试验结果非常好。该方法不但准确测量了圆截面的纤维，还能准确测量异形截面纤维，换算出其等效直径。就公式（2）、（3）而言，E.Lord当时认为不可能用它直接测量棉纤维细度或成熟度，必须先借助其他测量方法测量细度或成熟度中的一个指标，然后才能用气流仪测量另一个指标[11]。

4.2 二次测量法测棉纤维细度、成熟度

从公式（2）、（3）看，气流仪不能测量棉纤维的单项指标，如果一台仪器需要借助其他方法，才能实现测量，那是非常不方便的。许多研究者希望能够通过气流仪实现棉纤维细度、成熟度的直接测量，这一工作从上世纪50年代后期开始[13]到现在就没有断过，观点很多，不可能一一介绍，只能对一些有一定代表性的研究做简单评述。

文献[14]可能是最早提出二次压缩导致纤维截面变形的测量方法，即在松压下纤维保持原形态，有中腔；在紧压下纤维中腔消失。据此，试验建立压差/流量与棉纤维内外径的回归模型，进而求出棉纤维的几何细度。另有文献[15]认为在松压情况下，公式（3）中的比表面积S0应该用棉纤维的成熟度比来校正，因为成熟度比反映了纤维中腔的大小，得到的比表面积应该在紧压情况下，棉纤维被压扁中腔消失，比表面积是S2=2/r（r是纤维的等效半径）。经过松、紧压的两次测量，即可算出成熟度比M=(S2/S1)2；求出了成熟度，即可求出细度H=4πρ/S12。进一步解析可以得到与国际标准ISO/DIS 10306基本一致的棉纤维细度的二次压差解析式，它们的细微差别是，大量标准棉样测试后增加的对理论推导公式的修正项。文献[16]也是从纤维压扁视角来解决细度测量问题，在松压下，公式（1）中的比表面积是在紧压下，比表面积应该是其中C1、C2、β都是常数（参数β的产生缺乏足够支撑依据），然后结合公式（1）解析出纤维成熟度的表达式。文献[17]通过比较生硬的解析方法得到不同于公式（2）的新关系：

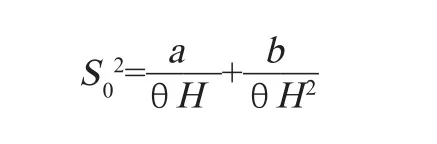
进而得到下面两个关系式

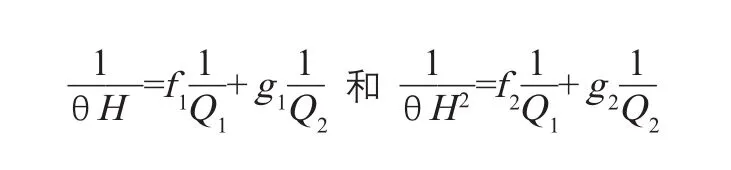
a、b、f1、f2、g1、g2是常数，可以通过多个已知棉样用气流仪来标定。那么基于这一对方程，通过测量松压流量Q1和紧压流量Q2，即可求出细度H和成熟度比M（0.577θ）。值得说明的是，虽然目前气流仪二次测量法是主流方法，但也有部分研究认为，一次测量就可以实现棉纤维细度测量[18-20]。

笔者经过大量的文献梳理（很多未在本文列出），发现气流仪测量棉纤维细度的文献多、观点多、方法多、预测方程多，而且都认为自己的结论是正确的，这本身就说明了气流检测的复杂性。如果一个问题很简单，能够一次性彻底解决，又何来这么多的解决方案呢？国内某企业在不长的时间内，申请了两个专利[21,22]，一个是二次压差测量法，一个是三次压差法。其实这么多的方法中，真有一个能经得起时间考验的方法就足够了。 遗憾的是，大量美棉样品的气流仪测试结果与标准方法测试结果的线性相关度，由1957—1988年的0.985～0.997陡降到0.4以下，迫使ASTM标准和ISO标准不得不在1997年停止执行。中国2006年开始发现规律混乱，气流仪数据与标准数据的线性相关系数，由1994年以前的0.887～0.927陡降到0.3以下[23]。美国农业部曾经做过两种气流仪（Statex公司和Shirley公司产品）7种棉样的细度测量比对试验[24]，试验结果偏差大。更严重的是，Shirley气流仪在3个样品上的结果大于Statex气流仪，在另4个样品上小于Statex气流仪，也就是说这两种气流仪不可能校准到一个水平上。总而言之，棉纤维细度气流检测原理是建立在多孔隙介质渗流的基本理论上的，虽然人们做了大量研究，对其规律也有了很深入的理解，但一个真正的关键性问题——棉纤维试样孔隙率与比表面积的内禀耦合问题，并没有解决。笔者认为，这个问题不解决，所有预测方程最多就是适应范围有限的经验公式，并随时存在失效的风险。

5 棉纤维细度测量方法

5.1 AFIS测量方法

AFIS是乌斯特公司生产的能够测量棉纤维成熟度和细度的快速检测仪器。现在能够查到的相关文献，大多是使用心得或者简单的测量原理说明。由于技术保密，乌斯特没有公开AFIS的检测原理，也看不到对其检测原理深入讨论的论文，如果一定要搞清楚它，则需要拆卸仪器、了解仪器内部结构、电路、传感器、检测重要的关键信号等，这显然难以实现。不过本文仍然想从有限的资料对其原理做一个探讨性分析。

根据AFIS附带的应用手册（2001版），AFIS首先将棉条用刺辊打散，然后用气流吸入一个通道，在通道里，棉纤维是单根状态。在气流的作用下，进入图2所示的一个专用的检测环境中。检测环境主要有两个部分，一个用于检测对象的识别，包括单纤维、棉结、碎片、灰粒，暂称为模块A；另外一个是散射模块，检测棉纤维的成熟度、细度，暂称为模块B。手册中表述“AFIS的光学传感器能够生成单纤维的阴影图像和散射图像（原话是shadow image and scatter image），这种技术能够测量纤维截面的周长和截面积……通过一种算法，根据纤维的形状和结构（原话是shape and form），即可测算出纤维的细度”。

图2 检测环境原理图

基于这么少的信息来推测AFIS的检测原理的确很困难。既然它能测量到截面积，根据前面公式H=ρ0S可得到细度；结合得到的截面的周长，轻松算出成熟度。问题是截面积和截面周长如何测出？显然阴影图像最多只能测出纤维的宽度，而绝不能测出纤维的截面积和截面周长，看来只能从散射图像来解读分析。光散射一般可以用来测量散射对象的尺度，比如红外散射测量雨滴大小；也可测量生物组织中某类物体的含量。一维散射图像通常是特征谱，二维散射图像是特征散斑。文献[25]使用了前向散射方法测棉纤维的细度，该试验的光源是氦氖激光，波长为λ=632 nm。通过对多种试样、多散射角的测量，得到多个特征图谱。其试验结论是，在10°～50°的散射角范围，散射特征图谱与棉纤维的细度、成熟度有很好的对应关系。小散射角度对应的是纤维截面积，大散射角度对应的是棉纤维的成熟度。不过对于细度很小、成熟度很高的测试样品，散射图谱特征不显著，意即散射方法失效。

假定AFIS的散射图像测量原理与上述一致，根据图2，透镜二产生的前向散射光输入到“散射模块”，透镜二前端的传感器，应该生成阴影原图像，可以识别被测对象究竟是不是单根的棉纤维。这是对AFIS检测原理的一个大致探讨性说明，这种猜测是说得通的。文献[26]采用图像测量方法，将其结果与AFIS的结果对比，得到两者测量棉纤维截面积的回归方程，回归系数为r=0.831。通过观察回归图形可以看到一个现象，在两端的值出现了发散。也就是说，当纤维截面积偏小或者偏大时，图像测量结果与AFIS的结果差异过大。由于通常认为图像测量是基准测量，这说明AFIS对细度过大、过小的纤维，测量不准确。也部分验证了文献[24]结论。另有试验采用中段称重法、氢氧化钠浸泡法来比对AFIS的细度、成熟度。结论是AFIS在150mtex～160mtex的细度范围，结果准确、可靠，而对于细度较大或者较小的纤维测量结果是，存在小的偏大、大的偏小问题。AFIS的成熟度与氢氧化钠浸泡法得到的成熟度偏差较大[27]。

5.2 CottonScope测量方法

CottonScope是澳大利亚BSC Electronics公司的产品，它能够快速准确地测量棉纤维的细度、成熟度。细度采用直接测量法，即将棉纤维切段、称重，然后抓取每根纤维切段的图像，采用图像测量技术，计算每根小段纤维长度，最后得到线密度。从测量原理看，CottonScope的细度测量，没有任何短板，下面就其技术特征进行全面论述。

我们采用CottonScope技术团队领导者Gordon对仪器描述的工作原理图[28]，见图3。棉纤维先经过一个专用的切段器，将试样切成0.7mm左右的小段（这个过程很快），这些小段纤维会落到一个精度为毫克级天平上，记下纤维质量，然后倒入图3上端的一个纯净水罐中。一个试样量有20000根左右的这样纤维切段。水罐中有一个搅拌器，将水中纤维打散。整个水路是连通的，在水泵的作用下，纤维进入一个细管，然后达到图像测量部分（由高速CCD系统构成），进行图像测量。测量过的棉纤维切段被拦截在一个过滤器内。所有纤维测量完毕后，从过滤器捞清即可。

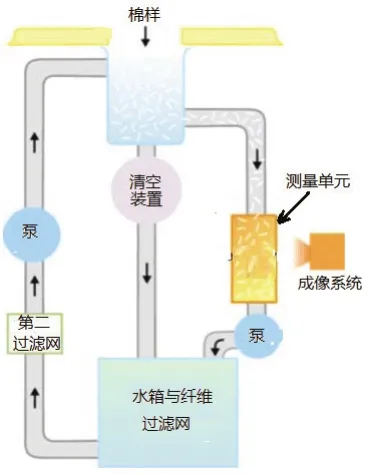
图3 Gordon对仪器描述的工作原理图

该测量仪器设计思路的确非常巧妙，操作简便。根据相关测试试验，其测量结果准确、快速[29]。从技术上看，笔者认为有几个关键点：（1）纤维是否完全打散。笔者从一个试验视频看到的情况是多数图像中，纤维是打散的，而且从图像处理技术角度来看，这些纤维已经足够散，完全可以逐根识别、测量。不过也确实看到一幅图像中有纤维团，没有打散开，当然对测量精度会有一定影响。（2）光学成像设计。从看到的纤维试样切段动态抓取的图像（见CottonScope网站https://www. CottonScope.com），以个人经验，其光学成像系统的光学放大率，应该在0.5～1倍左右。这种放大率已经是近显微成像水平，因此图像的景深非常小，保证所有纤维切段清晰成像，就不那么容易了，不过CottonScope做到了。（3）图像完整性。纤维在测量单元是运动的，如何保证每幅图像既不漏检纤维、也不重复计入同一根纤维，这不好处理。一般有两种方案，一个是让图像测量单元处的水流速度与CCD抓图间隔保持同步，该方案的难点在于如何保证系统长时间可靠运行。因此基于闭环的流速传感器、水泵转速调节控制系统必不可少。另一个方案采用连续图像流处理技术，即通过连续图像来判断水流速度，然而由于纤维是运动的，如果纤维的姿态在不同的图像帧中变化太大，会大大增加软件的处理难度，唯一的好处是保证了图像获取与水循环系统的无关性，增加了系统的可靠性。由于CottonScope采用的是称重法测棉纤维细度，因此尽管其测量速度很快，可棉样需要在标准温湿度环境下平衡很长的时间，以确保称重的准确性。CottonScope的长处就在于极大简化了操作强度，这也是它具有极大吸引力的地方。

6 结论

本文介绍了目前主流的棉纤维细度测量方法或技术，以及各自的特点。图像法是操作繁琐的、测量原理扎实的直接测量方法；气流仪方法是操作简便的、测量原理不清晰的间接测量方法；AFIS是操作简便的、测量原理未被揭示的间接测量方法；CottonScope是操作简便的、原理扎实的直接测量方法，也是目前最值得首选的仪器。未来仪器发展趋势应该是将各种优势技术结合，要同时保证测量准确性和操作快速便捷性，而且测量原理一定要清晰，这样的仪器才有市场，才有生命力。