矩阵方程AXBT+BXAT=F的参数迭代法

张 洁,唐 嘉,马昌凤

(福建师范大学 数学与信息学院,福建 福州,350117)

矩阵方程经常出现在许多应用领域,例如控制理论、系统理论、 稳定性理论,以及模型还原和图像处理等。由于矩阵方程广泛的应用背景,使得它吸引了许多研究者的广泛关注。求解矩阵方程的方法有很多,例如参数迭代算法、共轭梯度迭代算法、矩阵分解法等,其中参数迭代法倍受关注[1-3]。 在过去的几十年,线性矩阵方程得到了广泛的研究[4-14]。

考虑控制理论中提出的矩阵方程

AXBT+BXAT=F

(1)

其中A,B,F∈Rn×n是给定的矩阵,X∈Rn×n是待求的未知矩阵。方程(1)有唯一解X当且仅当(B⊗A+A⊗B)的特征值不为零。若A和B均为可逆矩阵,则矩阵方程(1)等价于

(A-1B)X+(A-1B)T=A-1FA-T

(2)

方程(2)有唯一解X当且仅当A-1B没有相反的特征值。特别地,当A,B是对称正定矩阵时,(B⊗A+A⊗B)也是对称正定矩阵,所以矩阵方程(1)有唯一解。

1 参数迭代法与收敛性分析

当矩阵方程(1)有唯一解X*时的参数迭代法以及最优,近似最优参数的选取问题[3]。选取实数α≠0,使αA-1B-I为可逆矩阵,令

C=(αA-1B-I)-1(αA-1B+I)=I+2(αA-1B-I)-1

(3)

那么,C-I=2(αA-1B-I)-1也是可逆矩阵,且有

αA-1B=(C-I)-1(C+I)

(4)

方程(2)两端乘以α,再将(4)代入可得

可得

X=CXCT+Y0

(5)

因为α≠0且C-I可逆,所以方程(5)与(1)等价。根据方程(5)建立参数迭代格式

Xk+1=CXkCT+Y0,k=0,1,2,…

(6)

用拉直算子将式(6)转化为列向量形式

vec(Xk+1)=(C⊗C)vec(Xk)+vec(Y0),k=0,1,2,…

(7)

式(7)是一阶线性定常迭代格式,它的迭代矩阵为C⊗C,且有ρ(C⊗C)=ρ2(C)。

有如下的收敛性定理。

定理1[3]对于任意的初始矩阵X(0),格式(6)收敛的充要条件是ρ(C)<1。

当A,B是可逆矩阵时,设C的任一特征值为λc,对应的特征向量为x,则有Cx=λcx,即 (αA-1B-I)-1(αA-1B+I)x=λcx,于是α(λc-1)A-1Bx=(λc+1)x。因为A-1B可逆,所以λc≠-1。于是有,

(8)

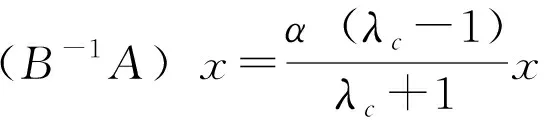
(9)

(10)

即C的特征值可由B-1A的特征值表示出来。

定理2[3]设A,B可逆,对任意的初始矩阵X0,格式(6)收敛的充要条件是

(11)

推论1 设A可逆,且B-1A的特征值的实部大(小)于零,则对任何负(正)数α,格式(6)收敛。

定理1表明,只要选取适当实数α，使得ρ(C)<1,格式(6)就能够收敛。需要研究的问题是：如何选取实数α,才能使格式(6)收敛最快,即使ρ(C)最小。

2 最优参数的选取

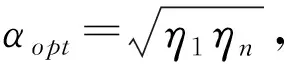
证明 因为B-1A=B-1/2(B-1/2AB-1/2)B1/2,即B-1相似于B-1/2AB-1/2,而B-1/2AB-1/2合同于A,所以B-1A的特征值为正数。根据定理1,对于任何负数α,格式(6)收敛。B-1A的特征值排序为η1≥η2≥…ηn>0,由式(10)可得

(12)

(13)

ρ(C)的最小值只能在g1(α)和gn(α)的交点处取得。令g1(α)=gn(α),可求得

(14)

确定格式(6)的最优参数时,需要计算B-1A的最大和最小特征值。为了避免计算B-1,下面讨论格式(6)的近似最优参数的选取问题。

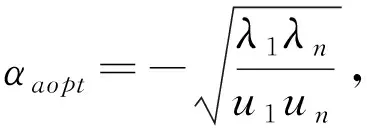
证明 设A和B的特征值分别为

λ1≥λ2≥…≥λn,u1≥u2≥…≥un。

根据广义特征值的极值原理,由式(8)可得

(15)

(16)

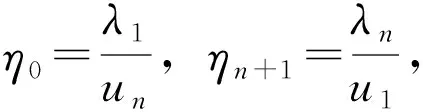
(17)

易见ρ(C)≤q(α),欲使ρ(C)最小,只要q(α)最小即可。类似于(14)的推导,可得

(18)

3 迭代校正法

迭代法的收敛性可以通过迭代校正得到提高。考虑矩阵方程(1),记g(X)=AXBT+BXAT。此外,设矩阵方程的唯一解为X*,X1,X2,…,Xm(m>1)为X*的不同近似矩阵,且g(Xi)≠F,(i=1,2,…,m)。利用诸Xi提供了的信息构造矩阵X,使满足

(19)

称矩阵X为方程(1)关于X1,X2,…,Xm(m>1)的校正解,确定X的过程为校正过程。整体校正模型(WMC)[4]如下

(20)

所谓整体校正,是指Xi的每一个元素对X的对应元素的贡献比例相同。

将校正过程施加于任何一种求解矩阵方程(1)的迭代格式,可以改善原格式的收敛状态。设求解矩阵方程(1)的单步迭代格式为

Xi=φ(X(i-1)),i=1,2,3,…

(21)

改进格式(21)为

(22)

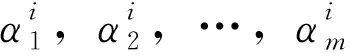
一方面,当格式(21)收敛时,格式(22)必定收敛。进一步,当第i次校正过程的整体缩减系数αi<1时,格式(22)比(21)收敛的快。另一方面,当格式(22)不收敛时,由于αi<1几乎对所有i成立,所以格式(22)也能收敛。

4 参数迭代加速算法

下面讨论关于迭代格式(6)的加速方法。

令X0=Y0,则根据数学归纳法,迭代格式(6)可写为

(23)

当ρ(C)<1,则

(24)

其中X*是原方程的精确解。

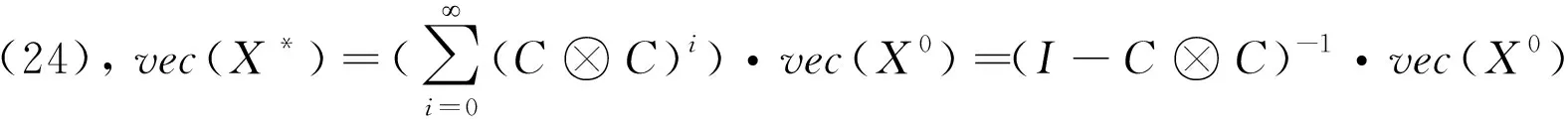
采用级数(24)的部分和逼近X*时,为了加速收敛过程,可取该级数的前2{k+1}项构成的部分和进行迭代计算,即

于是,可得部分和迭代格式

(25)

5 数值实验

给出两个数值例子来验证对其最优参数选取以及对应迭代校正算法和加速算法的有效性。所有的实验都是在如下环境中实现的：Windows 10系统,Matlab R2015a。

例1 考虑矩阵方程AXBT+BXAT=I,其中

通过计算得到矩阵A,B的特征值

λ1=0.4903,λ2=1.9128,λ3=9.5969
u1=2.1981,u2=3.5550,u3=5.2470

B-1A的特征值为η1=2.0825,η2=0.2029,η3=0.5195。

由(14)和(18),可得αopt=-0.6501,αaopt=-0.6387。

根据以上的算法,得到矩阵方程的解和停止准则为10-10。对α取不同的值,则数值结果如下。从图1和图2可以看出参数迭代法使用最优参数(αopt=-0.6501)和近似最优参数(αaopt=-0.6387)与加速算法的比较。从表1，可以看到参数迭代法(6)和迭代校正法(22)的比较。 同时,可以从表2看到参数迭代法(6)和加速算法(25)的比较。在经过迭代校正和加速后，易见(6)的收敛性大大地提高了。

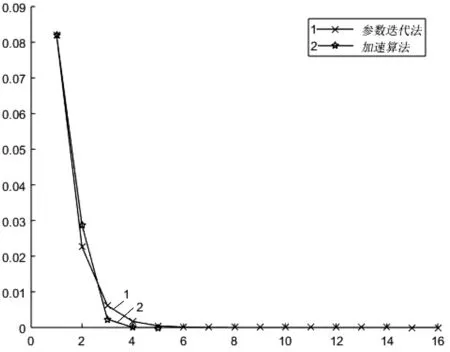
图1 例1中的迭代次数与误差(αopt=-0.6501)Fig.1 The iterations and errors for Case 1

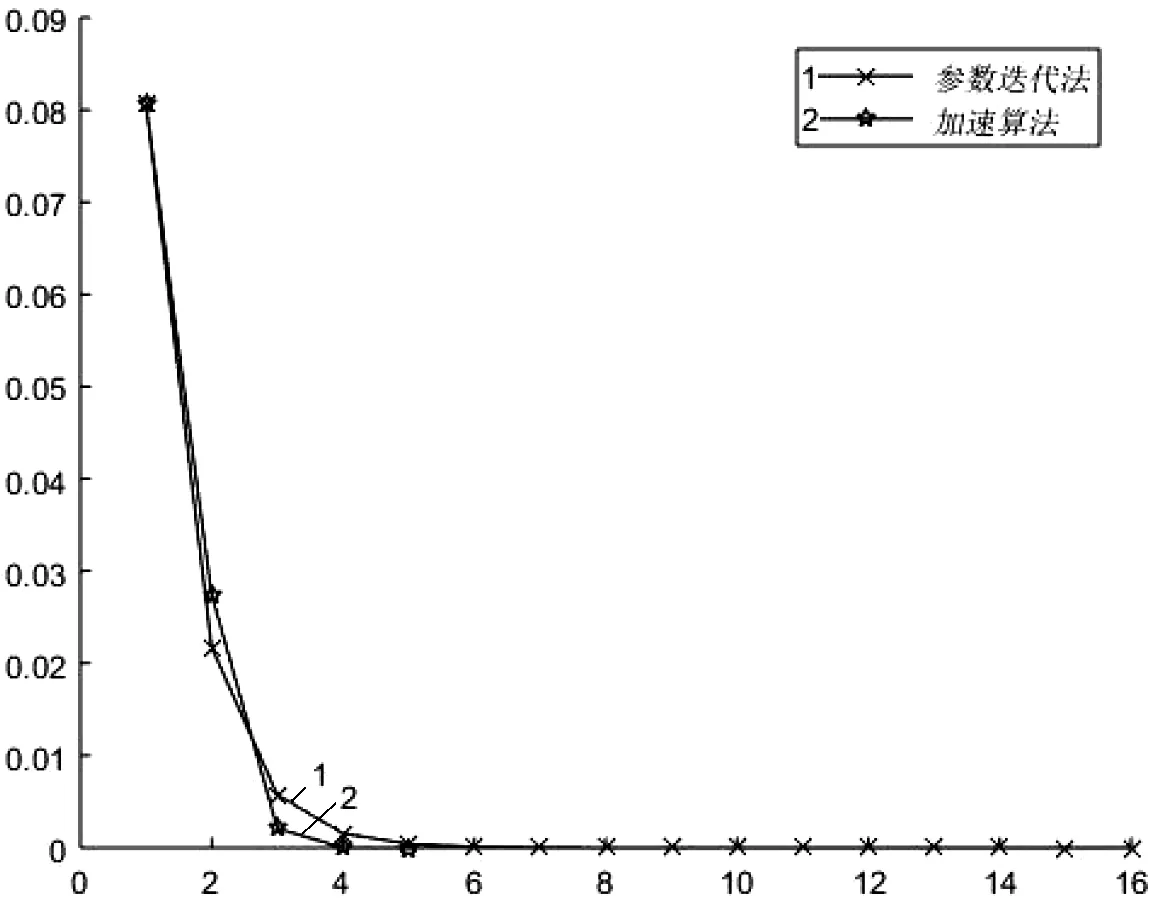
图2 例1中的迭代次数与误差(αaopt=-0.6387)Fig.2 The iterations and errors for Case 1

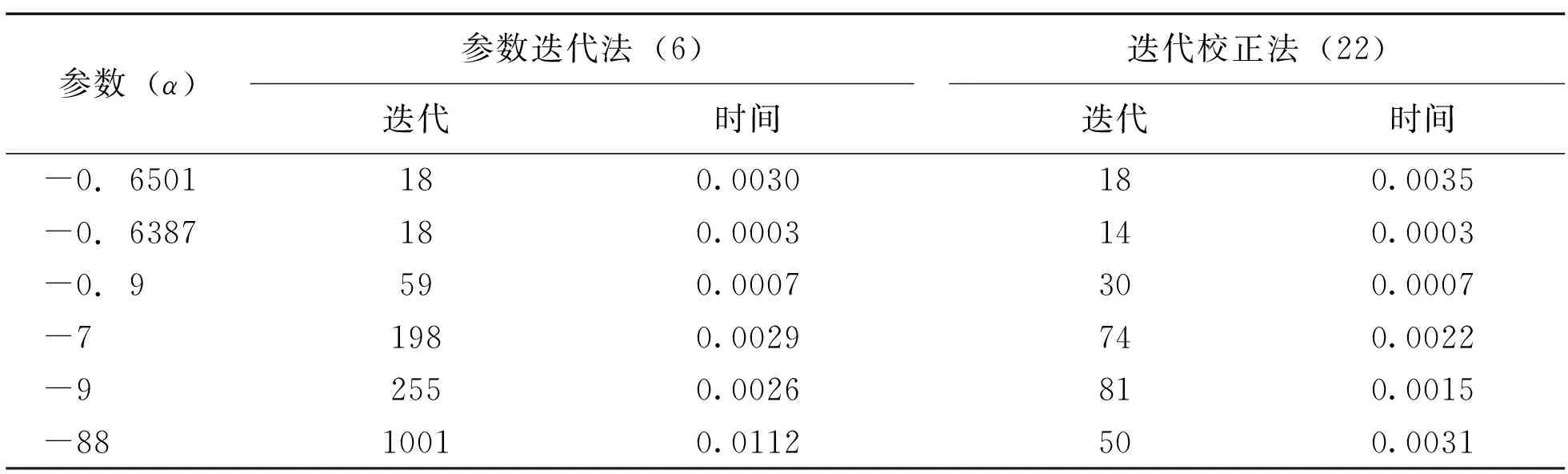
表1 不同α对于例1的数值结果

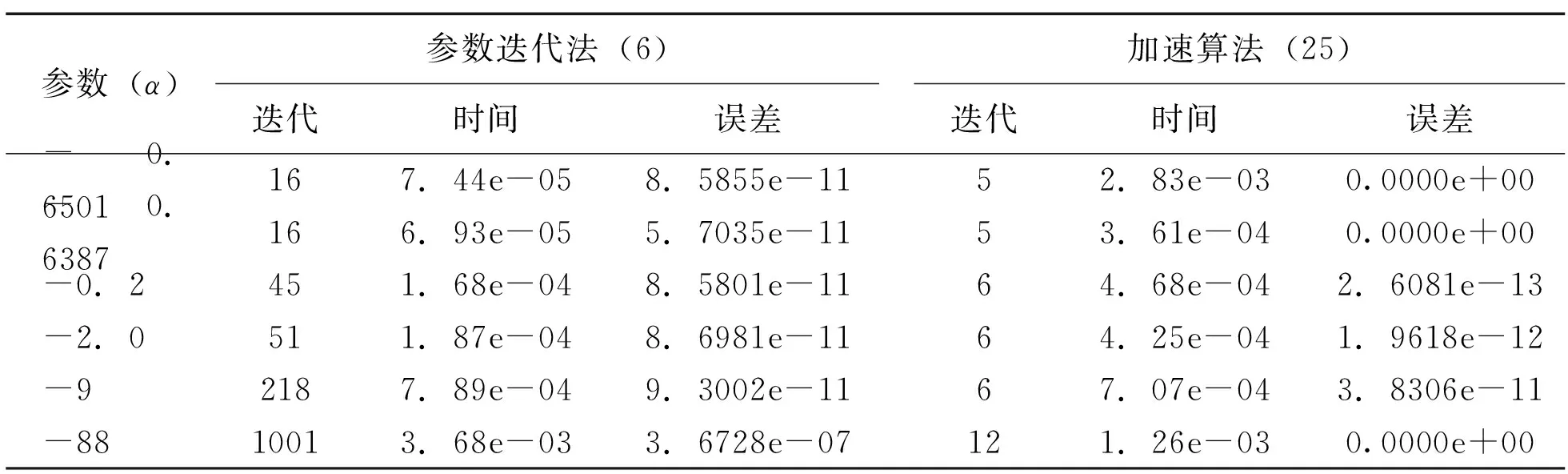
表2 不同α对于例1的数值结果

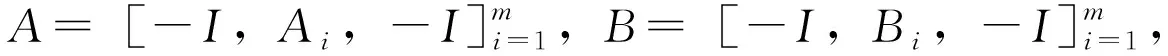
其中

通过计算得到矩阵方程AXBT+BXAT=I的解(m=100)。其中停止准则为‖xk+1-xk‖≤10-10令初始矩阵X0=Y0,对α取不同的值,则数值结果如下。根据定理4,求得αopt=-1.9916和αaopt=-1.8614。从图3和图4可以看出参数迭代法使用最优参数(αopt=-1.9916)和近似最优参数(αaopt=-1.8614)与加速算法的比较。同时,可以从表3 和表4看到参数迭代法(6)分别与迭代校正法(22)加速算法(25)的比较。数值结果见表3和表4。

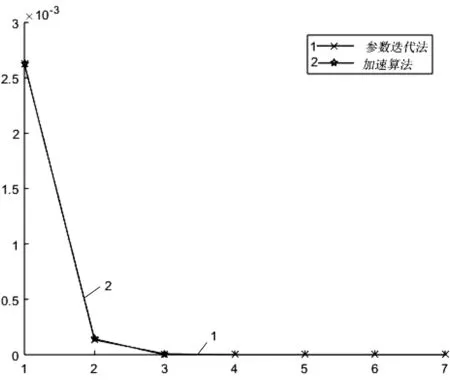
图3 例2中的迭代次数与误差(αopt=-1.9916)Fig.3 The iterations and errors for Case 2

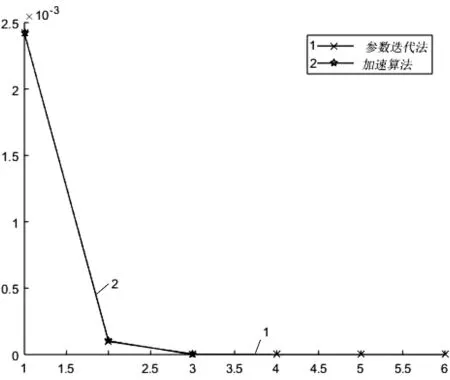
图4 例2中的迭代次数与误差(αaopt=-1.8614)Fig.4 The iterations and errors for Case 2

表3 不同α对于例2的数值结果

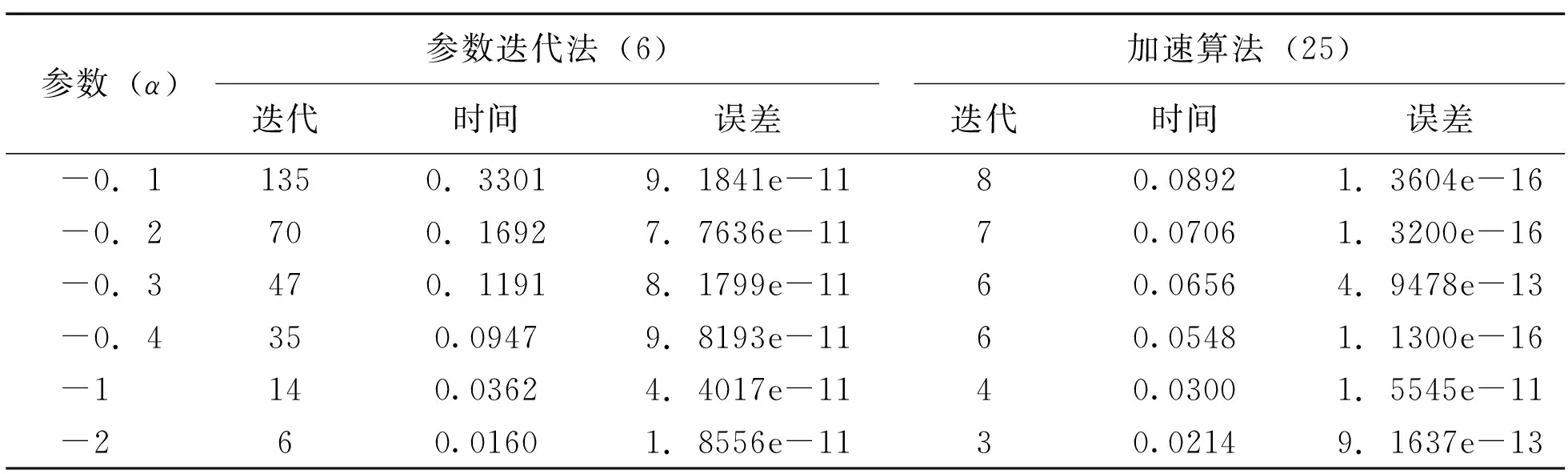
表4 不同α对于例2的数值结果

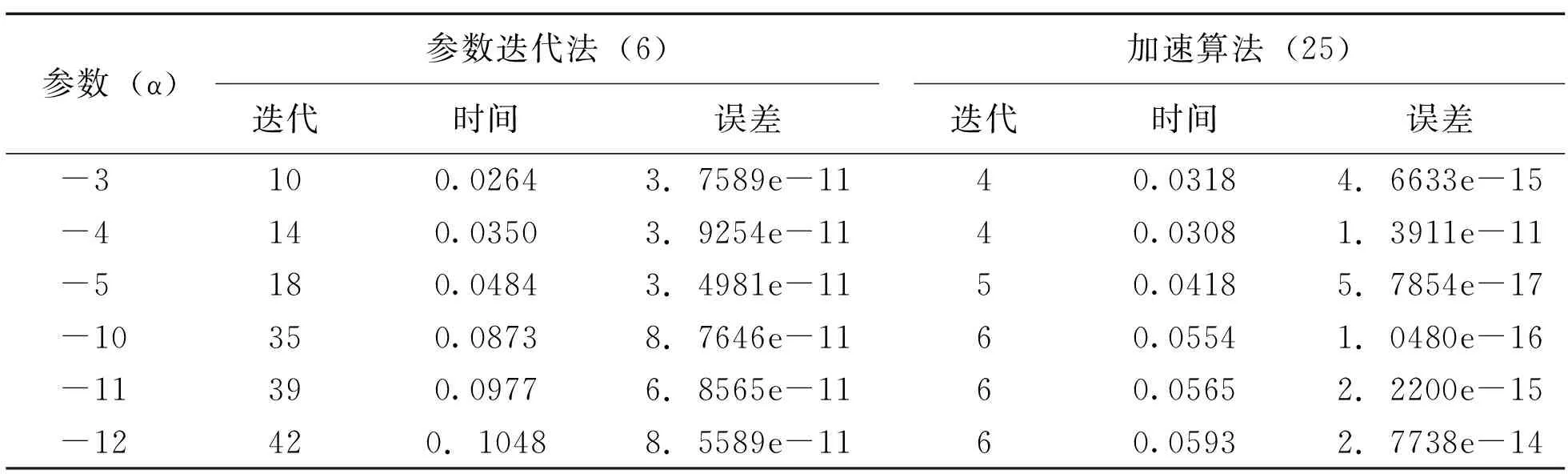
续表