Shallow-water sloshing motions in rectangular tank in general motions based on Boussinesq-type equations *
Yan Su (苏焱), Zu-yuan Liu (刘祖源), Zhi-liang Gao (高志亮)
1. Key Laboratory of High Performance Ship Technology,Ministry of Education, Wuhan University of Technology,Wuhan 430063, China
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China
Abstract: Based on the highly accurate Boussinesq-type equations in terms of velocity potential, the shallow-water sloshing in a two-dimensional rectangular tank is studied.The rectangular tank in harmonic sway, heave and roll motions with small excitation amplitudes is considered.The total velocity potential is divided into two parts: the particular solution and the remaining part to be determined by the Boussinesq-type equations.The Stokes-Joukowski potential is adopted in the particular solution for the roll excitation motion.The comparisons of the numerical results indicate that the shallow-water sloshing motions in a rectangular tank can be predicted well based on the Boussinesq-type equations.
Key words: Sloshing, shallow-water, Boussinesq-type equations
The sloshing phenomena were investigated with various approaches, e.g., the volume of fluid method,the boundary element method and the smoothed particle hydrodynamics (SPH) method.Reference [1]is a good review of the almost every aspect of the liquid sloshing dynamics.The regimes of sloshing motions vary due to different filling levels in the container.According to Ref.[2], the regimes of the fluid motion can be roughly divided into that based on the shallow water theory (h|l< 0.1), that with an intermediate water depth (0.1 ≤h|l≤ 0 .2-0.25) and that under finite water depth conditions (0.2-0.25<h|l< 1.0).Herelis the length of the tank andhis the filling level.For shallow-water waves, the Boussinesq-type equations are effective for predicting the behavior of the nonlinear waves[3-5].The original Boussinesq-type equations in terms of velocity were adopted for simulating the sloshing motions[6-7].In Ref.[7], the shallow-water sloshing motions in a rectangular tank were studied in sway, heave and roll motions with small excitation amplitudes.A modal decomposition of the spatial field for the Boussinesq-type equations was used and the results were compared with those obtained with a SPH scheme.With the motivations of improving the computational efficiency to have a more straightforward matching with the potential flow solvers, the Boussinesq-type equations were recast in terms of velocity potential in Ref.[8].
An advanced version of the model was given in Ref.[9]with some errors in Ref.[8]corrected.In Ref.[9], a new shoaling enhancement operator was used for ensuring that the definition of the vertical distribution of the velocity is always consistent with the kinematic bottom boundary condition, which is not the case for the Boussinesq-type equations in terms of velocity.
The highly accurate Boussinesq-type equations in terms of velocity potential were firstly adopted for dealing with the sloshing phenomena in Refs.[10-11].Different filling levels of liquid in a rectangular tank in only sway motion with small excitation amplitudes were discussed.In this paper, the sloshing motions in the rectangular tank in sway, roll and general motions are calculated and the numerical results are compared with the results in Ref.[7].For the sloshing motion in the tank in the roll motion, the Stokes-Joukowski potential is adopted for the particular solution.

Fig.1 The sketch of 2-D rectangular tank
A 2-D rectangular tank of lengthland filling levelhis adopted here (Fig.1).The origin of the tank-fixed Cartesian coordinate systemoyzis located on the middle of the free surface at rest.The direction ofz-axis points vertically upwards.For an inviscid, incompressible and irrotational flow, a vertical potentialΦ(y,z,t) exists in the fluid domain.
According to Ref.[9], the velocity potentialΦcan be found from the following boundary value problem.
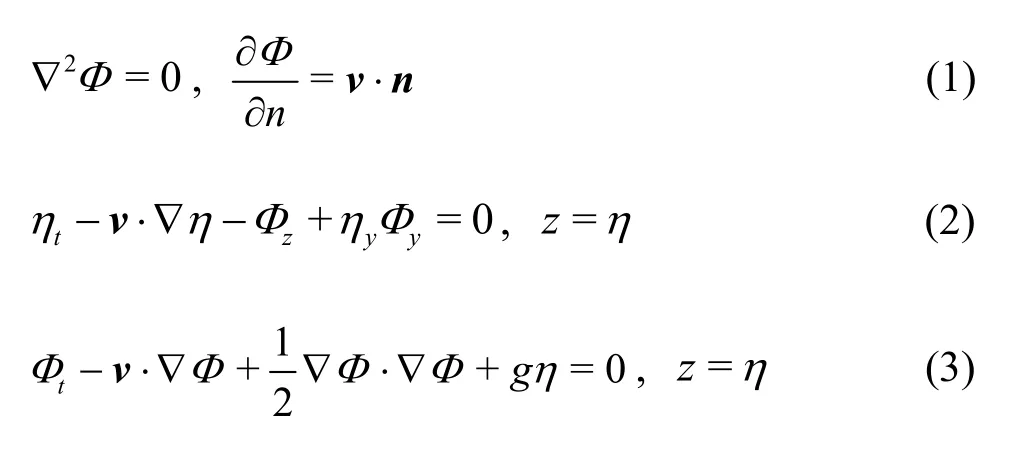
wherendenotes the outward normal vector of the tank walls andηexpresses the free surface elevation.gis the acceleration of gravity.
The total velocity potentialΦis separated into two parts:Φ=φ+φ.Hereφsatisfies the zero Neumann condition on the bottom and vertical walls and the Laplace equation in the fluid domain.The velocity potentialφcan be solved by the highly accurate Boussinesq-type model in terms of velocity potential.φis the particular solution of the boundary value problem.For the sway and heave motions,the particular solution is simple and can be given as follows

According to Ref.[2], the Stokes-Joukowski potentialΩshould be found for the roll motions.The boundary value problem for the potentialΩis expressed as follows:

The solution of the potentialΩcan be expressed as

where

With the particular solution for the sway and heave motions, the boundary value problem of the particular solutionφcan be obtained.
Following Ref.[9], the free surface conditions can be written in terms of the velocity potentialand the vertical velocitydefined directly on the free surface.The temporal derivatives of the free surface elevationηtand the velocity potentialΦ~tcan be given as follows:

The total velocity potential is divided into two parts: the particular solutionφis given before and the remaining part ofφcan be solved based on the Boussinesq approach.The details of the numerical method for the potentialφcan be found in Ref.[10].
With the solution of the potentialφand the particular solutionφ, the vertical velocityφzon the free surface can be obtained.The free surface elevation and the velocity potential in the tank are known initially.Based on the temporal derivativesandtη, the velocity potentialand the free surface elevationηin time can be obtained with the solution of the vertical velocity.
According to Ref.[10], a damping term due to the laminar friction on the walls is constructed for the Boussinesq-type model based on the linear theory.The linear damping term of the first sloshing mode is added to the right-hand side of the dynamic free surface condition

The damping coefficientB11is obtained by assuming a linear friction force on the wall, following, for instance, the Stokesʼ theory for the oscillation flat plate[12].
Based on the Boussinesq-type model, the sloshing motions in the rectangular tank in the sway,roll and general motions are calculated.The numerical results are compared with the results presented in Ref.
[7]where, the Boussinesq-type equations in terms of velocity were used and a modal decomposition of the spatial field was adopted to treat the exciting forces and the general motions.A rectangular tank in the sway, roll and general motions is discussed for shallow-water sloshing.The length of the tank is 1.175 m and the filling level is 0.060 m.The width of the tank is 0.120 m and the kinematic viscosity is.According to the linear dispersion relative, the first resonant frequency is

Fig.2 The com par isons of relative free surface elevations at the left wall at excitation frequency ω |ωr = 0.98 (a)and ω|ωr = 1.02 (b).The length of tank is 1.175 m and the filling level is 0.060 m
In Fig.2, the harmonic sway motion is considered with the excitation amplitude of 0.004 m.The free surface elevations at the left wall divided by the filling level give the values of the ordinates.The simulation takes long enough duration to ensure the attainment of the steady-state conditions.In Fig.2, the comparisons of the relative free surface elevations at excitation frequencies1.02 are shown.From the figures, the traveling waves with three-wave and two-wave regimes can be found in the tank at different excitation frequencies.Some small oscillations in the wave troughs can be found in the results of the Boussinesq type model.In fact, only the damping term of the first sloshing mode is adopted here, while 30 sloshing modes were used in Ref.[7].The small oscillations in the wave troughs appear reasonably.In general, the results obtained by using the Boussinesq-type model in terms of velocity potential agree well with the results given in Ref.[7].

Fig.3 The rela tive f ree surface elevations at 0.01l away from the left wall at different excitation frequencies ω |ωr :1.02(a),1.08(b),rollmotions.The length of tank is 1.175 m and the filling level is 0.060 m
The harmonic roll motion is shown in Fig.3.The maximum angle of the rotation is π/720.The excitation frequencies are1.08.The time histories of the free surface elevations at several different excitation frequencies are compared with those obtained by the modal system method.
From the comparisons in the figures, the results obtained by using the Boussinesq-type model are in an overall good agreement with the results in Ref.[7].The general motions (sway, heave and roll) of the rectangular tank are shown in Fig.4.According to the parameters in Ref.[7], the excitation amplitudes and frequencies are: 0.006 m and 2.20 s-1(for the sway motion), 0.030 m and 4.29 s-1(for the heave motion),/720rad π and 0.22 s-1(for the roll motion), respectively.The free surface elevations at the position of 0.01laway from the left wall divided by the filling level give the values of the ordinates.In Fig.4,the amplitudes of the free surface elevations calculated by the proposed model (b) are in an overall agreement with the results obtained by using the modal system method (a).The small oscillations in the wave trough can be found in the results of our Boussinesq model and the phase difference appears after long-time simulations.The damping term plays an important role in the small oscillations at high frequencies and the phase position.The damping term of only the first sloshing mode is not enough and the whole damping expression should be studied in the future.

Fig.4 The relative free surface elevations at 0.01laway from the left wall in tank in general motions.Results obtained by using modal system method (a) and Boussinesq-type model (b).The length of tank is 1.175 m and the filling level is 0.060 m
In conclusion, the shallow-water sloshing motions in the 2-D rectangular tank is simulated based on highly accurate Boussinesq-type equations in terms of velocity potential.The rectangular tank in sway,roll and general motions with small excitation amplitude is discussed.Compared with the results in the literature, the Boussinesq-type equations show a good performance, which means that the Stokes-Joukowski potential is suitable for the roll motion.The differences of the free surface elevations at high frequencies and the wave phase in a long time simulation are due to the damping term of only the first sloshing mode.
- 水动力学研究与进展 B辑的其它文章
- Call For Papers The 3rd International Symposium of Cavitation and Multiphase Flow
- A novel two-way method for dynamically coupling a hydrodynamic model with a discrete element model (DEM) *
- Air entrainment of hydraulic jump aeration basin *
- Fundamental diagrams for pedestrian flows in a channel via an extended social force model *
- Axial laminar velocity field calculation and optimization for power-law fluid in eccentric annulus with cutting bed *
- Numerical modeling of sediment transport based on unsteady and steady flows by incompressible smoothed particle hydrodynamics method *

