Numerical modeling of sediment transport based on unsteady and steady flows by incompressible smoothed particle hydrodynamics method ＊

Rasoul Memarzadeh , Gholamabbas Barani Mahnaz Ghaeini-Hessaroeyeh

1. Department of Civil Engineering, Faculty of Engineering, Shahid Bahonar University of Kerman, Kerman, Iran

2. Department of Civil Engineering, Faculty of Engineering, Vali-e-Asr University of Rafsanjan, Rasanjan, Iran

Abstract: The purpose of the present paper is to introduce a simple two-part multi-phase model for the sediment transport problems based on the incompressible smoothed particle hydrodynamics (ISPH) method.The proposed model simulates the movement of sediment particles in two parts.The sediment particles are classified into three categories, including the motionless particles, moving particles behave like a rigid body, and moving particles with a pseudo fluid behavior.The criterion for the classification of sediment particles is the Bingham rheological model.Verification of the present model is performed by simulation of the dam break waves on movable beds with different conditions and the bed scouring under steady flow condition.Comparison of the present model results, the experimental data and available numerical results show that it has good ability to simulate flow pattern and sediment transport.

Key words: Sediment transport, Bingham model, dam break, incompressible smoothed particle hydrodynamics (ISPH) method,steady and unsteady flows, two-part multi-phase model

Introduction

The sediment transport due to steady or unsteady flows is one of the important issues in the hydraulic engineering, which can cause immense damages.Therefore, modeling of sediment transport has been the subject of many studies for hydraulic engineers.With the promotion of computer technology and the numerical solution methods, one, 2-D and 3-D sediment transport models are extensively used for prediction of bed and suspended load transport with the unsteady and steady flows[1-5].

In the conventional sediment transport models,the governing equations of fluid and sediment phase are expressed in Eulerian form and common mesh based Eulerian methods such as finite difference and finite volume methods are used for discretization and solving these equations.Recently, the mesh-free Lagrangian particle methods have been used for numerical modeling of free surface flows.These methods can efficiently treat the large deformation of free surfaces and multi interfaces since there is no mesh distortion.SPH method is one of the most famous particle methods.It was originally developed for the astrophysical computations[6-7].Then, it has been extended to a wide range of fluid mechanics problems[8-16].In spite of SPH advancements, the majority of its applications in the field of free surface flows have been for single phase flows (e.g., dam break problem over fixed bed).

In the present paper, a two-part multi-phase ISPH model with sub-particle scale-large eddy simulation(SPS-LES) closure model is developed.In this model,based on the Bingham rheological model, a strength threshold is defined for each of the sediment particles.According to this threshold, the movement simulation of them is performed in two parts.When a sediment particle moves with a low velocity such that the shear stress of it does not exceed the defined threshold, only the shear stress term in the Navier-Stocks equations is considered to move it.Otherwise, the sediment particle is considered like the water particles, and all the force terms in the Navier-Stokes equations are used to simulate the movement of it.

This viewpoint for simulation of sediment particles is novel.In the previous studies, where the SPH method is used for the sediment transport, the study of Manenti et al.[17]uses the Mohr-Coulomb yielding criterion and Shields theory to describe the movement mechanism of the sediments.Manenti et al.[17]assume that the sediment particles to be fixed when the strength threshold is not exceeded.In other studies,Sibilla[18]developed a numerical model to study the local scour downstream of a protective apron caused by a planar jet flowing from a sluice gate based on the SPH description of the water flow which is coupled with a conventional description of the bed evolution based on the Exner equation.Furthermore, Ran et al.[19]developed a multi-phase SPH model for the bed load transport simulation which uses the concept of pick-up velocity to initiate the sediment grains.

To assess the multi-phase ISPH model performance, first the model is applied to the dam break problem on movable bed with different materials based on the experimental data of Spinewine and Zech[20].Then, the bed scouring downstream of an apron under steady-state flow conditions is studied based on the experimental data of Mohamed and Mccorquodale[21].Also, the convergence and accuracy of the Multi-phase ISPH model are investigated by alternating the particle resolutions and performing error analyses.

1.Numerical model

1.1 Governing equations

Considering the continuum description of sediment phase, the governing equations of multi-phase free surface flows are mass and momentum conservation equations which are expressed as:

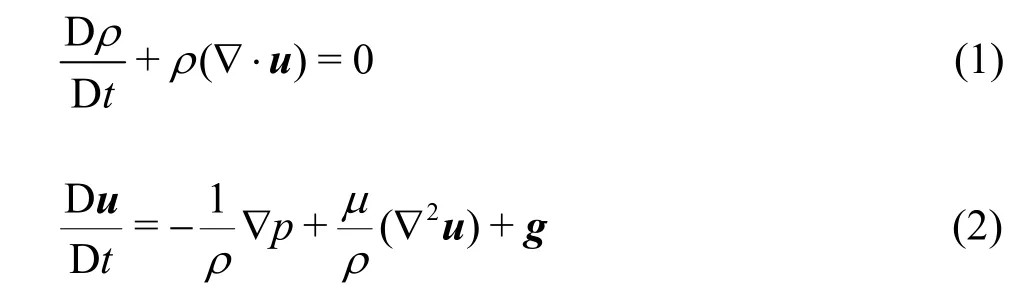
whereρ,u,p,μ,gandtare the flow density, flow velocity, pressure, dynamic viscosity, gravitational acceleration and time respectively.

To deal with turbulent flow conditions, a turbulence closure is required.In the present study, the sub-particle-scale (SPS) large eddy simulation (LES)model is implemented.In the LES approach, larger eddies are resolved and smaller or sub-particle-scale eddies are modeled.Using the flattop spatial filter on Eqs.(1), (2), the following Lagrangian particle scale equations are obtained[22]:

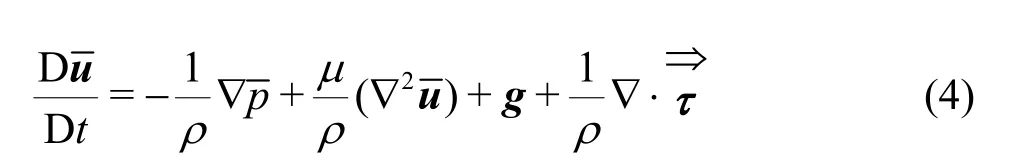
where “- ” denotes the particle scale components, andis the SPS stress tensor.SPS uses the same concept as the sub-grid-scale (SGS) LES model,which is used in Eulerian mesh-based systems.In the present study, the SPS fluctuations are modeled employing the Smagorinsky model[23].The SPS tensor term is described by the eddy-viscosity model[22]

wheretνis the kinematic eddy viscosityis the component of the strain tensor,kis the turbulence kinetic energy andijδis the Kroneckerʼs delta function.The eddy viscosity is modeled as follows

In whichCsis the Smagorinsky constant,dris particle spacing indicating the characteristic length scale of the small eddies andis second invariant of the filtered-field deformation tensor.In the following equations, symbol “- ” is dropped for convenience.

1.2 SPH theories and formulation

In this study, the standard SPH formulation is used for discretization of the governing equations[7].SPH method is based on a local weighted averaging of quantities and vectors.In SPH computation, the continuum domain is represented by a set of particles that are free to move based on the flow velocity.SPH formulation is obtained by interpolation between the particles (either in the same phases or different phases).The interpolation is based on the theory of integral interpolation, which uses the kernel function to approximate delta function.The kernel approximation offis expressed as

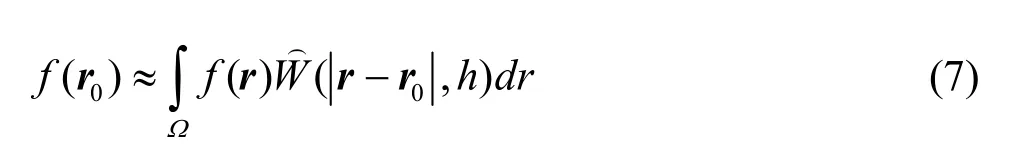
In the particle approximation, for any function of field variable, this formula is converted to

whereΩis the support domain,mjandjρare the mass and density of particlej,mj|ρjis the volume element associated with particlej,is the interpolation kernel function (in this paper kernel based on the spline function is used[7]),ris position vector,his smoothing distance andnis the total number of particles within the smoothing length that affects particlei.For example, the density of a particle in SPH approximation is represented as

The gradient and divergence operators need to be formulated in SPH algorithm if simulation of the Navier-Stokes equations is to be attempted.In this work, the following forms are employed for the gradient of a scalarAand divergence of a vectorB[24]:

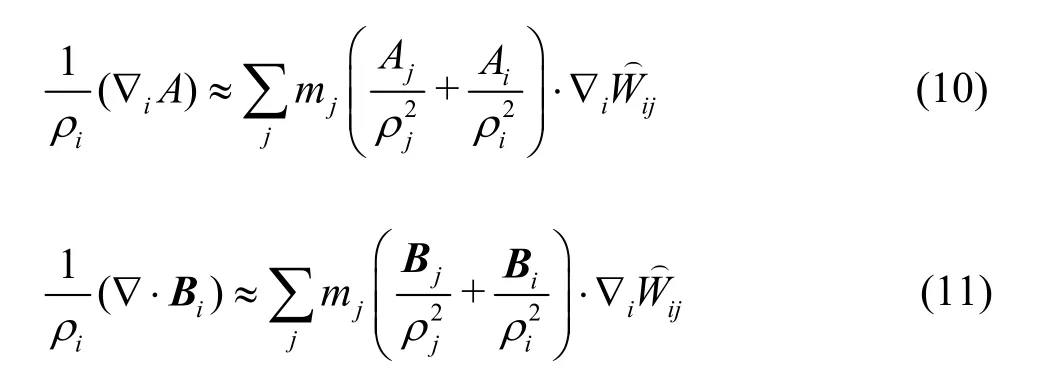
The pressure gradient in the SPH approximation is represented as

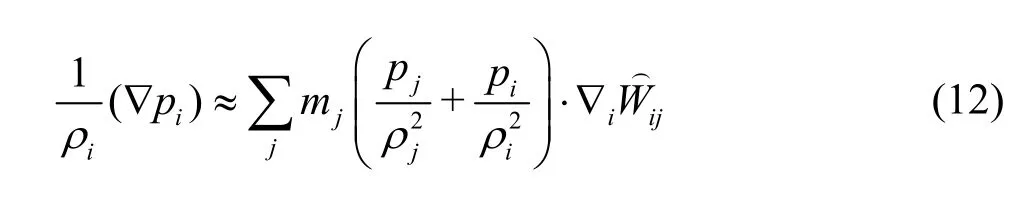
The Laplacian of the pressure and viscosity terms are formulated as the hybrid of a standard SPH which is coupled with a finite difference approximation.These are represented by the following equations[12]:

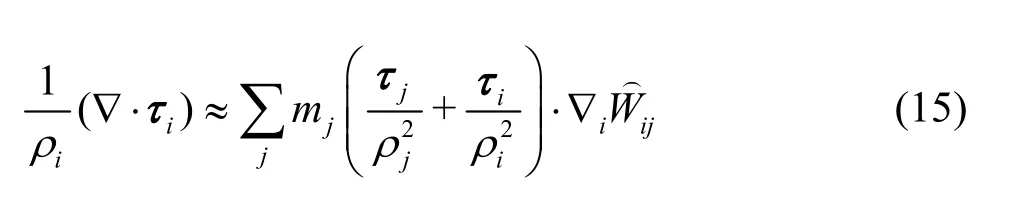
2.The two-part multi-phase model for sediment transport simulation

In the Bingham plastic model, material behaves as a solid layer when the shear stress is less than a yield stress,yτ, but it flows as a viscous fluid when stresses exceed this yield stress:

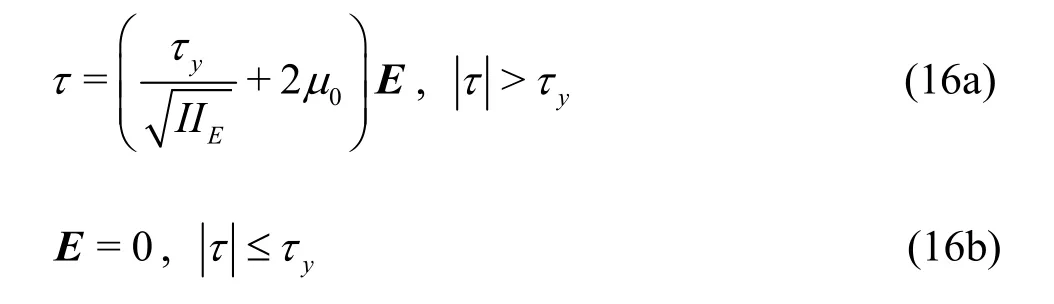
where0μis the flow consistency index depends on sediment mass density, sediment diameter and viscosity of the main fluid[25],Eis the rate of strain andis second principal invariant of the shear strain rate tensor[26].In the present model, the solid zone is approximated via a highly viscous fluid whose viscosity is much greater (say,α=200) than the flow consistency index (μ0).

For a Newtonian fluid, the following simple equation describes the relation between the shear stress and strain rate tensors

According to the Eqs.(16), (17), the following relations are used to represent the behavior of sediment phase:

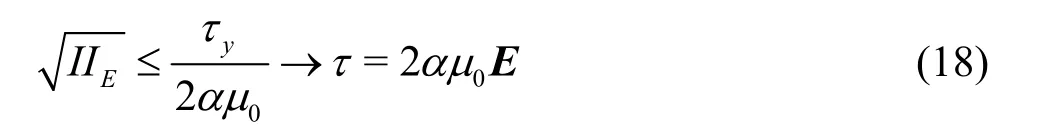
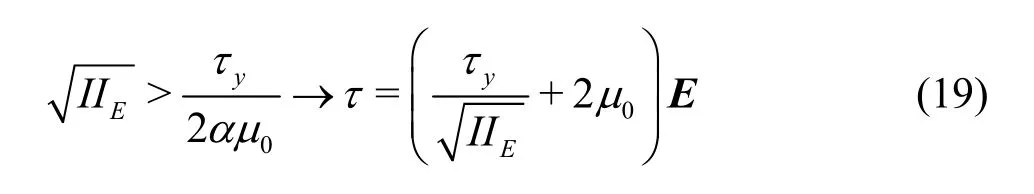
Therefore, the effective viscosity,μeff, for stresses higher than the yield stress is defined asotherwise, it is equal toα0μ.In the present study, the following relation presented by Kanatani[27]is used for the calculation of yield stress of bed sediment particles

wherecis the cohesion coefficient of sediment,φis the internal friction angle of sediment andis the normal stress between the sediment grains which in case of saturated sediment is buoyant pressure.

Furthermore, the multi-phase forces between different phases are calculated automatically.In the present multi-phase model, based on the properties of SPH method, the domain of the problem represents as particles with various density and viscosity.The behavior of a particle, which interacting with other particles in its neighborhood, depends on its viscosity and density and viscosity and density of neighboring particles.In the interface layer between sediment and water phase, particles of the same and another phase are used to discretize the equations of each phase particles.Thus, effect of difference phases automatically is applied to calculate the multi-phase forces for simulation of sediment (in both parts) and water phases.The consideration of density and viscosity differences in calculation multi-phase forces can be seen in Eqs.(12)-(15).As a result, the solution of separate equations for each phase and then calculations of the multi-phase are not required.Using this approach, difficulties in calculation of multi-phase forces are removed.

I have a step- mother who has bewitched me so that I am a white bear by day and a man by night; but now all is at an end between you and me, and I must leave you, and go to her

3.Solution algorithm

Suggested two-part multi-phase ISPH model,which is proposed to advance the solution in time, can be summarized in a simple algorithm, which consists of five steps:

(1) In the first step, second principal invariant of the tensor of shear strain rate of sediment particles is calculated, and Eqs.(18), (19) are controlled.Finally,in this stage, the type of behavior of sediment particles is defined, and the viscosities of these particles are defined.

(2) In the second step, for the water particles, the gravity and viscosity terms in Eq.(4) are considered to calculate temporary positions and velocities (u*and.In the case of sediment particles, according to Bingham rheological model, if the sediment particles behave like a rigid body, impermanent positions and velocities of them are calculated based on the shear stress terms in Eq.(4).Otherwise, the gravity and shear stress terms are used like the water particles.

(3) In the third step, the pressures of particles are obtained from the mass conservation (Eq.(1)), which is used to enforce incompressibility in the calculations.

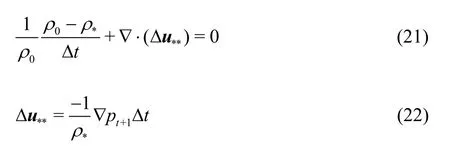
In these equations, Δu**is the velocity correction,is the initial density of particles,is the temporary density of particles.A Poisson equation is obtained by combining Eqs.(21), (22).Furthermore,the Eq.(23) yields the pressure of the particles as follows

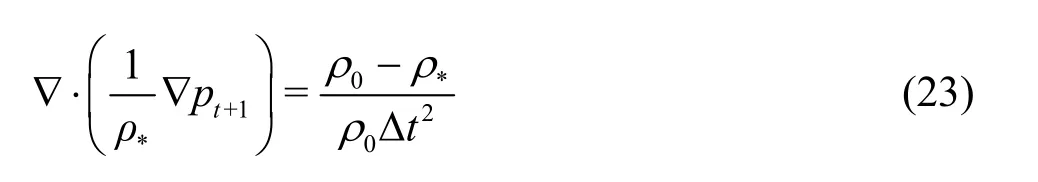
After employing the relevant SPH formulation for the Laplacian operator, a system of linear equations is obtained, and this system is solved efficiently by iterative solvers.

(4) In the fourth step, new velocities of water particles and sediment particles with pseudo fluid behavior are computed by the Eqs.(22), (24).For the sediment particles with rigid behavior, the pressure gradient term (Eq.(22)) is not applied.

(5) Finally, in the fifth step, the new positions of particles are obtained by the Eq.(25).

In the present model, the stability of the computations requires the following Courant condition

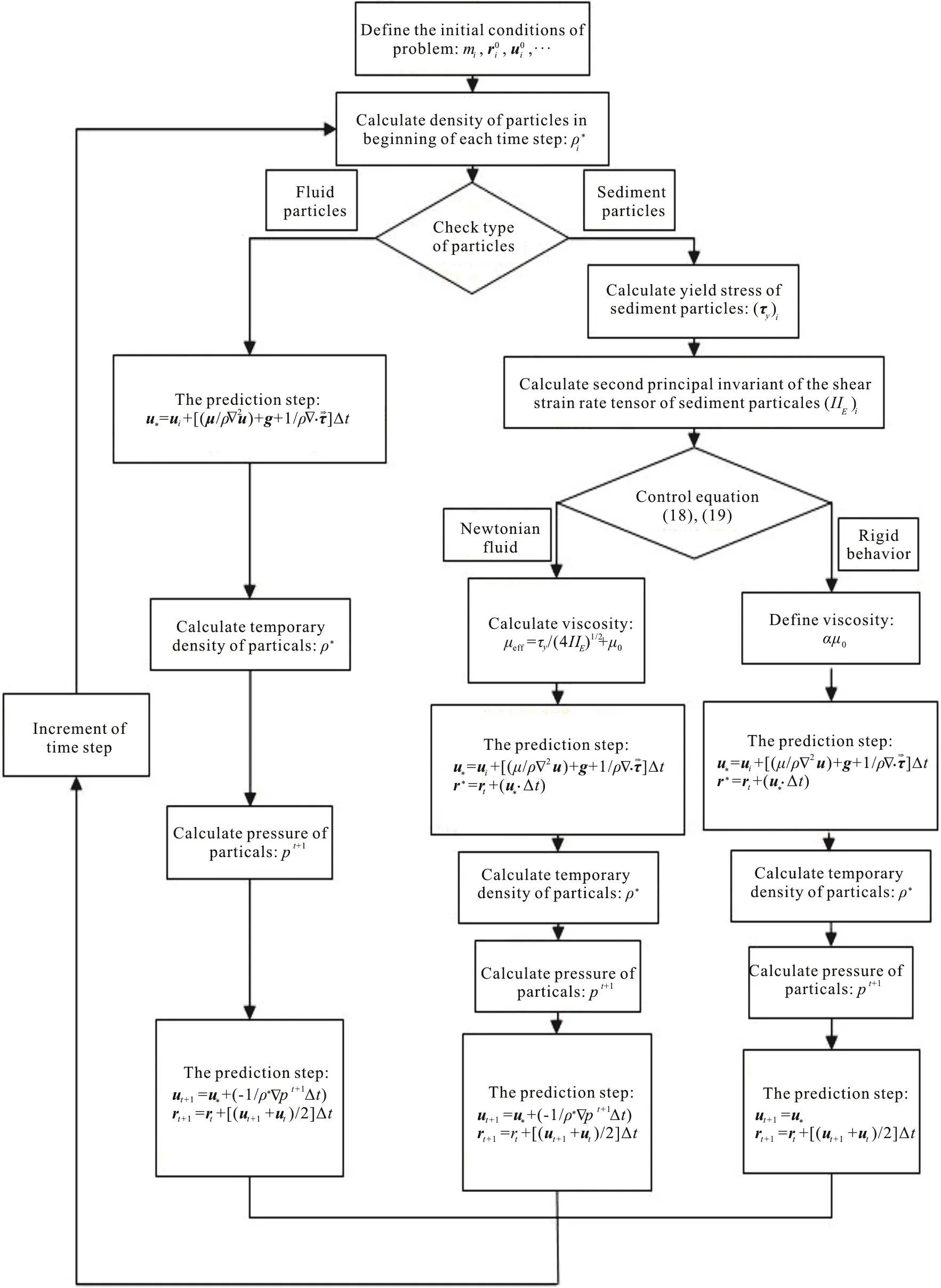
Fig.1 Algorithm of new two-part ISPH multi-phase model

whereumaxis maximum particle velocity in the computation domain.The factor 0.1 ensures that the particle moves only a small fraction of the particle spacing per time step[28].The flowchart of the proposed solution algorithm is shown in Fig.1.

4.Boundary conditions

Fig.2 (Color online) Initial geometry of dam break problem with movable bed (blue particles- water, brown particles-sediment)

In the present model, the free surface is automatically tracked.When the temporary density of particles() becomes smaller than 0.90-0.99 the initial density of them (), they are considered as a free surface particle.The solid boundaries are described by one line of fixed particles.Also, two layers of ghost particles are placed outside the boundary[28].Inflow and outflow are modeled by motion of particles toward and outward of the solution domain based on the recycling strategy, which is represented by Shakibaeina and Jin[29].

5.Results and validation

The verification of new two-part multi-phase ISPH model is performed in two steps.For this purpose, two laboratory experiments, namely dam break waves on the movable bed with different initial bed shapes and materials, which is a sediment transport problem under unsteady state flow, and bed scouring under a steady flow are used to validate the present model which is utilized to model the sediment transport problems.

5.1 Dam break over movable bed (Experiments of Spinewine and Zech[20])

In this section, the two-part multi-phase ISPH model is used for simulating the dam break waves over a movable bed with different conditions.The laboratory tests of Spinewine and Zech[20]are used to evaluate the accuracy of computations.

The geometry of the experiments consists of a horizontal bed with non-cohesive sediments, which are saturated with water and extending on both sides of the idealized dam.The dam is represented by the gate which is removed rapidly by lowering it (Fig.2).On the upstream side of the gate, an additional layer of pure water is at rest with constant depth (h0)[20].In this study, the flat bed with the same sediment level on both sides of the dam is considered for evaluation of the present model ().Two series of tests are performed in this section with two types of bed materials:

(1) Light cylindrical PVC pellets, with an equivalent diameter of 3.9 mm.

(2) Uniform coarse sand, with a median diameter of 1.82 mm.

The specific and bulk densities of PVC are 1 580 kg/m3, 1 336 kg/m3and the specific and bulk densities of sand are 2 683 kg/m3, 1 892 kg/m3.The bulk density is applied in the modeling.The angle of fraction for PVC and sand is 38°, 30°, respectively.It has been assumed that the gate is removed instantly.Depending on the size of the particles, each solid phase particle is representative of a certain number of solid phase grains, and its rheological behavior is defined based on the properties of the grains.

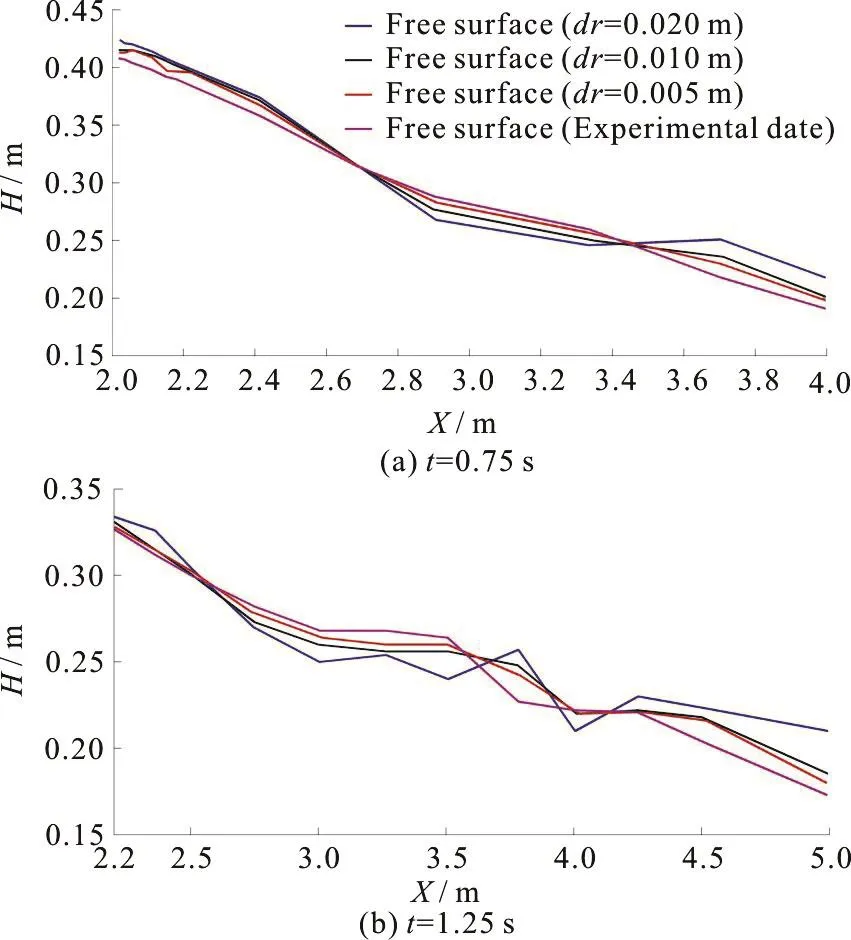
Fig.3 (Color online) Comparison of the present model results with different initial particle spacing with the experimental data of Spinewine and Zech[20]

Table1 The approximate average error between the present model results with different initial particle spacing and the experimental data of Spinewine and Zech[20]

5.1.1 PVC test with a flat sediment bed

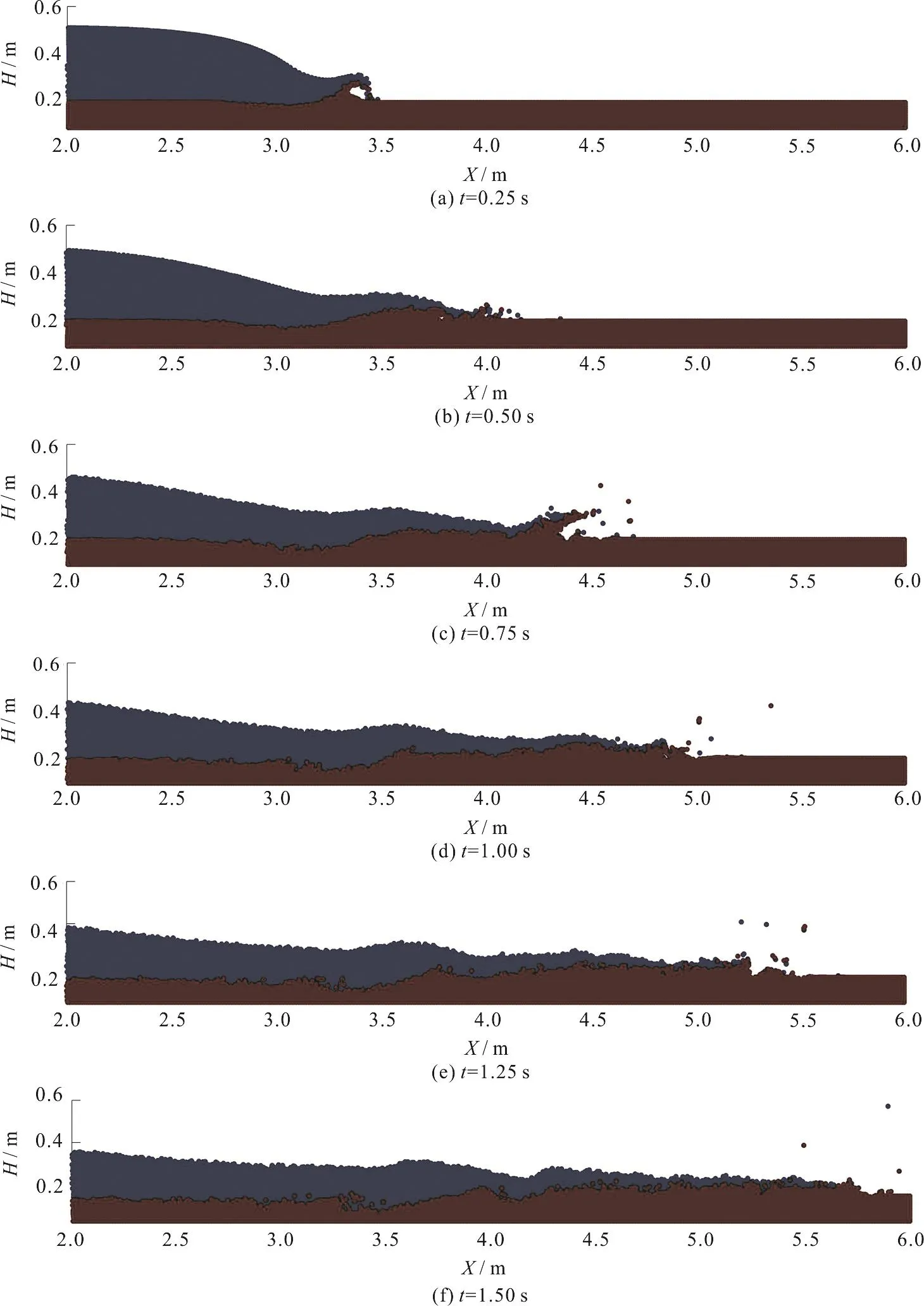
Fig.4 (Color online) Configurations of particles in different times after dam removal which are computed by new two-part multiphase ISPH model (blue particles-water, brown particles-sediment)

The experimental configuration which is chosen for this validation is PVC flat-bed that includes a water layer of depth 0.350 m in the reservoir and a fully saturated bed with a thickness of 0.125 m.In the first step, the model convergence study is performed to select appropriate particle spacing.The computations are made using three different particle spacings ofThese runs correspond to the particle number of 5 589,20 163 and 76 311, respectively.In Fig.3, the quantified comparison of the model results with different particle resolution and experimental data of Spinewine and Zech[20]is presented at selected timet=0.75 s,1.25 s after the dam break.Furthermore, an approximate calculated error between the results of new twopart multi-phase model and experimental data is shown in Table1.The comparisons have demonstrated that the differences between the numerical results and experimental data consistently decrease when the particle sizes become smaller.In addition, the numerical differences between the two finer computations are smaller than those between the two coarser computations.Because the time of computations withdr= 0.005 m are very larger than that of withdr= 0.010 m , and the results withdr= 0.010 mhas a reasonable agreement with theexperimentaldata,thedr= 0.010 m is selected as optimal particle spacing.

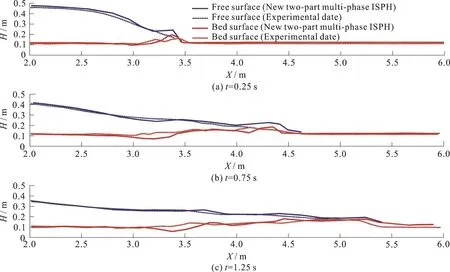
Fig.5 (Color online) Comparison between the result of free and bed surface of the new two-part multi-phase ISPH model and the experiments of Spinewine and Zech[20]

Fig.6 (Color online) Comparison between the result of free and bed surface of the new two-part multi-phase ISPH model and multi-phase MPS method of Shakibaeinia and Jin[30]

In Fig.4, the computational particle configurations at different times (t=0.25s-1.50s)after gate removal are shown.It is obvious from the Fig.4 that the water wave immediately propagates on the downstream bed, and the bed erosion is caused after removing the gate very fast.At the later stages of the dam break flow as the flow velocity deceased, the development of the erosion also decreased gradually,and the scour hole tends to be flat along the downstream direction.Furthermore, it can be seen in the model results that near the wave front, the displaced sediments almost cover the flow depth, such as what is observed in the experiment.Near the extremity, bulking of the sediment material into the flow is so intense that it saturated the full flow depth,forming a debris-flow like wave front.

It is clearly shown in the Fig.4 that the suspension process of sediment particles in the water layer is simulated well.In the initial steps of propagation of dam break wave over the movable bed, because the velocities of water particles are larger than that of the bed particles, the scouring process is performed, and some of the bed particles are suspended in the water layer and move along the downstream of the flume.In the later steps, according to the velocity of sediment particles, some of them are deposited and then resuspended in the water layer.Furthermore, the trapping of water particles within the bed load particles are considered (t=0.75 s, 1.00 s in Fig.4).In the present model, when the velocities of water particles became smaller than the bed load particles, these particles are trapped in the sediment phase.Due to the Lagrangian nature of the model, this process also automatically simulated, which is an advantage of it.

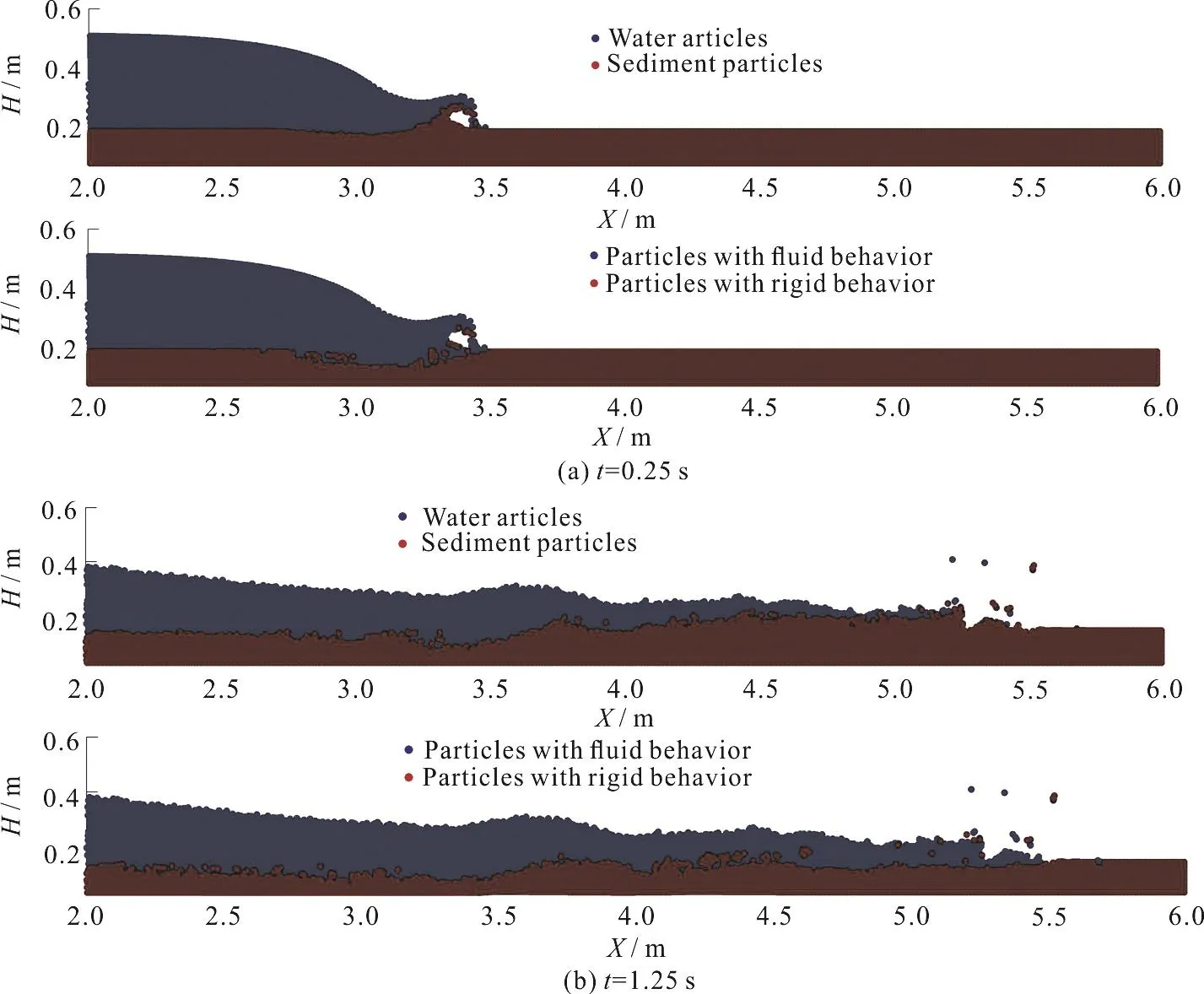
Fig.7 (Color online) Configurations of the water and sediment particles in t=0.25 s, 1.25 s after dam removal (The hrizontal and vertical units are meters)

Fig.8 (Color online)The new two-part multi-phase ISPH model results for the velocity field of the PVC test with a flat sediment bed at t=0.25 s, 0.75 s and 1.25 s

Furthermore, In the Figs.5, 6, an approximate quantified comparison of the results of the new twopart multi-phase ISPH model and the observations of Spinewine and Zech[20]and results of Shakibaeinia and Jin[30]are presented, respectively.The comparison between the model results and the experimental data for the water and bed surface and the position of leading edge shows the ability of the developed model for simulation of dam break wave over a movable bed.Moreover, the satisfactory agreement between the model results of bed surfaces with the experimental data shows that the new multi-phase model successfully reproduces the behavior of the sediment phase.In addition, according to the comparison of the results,there are some discrepancies between the experimental data and model results.They may be due to the mechanism of the gate removal and the dimensions of the experiment (3-D) which has some effects on the mechanism of the sediment erosion and deposition,while the current simulation is based on the 2-D vertical model.These discrepancies in the bed scouring profile are observed in other models such as Zech et al.[31], Shakibaeinia and Jin[30]and Ran et al.[19].They have noted the same reasons for the differences between the numerical results and the experimental observations.Also, there is a satisfactory agreement between the present model results and results of Shakibaeinia and Jin[30]which used MPS multi-phase model to study dam break flow over the mobile bed.It used the two-part multi-phase model for sediment transport simulation with different governing equations in each part of the present model, while the model of Shakibaeinia and Jin[30]is based on MPS method, which used a single set of equations to model the dam breaks over the movable beds with a rheological model to calculate the viscosity of sediment phase.

As mentioned in the previous sections, the new two-part multi-phase ISPH sediment transport model has two parts.In this model, in the first steps of simulation, most of the bed sediment particles have a solid behavior which is shown in the Fig.7.In these times, the particles move like a rigid body under the influence of water flow velocity.Furthermore, as shown in Fig.8, the velocity in the water region is much larger than the velocity in the sediment area.With the passing of time after the dam break occurred,the drag effect of water particles on the bed particles causes that the velocities and stresses of interface particles are increased.When the stresses of sediment particles become larger than the yield stress, these particles behave like the fluid particles.The numbers of these particles are increased by passing the time,and the interface solid bed turns to debris flow that in the present model, this matter can be observed well.Also from the Fig.8, it is observed that the velocity has relatively smoothed profiles and noise free, even near the sediment–water interface.Furthermore, the erosion area, which is observed in Fig.4, is near the area with the maximum of velocity vectors.The velocity is continuous across the interface layer, and the velocities of water particles are larger than that of the bed particles.This matter is the main factor of bed load particlesʼ motion.

To further demonstrate the robustness of the new two-part multi-phase ISPH model, the computed longitudinal velocity, tangential stress and yield stress at selected vertical locations of the dam break flow are shown in Figs.9, 10, respectively.For the instantaneous velocity profile at timet=0.25 s, 0.75 s and 1.25 s, they are plotted at three vertical locations near the flow front.The present computations of the velocity profile are quite consistent with the experimental and numerical findings of Spinewine and Capart[32], in which the velocity variations in the water layer demonstrate an almost constant pattern while they decrease in a linear manner inside the movable bed load layer.Furthermore, the computed tangential and yield stress profile in the bed load layer at timet=0.25 s, 0.75 s and 1.25 s are shown in Fig.10.In the present model, the comparison between the two graphs is the index of motion of sediment particles.Where the shear stress is greater than the yield stress,the sediment particles flows as a Newtonian fluid, and all the force terms in the Navier-Stokes equations are considered for the movement of them.Furthermore, it is observed that the tangential stress distribution is increased linearly towards the water-sediment interface and decreases to zero near the immovable boundary.There is a shear stress jump inside the bed load layer and the maximum value is found somewhere below the interface.This is the area where the sediment particles are mostly influenced by the water flow drag.Although there is no reference data available for a comparison, the tendency of the tangential stress curve seems to be reasonable.

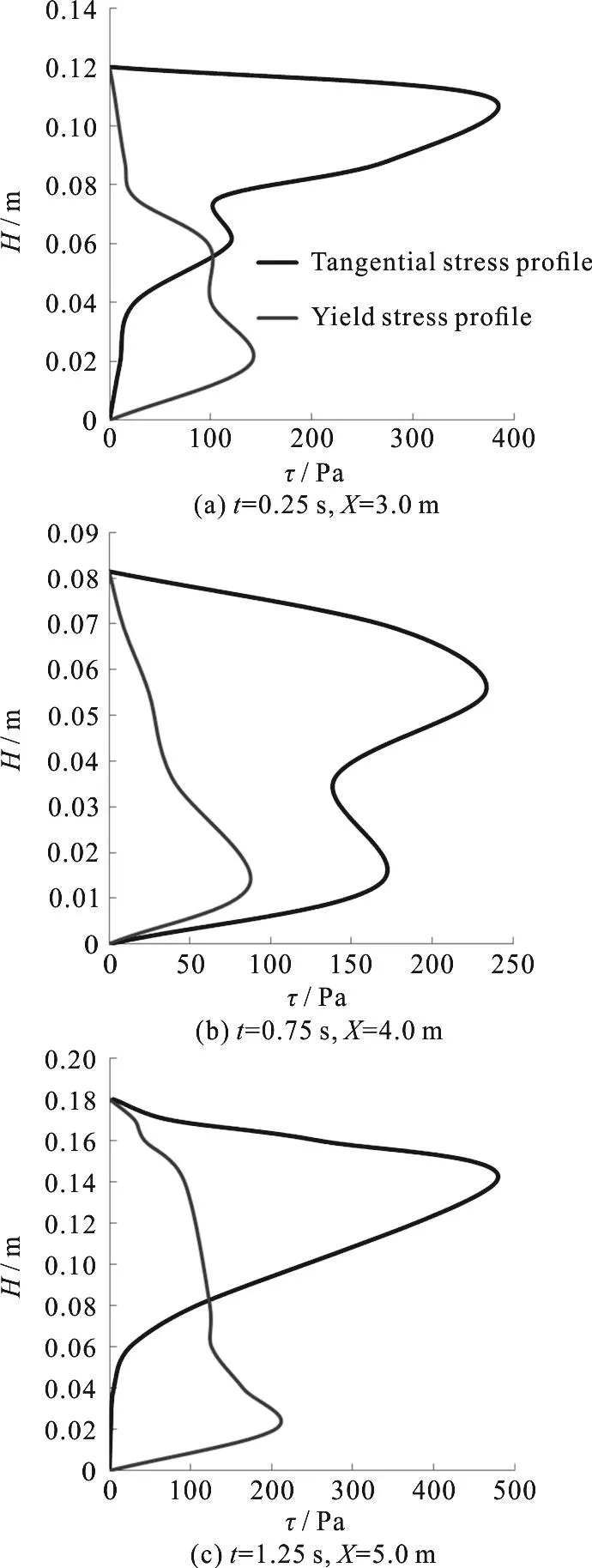
Fig.10 Instantaneous tangential and yield stress profiles at various locations at t=0.25 s, 0.75 s and 1.25 s

5.1.2 Sand test with a flat sediment bed

In the previous section, dam break problem with the granular bed made of PVC pellets are investigated.In this section, to validate the new two-part multiphase ISPH model for simulation of multi-phase flows with considerable differences between properties of two phases, propagation of the dam break wave on a horizontal sediment bed which is made of uniform coarse sand, based on experiments of Spinewine and Zech[20], is modeled.The initial geometry of this problem is exactly similar to PVC test with a flat sediment bed.The total number of particles in this problem is 20 163 particles (similar to PVC test).

It is shown in Fig.11, the particle configurations at different times (t=0.25s-1.00s)after gate removal.Compared with the PVC flat-bed results, some differences can be observed in the sand results,including:

(1) Since the density of sand is higher than PVC,the erosion in the sand bed is less, and the sediment transport layer is thinner than the PVC bed.

(2) The wave propagation in the sand bed is substantially faster.Consequently, the free surface elevations behind the front are shorter than the PVC bed.This may be due to the decreased fraction and less intense erosion.

In this test, the suspension process of bed particles in the water layer is modeled well.When the velocities of interface particles are larger than the pick-up velocity of these particles, they move with the water flow.

In Fig.12, this comparison between the results of the new two-part multi-phase ISPH model and the experimental data of Spinewine and Zech[20]are presented.In the Fig.12, it is observed that the entire propagation processes of dam break wave on the sand bed are well simulated by the present model, and it is obtained a relatively good agreement in the free surface and bed profile.The verification of the model with this test shows that the developed model has the capability for simulation of two-phase problems with large differences between the densities of two phases.

5.2 Bed scouring downstream of an apron (Experiment of Mohamed and Mccorquodale[21])

In two previous sections, two unsteady tests are used to validate the present model.In this section, the validation of new two-part multi-phase ISPH model is performed by simulating bed scouring under steadystate flow.A large number of sediment transport flows have steady conditions with an equilibrium or nonequilibrium state for the rate change of bed load.Examples of these flows are scouring around the bridges and downstream of a spillway.

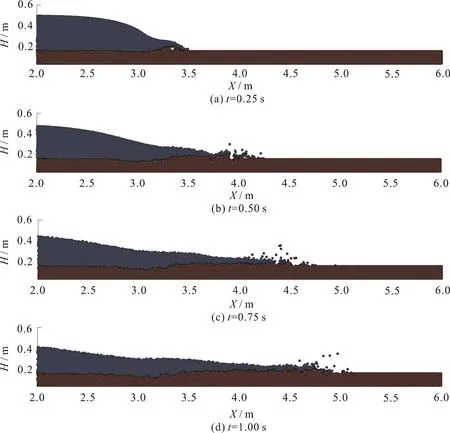
Fig.11 (Color online) Configurations of particles in different times after dam removal which are computed by new two-part multi-phase ISPH model (blue particles-water, red particles-sediment)

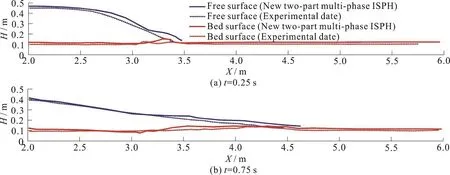
Fig.12 (Color online) Comparison of the free and bed surface results of the new two-part multi-phase ISPH model and experimental data of Spinewine and Zech[20]

The experiment of Mohamed and Mccorquodale[21]is used to evaluate the present model.We use experiment No.run 49 of Mohamed[33].A sketch of the initial configuration of this experiment is shown in Fig.13.In this experiment, a rectangular flume with a constant width of 0.42 m is used.The length of horizontal section reaching apron is 1.00 m, and in downstream of this apron, a bed layer of saturated marble chips with length 4.88 m and height 0.15 m is set.The specific gravity and median diameter of the bed material are 2.65 mm and 2.70 mm, respectively,and the angle of friction is 37°.It is considered that the sediment particles are saturated, therefore, the bulk density of particles equal to 2 000 kg/m3is applied in the computations.The water entered the apron with constant dischargeQ= 0.01578l/s and depthh0= 0.0218 m .The Froude number of water flow on the apron isFr= 3.68, so the flow is supercritical.The time of this experiment lastedt= 240 s ,which is applied in the computations.During the modeling, by using convergence analysis similar to the previous tests, a particle spacing ofdr=0.002 m is used.

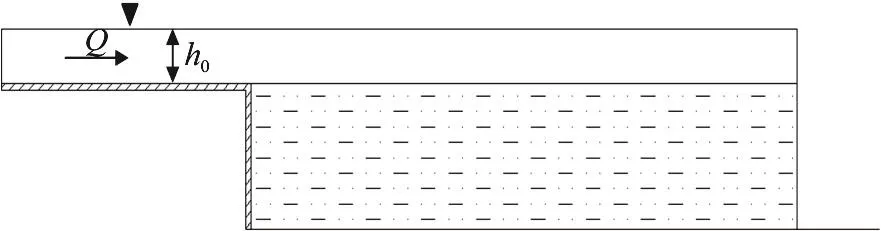
Fig.13 Definition sketch of bed scouring problem under steady flow

Fig.14 (Color online) Configurations of particles in different times after start of test, and comparisons between the bed profile result of the two-part multi-phase ISPH model and experiment of Mohamed and Mccorquodale[21] (blue particles-water,red particles-sediment, black line-experimental data)

In this test, two different regimes are observed,including the attached jet phase and the plunging jet phase.In the beginning of scouring process, the water flow is attached to the bed (t=30 s, 60 s in Fig.14).When the flow reaches the sediment bed, the shear stresses on interface particles are lower than the yield stress of bed particles.In the first regime, due to the high speed stream, the shear stresses in the interface layer are increased in a few seconds.Therefore, the behavior of bed particles is turned from the rigid to pseudo fluid, when severe bed load transport occurred.

In the first regime (untilt=60s), the bed erosion is done by two main factors, including the high shear stress and high pressure gradient.The ability of the present model, which divides the transport of bed particles in two parts, is used in this step.Before the bed particles behave like the pseudo fluid, only the shear stress term is used to simulate the movement of bed particles, and the bed erosion is performed with low speed.After these steps, when the interface bed particles show a fluid behavior, the pressure gradient term is also used to move them.Therefore, the erosion process is modeled with higher accuracy, which is very similar to the real situation.During the first regime, the rapid growth of the mound with a consequent rise in the effective tail water level is performed.At these times an explosive re-suspension of bed material is occurred.

Thereafter, in the next minutes, the second regime is formed (t= 240s in Fig.14).The attached jet from the apron plunges to the bottom of the scour hole and causes severe scour.Moreover, the energy dissipation regime is considered as well.It is the main factor of creating bed scouring in the second regime.

6.Conclusion

A two-part multi-phase ISPH model is developed to simulate the movement of sediment under unsteady and steady flows.SPH is a mesh-less particle based method, which has high ability to model flows with large deformations.The proposed model simulates the motion of sediment particles based on their behavior,and the Bingham-plastic model is used to present this behavior.In the present model, in the rigid phase of bed sediments, the movement of sediment particles is performed considering the forces caused by the shear stress.Otherwise, all the Navier-Stokes equationsʼ terms are used for simulating the movement of sediment particles.The incorporated LES based SPS turbulence model using the Smagorinsky eddy viscosity is utilized to investigate the effects of turbulence on the bed scouring.The results show that the two parts strategy for sediment particle movements is very appropriate for simulation of bed load transport under flows with high deformation.The free surface of flow and interface between different phases are modeled with satisfactory accuracy.The advantages of the presented two-part multi-phase model are its intuitive and easily implemented numerical scheme.In the dam break over the movable bed, scouring, deposition and re-suspension processes are considered well.In the bed scouring under the steady-state flow test, the two main regimes are found during the erosion.The attached jet phase and plunging jet phase are these two regimes.In the first regime, the number of particles which behave like the Newtonian fluid particles and depth of tail water are increased, and in the second regime, the severe bed erosion due to the energy dissipation factor is occurred.The alternative computations using three different particle spacing are performed to verify the convergence of the numerical scheme.Due to the successful application of the presented model for simulation of the bed scouring under flows with various conditions, it shows that the present model can be applied for simulation of sediment transport.