基于压缩感知与扩展小波树的自适应压缩成像

骆 乐， 陈 钱， 戴慧东， 顾国华， 何伟基

(南京理工大学 电子工程与光电技术学院， 江苏 南京 210094)

1 引 言

压缩感知理论[1-2]由于能够降低成像过程中对传感器的要求，通过对成像目标的全局少量的采样，代替传统的采样，在相同采样率的情况下，可获得更高的图像质量，已被越来越多地应用于光学成像的各个领域[3-4]。在图像重构过程中，图像的重构质量只与采样个数有关，个别采样值对重构图像质量的影响极小，所以即使在存在噪声污染的情况下，仍然可以较大概率恢复出目标图像，因此基于压缩感知理论的光学成像可在一定程度上减少噪声对成像质量的影响。然而由于成像压力从采样端转移到了图像恢复端，随着图像尺寸的增大，重构图像所需的时间呈现指数增长。如何降低压缩感知成像算法的复杂度，减少成像时间，通过新的压缩采样方式获得计算量小且质量更好的图像，是压缩感知理论更好运用于实践的关键所在。

为了解决上述问题，Deutsch、Averbuch和Dekel提出了基于小波树结构的自适应压缩采样方法[5-6]。2013年，Aßmann和Bayer将自适应压缩采样方法应用于鬼成像技术，提出了压缩自适应鬼成像方法(Compressive adaptive computational ghost imaging，CCGI)[7]。相比于压缩感知，这种方法所需采样次数更少，图像重构速度快，适合于任意尺度的图像恢复[8]。Dai等[9]提出基于扩展小波树的自适应成像方法(EWT-ACS)，Huo等[10-11]提出的系数指导下的单像素成像方法(Adaptive single-pixel imaging method based on guided coefficients，GC-ASPI)和基于共享机制与兄弟关系的压缩自适应鬼成像方法[12](Compressive adaptive ghost imagingviasharing mechanism and fellow relationship,SMFR-CAGI)，进一步挖掘小波树中各节点之间的关系，有效提高了对采样位置预测的准确性，提高了采样率和图像重构效果，减少了重构所需时间。然而基于扩展小波树结构的采样法，由于直接采样重要小波，采样过程中受噪声影响较大。除此以外，Yu等提出了自适应压缩鬼成像(Adaptive comprssed ghost imaging, ACGI)方法[13]，该方法结合了CS与CCGI的优点，进一步减少了测量次数，且抗噪性较好。但是ACGI在利用小波树确定采样区域的过程中，每次循环都需要运用CS重构算法计算小波系数，计算量大。

针对上述问题，本文在扩展小波树的框架下，结合CS理论给出了一种基于压缩感知与扩展小波树结构的自适应采样的压缩采样成像方法。将自适应成像中点对点采样获得目标的低分辨率的图像方法改为利用数字微镜阵列(Digital micro-mirror device,DMD)分区控制与CS重建，增强了信息获取的准确性，减少了采样次数。运用扩展小波树对采样位置进行预测，最后通过小波逆变换完成图像重构。

2 数字微镜阵列分区控制与小波树结构

由于单像素相机技术将传统的并行采样转换为串行采样，增加了采样时间，图像重构算法在恢复高分辨率图像时需要较长的运行时间。相比于高分辨率成像，这种技术更适用于低分辨图像的获取。基于小波树结构的压缩采样模型，在采用低分辨图像后，通过采样重要小波系数，再由小波逆变换即可获得所需图像。将两种采样方法结合可以用于实际中的压缩采样与成像。

2.1 基于单像素相机的DMD分区控制采样

DMD分区控制[10,14]是将原先的DMD中的每个微镜按区域划分后，使得相同区域的微镜在投影过程中按相同的状态进行翻转。该翻转过程由编程控制单个静态存储器(SRAM)单元的加载状态来实现。由压缩感知理论的测量矩阵的性质，采用二进制随机测量矩阵，SRAM的加载状态由矩阵中的各元素值决定。因此DMD分区控制本质上是将同一区域的多个微镜组成一个大的微镜，降低了原先DMD的分辨率，增强信息获取的准确性[15]。DMD分区控制的过程如图1，引自文献[14]。

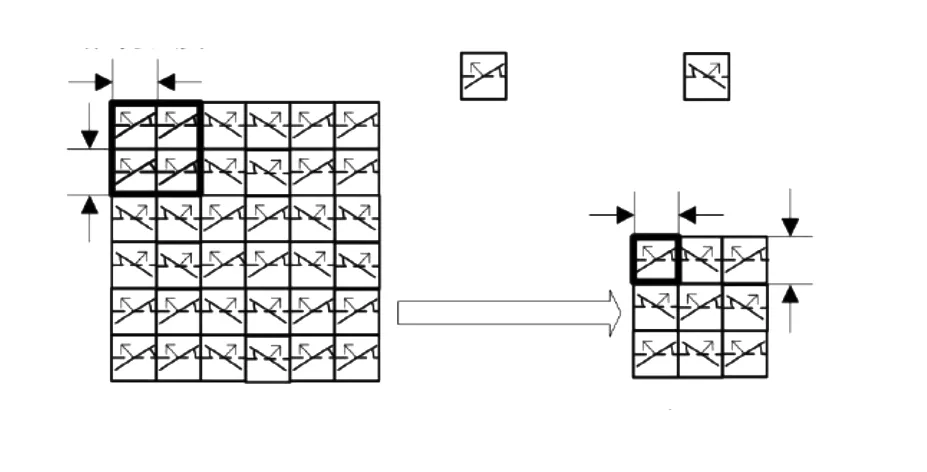
图1 DMD分区控制过程，引自文献[14]。

(1)

由式(1)可知，φi实际上是将φ1i的每个值重复4次后得到的投影矩阵。DMD分区控制减少了采样次数，提高了图像数据获取的准确度[16]，这种分区采样的思想同样可以用于后期小波树结构中图像细节的采样。

2.2 扩展小波树理论

传统自适应压缩采样成像方法由于子系数实际上只包含了父系数所含信息的一部分，即使是绝对值较大的重要的父系数，也有可能对应非重要的子系数，只通过父子关系来采样重要父系数对应的所有子系数，会造成采样资源的浪费。基于此，文献[9]提出了扩展小波树的概念，不仅考虑小波树结构中上下层系数之间的父子关系，同时考虑同层不同高频子带中，相同空间位置处的小波系数之间的兄弟关系[17-19]。图2给出了扩展小波树结构中的父子与兄弟关系。其中，不同层间的单箭头表示父子关系，子带间的双向箭头表示兄弟关系。

图2 扩展小波树结构

图3 单次测量的二进制投影图像。(a)水平方向;(b)垂直方向;(c)对角方向。

(2)

根据扩展小波树结构中小波系数间的兄弟关系，水平和垂直方向的小波系数可以写成两个DMD测量差值之和，如式(3)：

(3)

其中

(4)

由式(4)可知，每一个测量差值都包含了两个对应子系数的信息。如果对角子带上的父系数值已知，那么位于相同尺度、相同的空间位置上的水平和垂直方向的小波系数的两个差值可以通过计算得到，由此判断子系数的重要性。

3 压缩感知与扩展小波树理论的自适应压缩成像方法

基于扩展小波树的压缩采样成像方法[9]，其压缩采样过程主要在于对重要小波系数位置的预测并只采样重要小波系数。对于在小波域稀疏或者可压缩的图像，大大减少了采样量。但其低分辨率的粗糙图像的获得依旧采用的是点对点的采样过程，即对低分辨图像的每个像素进行全采样。本文中对粗糙图像的获取进行了改进，提出了基于压缩感知与扩展小波树的压缩采样方法。由于压缩感知方法获得的仅仅是低分辨率图像，所需计算量以及重构图像所需时间很小，并不会因此增加采样与成像时间。成像方法和流程如下：

基于DMD分区控制与扩展小波树结构的压缩采样流程如图4所示。

图4 基于DMD分区控制与扩展小波树的压缩成像流程图

由于自然图像绝大多数都是可压缩图像，不满足稀疏性，因此利用常用的重构算法很难高质量地恢复图像。因此在低分辨率图像的重构过程中选用最小化全变分算法(TV minimization scheme based on augmented Lagrangian and alternating direction algorithms，TVAL3)算法，该算法不需要投影矩阵满足正交性，在重构过程中能够很好地保留图像的原有轮廓，重构效果好。

4 实验测试与分析

为了对成像质量进行评估，采用峰值信噪比作为评价指标，其计算表达式如(5)式所示：

(5)

其中：

(6)

实验选取灰度图像boat和man作为测试图像。实验中获得粗糙图像所用的初始采样率以及获得最终图像所用的整体采样率对最终的成像质量有着重要影响。为了更好地确定所选参数，本文对两幅图像的参数与成像的峰值信噪比进行了统计分析。图5给出了两幅图像的初始粗糙图像在压缩感知中的采样率与成像峰值信噪比的曲线图，其中采样所得的粗糙图像的分辨率为32×32。

图5 粗糙图像采样率与粗糙图像峰值信噪比关系图。(a)Boat图像；(b)Man图像。

如图5所示，随着采样率的提高，图像信噪比呈现上升趋势，即当采样率达到70%以后，图像信噪比随着采样率的增大，增长速度加快。然而，最终成像除了与初始的粗糙图像质量有关，还与后期的采样情况有关。图6给出了当整体采样率为10%时，最终所成图像的信噪比与粗糙图像的采样率之间的关系。其中横轴为初始粗糙图像的采样率，纵轴为最终图像的峰值信噪比。

图6 粗糙图像采样率与最终峰值信噪比关系图。(a)Boat图像；(b)Man图像。

如图6所示，尽管整体采样率相同，随着粗糙图像采样率的提高，图像信噪比整体呈现上升趋势。说明粗糙图像的质量对整体成像质量非常重要，因为粗糙图像的成像情况影响了后期重要小波系数所在位置的判断，其判断的准确性直接决定了整体成像的质量。由图6可知boat和 man这两幅图像在粗糙图像采样率为0.7～0.8之间时信噪比变化趋缓，达到较高的信噪比。对照图5，当初始粗糙图像的信噪比达到30 dB后，再次提高初始粗糙图像的信噪比对最终成像结果的影响不大。因此选取当粗糙图像信噪比达到30 dB时的压缩感知采样量作为初始采样参数，图7给出了两幅图像在给定压缩感知采样率分别为0.75时的成像结果，第一列、第二列和第三列分别对应的整体采样率为3%、5%和10%。成像分辨率为512×512。

图7中，从视觉角度看，采样率仅为3%时，4幅图像就已经非常清晰了，只有背景区域以及局部少量纹理丰富的区域相对而言较为模糊。为了进一步给出量化评价，表1列出了在不同采样率下两幅图像的信噪比。

图7 不同采样率下的成像结果。(a1～a3)Boat图像整体采样率为3%、5%、10%;(b1～b3)Man图像整体采样率为3%、5%、10%。

表1 不同采样率下两幅图像的信噪比

图8给出了采样率与峰值信噪比之间的曲线关系，其中初始粗糙图像依旧按0.75的采样率通过压缩感知重构获得，信噪比通过多次计算取平均值记录。

结合表1和图8可知，随着采样率的提高，图像信噪比整体呈现上升趋势，其中boat在采样率达到10%后，信噪比的提高速度变缓，说明对于边界清晰、纹理变化相对简单的图像，在一定的采样量范围内，少量细节的增加不影响图像的成像质量。而对于man图像，在头发、头饰、衣服、背景处均存在较为复杂的纹理，随着采样量的提高，不同的纹理区域的获得将越来越清晰，因此在采样率达到某些关键值时，图像信噪比会大幅提高，在个别点处曲线出现的波动主要来源于初始粗糙图像的成像质量的波动。当粗糙图在重构时出现错误，会使得后期小波系数的采样出现可能的偏差，尤其在采样量较大时，这种偏差反而会导致成像质量的降低。

为了验证该算法的有效性，将该算法与压缩感知中的TVAL3算法以及扩展小波树算法EWT-ACS结果进行了比较。图9给出了boat和man图像在3种不同算法下的成像结果。

图8 采样率与信噪比关系图。(a)Boat图像；(b)Man图像。

图9 3种不同算法下的成像结果。a1～a3为boat图像在TVAL3、EWT-ACS及本文算法下的结果;b1～b3为man图像在TVAL3、EWT-ACS及本文算法下的结果；c1～c3为 b1～b3图像放大后的面部图像。

图9中，3种算法的采样率均设置为10%，图像boat在3种不同算法下的信噪比分别为：20.167 4，21.932 3，24.801 2 dB；图像man在3种不同算法下的信噪比分别为：19.392 5，21.680 3，23.976 8 dB。从视觉角度看，TVAL3算法所成图像较为模糊，但整体轮廓的连续性高；EWT-ACS及本文算法整体清晰度更高，但均不同程度地存在一定的块状马赛克现象。由于在相同采样率的条件下，本文算法对细节的采样量更大，因此块状现象相对不明显。这点从放大后的man的面部细节可以看得更加清楚。图9(c2)中在羽毛处有较多的大的块状分布，而图9(c3)，块状分布明显减小，图像边缘的连续性更高。

为了进一步分析该方法受成像过程中的噪声影响情况，在实验中模拟含探测噪声的采样过程，对采样过程添加标准差为25的高斯白噪声。加噪后的boat图像如图10所示，采样率依旧为10% 。

图10 不同算法成像结果。(a)添加噪声后图像;(b)TVAL3算法结果;(c)EWT-ACS算法结果;(d)本文算法结果。

由图10可见，3种算法成像过程由于受噪声影响，图像质量均出现不同程度的下降，(b)～(d)所对应的峰值信噪比分别为20.002 2，17.259 7，20.008 0 dB。其中，EWT-ACS算法受噪声影响最为严重，因为该算法成像过程中，低分辨率的粗糙图像以及小波系数由于都是逐点采样，每次采样均受到较大的噪声影响。TVAL3算法一次采集多个点的像素，在相同强度的噪声下，计算所得的每个像素受噪声影响降低，因此信噪比反而较高。本文算法在获得初始粗糙图像时采用TVAL3算法，受噪声影响小。

5 结 论

为了在获取高分辨率图像的同时减少采样时间，同时降低图像重构的计算量，本文从采样过程出发，提出了一种基于压缩感知与扩展小波树的自适应采样的压缩采样成像方法。实验中，对算法所需参数进行了详细讨论，并与压缩感知算法(TVAL3)和扩展小波树的压缩采样算法(EWT-ACS)的结果进行了比较分析。结果表明，当参数设置为压缩感知采样率0.75，整体采样率为10%时，由具体量化值可知，图像boat在3种不同算法下的信噪比分别为：20.167 4，21.932 3，24.801 2 dB；图像man在3种不同算法下的信噪比分别为：19.392 5 ，21.680 3，23.976 8 dB。本文提出的采样方法所获得的图像效果最好，峰值信噪比最高。

而在模拟含探测噪声的采样过程中，对添加高斯白噪声的boat图像，本文方法与EWT-ACS方法最终获得图像的峰值信噪比分别为17.259 7 dB和20.008 0 dB。因此，当存在噪声影响时，EWT-ACS方法受噪声影响严重，本文方法由于结合了压缩感知算法，有较好的抗噪性。