Ag-Cr共掺LiZnP新型稀磁半导体的光电性质∗

杜成旭 王婷 杜颖妍 贾倩 崔玉亭 胡爱元 熊元强 毋志民

(重庆师范大学物理与电子工程学院,光电功能材料重庆市重点实验室,重庆 401331)

1 引 言

现代信息技术在实现信息的存储时利用了材料的磁性,而对信息的处理则借助了材料的电性,构造将磁、电集于一体的磁性半导体器件是研究人员长期以来的目标[1].要实现磁、电集于一体,不仅要有局域磁矩,还要有能够引发局域磁矩长程量子序的低浓度载流子.于是有研究者尝试用稀土金属或过渡金属的磁性离子取代非磁性半导体中的部分阳离子,便形成了将电子的电荷和自旋两个自由度集于同一基体的材料——稀磁半导体[2].但是在几类已知的传统稀磁半导体中,局域磁矩和载流子都是由同一种掺杂元素提供的,例如广为研究的III-V族的(Ga,Mn)As稀磁半导体[3],由于Ga3+和Mn2+具有不同的价态,Mn2+对Ga3+的替换在引入自旋的同时也引入了p型载流子,自旋和电荷的这种捆绑效应增加了对材料电性和磁性的调控难度.因此,实现稀磁半导体中自旋和电荷注入机制的分离成为研究人员的主要任务之一.

Mašek等[4]采用基于第一性原理的局域自旋密度近似(LSDA)+U的计算方法,发现了I-II-V族基新型稀磁半导体LiZnAs,它与GaAs[5]具有类似的晶体结构,电子能带计算结果表明它们的带隙非常接近,半导体性质相似.但与GaAs不同的是,对LiZnAs在Zn2+位注入Mn2+只引入了自旋,通过改变Li的含量可以对载流子进行调控.王爱玲等[6]通过研究Mn掺杂LiZnAs对材料的影响,发现LiZnAs半导体的磁性和电性可以分别通过Mn的掺入和改变Li的含量进行调控.而LiZnP与LiZnAs的晶体结构相同,Mn掺LiZnP同样能够实现电荷与自旋注入机制的分离[4],同时由于材料矫顽力(∼50 Oe,1 Oe=103/(4π)A/m)很小,这使低场调控自旋和电荷的应用成为可能.尽管Li(Zn,Mn)P的居里温度不高,约为34 K,但其禁带宽度为2.04 eV[7],较LiZnAs的1.61 eV[4]更宽.而已有理论研究表明,随着稀磁半导体晶格参数的减小和能隙的增大,稀磁半导体中载流子自旋和局域自旋之间的交换积分(Jp-d)也会随之增加[8],交换积分越大也就意味着居里温度越高,因此LiZnP基新型稀磁半导体可能比LiZnAs基拥有更高的居里温度.此外,Li(Zn,Mn)P新型稀磁半导体表现出良好的铁磁性,Ding等[9]利用核磁共振实验证实了Li(Zn,Mn)P中的铁磁性来源于Mn-Mn自旋磁矩的长程有序排列.

而Cr和Mn同为3d过渡金属磁性元素,关玉琴等[10]通过研究p型稀磁半导体材料发现,对于同种基质,掺杂不同金属元素时,随空穴浓度的增加,材料的居里温度也随之升高,且掺Cr比掺Mn具有更高的居里温度.Cui等[11]的计算结果表明,在GaN基的稀磁半导体中,Cr的结团对于比较低的平均磁矩有一定的贡献,但结团的Cr原子只存在反铁磁性的基态,因而降低了总的磁矩,增强了平均磁矩.由于研究发现用磁性过渡金属元素掺杂时,体系的铁磁性产生机理和磁沉积问题难以解释清楚,于是有学者开始尝试用非磁性离子进行掺杂,如林竹等[12]采用基于密度泛函理论的平面波基超软赝势法,结合广义梯度近似,发现Cu掺杂AlN后得到的净磁矩为2µB,磁性的产生来源于p-d轨道杂化.Ag与Cu为同族元素,吴子华等[13]通过实验制备Ag-ZnO纳米复合材料,研究表明,Ag化学性质稳定,电导率高,且为非磁性离子,在掺杂ZnO时可以得到光学性质较好的p型材料,同时还可以增加复合材料的声子反射,降低材料的热导率.邓军权等[14]采用基于密度泛函理论的第一性原理平面波超软赝势法,发现Ag掺入AlN后,Ag 4d态电子与其邻近的N 2p态电子发生p-d杂化,引入杂质带形成受主能级,实现p型掺杂,使体系的导电能力增强,同时体系表现出金属性和弱磁性,其净磁矩1.38µB.Chen等[15]成功合成了Co-Mn共掺的Li(Zn,Co,Mn)As新型稀磁半导体,发现单掺Co和单掺Mn时均无铁磁有序,但在Co-Mn共掺的情况下,TC=40 K时会出现铁磁有序.

基于此,本文采用基于密度泛函理论的第一性原理计算方法对非磁性元素Ag、磁性元素Cr掺杂LiZnP新型稀磁半导体体系进行了研究.首先采用平面波超软赝势法对24原子超晶胞LiZnP,LiZn0.875Ag0.125P,LiZn0.875Cr0.125P和LiZn0.75(Ag0.125Cr0.125)P体系进行了几何结构优化,计算了Ag单掺、Cr单掺和Ag-Cr共掺LiZnP体系的能带结构、自旋轨道态密度、形成能、电荷重叠布居数和光学性质等,发现用非磁性元素Ag单掺后,材料表现为金属顺磁性;磁性元素Cr单掺后,sp-d杂化使态密度峰出现劈裂,体系变成金属铁磁性;而Ag-Cr共掺后,其性质与Ag和Cr单掺完全不同,变为半金属铁磁性,且共掺时各原子与晶胞原子间的键合作用较强,晶胞的稳定性较好,净磁矩减小,形成能降低,Ag 4d态电子在费米能级附近由完全对称变为明显劈裂.掺杂体系的复折射率函数和介电函数虚部均在低能区出现新的峰值,且Ag-Cr共掺时峰值最高,说明共掺体系加强了对低频电磁波吸收.

2 模型结构与计算方法

2.1 模型构建

理想的LiZnP属于反萤石结构,空间群为F-43m[16,17],晶格参数为a=b=c=0.5765 nm,其中c/a=1.0.构建模型[4]时,将LiZnP看作一个闪锌矿结构的[ZnP]−二元复合(类似GaAs),然后在邻近P四面体间隙填上Li,这样阴离子P呈立方密堆积,阳离子Li,Zn则填充在四面体间隙中,阴阳离子的配位数分别为4和8.LiZnP是稳定的直接带隙半导体[4],可以通过元素Li,Zn,P的高温反应生长制备.文中的计算基于2×1×1(24个原子)的超晶胞模型,每个超晶胞包含的Li,Zn和P原子均为8个.掺杂时采用原子替代法,分别由Ag替换Zn,Cr替换Zn以及Ag与Cr在不同位置替换Zn三种方式来实现掺杂,Ag-Cr共掺时,考虑到Ag和Cr之间可能存在相互作用,为使它们间的相互作用力降到最低,因此在晶胞内部掺杂一个Cr原子,在晶胞的基矢轴上掺杂一个Ag原子,超晶胞模型如图1所示.在计算电子结构和光学性质之前,首先对各种掺杂的LiZnP结构进行了几何优化,以获得最优结构.

2.2 计算方法

图1 24原子超晶胞结构图 (a)LiZnP;(b)LiZn0.875Ag0.125P;(c)LiZn0.875Cr0.125P;(d)LiZn0.75(Ag0.125Cr0.125)PFig.1. The supercell structures of the 24 atoms:(a)LiZnP;(b)LiZn0.875Ag0.125P;(c)LiZn0.875Cr0.125P;(d)LiZn0.75(Ag0.125Cr0.125)P.

采用Material Studio 6.0软件包中的从头算量子力学程序(Cambridge serial total energy package,CASTEP)[18]完成本文的计算工作.计算中采用周期性边界条件,利用LSDA处理电子之间的交换关联能.为了减少平面波基矢组展开个数,价电子与离子实之间的相互作用采用平面波基超软赝势法[19]来描述.计算中选取Li,Zn,P,Ag,Cr的价电子组态分别为Li 1s22s1,Zn 3d104s2,P 3s23p3,Ag 4d105s1,Cr 3d54s1.为了得到可靠的计算结果,开始计算时选用了不同的平面波截断能(Ecut)来计算纯LiZnP的晶格常数和自由能,发现当Ecut=480 eV时体系各项参数趋于定值而达到收敛.因此,在倒易的K空间,文中所有的计算都选取Ecut=480 eV为平面波截止能.电荷密度和体系总能在布里渊区(Brillouin)的积分计算采用Monkhorst-Park[20]方案,超晶胞体系中K网格点取为4×4×2,以确保体系能量和结构在准完备平面波基水平上的收敛,其自洽场循环收敛精度为2×10−6eV/atom.选用Broyden-Fletcher-Goldfarb-Shanno[19]算法对结构进行优化,其原子之间相互作用力收敛标准为0.5 eV/nm,原子总能量收敛精度为2.0×10−5eV/atom,晶体内应力收敛标准为0.1 GPa,原子的最大位移收敛精度为2.0×10−4nm.为使计算结果更加精确,计算中首先对晶胞结构进行优化,根据所得晶胞参数再对内坐标进行优化,晶胞结构优化之后的各项参数均优于收敛标准.

3 晶格结构

为了与掺杂体系的电子结构进行分析比较,首先利用LSDA对纯LiZnP超晶胞进行了几何结构优化,所得晶格常数、带隙和总能如表1所列.可以看出,优化后LiZnP的计算值和实验值[7]之间符合较好,c/a=0.9989,与实验值1.0[7]基本符合,说明采用的计算方法是切实可行的.但计算的带隙值为1.027 eV相比实验值2.040 eV[7]仍有差距,主要是因为计算中采用的密度泛函理论为基态理论,而能隙属于激发态,故计算出来的带隙值偏低[21].在本文中LiZnP体系计算得到的带隙值偏低主要是因为计算时高估了Zn 3d态电子的能量,造成Zn 3d态电子与P 3p态电子的相互作用增大,导致价带带宽增大,带隙值偏低,但这并不影响对本征LiZnP和掺杂体系的电子结构及相关性质的分析.

表1 LSDA优化后本征LiZnP的晶格常数、带隙与总能Table 1.The lattice constant,band gap,and total energy of LiZnP optimized with LSDA.

表2为Ag单掺、Cr单掺和Ag-Cr共掺LiZnP体系所计算得到的晶格常数和体系总能.由表2可以看出,Ag单掺LiZnP体系的晶格常数略有增大,且a,b,c方向基本一致,这主要是由于Ag的离子半径比Zn的大,同时Ag的电负性比Zn的电负性要弱,在Ag替代Zn后与P形成了较强的共价键,这样Ag—P键就比Zn—P键的键长更长,而Cr单掺时其对应方向晶格常数略有减小.当Ag-Cr共掺时a,b方向晶格常数与纯LiZnP体系的晶格常数接近,但c方向的晶格常数增大,主要是因为在共掺情况下,杂质原子Ag和Cr之间有相互作用,这一计算结果与文献[22]的理论和实验结果一致.

表2 Ag,Cr单掺和Ag-Cr共掺LiZnP的晶格常数和总能Table 2.The calculated lattice constants and total energies of Ag doped,Cr doped and Ag-Cr co-doped LiZnP.

4 磁电性质

4.1 Ag单掺LiZnP的能带结构和态密度

图2是本征LiZnP超晶胞的能带结构和态密度图.由图2(a)可以看出,纯LiZnP为直接禁带半导体,价带顶和导带底位于布里渊区的高对称点G点处,带隙值为1.027 eV.结合态密度可以看出,体系价带主要是由P 3p态和少量的Li 2s,Zn 3d态电子构成,导带主要是由Zn 4s,P 3s态及少量的Li 2s态电子构成.由图2(e)总态密度图可以看出体系自旋向上和自旋向下的能带结构完全对称,对外不显磁性.

图3为非磁性元素Ag单掺LiZnP的能带图和态密度图.图3(a)能带图中费米能级下移进入价带,带隙值为1.068 eV(表4),比纯LiZnP的带隙值1.027 eV略大,这主要是因为Ag掺入后电子数增多,使能带图中出现与Ag有关的杂质带.费米能级贯穿于杂质带中,材料整体变为金属性.结合态密度图3(b)—(e)可以看出,体系价带主要由P 3p态以及少量的Li 2s,Zn 4s,Ag 4d态电子组成,价带顶的位置由P 3p态电子决定.导带呈现两个态密度峰,主要由Zn 4s,P 3p态电子以及少量的Li 2s,P 3s,Ag 5s态电子构成.费米面附近的态密度主要是由Ag 4d态电子和P 3p态电子贡献,但P 3p态电子的作用要远大于Ag 4d态电子的作用,两者之间没有形成强烈的杂化峰.体系自旋向上和自旋向下的态密度图完全对称,对外不显磁性,说明Ag未被自旋极化,而是以金属离子的形式掺入半导体LiZnP中,使Ag单掺LiZnP整体呈现金属顺磁性.

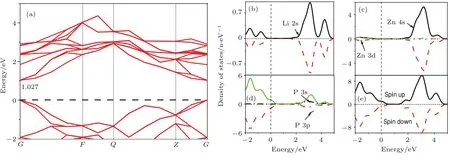
图2 LiZnP超晶胞的(a)能带结构图、(b)—(d)分波态密度图和(e)总态密度图Fig.2.(a)The band structure,(b)–(d)partial density of states,and(e)total density of states of pure LiZnP supercell.

图3 Ag单掺LiZnP的(a)能带结构图、(b)—(e)分波态密度图和(f)总态密度图Fig.3.(a)The band structure,(b)–(e)partial density of states,and(f)total density of states of Ag doped LiZnP.

4.2 Cr单掺LiZnP的能带结构和态密度

图4为磁性元素Cr单掺LiZnP的自旋极化能带图和态密度图.由图4(a)和图4(b)可知,对比Ag单掺,发现Cr单掺时其在带隙中引入了与Cr相关的自旋极化杂质带,自旋向上和自旋向下各5条,其中自旋向上的5条较离散,有两条并入价带,剩余3条跨过费米能级,表现出一定的金属性;而自旋向下的5条杂质带,其中4条位于费米能级上方,1条跨过费米能级,也表现为金属性,从而体系整体上表现为金属性质.图4(c)—(f)是Cr单掺时的态密度图,可以看出在费米面附近自旋向上和自旋向下的电子态密度分布劈裂,究其原因是Cr掺入后,在费米能级附近Li 2s态电子和P 3p态电子出现新的峰,与Cr 3d态电子的态密度峰重叠,使得Li 2s,P 3p,Cr 3d电子轨道发生了强烈的sp-d杂化作用.从图4(g)总态密度图可以看出自旋向上的电子态密度跨过费米能级,而自旋向下的电子态密度在费米能级处张开一个能隙,且自旋向上与自旋向下不对称,对外显磁性,磁矩为4.0µB,使Cr单掺后体系变为金属铁磁性.

图4 Cr单掺LiZnP的(a),(b)自旋极化能带图,(c)—(f)分波态密度图和(g)总态密度图Fig.4.(a),(b)The spin polarized energy band,(c)–(f)partial density of states,and(g)total density of states of Cr doped LiZnP.

4.3 Ag-Cr共掺LiZnP的能带结构和态密度

图5为Ag-Cr共掺LiZnP的自旋极化能带图和态密度图.图5(a)和图5(b)是Ag-Cr共掺时的能带图,可以看出共掺体系为半金属化合物,其能带结构与Ag单掺和Cr单掺LiZnP完全不同,其自旋向上跨过费米能级,表现出金属性,但自旋向下未跨过费米能级,表现出半导体性质(带隙值为2.024 eV),从而整体表现出半金属性,半金属能隙为0.493 eV,杂质带宽度为0.609 eV.图5(c)—(h)是Ag,Cr共掺的态密度图,可以看出在费米能级附近跨过费米能级的子带主要是自旋向上的P 3p,Cr 3d态电子以及少量的Li 2s态,Ag 4d态电子.与Ag单掺LiZnP对比,Ag 4d态电子出现明显的劈裂,说明Ag原子产生自旋极化并且表现为弱磁性;对比Cr单掺LiZnP的态密度图可以发现,Li 2s,P 3p和Cr 3d跨过费米能级的态密度均增大,表明Ag-Cr共掺使体系sp-d杂化增强,体系变为半金属铁磁性.费米面附近的态密度分布决定着物质的磁性,对费米能级以下的占据态进行积分计算之后得到的结果表明自旋向上的电子数要比自旋向下的电子数多,计算得出Ag-Cr共掺LiZnP体系总磁矩为3.06µB(表4),其中Cr贡献3.26µB,P贡献−0.54µB,Zn贡献0.24µB,Ag贡献0.1µB.

图5 Ag-Cr共掺LiZnP的(a),(b)自旋极化能带图,(c)—(g)分波态密度图和(h)总态密度图Fig.5.(a),(b)The spin polarized energy band,(c)–(g)partial density of states,and(h)total density of states of Ag-Cr co-doped LiZnP.

5 差分电荷密度及形成能

表3为掺杂体系原子间的重叠电荷布居和键长.重叠电荷布居数可以用来判断原子间键的种类和键强度的大小,布居数中的正值代表共价键,数值越大,共价键越强;负值代表离子键,负值越小,原子间的排斥作用越大,原子间的相互作用和键强度越弱,晶胞的稳定性越差.从表3可以看出,在LiZnP晶胞中,Zn—P键的电荷布居重叠数为正值,但Li—P键呈离子键,化学键总体表现为极化的共价键[23].单掺Ag时,Li—P,Zn—P键的重叠电荷布居未发生任何的变化,这与能带图中Ag掺杂体系未发生自旋极化一致,Li—P键的键长增加到2.450 Å,而Zn—P键的键长有所减小.单掺Cr时,Zn—P键的重叠电荷布居为0.75,而Cr—P的重叠电荷布居为0.84,表明Cr与P的电子间发生了强烈的相互作用,形成了强于Zn—P键的Cr—P共价键,且Li—P,Cr—P键的键长均有所减小,这与晶格常数减小相对应.而Ag-Cr共掺后,Cr—P键的电荷布居最大,且键长最小,相互作用最强,使得Ag-Cr共掺时呈现半金属性,该相互作用体现为轨道之间的杂化作用,与态密度结果一致.

掺杂前后各体系的差分电荷密度如图6所示,借助差分电荷密度图,可以分析各原子之间电子的分布和转移情况[24].图中白色代表得到电子,黑色代表失去电子,灰色代表没有电子的得失.通过对比掺杂前后的四种情况发现,随着杂质原子的掺入,原子之间的成键性质差异很大,原子之间的相互作用也不相同,体系之中的电荷重新分配.

由图6(a)可以看出,本征LiZnP中Zn原子和P原子之间存在着共价键,Li原子与其临近的P原子之间存在着包含共价键成分的离子键.LiZnP晶胞在两种键的共同作用下得到强化,原子交叠处的电子云出现了分布不均匀的情况.由图6(b)可知,单掺Ag时,靠近Ag位置的电子云比靠近Zn位置的电子云更密集,这主要是由于Ag的电负性弱于Zn;由图6(c)可以看出,单掺Cr时,黑白色分布明显加强,说明Cr和P原子之间的共价键加强,靠近Cr的位置的P原子电子云更密集,主要是Cr与P之间形成极化共价键且共用电子向P偏转所致.由图4分波态密度可知,极化共价键主要是由Cr的3d态与P的3p态形成.图6(d)表明,当Ag-Cr共掺的情况下,P原子靠近Cr原子位置的电子云最密集,且共用电子偏移程度最小,因此Cr与P的杂化作用最强;Ag—P之间的共价键减弱,而Cr—P共价键有所增强,且Ag原子与其临近的Cr原子之间共价键加强,原子间的作用力增大,增强了体系的稳定性.

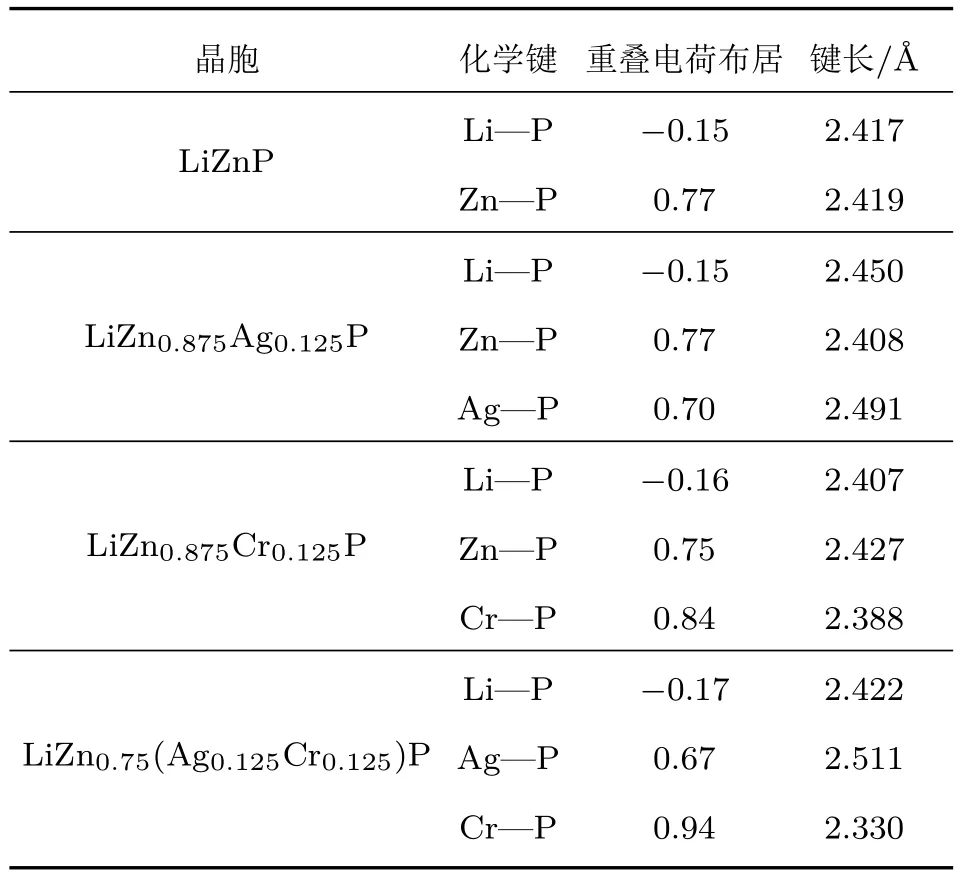
表3 掺杂体系原子间的重叠电荷布居和键长Table 3.Charge population and bond length of the doped systems.

掺杂体系的稳定性可根据体系的形成能Ef[20]来判断:

其中E表示计算的体系总能,n表示改变的原子个数,µ表示化学势.化学势的取值受实验条件的影响,但这里旨在比较各掺杂体系基态的相对稳定性,所以Ag,Cr,Zn的化学势选取为在电中性情况下各单质在稳定结构中的能量.本文计算了各掺杂体系的形成能,结果如表4所列.可以看出,单掺Ag后LiZnP体系稳定性与纯LiZnP较为接近,在掺杂体系中最低,而单掺Cr时体系的形成能最高,Ag-Cr共掺后,形成能有所降低,体系稳定性相应地有所提高,说明Ag的掺入可以提高体系的稳定性.

图6 掺杂体系典型晶面(110)的差分电荷密度图 (a)LiZnP;(b)Li(Zn0.875Ag0.125)P;(c)Li(Zn0.875Cr0.125)P;(d)Li(Zn0.75Ag0.125Cr0.125)PFig.6. Difference charge density of the typical crystal surface(110)of the doped system: (a)LiZnP;(b)LiZn0.875Ag0.125P;(c)LiZn0.875Cr0.125P;(d)LiZn0.75(Ag0.125Cr0.125)P.

表4 掺杂体系的带隙、杂质带宽度、半金属能隙、磁矩和形成能Table 4.Band gap,impurity band width,half metal energy gap,magnetic moment and formation energy of the doped systems.

6 光学性质

分析材料的光学性质可以作为研究电子结构等有关物理性质的有效补充.本文计算了掺杂前后LiZnP体系的复折射率函数、介电函数虚部、能量损失谱和光吸收谱.根据半导体光学性质,利用直接跃迁定义和Krames-Kronig色散关系可以得到掺杂体系的介电函数虚部、反射率、吸收系数、复折射率等参数[24].在线性响应范围内复介电函数可以用来描述半导体材料的宏观光学性质:

其中,

纯LiZnP和掺杂体系的复折射率函数如图7(a)所示,纯LiZnP在E<1 eV的低能区和E>15 eV的高能区虚部n(εi)为0,而实部n(εr)趋于常数,表明LiZnP体系对过低频和过高频的电磁波的吸收均较弱,吸收限制在一定的范围内.单掺Ag后复折射率函数在高能区吸收边发生了轻微蓝移,在低能区实部有微小变化,而虚部有明显的变化,出现了一个小的杂质峰,这是由于sp-d轨道杂化使能带偏移造成的,增大了体系对低频电磁波的吸收.单掺Cr后,其实部和虚部在低能区的变化更剧烈,说明Cr单掺进一步增大了对低频电磁波的吸收范围和强度.Ag-Cr共掺后,在低能区的实部和虚部在强度上均比单掺时明显增大,表明共掺体系对低频电磁波的吸收效果最明显.

图7(b)为介电函数虚部,图中纯LiZnP的介电函数虚部主要有对应光子能量为E=4.8 eV的介电峰,纯LiZnP是直接带隙半导体,光谱的产生来源于能级间的跃迁,其介电峰的来源可借助态密度和能带结构来分析[22],对比纯LiZnP的态密度可知,这对应着体系的直接跃迁,是价带P 3p态电子向导带Li 2s态和Zn 4s态跃迁的结果.单掺Ag后,在0—3 eV之间新出现了一个很小的介电峰,对应的能量为1.2 eV.Cr单掺和Ag-Cr共掺LiZnP后,与单掺Ag相似,在低能区都出现了新的介电峰,分别对应峰1和峰2.介电峰都向低能方向移动是由于Cr的掺入使光学能隙增大,而峰1、峰2的峰值明显增强,且峰2峰值最高,这是由于Cr原子的3d态电子与P 3p态、Li 2s态电子发生剧烈的sp-d杂化作用,且介电函数虚部的图像较纯LiZnP和Ag单掺LiZnP体系明显变宽,与能带图中Cr单掺和Ag-Cr共掺后带隙明显变宽相一致.

图7 Ag,Cr掺杂LiZnP前后的(a)复折射率函数和(b)介电函数虚部Fig.7.(a)The complex refractive index functions and(b)imaginary parts of dielectric functions before and after Ag and Cr doped LiZnP.

图8 Ag,Cr掺杂LiZnP前后的(a)能量损失谱和(b)光吸收谱Fig.8.(a)The energy loss spectra and(b)absorption spectra before and after Ag and Cr doped LiZnP.

图8(a)为能量损失谱,能量损失谱可以用来描述电子在通过均匀电介质时的能量损失情况,能量损失峰则被用来描绘等离子的共振频率[25].据图8(a)可知,纯LiZnP的损失峰位于13.13 eV附近,单掺Ag后损失峰发生蓝移,即向高能方向有所偏移,相比纯LiZnP其能量损失最大,单掺Cr后能量损失略有减小,而Ag-Cr共掺后损失峰略微有偏移,但能量损失进一步增大.图8(b)为掺杂前后的光学吸收谱,可以看出在40 nm以上吸收峰基本相符,只是吸收峰略微向长波方向延展,这和掺杂之后体系的带隙值变大,介电函数的吸收边发生红移相符合.但分析20—40 nm处的放大图发现,对比纯LiZnP、单掺Ag,在单掺Cr和Ag-Cr共掺时吸收谱在25 nm附近出现了新的吸收峰,这是由于Cr 3d态电子与P 3p态、Li 2s态电子的相互作用而产生的.

7 结 论

本文采用基于平面波超软赝势法和LSDA的第一性原理计算方法,对纯LiZnP,Ag单掺LiZnP,Cr单掺LiZnP和Ag-Cr共掺LiZnP体系的24原子超晶胞进行几何结构优化,计算并分析了掺杂前后体系的电子结构、能带、态密度、磁性、差分电荷密度、形成能以及光学性质.结果表明,Ag单掺后体系整体表现为金属性,Ag未被自旋极化,自旋向上和自旋向下的态密度完全对称,体系内无净磁矩对外不显磁性;单掺Cr时,体系引入自旋极化杂质带,整体表现出金属铁磁性,磁矩为4.0µB,且形成了强于Zn—P键的Cr—P共价键.Ag-Cr共掺时,与Ag和Cr单掺时完全不同,Cr—P键的电荷布居最大,且键长最小,相互作用最强,体系整体变成半金属铁磁性;与Cr单掺对比,其磁矩减小为3.06µB,但形成能相对降低,表明Ag的掺入可以提高体系的稳定性.光学性质计算结果表明,随着杂质元素的掺入,掺杂体系的介电函数虚部在低能区出现了新的介电峰,且随着sp-d杂化程度增强,Ag-Cr共掺时新峰的高度最大;复折射率函数在低能区发生较大变化,且Ag-Cr共掺时,其对介质密度的影响最大;掺杂体系的吸收峰均向长波方向扩展,单掺Cr和Ag-Cr共掺时在短波方向引入两个新的吸收峰,表明体系对低频电磁波吸收增强.