WSN中基于信道传播特性的室内跟踪定位算法
李 颖,郑新旺,何雨青,胡妮娜,杨光松
(1.集美大学诚毅学院,福建 厦门 361021;2.集美大学信息工程学院,福建 厦门 361021)
0 引言
传感网在室内定位场景中,需要对一些特殊目标进行跟踪和定位,例如会场特定排座、商品陈列单位立停人数测量、视觉障碍者移动支援、步行者导航、危急监测自动定位报警、室内机器人控制等[1]。如,文献[2]利用参考数据和测量接收信号强度指示(received signal strength indication,RSSI)的数据来找寻室内最有可能的运动轨迹作为序列检查区域,同时结合最大似然度量法进行序列检测来实现运动跟踪定位;文献[3]借助最大似然法估算静态参数来实现传感器的同步定位和跟踪;文献[4]提出一种基于拓扑信息重建多维欧几里得空间里节点的方法,借助最大似然法来实现节点重建和定位。这些研究提出的算法没有考虑信道的影响因素。然而在实际电磁环境中,特别是室内环境,由于建筑结构和使用材料的原因,存在反射、散射、多径等影响[5],使用传统的方法,如到达时间定位法、接收信号角度定位法存在一定的局限性。对于RSSI定位算法,接收电波的强度不仅取决于节点之间的距离,而且会受到信道传播特性的影响。经典的传播模型包括瑞利模型和莱斯模型。瑞利模型描述了小规模快速振幅波动下的衰落变化,它假定所有信号到达接收器时都具有相同的强度,没有考虑直射信号,这与现实情况存在差异。莱斯模型除了分析低电平分散的路径,还考虑存在一条稳定的直射路径。该模型需要从物理上隔离其直射波,但确定其参数有一定难度。
为了提高定位精度,需要研究无线传播特性,统计接收电波强度的概率分布,根据概率模型来预测目标的位置。文献[6]考虑了经典的WAF模型[7]结合传感网和RFID进行节点定位;文献[8]基于人体穿透损耗模型的RSSI测距方法结合卡尔曼滤波算法[9]实现狭长空间的跟踪定位;文献[10]基于RSSI的LANDMARC算法[11]结合距离损耗模型确定虚拟参考标签[12]的场强值以提高室内定位精度。但关于室内环境的无线传播特性的相关探讨较少,本文对无线传输特性的概率进行室内环境建模研究。通过多种不同环境下的实验,利用信道概率统计的方式,并使用最大似然法进行统计推测,提高位置监测定位的精度。
1 最大似然法及传播特性建模
1.1 最大似然法
L(θ)=L(θ;x1,…,xn)=f(x1,…,xn;θ)
(1)
在f(x1,x2,…,xn;θ)中,以x1,x2,…,xn作为变量,使似然函数L(θ)最大的值,就是θ的值。用这种方法推断θ的值,称为最大似然法(ML,maximum likelihood)。
如果x1,x2,…,xn相互独立,则满足
(2)
为使L(θ)最大,求解方程∂lgL(θ)/∂θ=0。当然,也可以转化为求lgL(θ)的形式。当存在k个参数θ=(θ1,θ2,…,θk)的场合,求解方程式∂lgL(θ)/∂θi=0(1≤i≤k)。
1.2 传播特性建模
由于实际环境中的无线传播特性存在变化,需要建立其信道模型,通过多次采样,对信道进行概率化测量统计。首先,通过改变无线节点间的距离并测量接收电波强度,得到节点之间的距离和接收电波强度的关系。随着环境的动态变化,可以推算出无线节点测量信息之间的关系。其次,考虑无线传播特性进行实时传播环境的模型化,假设发送和接收节点之间的距离为d,使L(θ)最大便可求得θ,获得实际中移动节点的运动速度、前进角度和位置坐标。
接收端的平均接收功率的信号强度
(3)
其中,常数c和衰减系数α是传输模型化的参数,对锚节点到信标的距离以及接收功率的信号强度(d,P)进行多组采样测量,可以拟合求得c和α。
信息与计算科学专业是数学、信息科学和计算机科学三者交叉的学科,它以数学为基础,计算机为工具,解决信息和工程计算方面的实际问题.这一专业设置较好地适应了以信息技术为核心的全球经济发展格局下的人才培养与专业发展[1-4].
f(z)=βmzm-1e-βzm(z≥0;m;β>0),
(4)
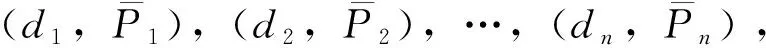
2 基于信道特性的跟踪定位算法
2.1 网络模型
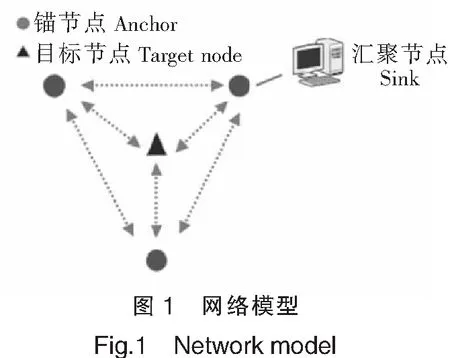
网络模型如图1所示,假设通信区域内布置n个固定的锚节点Ai(i=1,2,3,…,n),锚节点间可以用有线或无线的方式进行通信,最终把数据汇聚到Sink进行集中处理。假设对每个移动的目标节点分配全网唯一的ID,以相同的功率定期向锚节点发送信标。Sink根据各锚节点的准确位置以及接收到目标移动节点Tj(j=1,2,3,…,m)的ID、接收时间、位置、接收功率,从而推测信道条件和目标节点的相关信息。锚节点在接收到目标的信息后,向Sink节点报告。Sink根据收到的目标节点的情报,根据特定算法进行位置推测。考虑移动目标的耗电,一般复杂的位置推测算法,在锚节点一端进行。
2.2 基于最大似然法的跟踪定位协议
根据接收功率的大小,提出基于最大似然法的定位方法,综合考虑信道特性,推测目标的位置、速度和前进方向。
移动终端称为目标,一边移动一边在规定时间间隔内发送n个信标被l个锚节点接收。此时,目标发送的第i个信标被位于(xa,j,ya,j)的锚节点j接收,其接收功率为Pi,j(1≤i≤n,1≤j≤l)。
假设目标作匀速直线运行,速度v,行进方向a。在推测位置时,目标的实际位置用(x,y)表示,第i个信标的发送时刻与推测时刻的差值表示为Δti,信标i被锚节点j接收的功率为Pi,j,其条件概率密度为p(Pi,j|v,a,x,y),按式(3)、(4)求得xi=x-vΔticos(a),yi=y-vΔtisin(a),
j个锚节点接收第i个信标的功率为随机变量Pi,j,如果(P1,1,…,Pn,l)是相互独立的,取参数θ=(v,a,x,y),用似然函数式
(5)
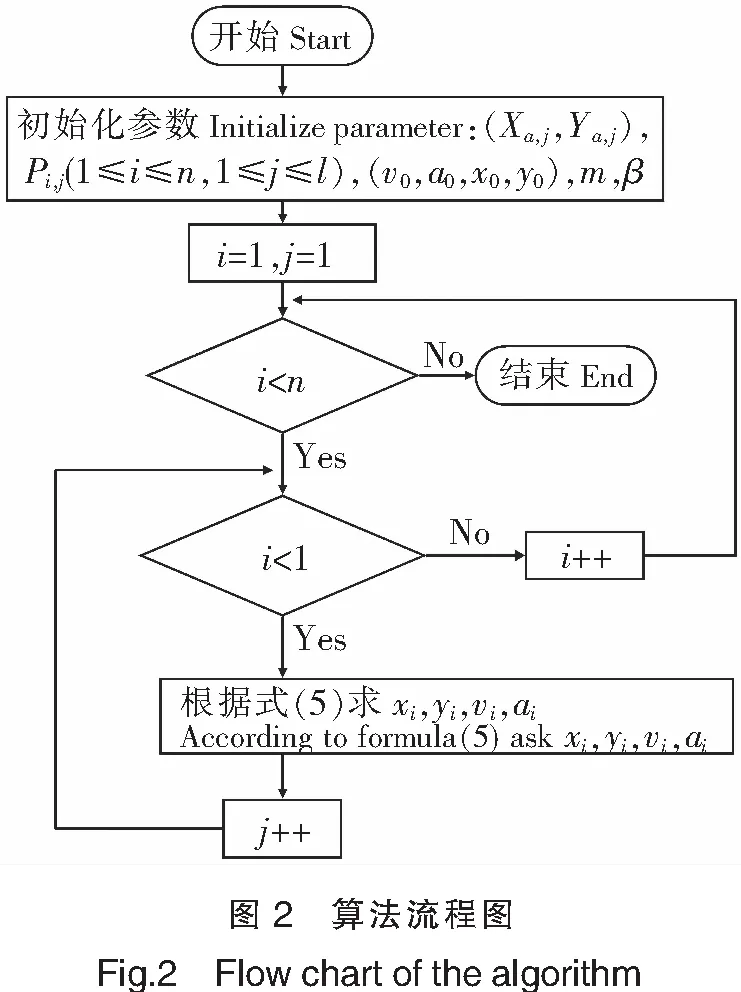
和最大似然法,求解目标的位置、速度和前进方向。其算法如图2所示。
3 信道模型测量
按参考文献[13]的测量方法,设置下列三种场景(见图3):
场景1:封闭走廊,两边都有墙,高2.8 m,宽2.7 m。在走廊中线,每隔1.5 m进行一次信号的测量。
场景2:开放走廊,一侧开放,另一边有一堵墙,高2.8 m,宽4.5 m。每隔1.5 m在走廊的中线进行一次信号的测量。
场景3:实验室,配有家具和计算机,高2.8 m,长15 m,宽10 m。沿着实验室的对角线每隔1.5 m 进行一次信号测量。
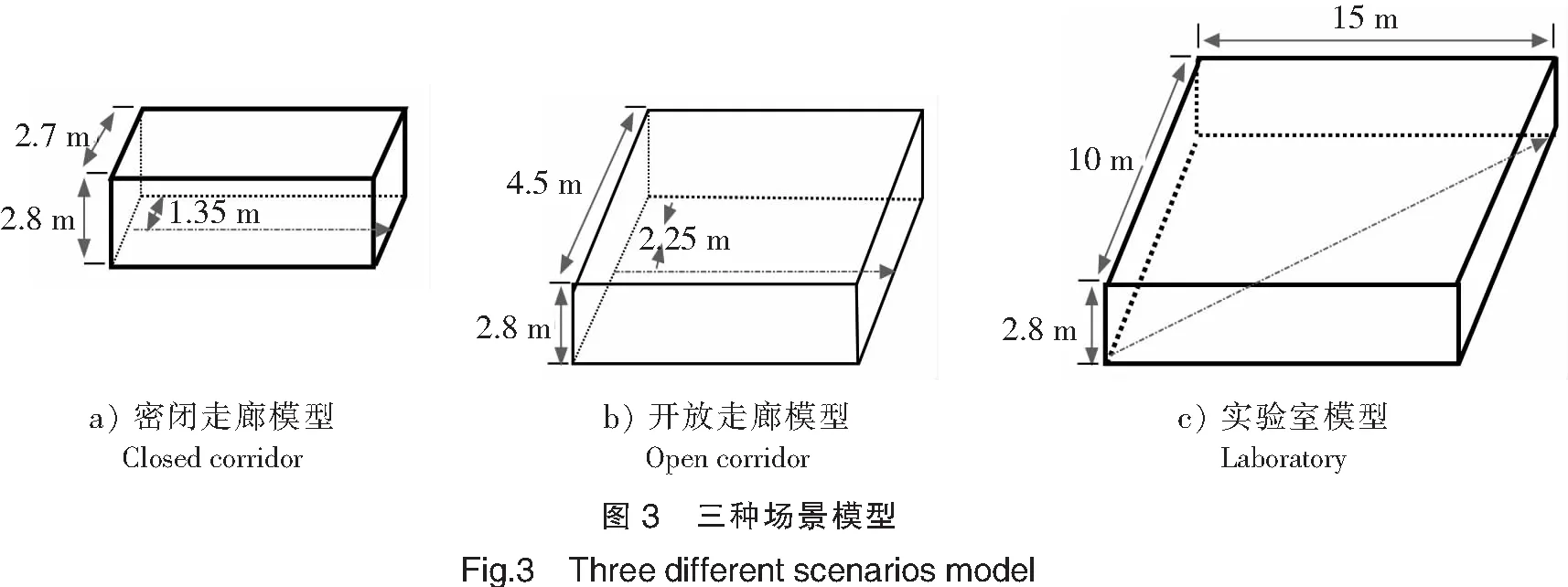
发信机为一个D-Link的无线路由器,使用IEEE 802.11b协议,频率为2.4 GHz,速率为11 Mbite/s依次放在封闭走廊中线起点、开放走廊中线起点和实验室对角线起点。移动笔记本电脑,用Wireless Mon软件测量信号强度。不同场景下,沿着设定路线(见图3中点划线箭头),每隔1.5 m进行10组功率信号强度的采样,根据采样数据,借助最大似然法推测信道传播特性,其测量结果如图4所示。
根据式(3)和式(4)计算其传播特性,结果如表1所示。

表1 三种不同场景下传播特性比较Tab.1 Channel propagation characteristics under three different scenarios
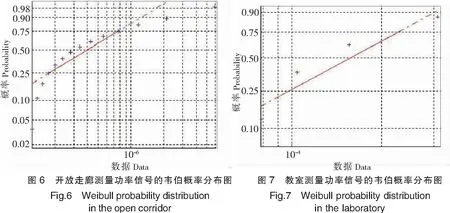
三种场景传播特性的差异由表1、图5、图6和图7表示,其中,符号“十”表示“接收到功率信号”,虚线表示韦伯分布曲线。由此可知,测量数据结果基本符合韦伯分布规律。

4 算法仿真及评估
根据测量结果,获得信道数据,建立对应的信道模型。在Matlab下对三种场景进行仿真验证。对于场景1和场景2,目标节点分别从走廊的其中一个端点向另一个端点移动,锚节点分别设置在两个端点和中点;对于场景3,目标节点沿着对角线移动,锚节点设置在实验室的四个角,移动速度为1 m/s。采用2.2提出的算法,每1 s采集一次接收功率信号强度,运用最大似然法根据样本数据推测移动节点的轨迹。
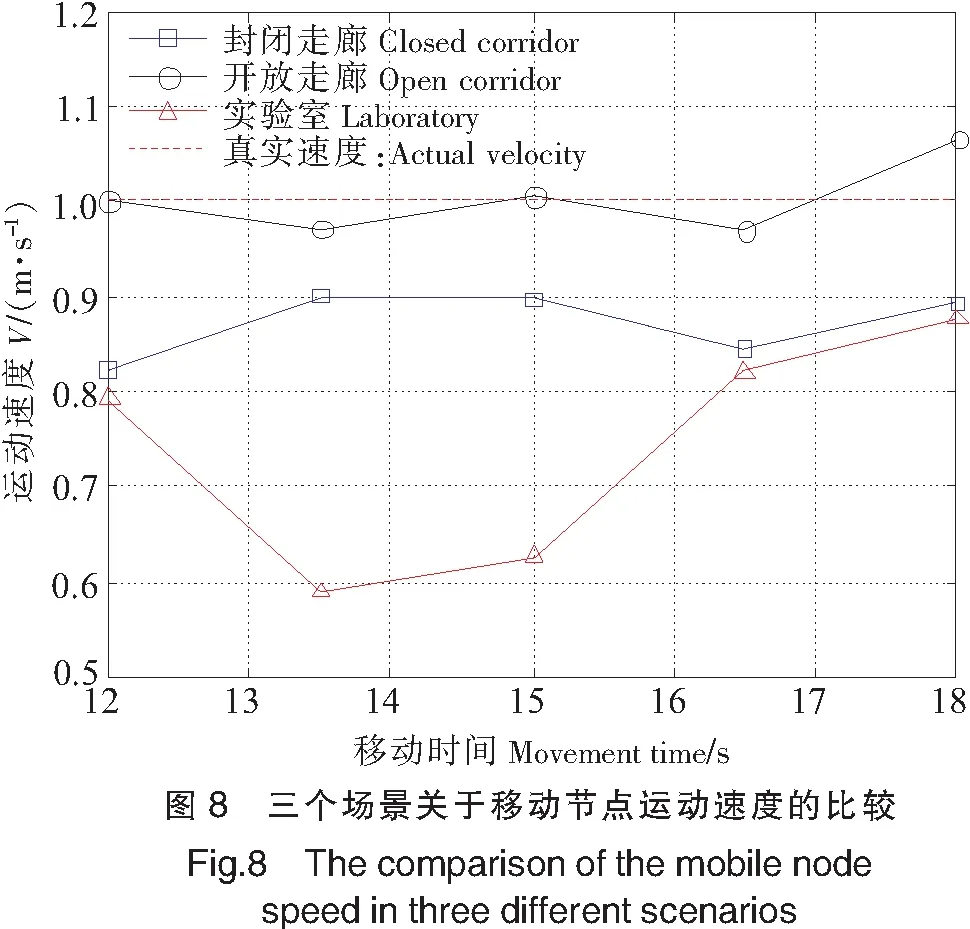
任意取一段时间进行统计,图8至图10分别为三个场景中速度、角度和节点坐标误差在12~18 s这段时间内的估算值。
由图8可知,三者的移动速度都比较接近实际速度1 m/s。其中场景3移动速度偏离实际值最大,场景2移动速度与实际值最为接近。
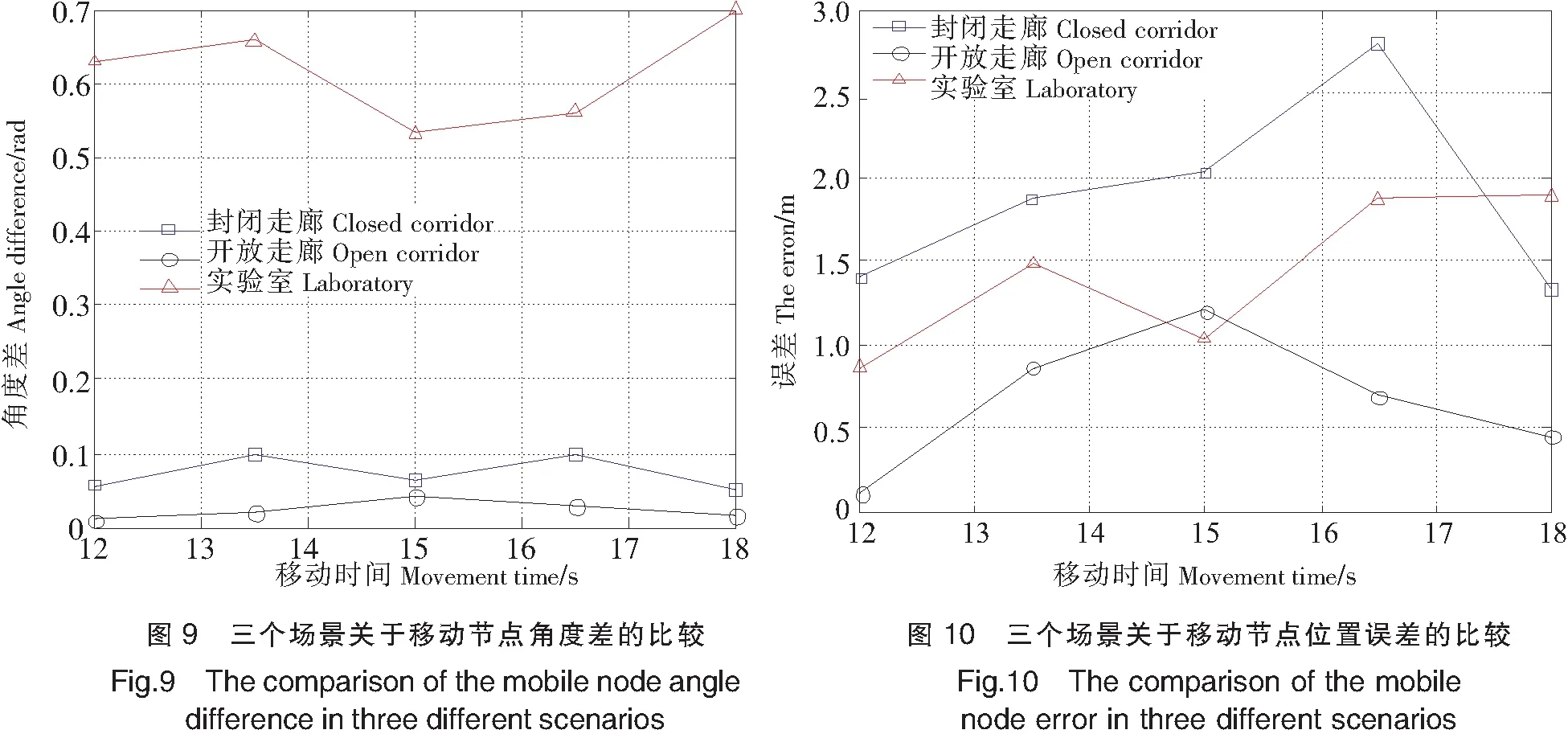
由图9可知,随着移动时间的增加,场景3移动角度为0.54~0.69 rad,场景1和场景2移动角度在0~0.1 rad之间,三种场景的角度差值接近实际角度(场景3实际角度为0.588 rad,场景1和场景2实际角度为0)。
由图10可知,随着移动时间增加,三个场景的移动节点位置估计值与实际值的误差如下: 场景1误差在1.4~2.8 m之间,场景2误差在0.1~1.2 m之间,场景3误差在0.8~1.9 m。测量坐标与实际坐标间的误差表现为场景1>场景3>场景2。这是由于场景1和场景3中反射波较多的缘故。
5 结论
本文提出一种基于室内信道传播特性跟踪定位算法,在密闭走廊、开放走廊和实验室三种不同场景下,对室内无线信号进行测试、统计和分析,并构建了室内信道传播模型。在实际测量过程中,根据信道模型和锚节点定期测试的RSSI数据,利用最大似然法实现对移动节点的跟踪定位,估算其速度、行进方向和坐标位置。软件仿真和实测结果证明,本文提出的方法可以在不同的无线信道条件下,满足室内定位和跟踪要求,可应用于仓库、超市等室内定位场景。

