基于区域合并的FCM图像分割改进算法

胡学刚，段 瑶，严思奇

(重庆邮电大学 通信与信息工程学院，重庆 400065)

1 引 言

图像分割是一种基本的计算机视觉技术，是从图像处理到图像分析的关键步骤[1].基于模糊C均值聚类的图像分割算法(FCM算法)[2]作为一种结合了模糊理论和聚类分析的分割算法，被广泛应用于图像分割[3-6].与活动轮廓模型、马尔可夫模型和水平集模型等算法相比，FCM算法应用于图像分割具有步骤简单、易于实现、执行效率高等特点[4]，但这种算法在聚类时未考虑图像的空间信息，其分割结果很容易受到图像中的噪声、异常点和纹理的影响[5，6].为了解决上述问题，研究者们主要通过在FCM算法的目标函数中增加约束项来提高抗噪能力[7-11].例如，Ahmed等人提出FCM_S算法[7]，通过在聚类的每次迭代中计算邻域像素的影响，提高了算法的抗噪性能.但每次迭代都需要计算邻域像素，明显提升了时间复杂度.蔡伟玲等人同时考虑局部区域像素间灰度关系和空间关系提出的快速广义的模糊C均值分割算法(FGFCM算法)[8]，首先根据像素间相似性生成一张和图像，然后对和图像的直方图进行聚类，其分割效果和效率都有明显的提升.公茂果等人提出的算法[9]在利用空间邻域信息的同时，引入核函数将原空间样本映射到高维特征空间后再进行聚类，使得原本线性不可分的样本变得近似线性可分，进一步提升了FCM算法的分割性能.Ma等人在FGFCM算法的框架下，提出一种基于非局部空间信息的FCM算法(NLFCM算法)[10]，该算法使用像素间结构相似性来定义空间约束项，然后将基于此得到的和图像引入FGFCM算法框架中求解，能得到更好的分割结果.Rajaby等人给出的分割方法[11]首先引入一种自适应权重，同时考虑色度和亮度来重构目标函数，提高了分割性能，但增加了计算复杂度.

由于图像各区域之间存在较多相似性，现有多数算法都容易产生过分割，得到不符合人视觉特性的分割结果.针对此问题，本文提出了一种基于区域合并的FCM图像分割算法.该算法使用FGFCM算法获得初始分割，然后给出一种合并策略对初始分割进行合并，得到最终的分割结果.所提出的算法解决了现有普遍存在的过分割问题，且有更好的分割效果.

2 FGFCM算法概述

在给定的图像中，令xi表示图像中第i个像素的灰度值，(pi，qi)表示xi的坐标，第i个像素与第j个像素的相似程度Sij表示为：

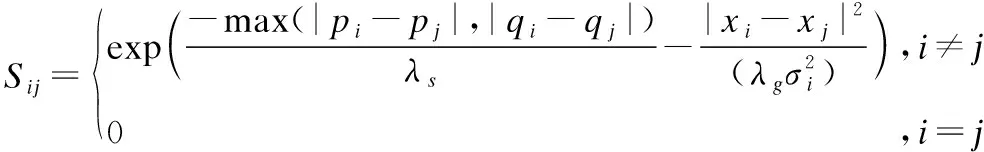
(1)

这里λs和λg分别是控制距离差异和灰度差异的尺度因子，λs通常取值为3，λg通常在0.5至6之间选择[8]，σi是一个反应局部区域平坦程度的值.

利用相似性度量值Sij创建和图像ξ.由公式(2)可以得到图像中第i个像素点的灰度值xi′：

(2)

ξ中第l个灰度级ξl的像素点个数为γl，由此可以得到FGFCM算法如下的目标函数Jm：

(3)

这里M是新图像ξ的灰度直方图中灰度级的总数，c是聚类个数，m为收敛常数，通常在1.5至2.5之间取值[12].ujl为第l个灰度级属于第j个类别的隶属度，vj表示第j个聚类中心的灰度值.

利用拉格朗日乘数法，迭代求式(3)的极小值，以获得最优解或局部最优解，由此得到聚类结果.即FGFCM算法的聚类中心与隶属度矩阵的迭代公式分别为式(4)与式(5).

(4)

(5)

3 本文算法

本文提出了一种基于区域合并的FCM图像分割算法.该算法首先使用FGFCM算法获得初始分割，然后利用区域间颜色信息、空间上的边缘和邻接关系建立带权重的区域邻接矩阵[13]，最后根据区域间的权重和区域面积大小合并满足条件的相邻区域，得到最终分割结果.合并的关键问题包括区域间距离度量和区域合并策略.

3.1 区域间距离度量

在区域合并技术中，区域间关系需要使用距离度量来量化表示.使用带权重的区域邻接矩阵来表示和存储区域间距离度量，其数学表达为如下的一个无向图G.

G=(V，E，W)

(6)

其中，V是图像中所有区域的集合(顶点集).E是图像中所有区域对之间边的集合(边集).W是图像中所有区域对之间边的权重的集合，一对区域之间边的权重是一个大于0的数，可由区域间特性计算得到.

区域合并时，两个区域间边的权重是合并的重要依据，定义两个区域Ri与Rj间边的权重为两个区域间距离度量Dij.若两个区域在空间上毗邻，颜色上相似，并且交接处没有明显的边缘存在，则将其合并.为此定义两个区域间距离度量Dij如下式(7):

(7)

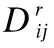
(8)

(9)

其中，μi和μj分别代表两个区域Ri和Rj的颜色均值，‖·‖表示欧氏距离.Eij和Eji分别表示位于相邻区域公共边缘两侧的像素点的集合，|Eij|和|Eji|分别代表Eij和Eji中像素的个数.xk和xl分别表示相邻两区域边缘两侧第k个点和第l个点的颜色值.Δij表示两个区域Ri和Rj的邻接关系，其定义如下.

(10)

建立一个带权重的v阶区域邻接矩阵，其第m行n列的值为第m个区域与第n个区域之间的距离，该矩阵主对角线上的值设为∞.

3.2 区域合并策略

在区域合并过程中，以何种顺序、在何种条件下进行区域合并决定了合并的效果.本文提出的区域合并策略包括基于区域间权重的合并顺序、基于区域间权重和区域面积的合并决策规则.

合并顺序以带权重的区域邻接矩阵为依据，首先取其主对角线右上方的值，排除两区域相互邻接计算两次的干扰.然后取出邻接矩阵中所有不为无穷大的数进行升序排序，合并顺序按权值从小到大进行，即先对距离较近的两个区域作处理.

考虑到区域间的相似关系，以及面积较小区域通常无实际意义的因素，我们使用区域间权重和区域面积来建立合并决策规则：当区域Ri和Rj间权重小于阈值T1或者两区域中任意一个面积小于阈值T2时，两区域合并.这里使用3.1节中的区域间距离度量，将阈值T1设为所有区域间距离度量的均值μD和方差σD之差，其定义由式(11)给出.

T1=μD-σD

(11)

阈值T2用于去除图像中面积过小的区域，根据图像的用途不同，由人工确定T2的值(本文统一设定为10).按顺序遍历所有相邻区域后，合并停止.

3.3 具体算法设计

综合上述思路，本文提出的分割算法步骤如下：

步骤1.使用FGFCM算法，得到初始分割结果；

步骤2.对初始分割结果进行区域标记，由区域间关系建立区域邻接矩阵[14]；

步骤3.计算邻接区域间距离度量，代入区域邻接矩阵中，得到带权重的区域邻接矩阵；

步骤4.计算权重阈值T1，设定面积阈值T2；

步骤5.根据合并规则合并相似区域，得到最终分割结果.

4 实验结果与分析

为了验证本文算法的有效性，本节首先对两幅图像使用FGFCM算法和本文算法进行了分割对比实验，然后选取两幅图像使用NLFCM算法和本文算法进行了分割对比实验，分割结果中每个区域的颜色以该区域的颜色均值来表示.实验平台为Win10操作系统，8GB内存，酷睿i5 6300HQ处理器(2.3GHz)，Matlab 2014b.FGFCM算法与NLFCM算法的参数选取与对应文献中参数一样，本文算法的阈值T2统一设定为10.在图1(a)、图1(d)、图2(a)和图2(d)所对应的实验中，根据图像中类别的多少，聚类数c的取值分别为3、3、4和5.

图1是使用FGFCM算法和本文算法得到的分割结果对比.其中，图1(a)是独狼图像的原图，图1(b)和图1(c)分别是FGFCM算法的分割结果和本文算法的分割结果.从实验结果可以看出，FGFCM算法分割结果没有将狼的身体分割为一个整体，在身体上出现空洞形式的过分割区域，而本文算法正确地将狼的身体分割成为了一个整体.在背景的分割上，本文算法倾向于把后面的黑色山体分割为一个整体，更符合人类主观视觉特点.

图1(d)是飞鸟图像的原图，图1(e)是FGFCM算法对图1(d)的分割结果，图1(f)是本文算法对图1(d)的分割结果.由原图可以看出，飞鸟的背景存在光照不均匀现象，FGFCM算法这种完全由聚类得到结果的分割方法不能将背景天空分割为一个整体，而本文算法经过区域间相似性对比，正确地合并了图1(f)中被过分割的天空背景，使其成为一个整体区域.

图1 合并前后的分割对比Fig.1 Comparison of the results before and after the merger

为了客观评价本文算法的分割性能，此处我们使用一种基于分割结果的评判标准：E指标[14].该指标基于分割结果的信息熵来评判分割效果，其值越小越好.E指标的定义如下：

E=Hl(I)+Hr(I)

(12)

其中，Hl(I)称为布局熵(layout entropy)，Hr(I)称为期望区域熵(expected region entropy).Hl(I)和Hr(I)的定义分别如式(13)和式(14)所示.

(13)

(14)

上面两式中，c是所有区域的数量，j表示分割出的第j个区域，I表示整个图像，Sj表示区域j的面积，SI表示整个图像的面积.H(Rj)表示第j个区域的期望区域熵，其定义为式(15).

(15)

式中Vj表示第j个区域内所有可能出现的灰度值集合(这里是0-255)，m是属于Vj的一个灰度值，Lj(m)表示第j个区域中，出现灰度值m的像素个数.

表1是对图1(a)和图1(d)对应实验E指标的比较.从表1可以看出，本文算法在每一个图中都得到了最优的客观指标数值，与主观观测结果一致，进一步说明本文算法有效.

表1 合并前后的E指标比较Table 1 Comparison of E indicators before and after merger

为了进一步说明本文算法的分割性能，我们使用本文算法与NLFCM算法对两幅图像做分割对比实验，实验结果如图2所示.

图2 与NLFCM算法分割对比表现Fig.2 Comparison of segmentation performance with NLFCM algorithm

图2(a)是教堂图像的原图，图2(b)是NLFCM算法对图2(a)的分割结果，图2(c)是本文算法对图2(a)的分割结果.由原图可以看出，教堂图像的天空存在光照不均匀现象，房顶也有由反光导致的光照变化，NLFCM算法将天空和房顶错误地过分割为几个区域，而本文算法正确地分割出了房顶与天空，将它们视为一个整体区域.

分别用NLFCM算法和本文算法对大象图像图2(d)作分割，得到图2(e)和图2(f)，可以看出，NLFCM算法不能应对天空和草地的缓慢颜色变化，把天空和草地都分割成了多个区域，与人类的视觉特性不相符，存在过分割，而本文算法成功地消除了这些过分割，将天空和地面分为一个整体区域，得到了满意的分割结果.

表2 合并前后的E指标比较Table 2 Comparison of E indicators before and after merger

表2是对图2(a)和图2(d)对应实验E指标的比较.可以看出，本文算法的客观指标在每一个图中都有最小的数值，说明分割效果较好，与主观观测结果一致，进一步说明本文算法的有效性.

5 结束语

本文针对现有FCM算法容易产生过分割的问题，提出一种结合FCM聚类分割和区域合并的图像分割算法.实验表明，该算法能有效克服现有FCM算法容易产生过分割的缺点，得到更优的主观感受和客观指标，比现有算法有更好的分割性能.