稀疏自动编码器在多维电能计量误差预测中的应用

张乐平，罗鸿轩，胡珊珊，王 吉，寇子超

(1．南方电网科学研究院有限责任公司，广东 广州 510080;2．武汉大学动力与机械学院，湖北 武汉 430072)

0 引言

电能计量标准器的各级检定试验都是在设定参比条件的试验室内进行的［1］。现场工况复杂，且往往受到多因素影响。随着电力系统检定需求的进一步提升，以满足现场检验、校验需求的各种标准和应用应运而生，对多维条件下相关器具准确度的研究需求也相应提升［2］。电能计量标准器具在多维条件下的准确度变化，主要是由于运行条件所带来的附加误差变化。针对这种附加误差变化的研究，本质上是一个多元非线性复杂系统的回归和预测问题［3-6］。

深度学习作为目前机器学习领域颇受关注的方法，具有强大的非线性拟合性能。其一方面在人工智能与机器学习领域得到了充分的研究［7-9］;另一方面与电力系统相关问题的结合逐渐受到学界的重视，尤其是在负荷预测、光伏及风能历史数据分析［10-14］等领域。但机器学习技术在计量领域的应用仍十分有限。

自动编码器是一种采用无监督预训练，将数据降维的深度学习模型［15］。本文采用自动编码器作为深度学习的基本模块，采用无监督预训练优化网络初始权值，再采用有监督微调方法完成训练过程;提出一种稀疏化的训练方法，并在实际运行环境下采用数据集进行训练，验证了该模型的准确性和有效性。

1 电能计量标准器溯源与计量特性

1．1 电能计量标准器的溯源方法

电能标准器是在电能计量装置的溯源路径中，处于标准计量器具一级的电能计量设备。在我国，工频电能计量基准及其量值传递系统的溯源依据JJG 2074-2007《交流电能计量器具检定系统表》。

电能表计量器具的计量可以逐级向上溯源，直至国家计量副基准。一般现场校验仪和标准表等计量标准器的精度要求为0．05级，而关口电能表的精度要求为0．2S 或0．5S级。

由此可见，电能计量标准器处于电能计量设备的溯源路径中的关键位置，直接影响各用电单位和关口的电能计量设备检定与校验。因此，电能计量标准器的准确度检定工作，在电力计量中具有十分重要的地位。

1．2 多维条件下电能标准器的计量特性

由于对电能计量标准器计量产生影响的因素非常多样，并且具有较大的非线性和不确定性，本文采用控制变量法，对精度为0．05级的标准设备进行影响量试验。试验采用3种来自不同生产厂家的标准表，溯源标准器具精度为0．01级。试验项目包括电流、电压、功率因数、频率、环境温湿度及谐波等。

对试验数据分别进行Pearson、Spearman和Kendall相关性分析。影响因素相关性分析结果如表1所示。

由表1可知，电压、电流和温度对附加误差的影响均较大。温度对附加误差的影响呈现分段特性。在20℃以下，温度和误差呈非线性负相关，Spearman相关系数为－0．338，通过显著性检验;在20℃以上，则呈非线性正相关。而湿度对附加误差的影响则较小。

表1 影响因素相关性分析结果Tab．1 Correlation analysis results of influencing factors

2 稀疏自动编码器的深度训练方法

2．1 稀疏自动编码器

稀疏自动编码器网络结构如图1所示。

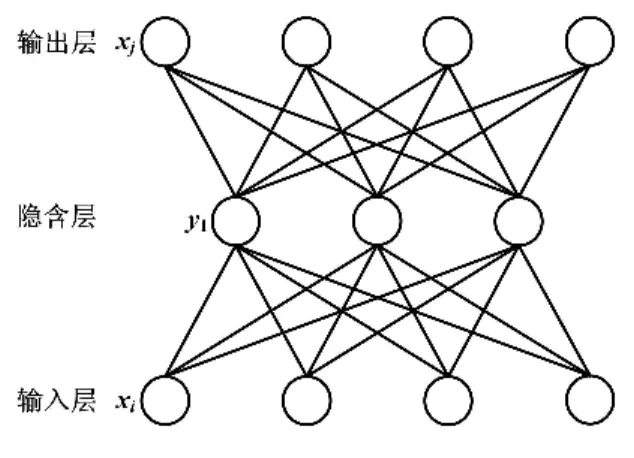
图1 稀疏自动编码器网络结构图Fig．1 Network structure of sparse automatic encoder

稀疏自动编码器是神经网络的一种，其机制是在无监督过程下使其输出与输入近似。稀疏自动编码器的基本模型是一个三层网络，其隐含层神经元个数往往少于输入特征数，因此输入层到隐含层相当于一个编码过程，而隐含层到输出层则视为解码。在编码过程中，自动编码器试图将输入向量x按一定的映射编码为xen。

输入层到隐含层的映射即编码过程，从隐含层到输入层的过程，自动编码器对该向量的对应低维向量y进行“解码”，得到与x同维度向量x'。通过反向传播算法训练网络，并调整f(x)与g(x)的参数以最小化重构误差，以得到一个足够小的正数ζ，且|x'－x|＜ξ。

稀疏自动编码器算法逻辑如图2所示。

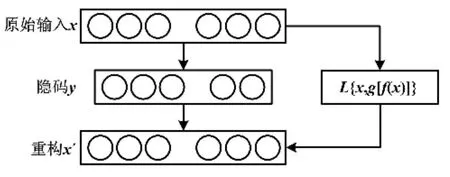
图2 稀疏自动编码器算法逻辑图Fig．2 Algorithm logic of sparse automatic encoder

本文将电能计量器具的运行条件矩阵X作为自动编码器的输入矩阵，xi∈Rn×1是矩阵X中的第i条测试数据对应的条件向量。将xi作为自动编码器的第i个输入向量，编码层的神经元数量为 d，通过式 (1)得到编码 hi∈ Rd×1。

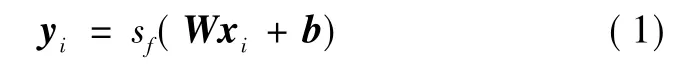
式中:sf为编码器的激活函数，一般采用sigmoid函数或ReLU 函数;W∈id×n为权值矩阵;b∈id×1为偏置向量。

将yi输入解码层，通过式(2)重构输入向量，获得

式中:sg为解码器的激活函数。

权值矩阵一般被限制为W=WT，b'则是解码层的偏置向量。

训练过程中，自动编码器通过不断调整解码层和编码层的权值矩阵和偏置向量这4个参数，即调整θ=以最小化重构误差。

为自动编码器加入基于Kullback-Leibler(KL)散度的稀疏性限制，从而在训模型练过程中尽量避免过拟合。其限制如式(4)所示。

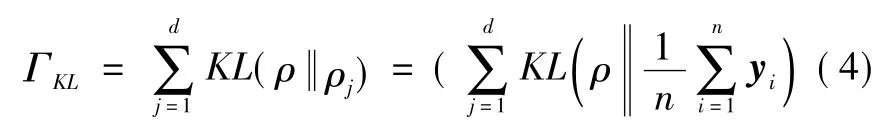
式中:ρj为隐含层的平均活跃度:KL(ρ‖ρj)表示分别以ρ和ρj为均值的2个变量之间的相对熵。

本文构建的自动编码器重构误差的损失函数(loss function)可归纳为:

式中:α为控制稀疏限制的权重因子。

2．2 网络结构

通过使用同样数据集，对最小二乘支持向量机(least-square support vectormachine，LS-SVM)、全连接多层感知机(fully-connected perceptions，FCP)和采用本文方法的深度训练自编码器(stacked sparse autoencoder，SSA)进行试验，并观察其训练效果。FCP和SSA网络结构对比如图3所示。

FCP网络有4个隐含层，每个隐含层含有5个感知机单元，层与层之间的感知机单元采用全连接方式。SSA网络共有4个自动编码器，编码器所含单元数分别为6、5、4、3，每2层采用无监督预训练编码器输入与输出，并将上一层编码器的中间层作为下一层编码器的输入;输出层为全连接层。在训练时，将样本数据的作为预训练集、其余作为微调训练集。

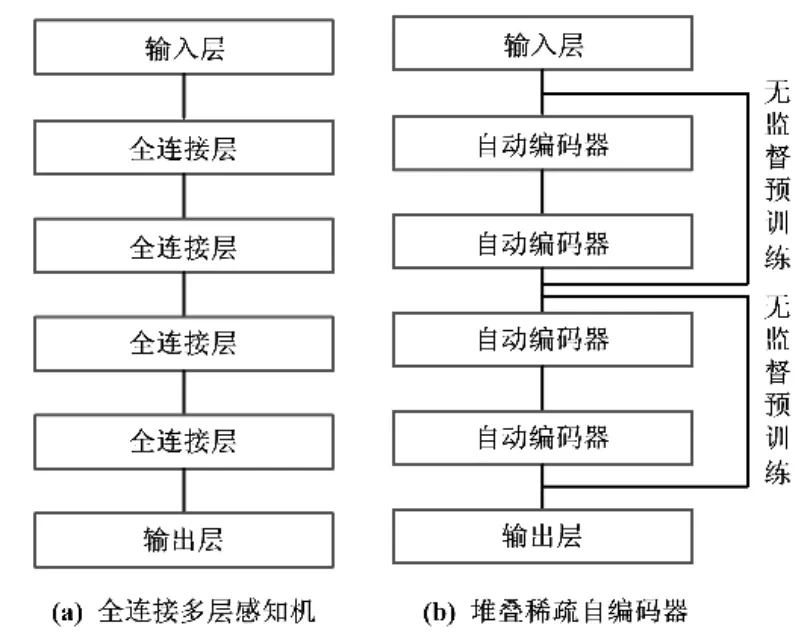
图3 网络结构对比图Fig．3 Comparison of network structures

设训练学习率η=0．001，采用随机梯度下降法进行训练，batchsize=50。损失函数采用均方误差(mean squared error，MSE):

对于给定样例集合 D={(x1，y1)，(x2，y2)，…，(xm，ym)}，xi∈Rd，yi∈Rd。其中:yi为示例 xi的真实标记;m为样本数据量;f(x)为学习器预测结果。

3 标准器检定试验

3．1 试验数据

试验选取国内外数家不同厂商生产的电能计量标准表和标准器，准确度均为0．05级。对其在电流、电压、功率因数、频率、环境温度、湿度与谐波各条件变化情况下的计量准确度及误差进行试验，并记录相关数据。因此，预测模型包括7个输入变量和1个输出量，分别对应7个条件因素和计量误差。总数据集包括1 710个样本。

3．2 网络参数选择试验

神经网络模型除了待调整的网络权值和偏置参数以外，还拥有其他各项超参数。超参数的选取会对网络模型的训练结果产生至关重要的影响。为使网络参数达到一个较佳的状态，应尽量减小训练结果的误差。

首先，对神经网络的超参数的选取进行对比试验。图4所示为迭代20 000次时，采用不同激活函数的网络模型训练结果。

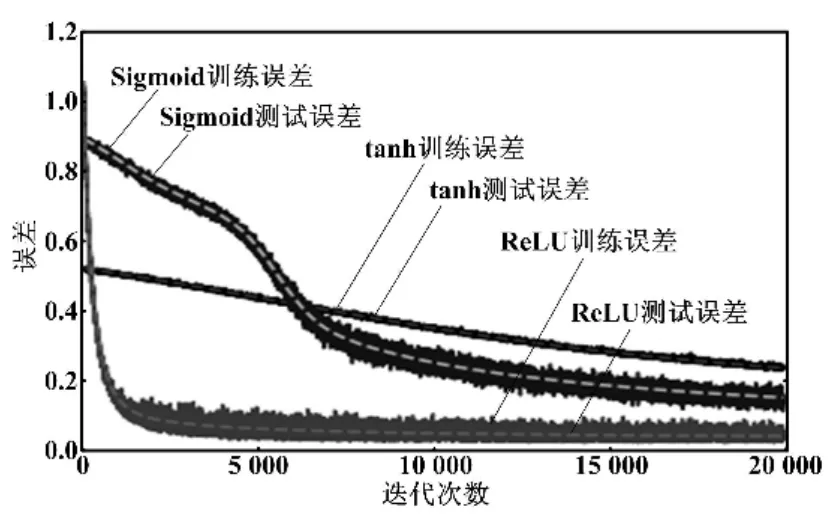
图4 激活函数对比图Fig．4 Comparison of activation functions

由图4可以看出，当采用ReLU函数时，网络模型的训练和测试误差下降最快，收敛效果好，最终误差也最小。因此，激活函数采用ReLU函数。该函数在多层感知机训练试验中的收敛速度和误差反馈效果都有良好的表现。

图5所示为迭代3 000次时，当网络含有不同数量隐含层时的网络模型训练结果。

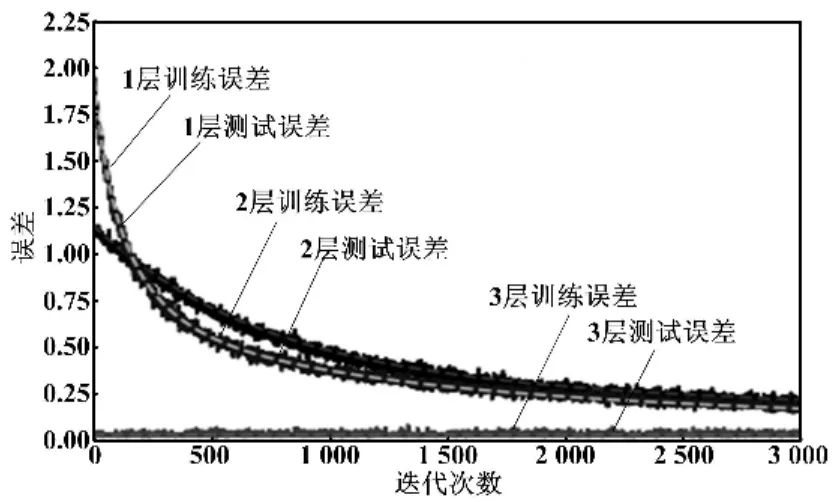
图5 隐含层数对比图Fig．5 Comparison of implication layer

从图5中可以看出，当隐含层数量为3层时，网络的收敛速度非常快，几乎在一开始就达到了非常好的迭代效果，最终误差最小，且预测数据的整体方差也比较小。

3．3 网络模型对比试验

对同样的样本数据，分别采用LS-SVM、FCP、SSA进行试验。其训练效果对比如图6所示。

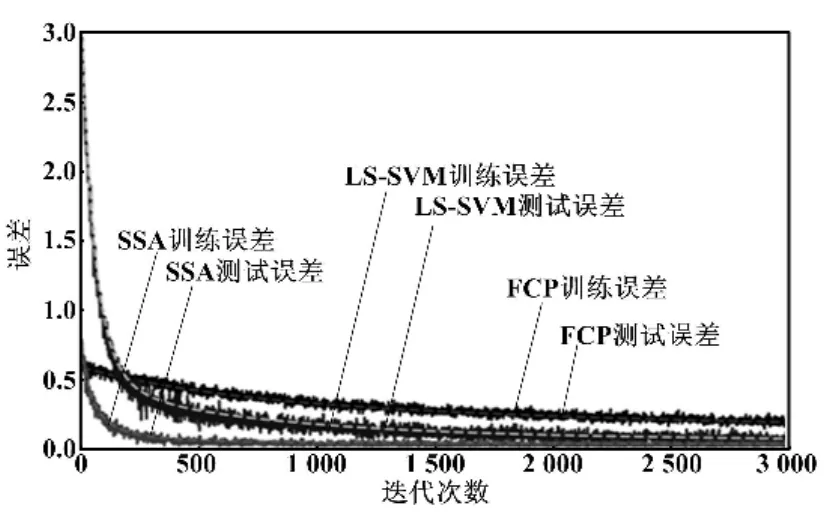
图6 训练效果对比图Fig．6 Comparison of training effects

从图6可以看出，LS-SVM在最初几次迭代中，效果优于FCP和SSA模型。这是由于SVM在针对小样本空间的学习能力优于神经网络算法。但随着训练样本和迭代次数的增加，神经网络的学习潜力开始展现，最终FCP和SSA的模型误差都要小于LS-SVM。由此证明，在样本数量足够的情况下，神经网络算法对大数据的适应能力更强。此外，SSA模型学习的收敛速度更快，最终误差更小。由试验可知，LS-SVM的MSE为99．63，FCP 的 MSE 为99．84%，SSA 的 MSE 为 99．92。因此，SSA模型针对多维条件下电能计量标准器的误差预测性能更优。

4 结束语

随着电力系统技术的发展、新型电力电子设备的投入，对电力系统的计量要求也随之提高。同时，针对传统计量检定技术模式的便携性改进在电力生产过程中也有非常大的实际需求。

本文针对非参比条件下的复杂环境和多维条件产生的附加误差，研究了电能计量标准器的准确度变化规律，并将其抽象为一个非线性预测问题。通过深度挖掘常见维度对附加误差的影响数据，提出了基于堆叠降噪自动编码器网络的多维条件下电能计量标准器准确度和附加误差预测SSA模型。通过系统验证，分析并优选学习模型的结构参数;对不同模型进行性能预测，并利用试验数据分析了SSA模型的预测情况，证明了该模型的良好精度。