级间耦合刚度对行星传动系统灵敏度的影响分析*

李剑英，朱天军，宗长富，蔡超明，胡青春

(1. 肇庆学院 机械与汽车工程学院，广东 肇庆 526061; 2. 华南理工大学 机械与汽车工程学院，广东 广州 510640)

0 引 言

为解决新能源汽车多动力源耦合问题，常采用行星传动机构作为其传动系统的关键零部件[1-2]，有学者指出，若机构中的内齿圈采用薄壁结构，其弹性对传动系统动态特性的影响在某些特定场合应被计及[3-6]，在传动过程中发生的显著变形将对系统的动态特性有重要影响，因此在建立动力学模型时不再视内齿圈为刚体. 国内外学者在这方面也进行了初步探讨，如WU和 PARKER[7-9]采用摄动和模态分析方法，研究了均布/非均布行星传动的模态特性，并分析了弹性内齿圈行星传动的参数化不稳定性. 张俊等[10-11]指出内齿圈的柔性对传动系统的振动特性存在一定影响. 然而，上述文献主要针对的是单级行星传动，针对计入内齿圈弹性的两级行星传动动力学方面，Li等[12-16]进行了研究. 行星传动的动态性能会受到系统参数影响，而弹性支承薄壁内齿圈两级行星传动系统又涉及到众多参数，如构件的质量、转动惯量、支承刚度及啮合副的啮合刚度和内齿圈的弯曲刚度等，通过对这些参数的灵敏度分析，进而了解它们对系统固有频率的影响规律，可用来指导选择系统参数来降低构件质量，优化载荷分配和避免共振发生等. 另外，通过了解系统参数对模态能量的影响趋势，来降低行星传动的振动强度.

Lin和Parker[17]基于平移-扭转模型[18]研究了系统参数对行星传动固有频率灵敏度的影响，而文献[17]针对的是单级行星传动. Guo和 Parker[19]基于复合行星齿轮传动系统的平移-扭转模型[18]研究了系统参数对固有频率灵敏度的影响. 齐寅明[20]则以啮合刚度为例分析了盾构机刀盘驱动三级串联行星齿轮传动系统固有频率的灵敏度. 赵永强[21]研究了两级人字齿混合行星齿轮系统的啮合刚度和级间扭转刚度对固有频率敏感度的影响. 在上述文献所建立的动力学模型中，均将轮系中各构件视为刚体来研究其固有频率的灵敏度，而对计入内齿圈弹性的两级行星传动固有频率灵敏度的研究还未见报道. 本文采用有限差分法并结合模态能量研究了级间耦合刚度参数变化对弹性支承薄壁内齿圈两级行星传动系统固有频率的影响，为行星传动系统参数选择提供理论依据，以达到行星传动所要求的动态性能.

1 弹性支承薄壁内齿圈两级行星传动系统动力学模型

1.1 建模假设

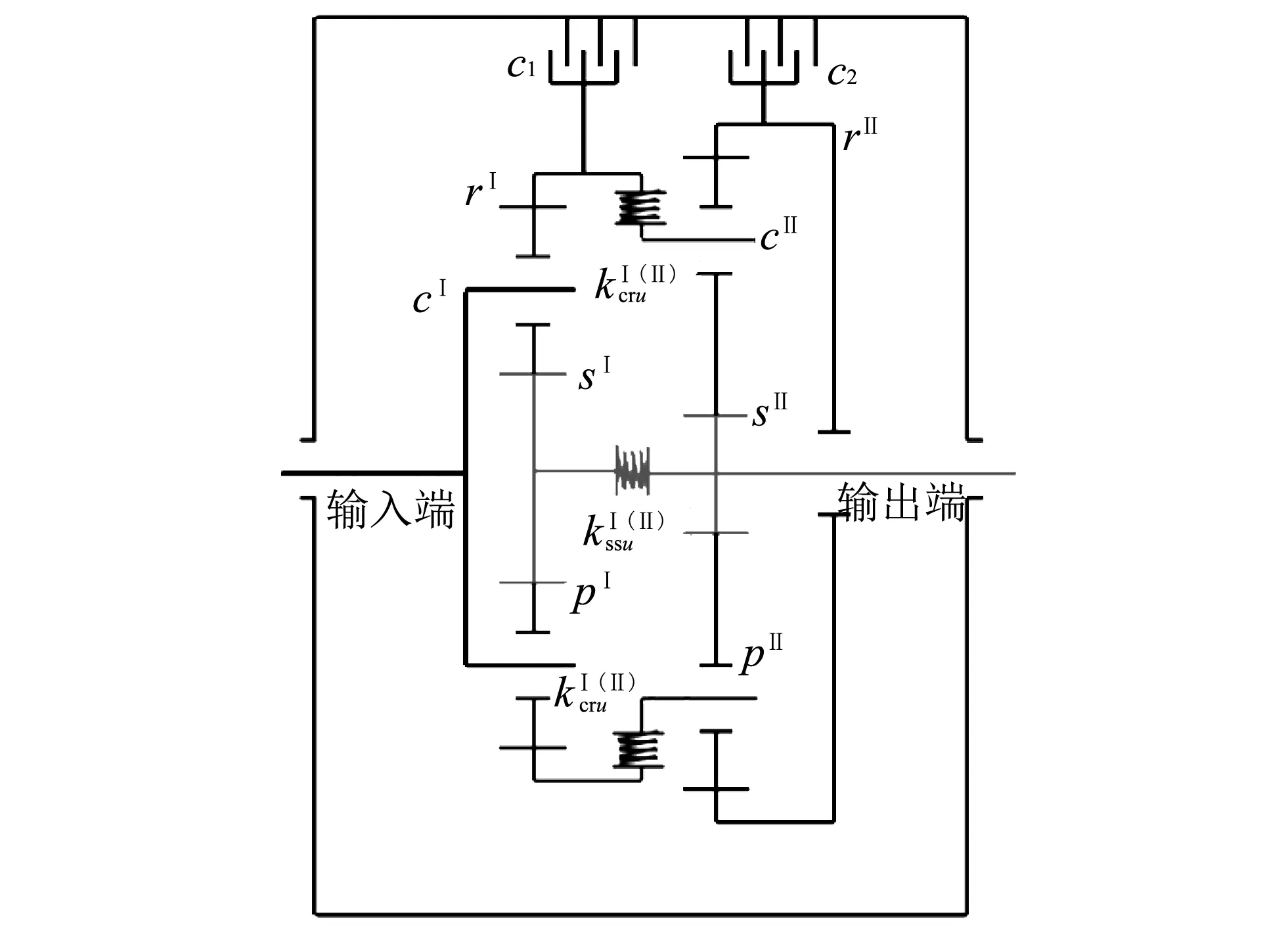
图 1 弹性支承薄壁内齿圈两级行星传动机构简图Fig.1 Diagram of two-stage planetary transmission system with thin-walled ring gear on elastic supports

在动力学建模中做如下假设[12-14]：

1) 内齿圈视为薄弹性圆环，且在面内不能延展振动，太阳轮、行星轮和行星架均视为刚体，设定各行星轮均布安装且质量、尺寸、转动惯量等均相同.

2) 太阳轮、行星轮和行星架的支承刚度均为线刚度，而内齿圈的支承视为切向和径向刚度约束的弹性基.

3) 各齿轮副的啮合刚度取一个啮合周期内综合啮合刚度均值，计入系统各构件的扭转支承刚度； 忽略系统的阻尼、摩擦、传递误差等.

1.2 计算模型

图 2 弹性支承薄壁内齿圈两级行星传动系统动力学模型[12-14]Fig.2 Dynamic model of two-stage planetary transmission system with thin-walled ring gear on elastic supports

依据牛顿第二定律建立弹性支承薄壁内齿圈两级行星传动系统的运动微分方程[15-16]

(1)

(2)

(3)

(4)

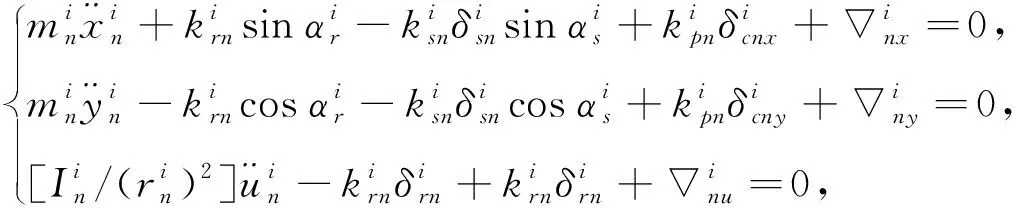
(5)

2 弹性支承薄壁内齿圈两级行星传动系统模态应变能及特征灵敏度计算

2.1 弹性支承薄壁内齿圈两级行星传动系统模态应变能

弹性支承薄壁内齿圈两级行星传动系统第i阶模态应变能可写成

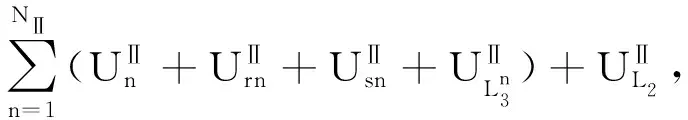
(6)

(7)

2.2 特征灵敏度计算

(8)

3 算 例

本文分析弹性支承薄壁内齿圈两级行星传动系统固有频率对级间耦合刚度参数的灵敏度，系统基本参数如表 1 所示[12-15]，第Ⅰ级和第Ⅱ级的行星轮个数均为4.

表 1 弹性支承薄壁内齿圈两级行星传动系统基本参数Tab.1 Parameters of two-stage planetary transmission system with thin-walled ring gear on elastic supports

3.1 第Ⅰ级内齿圈与第Ⅱ级行星架耦合刚度参数灵敏度

图 3 级间耦合刚度对系统固有频率的影响Fig.3 Influences of inter-stage coupling torsional stiffnesson

图 3 中标示的Ⅰ～Ⅲ情况分别定义如下：

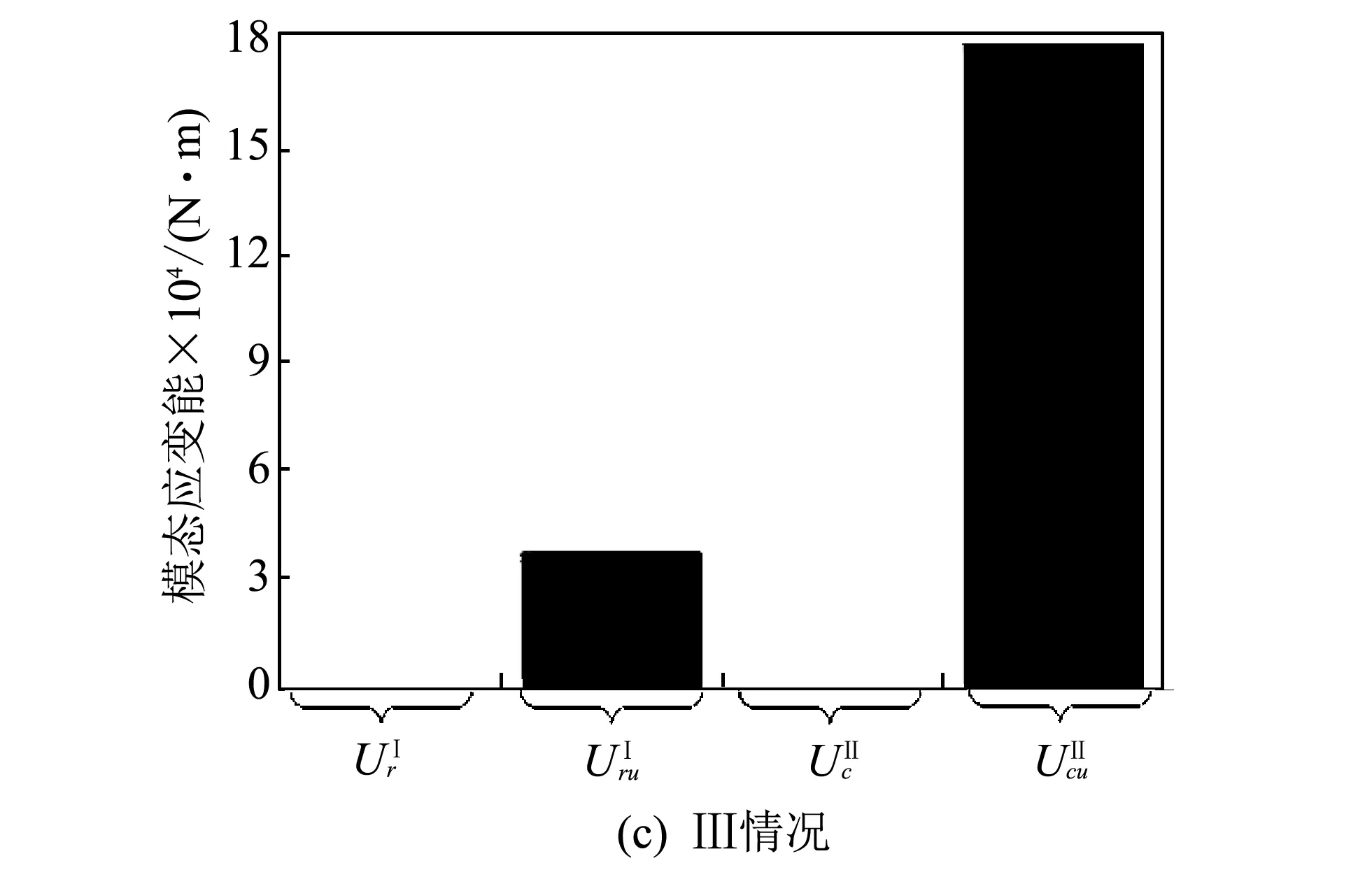
图 4 Ⅰ/Ⅱ级耦合扭转振动模式下各行星轮应变能分布图Fig.4 Strain energy distribution ofⅠ/Ⅱ stage coupling rotational mode

3.2 第Ⅰ级太阳轮与第Ⅱ级太阳轮耦合刚度参数灵敏度

图 5 中标示的Ⅰ～Ⅲ情况分别定义如下：

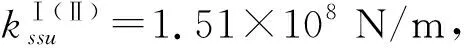
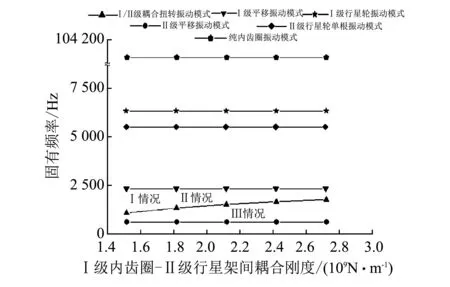
图 5 级间耦合刚度对系统固有频率的影响Fig.5 Influences of inter-stage coupling torsional stiffnesson natural frequencies

图 6 Ⅰ/Ⅱ级耦合扭转振动模式下各行星轮应变能分布图Fig.6 Strain energy distribution ofⅠ/Ⅱ stage coupling rotational mode

4 结 论

将第Ⅱ级内齿圈视为弹性连续体，其弹性支承结构简化为切向和径向刚度约束的弹性基，通过级间耦合的方法得到了某混合动力系统中两级行星齿轮机构的刚柔耦合混合动力学模型，基于所建模型，采用有限差分法并结合模态能量研究了四行星轮传动系统的固有频率对级间耦合刚度的灵敏度，研究结果表明：

1) 随第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度、第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度变化，Ⅰ/Ⅱ级耦合扭转振动模式的固有频率发生变化，其他各振动模式的固有频率均不变.

2) 随第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度、第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，Ⅰ/Ⅱ级耦合扭转振动模式的固有频率灵敏度程度减小.

3) 通过对Ⅰ/Ⅱ级耦合扭转振动模式下各行星轮应变能分析，验证了上述结论.