参数化单元边界元法解势流速度场问题

刘梦超 ，刘延俊 ，，薛钢 ，吴瀚崚

1山东大学海洋研究院，山东济南250100

2山东大学机械工程学院，山东济南250061

3山东大学高效清洁机械制造教育部重点实验室，山东济南250061

0 引 言

在势流理论下，海洋工程中的许多问题都可以归结为边界值问题，如波浪能发电装置、海洋石油钻井平台，以及船舶与波浪、水流的相互作用等。在现有的求解方法中：采用解析法求解精确、计算速度快，但对求解域的几何形状要求较为苛刻，只适用于一些几何形状较为简单的规则求解域，比如特征函数匹配展开法适用于截面为矩形的浮体与波浪的相互作用［1］，多极子法适用于截面为圆形的浮体与波浪的作用［2］；数值方法中的有限元法可以对复杂形状进行求解，但需要对整个求解域进行离散，计算量较大［3-4］。

相比于需要对整个求解域进行离散的方法，如有限元法、有限差分法等，边界元法具有显著的优势［5］。边界元法最显著的特点之一是在计算时更小的计算量和数据存储；此外，边界元法的数值精度通常要优于有限元法。采用边界元法仅需在求解域边界上进行离散，将三维问题转化为二维问题，二维问题转化为一维问题，即能很方便地处理无限域问题，这也是边界元法在水动力学问题中能得到广泛应用的原因之一［6］。

本文将分别采用二维下的非连续参数化单元和参数化单元边界元法解势流速度场问题，以便在较低的单元数下得到较为理想的求解精度，并采用一种三维下的参数化单元边界元法解势流速度场问题，以便快速得到可以接受的平均误差精度。

1 数学模型及积分方程建立

1.1 数学模型

势流问题中的流体为无旋、无粘性、不可压缩的理想流体，流场域满足拉普拉斯方程：

流场域满足相应的边界条件如下：

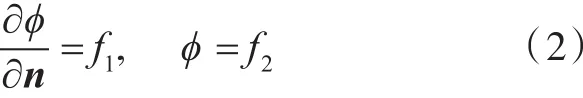
式中：n为物面某点的法向向量，垂直于物面向外；ϕ为速度势；f为给定的函数，下标1，2表示不同的给定函数（以下同）。

式（2）中的法向导数由式（3）定义：

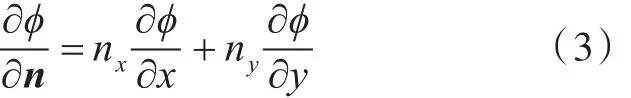
式中，nx，ny分别为物面单位法向向量在x，y轴上的分量，法向量方向垂直物面向外。需注意的是，单位法向量在不同的分量上是不同的，其是关于x和y的函数。求解域的控制方程（1）和边界条件已知，便构成了边界值问题，且存在特解。

1.2 积分方程的建立与离散

控制方程［7］存在基本解：

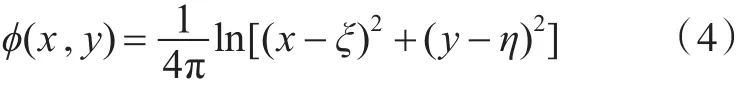
式中，ξ和η为选定点的坐标。根据格林公式，容易得边界积分方程

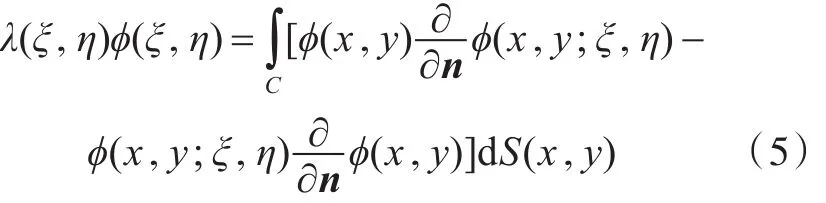
式中：S为曲线积分；C为积分路径。

在边界积分方程中，λ(ξ，η)的定义如下［8］：

将求解域的边界L使用非连续参数化单元近似为L1+L2+…+LN，各离散单元以逆时针顺序排列于求解域的边界上。离散单元L1，L2，…，LN由求解域边界上的点 (x1，y1)，(x2，y2)，…，(xN，yN)分隔，且N为有限值。各离散单元的边界条件由式（2），得

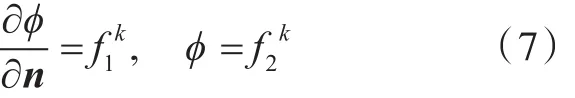
每个单元的端点坐标分别是(xk，yk)和(xk+1，yk+1)，且需注意，此处的 (xN+1，yN+1)=(x1，y1)。

贯穿整个非连续参数化单元，采用单元上点的f取值来近似fk。为了进行线性近似，需要在单元上的2个不同点取fk的近似值。这里选取 2 个 点 (ξk，ηk) 和 (ξN+k，ηN+k) ，它 们 与 点(xk，yk)，(xk+1，yk+1)之间的长度均为τlk。其中，lk为单元k的长度，τ为一给定系数（0＜τ＜1/2）。单元k的具体结构参见图1。

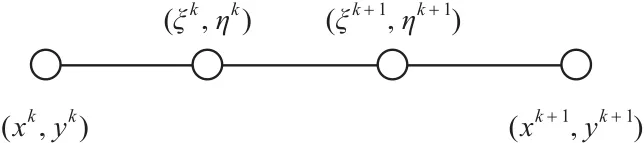
图1 非连续参数化单元示意图Fig.1 Schematic diagram of discontinuous parameterized element

点 (ξk，ηk)，(ξN+k，ηN+k)处的ϕ值分别由ϕk和ϕN+k指代。根据 Ang［9］的研究，为了用ϕk和ϕN+k近似表示出单元上ϕ值的线性变化，定义如下：

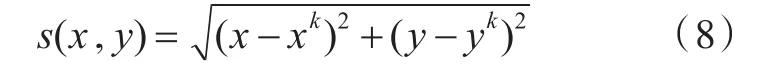
其中，(x，y)属于Lk（Lk为第k个离散单元）。由式（8）可知，s(x，y)为Lk上的点 (x，y)与端点 (xk，yk)间 的 距 离 。 注 意 ，点 (ξk，ηk) ，(ξN+K，ηN+k) 的s(x，y)值分别为τlk和 (1-τ)lk。所需ϕ(x，y)值的线性近似可以以ϕk，ϕN+k的形式给出，见式（9）。类似地，有，见式（10）。

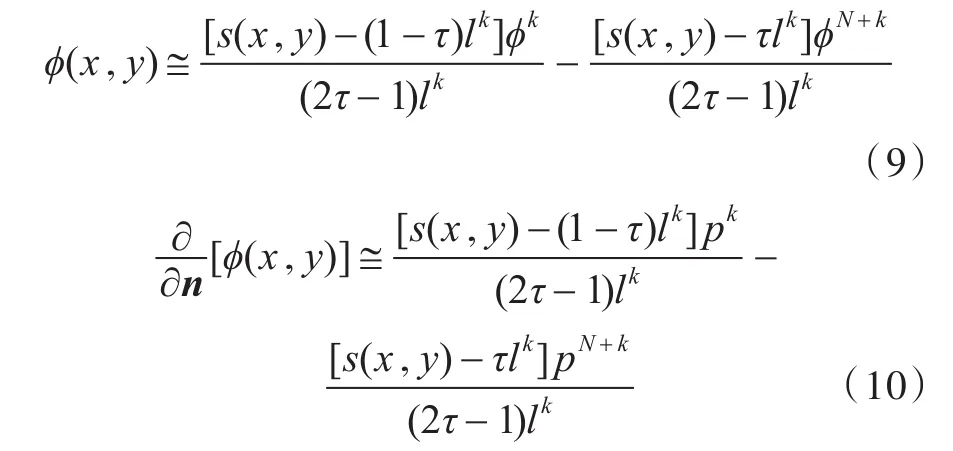
当 0＜τ＜1/2时，近似表达式（9）、式（10）定义为非连续单元。在对求解域边界L进行离散时，任意元素都有ϕk和pk，且其中有且仅有一个已知，如边界上ϕk已知，pk则未知。因此，式（9）、式（10）中有 2N个未知项。将式（9）和式（10）代入式（5），可得

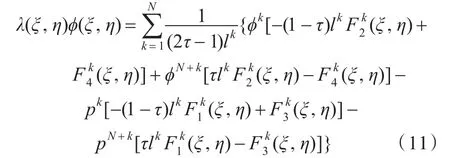
其中，

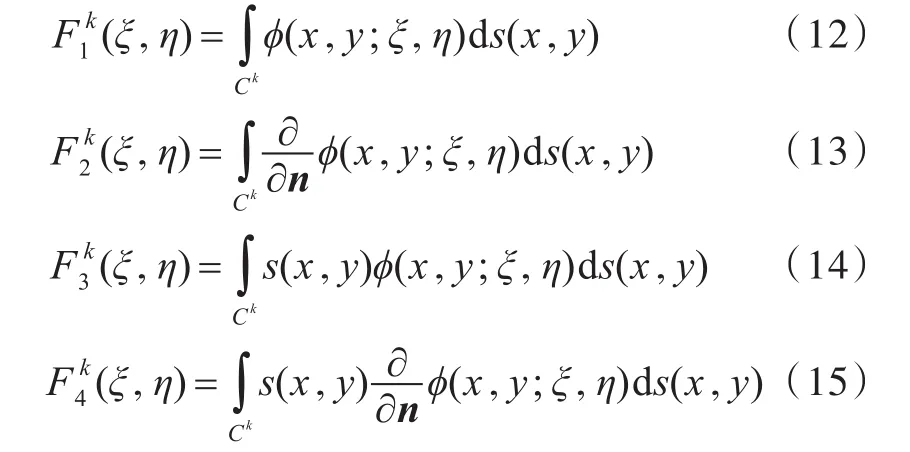
式中，Ck为单元积分路径。

为了求解式（11）右侧的2N个未知项，建立了一个2N阶线性代数方程组，即可以依次取点(ξ，η)为 (ξm，ηm)，其中m=1，2，…，2N，则又有式（16）。由图 1，可知点 (ξk，ηk)和 (ξN+k，ηN+k)为单元内的两点，则λ(ξm，ηm)=1/2，m=1，2，…，2N。式（16）又可写为式（17），式中的zk，zN+k表示元素上的未知量。其中在边界单元上，当ϕk已知时，amk，am(N+k)，bmk分别由式（18）、式（19）和式（20）给出，δmk为Kronecker数。在边界单元上，当pk已知时，情况与上述类似，此处不再赘述。(其中p=1，2，3，4)系数的参数化计算方法参见文献［9］。

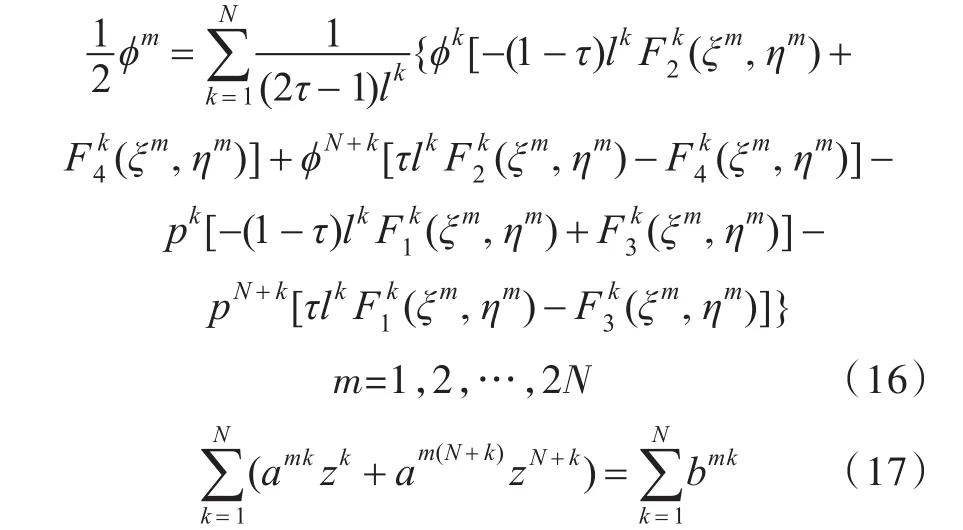
其中，

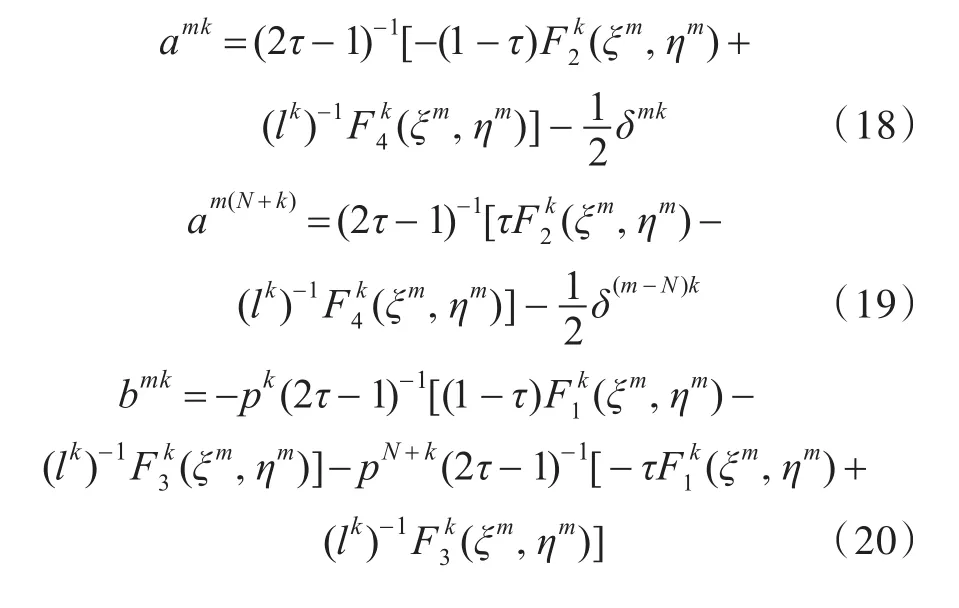
2 二维势流问题算例

2.1 矩形势流场算例

第1个算例，考虑矩形势流场问题，定解问题如下：

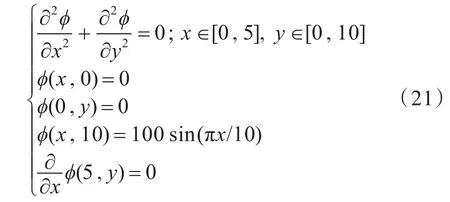
由文献［10］可知，上述问题的解析解为

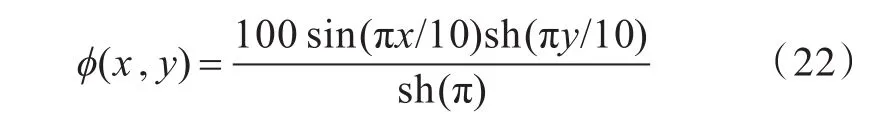
如图2所示，在分析计算中，将矩形计算域边界离散为30个单元，将边界积分方程离散，可以得到一个线性方程组，解此方程组即可求得所需的速度势或其他未知量。

图2 矩形流场示意图Fig.2 Schematic diagram of square flow field

在划分30个单元、采用非连续参数化单元离散的情况下，速度势的最大相对误差为0.63%，平均相对误差为0.19%，具体计算结果如表1所示；在划分单元数加倍、采用连续常数单元的情况下，速度势的最大相对误差为70.86%，平均相对误差为8.42%，计算结果如表2所示。

2.2 圆形势流场算例

第2个算例，考虑圆形势流场问题，定解问题如下：

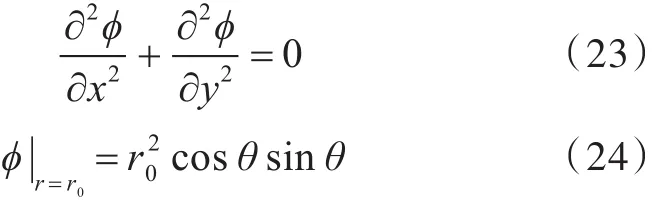
式中:r，θ为极坐标中的变量；r0为圆形流场域的半径，此处r0=1。其解析解为：

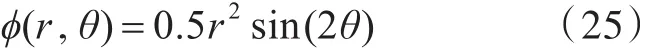
如图3所示，在分析计算中，将圆形计算域边界离散为32个单元，将边界积分方程离散，亦可得到一个线性方程组，解此方程组即可求得所需的速度势或其他未知量。

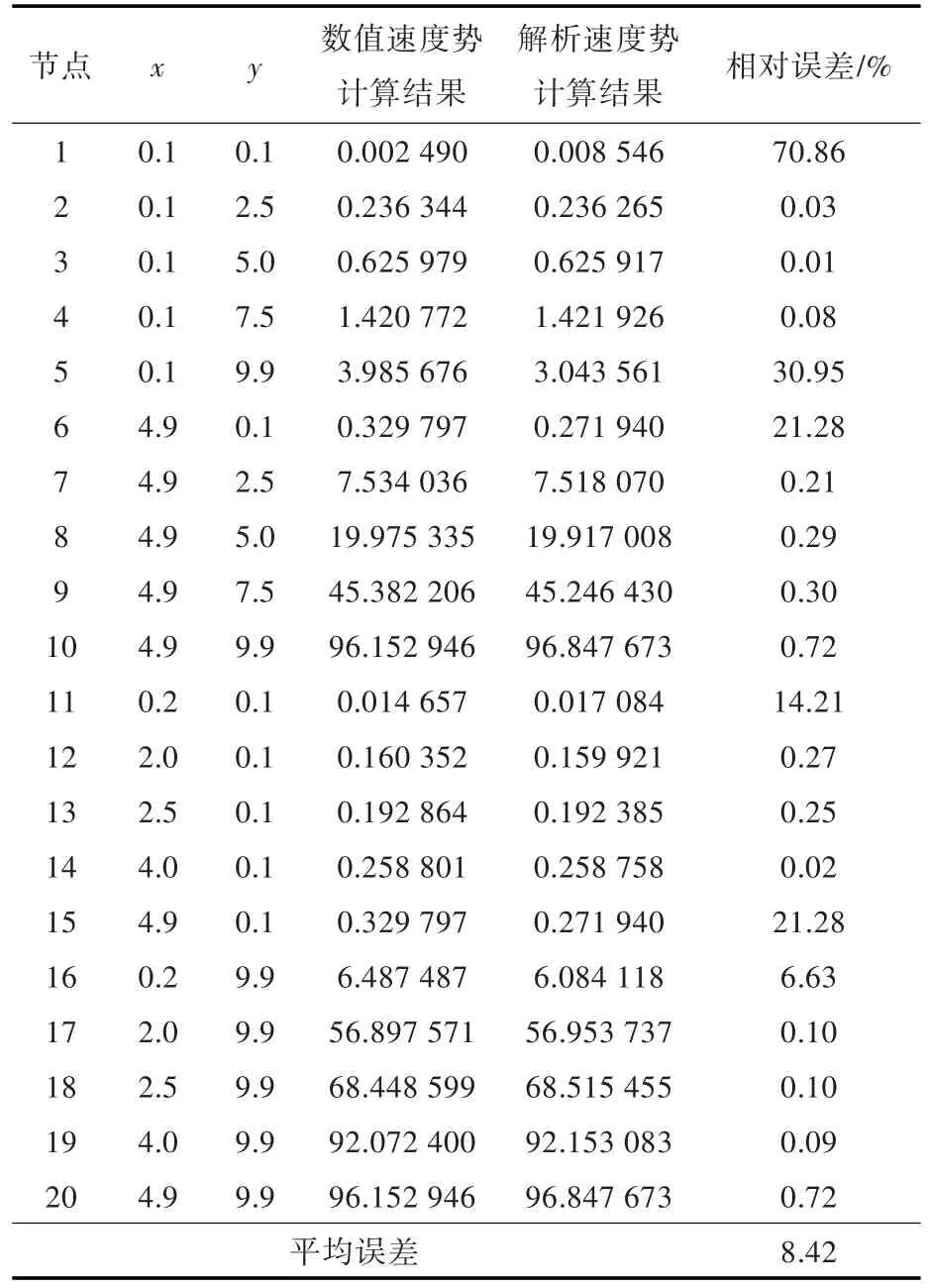
表2 参数化单元速度势计算结果（案例1）Table 2 The calculation results of velocity potential by parameterized elements（case 1）

在划分32个单元、采用非连续参数化单元离散的情况下，速度势的最大相对误差为0.02%，平均相对误差为0.01%，计算结果如表3所示；在划分单元数加倍、采用连续常数单元的情况下，速度势的最大相对误差为0.97%，平均相对误差为0.08%，计算结果如表4所示。

图3 圆形流场示意图Fig.3 Schematic diagram of circle flow field

2.3 非连续参数化单元与参数化单元比较

在二维情况下，分别采用非连续参数化单元和参数化单元边界元法解势流速度场问题，其中非连续参数化单元可以在较低的单元数下得到较为理想的求解精度。

由于非连续参数化单元上的物理量并非与单元节点处近似，故相比于参数化单元边界元法，非连续参数化单元在求解多边界问题时不但具有常数单元交界点无需特殊处理的优点，而且还具有线性及高次单元在较少单元数下得到较高求解精度的特点。

当采用传统常数或线性单元的直接边界元法解势流速度场问题时，除了边界近似带来的误差，还有在求矩阵系数时由高斯积分法近似引起的误差。非连续参数化单元由于是将单元上的点进行参数化，求解系数时使用解析表达式求解，即柯西主值积分，故其只有边界近似误差以及系统矩阵求解时带来的误差。

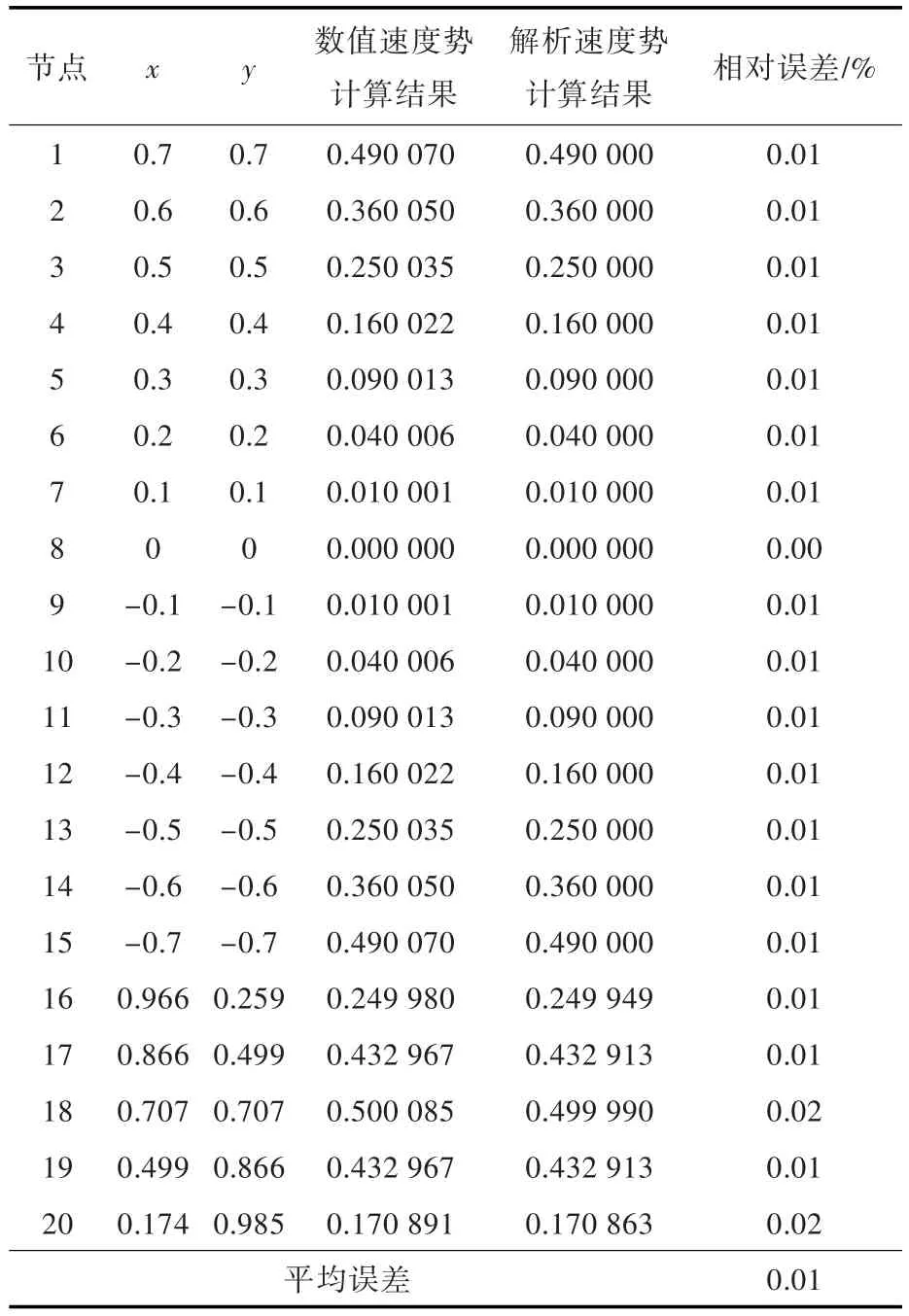
表3 非连续参数化单元速度势计算结果（案例2）Table 3 The calculation results of velocity potential by discontinuous parameterized elements（case 2）

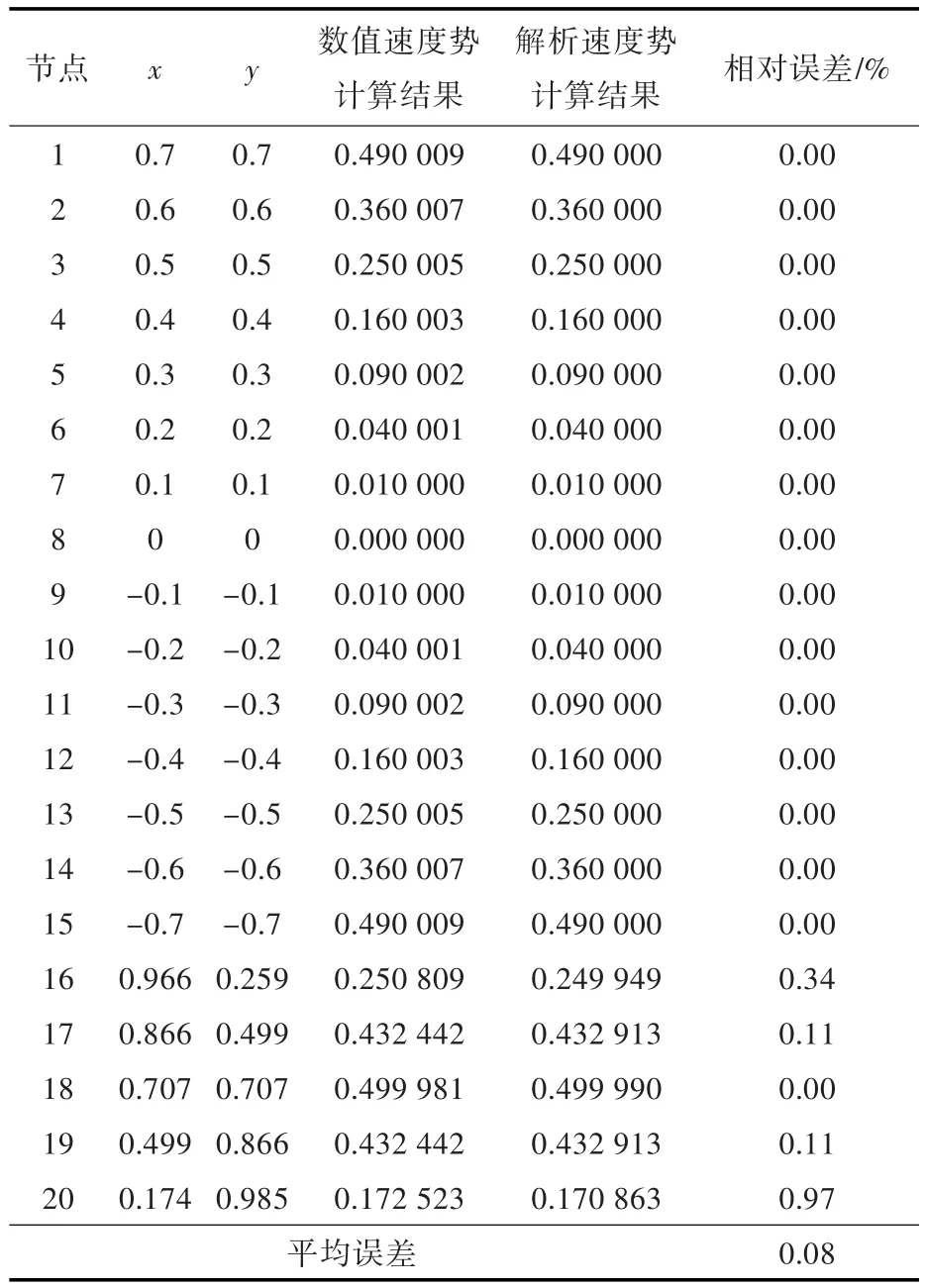
表4 参数化单元速度势计算结果（案例2）Table 4 The calculation results of velocity potential by parameterized elements（case 2）

3 三维势流问题算例

3.1 数学模型

考虑无穷远边界的流场［11-12］，有沿x轴负向的、速度为1的均匀来流。流体无旋、无粘性、不可压缩，流场中有一个半径为1的圆球。流场速度势由下式表示［6］：

式中：Φ0为总速度势；V∞为无穷远处的来流速度；φ为圆球的扰动速度势。将求解的直接变量选择为扰动速度势φ，扰动速度势φ满足定解方程

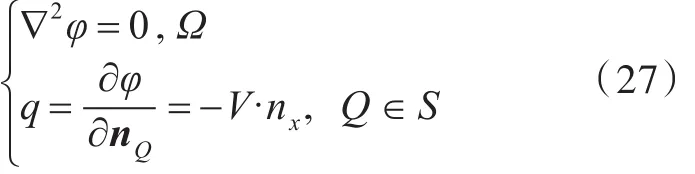
式中：Ω为流场区域；S为物面边界；nQ为Q点的单位法向量。

将基本解ϕ(x，y)=-代入三维边界积分方程，离散并建立方程组，求解方程组后，便可得单元上的未知量。

3.2 离散与数值求解

使用三角形常数单元对求解域表面进行离散，并使用一种对单元上的点进行参数化的方法对问题进行求解。边界积分方程离散后，其求解过程与二维非连续参数化单元类似，此处不再赘述。图4为圆球划分三角网格效果图。

在这里，使用式（28）对单元上的点进行参数化：

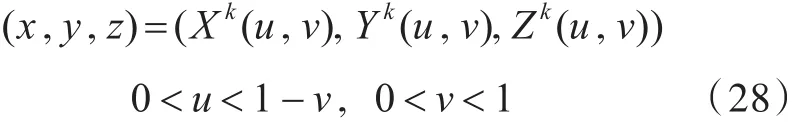
式中：Xk，Yk，Zk为第k个单元上角点坐标的参数化表示；u，v为变换坐标中的量。

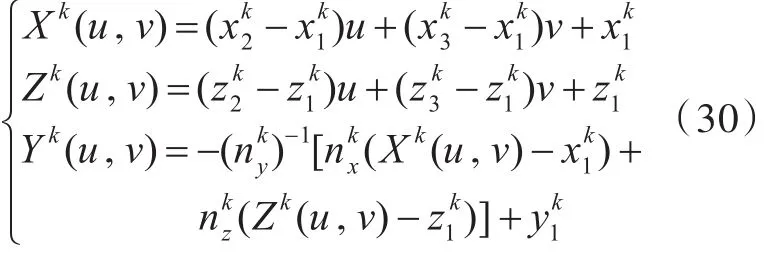
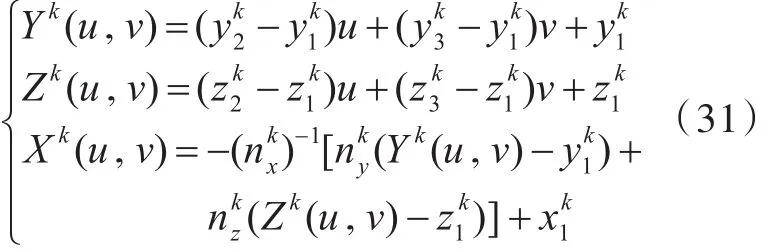
式中，(x1，y1，z1)，(x2，y2，z2)，(x3，y3，z3)分别为三角形元素上角点1，2，3的坐标。

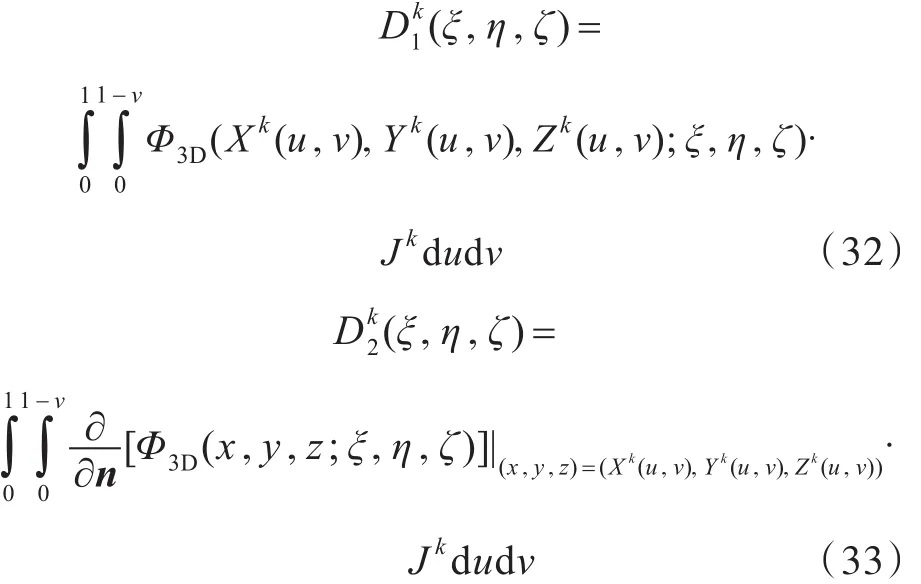
式中：Φ3D为三维拉普拉斯方程的基本解；Jk为雅可比常数，由下式给出：

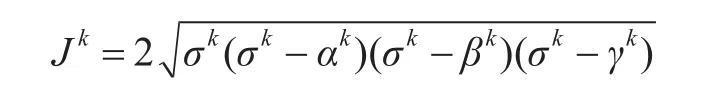
其中，

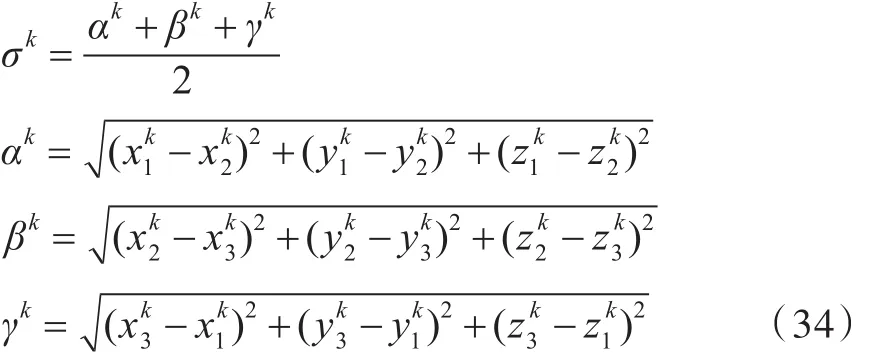
式（32）和式（33）又可以写为式（35）及式（36），其中的t为前面所述的u。

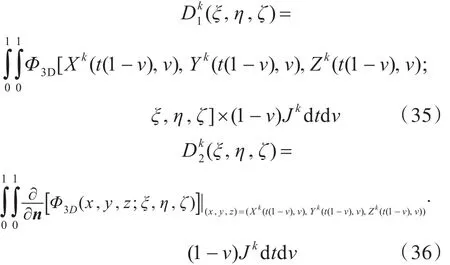
这样，就可以使用高斯积分公式（37）对上式进行数值求解［9］。

图4 圆球划分三角网格效果Fig.4 The effect of sphere divided into triangular grids

3.3 速度求解

求得物面控制点势函数后，使用文献［6］所采用的方法计算物面的速度分布，详细步骤参见文献［13］。

本文选取不同的单元数，分别采用上述方法进行了数值实验，以参数化单元高斯积分法计算系数矩阵的结果如图5～图10所示。图中，相对误差即为相对解析解［11-12］的误差。

当单元数为4 512时，速度势的最大误差为19.76%，平均误差为1.72%；速度的最大误差为29.78%，平均误差为5.18%。

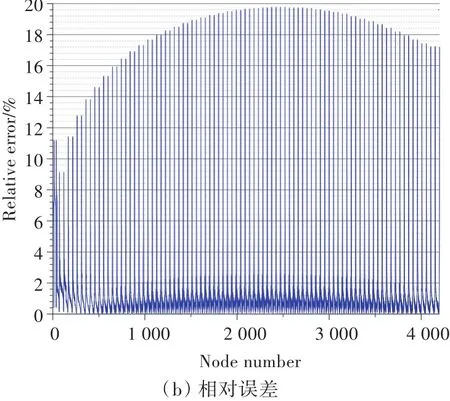
图5 4 512个网格速度势计算结果Fig.5 The calculation results of velocity potential of 4 512 grids

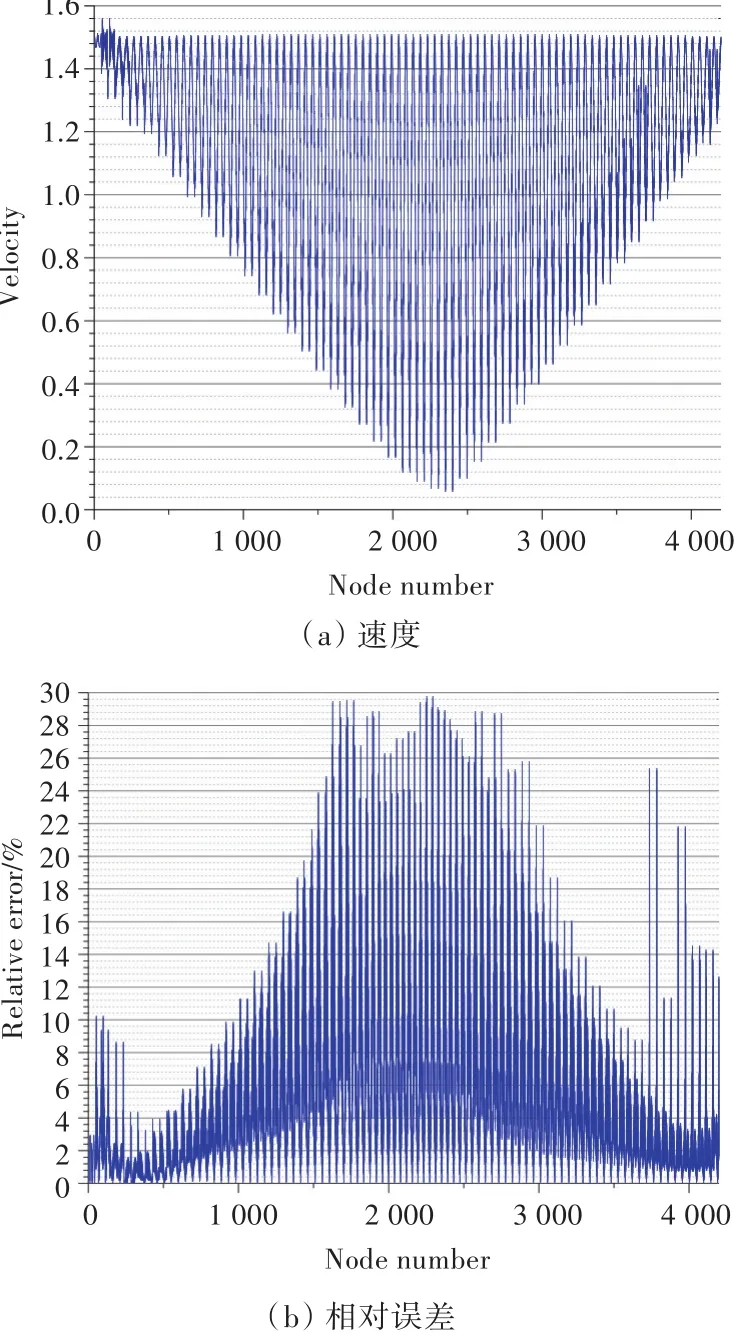
图6 4 512个网格速度计算结果Fig.6 The calculation results of velocity of 4 512 grids

图7 4 512个网格速度矢量结果Fig.7 The velocity vector results of 4 512 grids

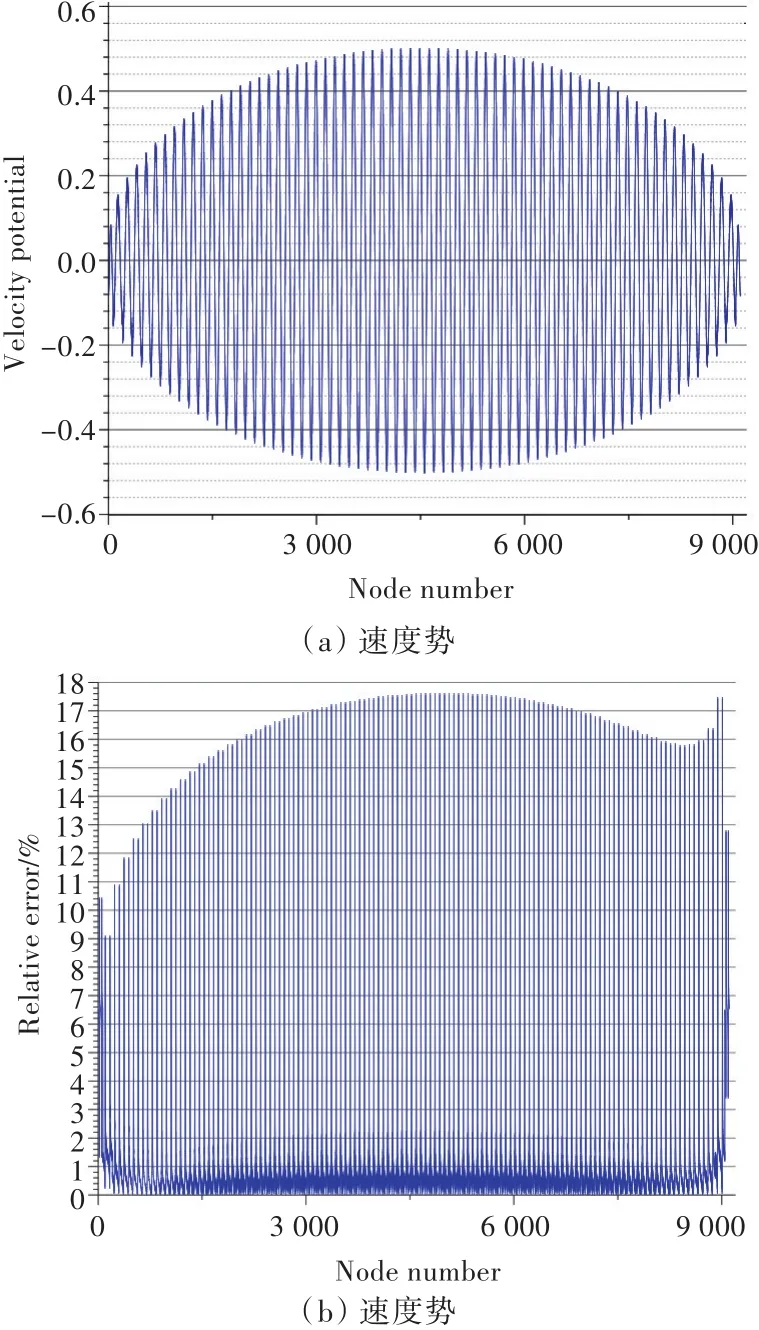
图8 9 112个网格速度势计算结果Fig.8 The calculation results of velocity potential of 9 112 grids

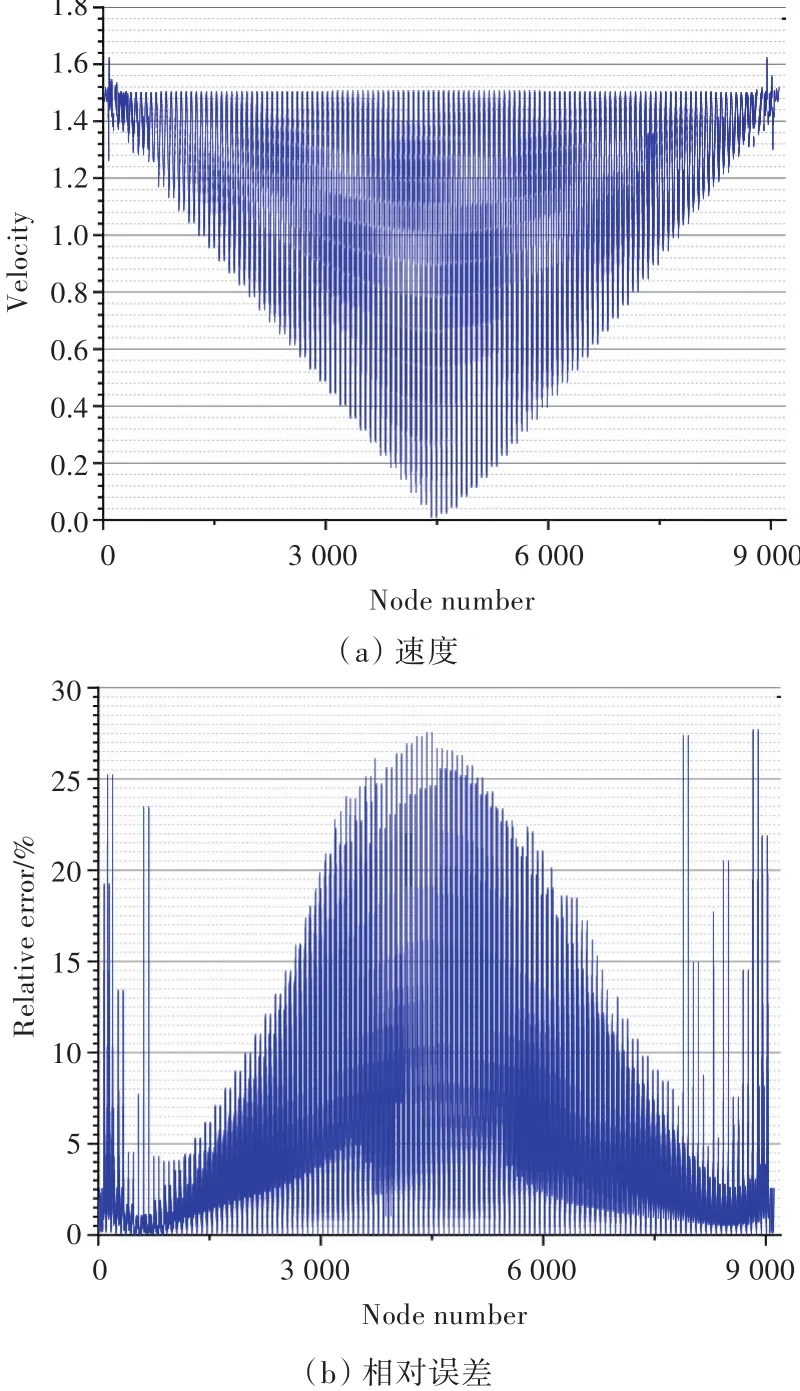
图9 9 112个网格速度计算结果Fig.9 The calculation results of velocity of 9 112 grids

基于网格的划分方法，球的两个极点附近的单元数较少，即便增加总网格数，误差也较其他位置节点处的突出。由于所使用高斯积分公式的数值积分精度不高，因此，三维问题下的计算结果不如二维问题下的好，可以考虑结合采用改进网格划分和采用非连续单元计算，也可以采用其他数值积分方法来提高计算精度。

图10 9 112个网格速度矢量结果Fig.10 The velocity vector results of 9 112 grids

速度幅值计算结果的精度是可以接受的，但该计算结果也未能精确反映解析解给出的速度变化趋势。由图可以看到，速度势和速度的平均相对误差都可以接受，但某些节点的误差偏大。这主要是由引入的高斯积分公式精度不高、数值计算误差所致；另外，不仅速度势函数计算本身存在误差，物面速度计算也存在误差，故可以看到速度势与速度的误差特性有一定的相关性。

当单元数为9 112个时，速度势最大误差为17.62%，平均误差为1.23%；速度最大误差为27.98%，平均误差为4.92%。

数值实验表明，相对于文献［6］的7点高斯积分法，本文方法的优点是计算同数量网格所需时间更少，速度更快；缺点是求解精度存在问题，平均精度尚在可接受范围内，但某些节点的计算误差偏大。通过文中给出的2种情况可以看出，在网格加密的情况下，本文方法的精度提高并不大，数值实验表明，在约4 000网格数时就已达到相当于10 000网格数时的精度，也就是说，求解精度在 4 000网格数左右达到最优结果；在计算机可计算范围内，随着网格的不断增加，计算结果中会出现误差非常大的异常点，笔者认为，这主要是由引入高斯积分公式及参数化单元计算时进行的坐标变换引起单元节点与实际节点不一致所引起。

4 结 语

边界元法的计算量主要集中在影响系数矩阵的计算上，误差也大多源于此。本文对多种参数化单元方法进行了数值实验，分析了各种方法对最终结果误差的影响。

二维下的非连续参数化单元和参数化单元边界元法，由于单元上的节点参数化，矩阵系数计算均为解析式计算，即柯西主值积分，速度快、精度高，没有引起数值计算误差。其中，非连续参数化单元在求解多边界问题时不但兼顾了常数单元交界点无需特殊处理，而且兼顾了二阶及以上单元在较少单元数下得到较高求解精度的优点。

三维下的参数化单元边界元法，由于单元上的节点参数化，计算速度相比于其他方法稍快，但矩阵系数计算引入了高斯积分公式，引进了数值计算误差，在计算系数积分时进行了坐标变换，使得变换后求得的单元节点与实际节点存在偏差，故又引入了新的误差。数值实验表明，计算平均误差可以接受，但存在着某些节点的误差偏大的问题，易导致求解不够精确。可以通过改进网格划分和采用非连续单元计算，或其他可通过坐标转换进行解析计算的单元来计算。

本文的二维非连续参数化单元可以用于对波浪与浮体，或者潜体的作用机理进行研究，单元数少，求解精度高；三维参数化单元虽然求解精度差，但求解速度快，若进一步改进，如非连续单元在三维时，可提高运算精度。

本文所涉及的参数化单元边界元法的编程与传统边界元法的编程程序相比具有通用性，可以解决一类在势流框架下的工程及科学问题。