尼尔基水库非枯季节中期入库径流预报研究

白云天 ，孟祥国 ，孙万光

（1.嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔161005；2.嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔161005；3.中水东北勘测设计研究有限责任公司科学研究院，吉林长春130061；4.水利部寒区工程技术研究中心，吉林长春130061）

尼尔基水利枢纽位于黑龙江省与内蒙古自治区交界的嫩江干流中上游，水库坝址距离嫩江河口585 km，控制流域面积66 382 km2，占嫩江流域面积的22.35%。坝址处多年平均年径流量为104.7×108m3，约占嫩江流域年径流量的45.7%。尼尔基水利枢纽是嫩江流域集防洪、供水、发电、航运、水环境保护于一体，综合利用效益十分显著的大型控制性工程，水库调节库容59.68×108m3，径流调节能力突出，为多年调节水库。较准确的入库径流预报可为水库调度提供决策依据，对充分发挥枢纽的防洪及兴利效益具有十分重要的意义。

嫩江及尼尔基水库坝址以上流域长期径流预报已取得了比较丰富的研究成果。李鸿雁对嫩江流域径流的大气环流影响及其敏感性和相关性进行分析，并对嫩江流域径流的可预报性及其时间尺度进行了深入的研究[1-3]，认为采用大气环流因子进行入库径流预报适用的时间尺度一般为月。周长美采用前后期径流相关法对尼尔基水库枯季入库径流进行预报[4]，并取得了比较满意的结果。尼尔基水库枯季（11月至翌年3月）入库径流预报因流域降水主要以固态形式存在于流域内，不参与水循环，径流主要以河网和地下水退水为主。但非枯季节（4—10月），入库径流受降水、融雪、退水等因素影响，使入库径流预报变得十分复杂。尼尔基水库非枯季节中期入库径流预报对枢纽的兴利调度特别是发电调度意义重大，但目前可用于作业预报的入库径流预报方法一直比较匮乏。本文拟对入库径流影响因子进行筛选，采用数理统计方法对尼尔基水库非枯季节中期入库径流进行预报。

1 预报模型简介

入库径流预报通常建立自变量与多因变量之间的相关关系数学模型，归纳起来可分为两类：线性模型和非线性模型。线性模型中，多元门限回归模型较其他模型具有一定优势[5]：它通过设置门限元数量，能有效描述具有突变性、准周期性、分段相依性等复杂问题，以分区间的线性模型来表述研究对象在整个区间的非线性变化特征，也可以解决具有一定非线性的问题。非线性模型中[5]，投影寻踪模型以其模型结构简单、稳健性好而得到广泛应用。

1.1 多元门限回归模型

多元门限回归能有效地描述具有突变、准周期性、分段相依等复杂现象的非线性动态系统。其基本思想是：当给出预报因子资料后，首先根据门限变量和门限值决定在不同情况下使用不同预报关系的方程，以此解释各种类似于突变的现象。其实质是，把预报问题按状态空间的取值进行分类，用分段的线性回归模型来描述总体非线性问题。

设预报对象 yt与因子 x（ti）构成的非线性模型形式为：

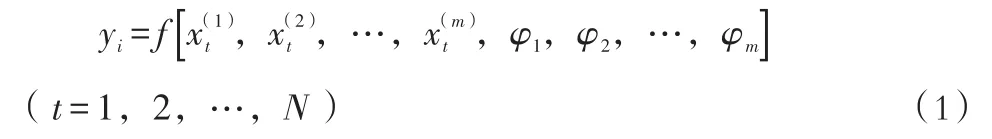
式中：N为样本容量；m为因子数；φ1，φ2，…，φm为待定参数。

若其中有某个特殊因子x（i），当其值低于某个水平时，预报对象与预报因子之间是一种函数关系，而当其值高于某个水平时，预报对象与因子之间又是一种函数关系，则称x（i）为门限变量，导致预报对象与因子函数关系改变的

xk（i））（1＜k＜N）值称为门限值。

根据门限变量将预报对象和预报因子分为L段，将每段进行多元回归分析，其数学模型如下：

式中：rj(j =1，2，…，L-1)为门限值；L为门限区间个数；φ(j ， s)(s =1，2，…，m )为第 j个门限区间内的回归系数；y(i)为预报对象序列；x(s ， i)(s =1，2，…，m )为预报因子序列，m为预报因子个数；x(k ，i)(1 ≤k≤m )为门限变量；d为门限延迟步数；ε(j ， i)为白噪声。

1.2 投影寻踪模型

投影寻踪是用来分析和处理高维观测数据，尤其是非线性、非正态高维数据的一种新兴人工智能技术，它通过把高维数据投影到低维子空间，寻找能反映原高维数据结构或特征的投影，达到研究分析高维数据的目的。其中心思想是：找到若干个投影方向，将高维数据投影到一维空间后，用若干个岭函数加权和的形式来逼近回归函数。投影寻踪回归方法的数学表达式为：

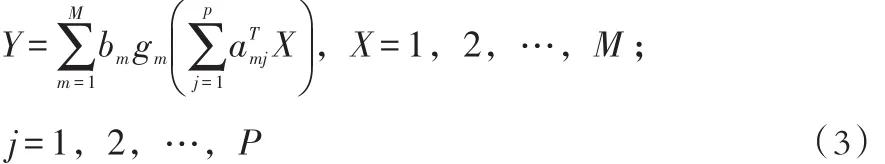
式中：Y为因变量；m为逼近的子函数个数；gm为第m个光滑岭函数；bm为权值，表示第m个岭函数对输出值的贡献大小；amj为第m个投影方向的第 j个分量；p为输入空间的维数；要求

投影寻踪回归的实现，是对参数步步寻优，对回归函数的结构形式无太大依赖关系，回归模型对系统信息的识别由3个参数来实现：投影方向a、岭函数g、权重b。实现投影寻踪回归的核心问题有两个：

1）投影问题。实现投影寻踪回归的第一步就是通过对系统信息的分析，得到最能反映系统特征的投影方向，投影的过程必须实现两个目标分别为降低维数和投影方向能够反映系统特征。

2）寻踪问题。样本序列投影到低维子空间后，为避免信息的重复利用引起的过度拟合问题，需要在已有的岭函数中，优选其中最能表达系统特征的岭函数，写进最后的加权和式（3）中，这个过程称为寻踪，其目标是确定模型的最优岭函数的值。

投影寻踪回归方法包括参数方法和非参数方法。由于非参数回归模型要求大量样本才能实现无偏估计，对于资料短缺的水文水资源预测而言，用基于非线性的Hermite多项式的参数投影寻踪回归模型较为合适，其优越性已被大量的实践所证实。

2 预报因子筛选

旬径流预报是在预报因子中加入未来一旬气象预报信息。由于没有流域气象预报的历史数据，降雨预报数据采用历史实测降雨代替，气温采用嫩江气象站实测数据。在预报因子筛选过程中发现，一般情况下，引入气象预报信息均能不同程度地提高预报精度，但由于气象预报信息具有不确定性，若引入气象预报信息相关的因子不能显著提高预报精度，则将该因子剔除。经筛选后确定各旬预报的预报因子，如表1所示。

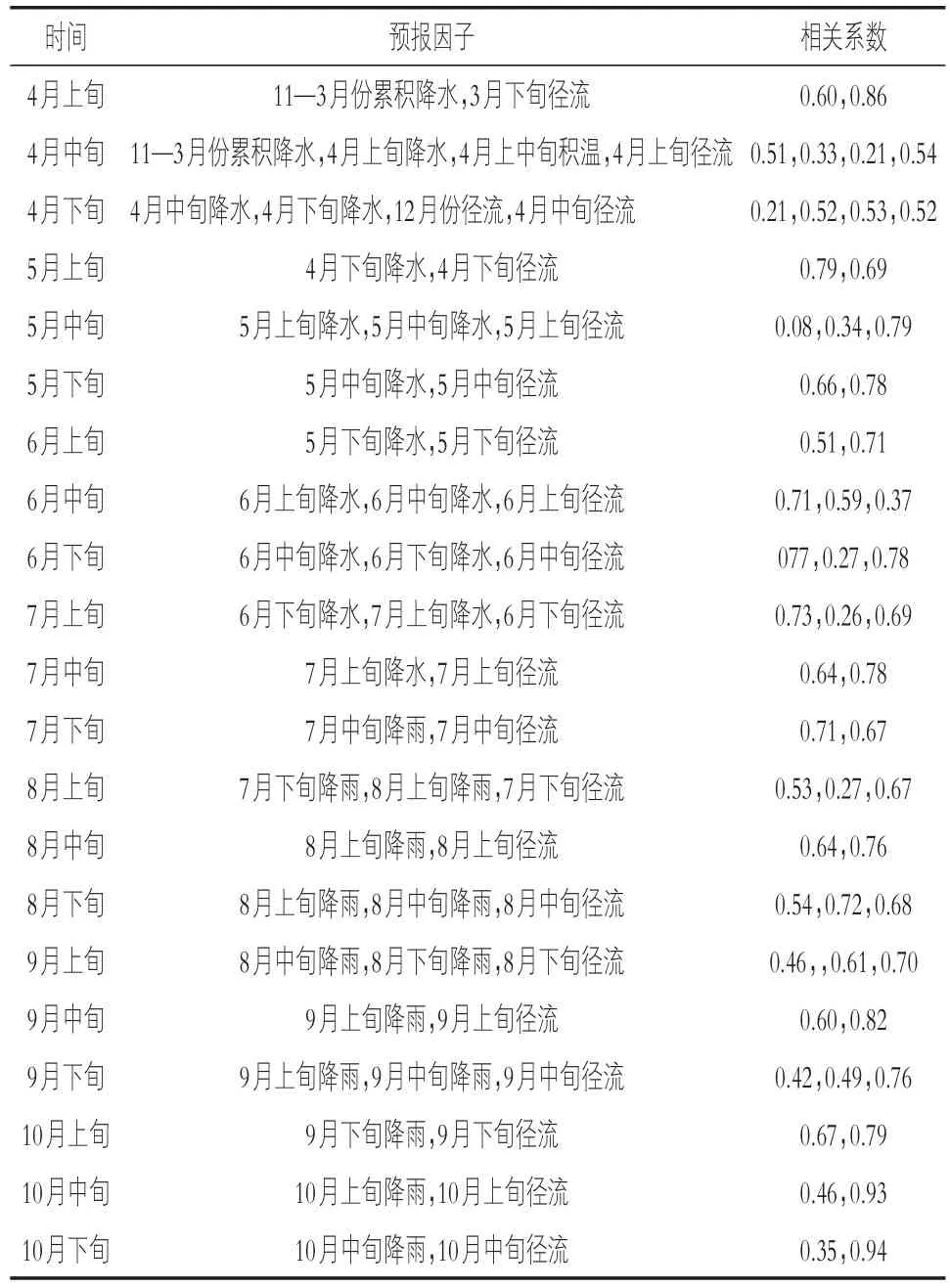
表1 旬径流预报预报因子表

由表1可知，除4月中旬和6月中旬外，旬径流一般与前一旬的降水和径流关系最为密切，与本旬的降水相关关系并不强。这是因为尼尔基水库以上流域面积较大，汇流时间长所致，故所建立的旬径流预报模型预报精度受气象预报精度的影响不大。

3 预报成果分析

根据水文气象资料情况，采用选定的预报因子，利用1970—2003年的资料训练模型参数，利用2004—2013年10年的资料进行预报检验。为使建立的模型具有代表性，在选择训练样本时剔除了存在极端特大值的样本，如6月下旬径流预报中剔除了1998年的样本。分别采用多元门限回归模型和投影寻踪模型进行了模拟预报，当两种预报模型模拟结果无显著性差别时，推荐采用稳定性较好的多元门限回归模型。推荐模型的模拟预报结果如表2所示。

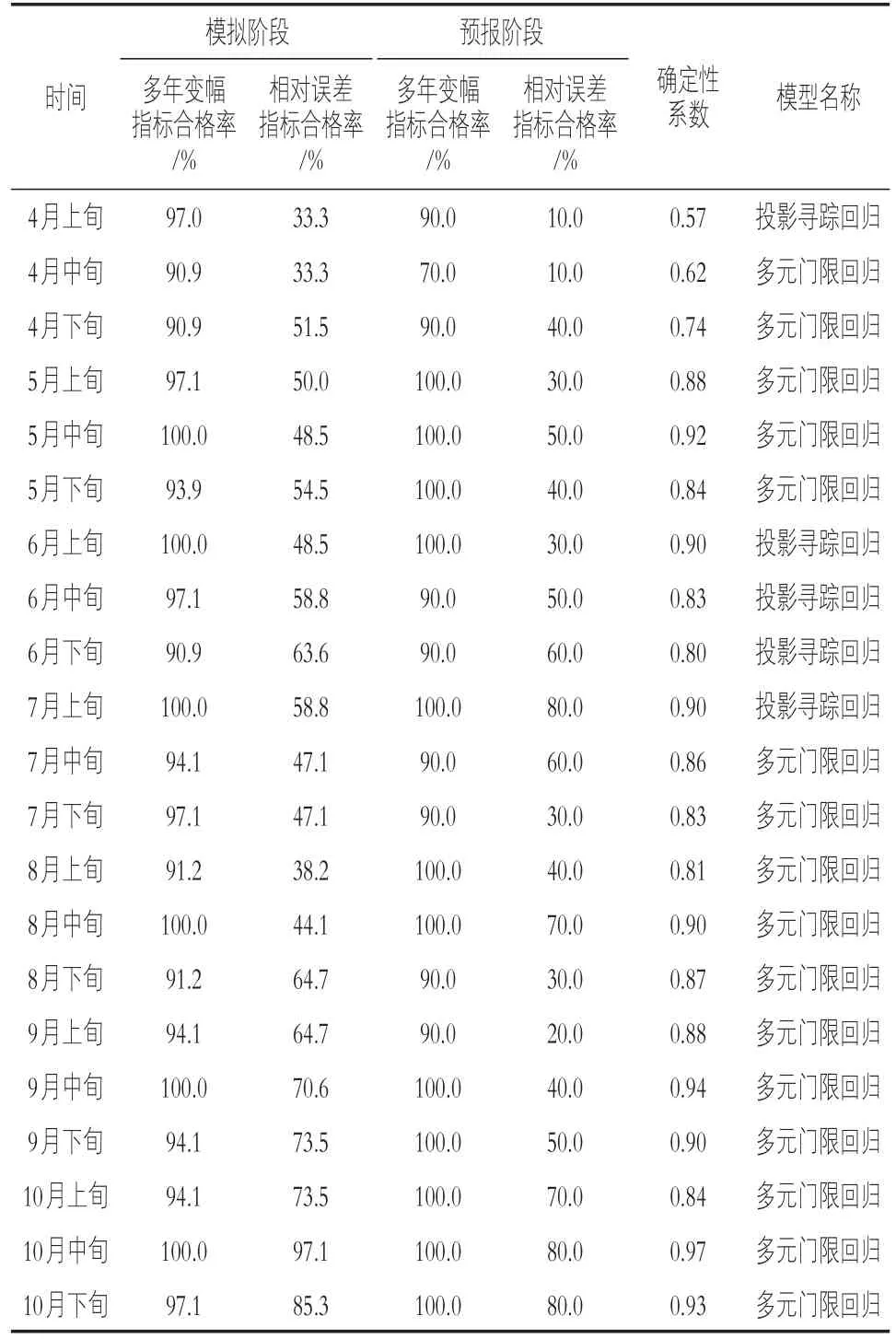
表2 旬径流预报精度评价表

按照《水文情报预报规范》的相关规定，本次旬径流预报精度除4月中旬预报合格率低于80%外，其他各旬预报精度均大于80%。若将历史旬同期的径流时间序列视为一个径流过程，从确定性系数判断，除4月上、中旬确定性系数低于0.7外，其他各旬均为大于0.7或0.8。这表明所建立的旬径流模型能够反映尼尔基水库流域径流变化规律，可用于作业预报中。

4 结论

1）利用数理统计方法进行旬径流预报时，预报因子宜按表1选用。除4月中旬和6月中旬外，旬径流一般与前一旬的降水和径流关系最为密切，与本旬的降水相关关系并不强，且在预报因子筛选过程中，未选入不能显著提高模型预报精度的与气象预报信息相关的因子，故所建立的旬径流预报模型预报精度受气象预报精度的影响不大。

2）采用数理统计方法进行旬径流预报时，根据预报时段，推荐按表2选择相应的预报模型。按照《水文情报预报规范》的相关规定，旬径流预报精度除4月中旬预报合格率低于70%外，其他各旬预报精度均较高。若将历史旬同期的径流时间序列视为一个径流过程，从确定性系数判断，除4月上、中旬为低于0.7外，其他各旬均达0.7甚至0.8以上，模型模拟预测值与实测值的变化过程有良好的一致性，表明所建立的旬径流模型能够反映尼尔基水库流域径流变化规律，可用于作业预报。