基于回归分析的长春市需水量预测研究

金冬梅，荣 楠

（1.吉林省水资源服务中心，吉林长春130000；2.吉林省老龙口水库管理局，吉林珲春133300）

到20世纪末，在我国600多座城市中[1]，已经有近2/3城市不同程度存在供水不足的问题，其中，有110个城市达到比较严重的缺水程度，全国缺水总量为60×108m3[2]。每年由于缺水造成的直接经济损失达3 500×108元，其中，全国城市工业每年损失近2 000×108元[3]。随着社会的不断发展，水资源变得越来越重要，逐步成为一个城市、一个国家乃至全球发展的制约因素。长春市所在流域内人口众多，工农业生产发达，用水量大，水资源开发利用程度较高。根据多年供用水资料统计，长春市多年平均总用水量占当地水资源量的71.0%，水资源短缺已成为长春市社会经济持续发展的瓶颈。对长春市的用水系统进行中长期的预测，可以为长春市的产业发展及城市规划提供有力依据，既可以促进长春市建设节水型社会，又可以为其他城市的发展提供有利的参考依据。

城市需水量预测方法有很多，根据对数据的处理方式的不同，城市需水量的预测方法大体上分为系统分析方法、结构分析法、时间序列法及组合法4种，其中回归分析法具有操作简单，实现容易，可控性强的优势。利用多元线性回归分析模型预测城市需水量，可以确定各个影响因子对城市需水量的影响，进而可以通过调整影响因子降低需水量，为城市节水实现节水型社会提供可靠性建议。

1 多元线性回归分析[4]

回归分析法是结构分析法的重要组成部分，分为一元线性回归分析、多元线性回归分析和非线性回归分析3种方法，其中，使用最多的是多元线性回归分析法。

多元回归分析法是以数理统计分析为基础的分析方法[5]，则其线性回归模型为：

式中：β0，β1，…βm，σ2—— 为与 x1，x2，…，xm无关的未知参数；β0，β1，…βm——为回归系数。

现有n个独立观测数据 (yi1，xi1，…xim)，n＞m

由式（1）可得：

式中：i=1，2，…，n。

记

令ε=[ε1… βn]T，β=[β0β1… βn]T

公式（1）可以表示为：

式中：En——为n阶单位矩阵。

得残差平方和Q：

经过整理，得到下面的正规方程组：

正规方程组的矩阵形式为：

当矩阵X列为满秩时，XTY满足可逆矩阵条件，式（7）的解为：

β∧服从正态分布

对残差平方和Q，EQ=(n -m-1) σ2，且

式中：S2——是剩余平方差（残差的方差）；S——称为剩余标准差。

对原始数据yi的总变异平方和SST=

式中：U——为回归平方和；—y —为实际值的均值。

回归模型主要进行2种检验，分别为：方程显著性检验（F检验）和拟合优度检验（R2检验）[6]。

确定因变量和自变量之间的线性关系是否具有显著，即检验是否大多数因变量都可以被自变量解释的检验称为方程显著性检验[7]。

Q，U满足如下关系：

在显著水平α下，有上α分位数Fα(m ，n-m-1)，若F＜Fα(m ，n-m-1)，接受H0，即线性关系不显著，因变量不能被自变量解释，方程不成立，模型不适用；否则，拒绝，即线性关系显著，因变量可以被自变量解释，方程成立，模型使用。

确定拟合的多元线性回归方程与数据的拟合程度的检验为方程拟合优度检验，拟合优度高方程适用，拟合优度低方程不适合使用。

R2定义为：

R越大，表示X1，…，Xm与Y的相关关系越密切，即模型越适合使用通常，R大于0.8才认为相关关系成立。

2 回归分析预测需水量

2.1 建立模型

长春市的需水量受很多因素的影响和限制，由于资料限制，收集2000—2016年17年的用水量、GDP及人口资料，以2000—2012年13年的人口、GDP为自变量，用水量为因变量，利用多元线性回归模型进行分析，建立需水量回归模型，以2013—2016年数据进行检验，得到多年用水量的多元线性回归模型如下：

式中：Y——年需水量，108m3；X1——人口，106人；X2—— GDP，1010元。

根据式（20）对长春市2000-2012年用水量进行计算，计算结果见表1及图1，2。

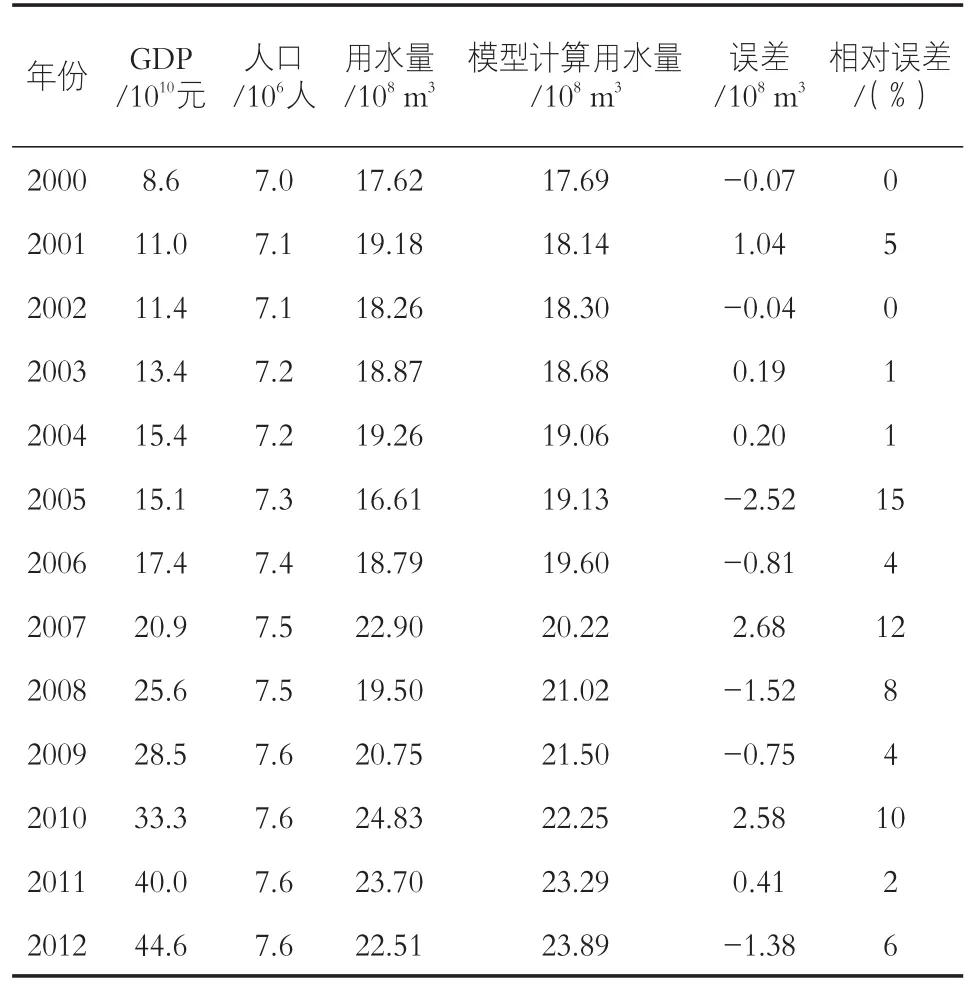
表1 长春市2001—2012年需水量多元线性回归计算结果表

图1 多元线性回归年需水量数据拟合图

图2 多元线性回归模型预测残差图

从图2可以看出，残差值均围绕零点附近上下分布，说明回归直线对需水量数据拟合情况良好。

2.2 多元线性回归模型检验

多元线性回归模型的检验主要包括拟合优度检验（R2检验）、方程显著性检验（F检验）2种检验方式。

2.2.1 拟合优度检验

经计算，观测数据的均值—y =20.2，根据公式（14）计算U=48.99，根据公式（10）计算 Q=26.99，根据公式（10）计算 SST=76.09，根据公式（18）计算R2=0.64，根据公式（19）计算R=0.8，模型适合使用。

2.2.2 方程显著性检验

在显著性水平α为0.05，样本数据n1=1，n2=11的情况下，有：

根据公式（17）计算F=26.17，F＞F0.（051，11）说明方程回归效果显著，即用水量与GDP、人口之间的线性关系显著，模型适合使用。

以2013—2016年数据进行检验，检验结果见表2。

表2 模型检验结果

2.3 应用模型预测城市需水量

根据《长春市总体规划2011—2020》，规划长春市2020年地区生产总值为10 000亿元。根据长春市2001—2012年的人口数量及历年人口增长率，除考虑城市人口的自然增长外，还考虑了城市发展人口的机械增长，取平均人口增长率6.59‰为增长率，则长春市2020年人口预测值为797.74万人。

根据公式（20），预测长春市2020年城市年需水量32.72×108m3。

3 结论

应用多元线性回归模型预测预测2013—2016年需水量，经过检验模型适用，模型对长春市2020年城市年需水量进行预测，预测结果为32.72×108m3。

根据吉政明电〔2016〕72号文长春市2020年用水总量指标为28.5×108m3，可知现状用水条件下需水量超过2020年要求，需采取一定的节水措施。