信用支付策略下库存影响需求的供应链协调
李瑶,闵杰,欧剑
(1.安徽建筑大学 经管学院,安徽 合肥 230601;2.安徽建筑大学 数理学院,安徽 合肥 230601)
0 引 言
在类似超市的一些零售系统中,商品的需求可能受其库存水平影响,这种现象称为库存水平影响需求率(inventory-level-dependent demand)[1,2].文献[3]第一个建立了需求是库存水平线性函数、缺货完全补充和有限生产能力的变质性物品库存模型,文献[4]对文献[3]进行扩展研究,按不允许缺货、允许缺货且完全补充和部分补充建立三个相应的库存模型,给出了模型数值解;文献[5,6]将通货膨胀考虑到模型中,文献[7,8]则建立了信用支付的库存模型.文献[3-8]都是对单个企业的库存模型进行研究,但是随着全球经济朝着一体化发展,现代企业竞争不再是单一企业的竞争,而是企业所处的供应链之间的竞争,因此供应链协调研究已受到许多研究人员的重视.文献[9]最早建立了由一个供应商和一个零售商或两个相互竞争的零售商组成的供应链协调模型,给出了货架线性补贴的协调策略.文献[10]考虑需求的依赖库存行为而创建了相应的离散事件系统仿真模型,设计了一种基于仿真的种群重叠、遗传操作非重叠的进化算法,用于优化库存控制策略.文献[11]研究了需求是库存水平幂函数的供应链协调模型,而文献[12]建立了市场需求是库存水平线性分段函数、变质性产品的供应链量折扣协调模型.
信用支付在商业活动中广泛使用,它是指制造商(卖方)给零售商(买方)在货款支付期限方面的优惠,在信用支付期限内买方不需要支付利息.信用支付作为一种短期商业信贷主要方式,广泛地存在于商业活动中.目前,大多数关于信用支付研究都是基于库存模型框架下进行分析的.文献[13]首先提出了允许信用支付的经济订货批量(economic order quantity,EOQ)模型,文献[14]考虑了供应商同时给予信用支付和现金折扣情况下零售商最优决策.文献[15,16]则在经济生产批量(economic production quantity,EPQ)框架下分析了信用支付模型,提出了零售商最优采购周期确定的算法.文献[17,18]分别进一步考虑了信用支付期限与订货量相关的情况.文献[19]研究了信用支付条件下变质产品有限补货周期和需求价格敏感的合作库存模型,并指出信用支付策略是合作系统中利润共享的双赢策略,文献[20]在给定延期付款期限和需求依赖于库存情况下,给出零售商最优付款时间的模型.文献[21]考虑了供应商给予零售商信用支付,同时零售商给予顾客信用支付的决策模型.有关利用信用支付文献[22]研究了利用信用支付和利润共享的供应链协调问题,文献[23]则建立了由单制造商和多零售商组成的信用支付的供应链协调模型.
但是以上研究成果并没有将信用支付和货币时间价值应用到库存水平影响需求的供应链协调问题上,因此本文考虑由单一制造商和单一零售商组成的两层供应链,制造商生产并批发某一产品给零售商,零售商面临的市场需求线性依赖于该产品的库存水平,研究作为Stackelberg博弈的主导者,制造商如何利用信用支付策略来激励零售商合作从而实现供应链协调运作问题,建立了一个可以协调供应链的信用支付模型,给出了相应的算法,数值算例结果也表明该模型和算法对实现供应链的协调运作是有效的.
1 模型假设与记号
本模型作如下假设与记号:
(1)考虑由单一制造商和单一零售商组成的两层供应链,其中制造商生产并批发某一产品给零售商,假设制造商与零售商之间进行以制造商为主导的Stackelberg博弈;
(2)需求信息与成本信息均对称;
(3)假设零售商按EOQ模型来确定其最优订货量,零售商将订购的商品全部销售完后立即进行下一次补货,且补货率无穷大(亦即制造商生产率无穷大);
(4)假设制造商与零售商之间实行“批对批”策略,因此在制造商处不考虑库存费用;
(5)假设市场需求率D(t)线性依赖于零售商的当前库存水平,即
D(t)=α+βI(t),
其中α>0表示基本需求率,β>0表示需求受库存水平影响的因子,I(t)为零售商在t时刻的库存水平;
(6)c表示制造商生产单位产品的成本;w表示制造商给予零售商的单位商品的批发价格,而w*是制造商未实施信用支付策略前的最优批发价格;p表示单位商品的零售价格,且假设p>w>c;
(7)Ar表示零售商每次订货的固定订货费用,Am表示制造商每次生产的准备费用,h表示零售商单位时间单位货品的库存费用,不包括库存资金的成本;
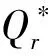

(10)制造商提供零售商延期付款策略计划,M表示允许的信用支付期(决策变量);
(11)Ip为零售商单位库存单位时间的支付利息,Ie为零售商单位库存单位时间的收益利息(Ie 由假设(5)可得零售商处的库存水平变化的微分方程可表示为: (1) 注意到边界条件I(0)=Q,则式(1)的解为 (2) 由式(2)可得零售商每个订货周期的长度为: (3) 为了得到一个基准,我们首先考虑供应商和零售商属于同一企业,即一体化情形.一体化供应链系统的平均利润为: (4) 将式(2)和式(3)代入式(4)可得 (5) (6) (7) 当β(p-c)-(h+Ip)≥0时,Πc(Q)是关于Q的递增函数,此时供应链系统最优订货量为无穷大,这与实际情况相矛盾,所以本文假设β(p-c)-(h+Ip)<0. (8) (9) (10) (11) 由极值存在的必要条件知,最优批发价格w*必满足方程“dΠm(w)/dw=0”.式(11)对w求导得 (12) 其中 通过上面的分析,可得如下定理1. 和 因为f(X)=XlnX-X+1严格递增函数,且 由定理1可知,制造商和零售商独立决策时的订货量小于联合决策时的订货量,因此整个供应链的利润没有达到最大化,即供应链处于一种失调状态,因此作为供应链的主导者,制造商有激励零售商多订货以实现自身利润最大化和供应链协调的动机.下面我们考虑供应商如何用信用支付手段来协调供应链系统. 假定制造商给予零售商一个信用支付期限M,使得零售商在该策略下能够增大订购量,此时零售商的利润函数由以下部分组成: 1)每个周期的固定订货费用为Ar; 5)每个周期在信用支付期限到期后零售商为仍未出售的货物款而支付的利息可分为以下两种情形: (i)若0≤T≤M,由于订货周期不大于允许的信用支付期,显然此时要付的利息为0; (ii)若T>M,因为订货周期大于信用支付期,所以零售商在时间段[M,T]内要为仍未售出的货物款而支付利息,其值为: 6)类似于5),每个周期零售商在信用支付期内赚取的利息也分为以下两种情形: (i)若0≤T≤M,则零售商在时间段[0,T]内可以边销售边赚得利息,而在时间区间[T,M]内,零售商可以利用所有的销售收入来赚得利息,因此在信用支付期[0,M]内零售商所赚的利息为: (ii)若T>M,则零售商只能在时间段[0,M]内可以边销售边赚取利息,因此在信用支付期M内零售商所赚取的利息为: 由1)-6)可得零售商单位时间内的平均利润为: 其中: (13) (14) 式(13)和式(14)是关于T的单变量函数,其中又含有制造商的决策变量M.对ΠrM(T)关于T求一阶导数可得: (15) (16) 由极值存在的必要条件知,在信用支付策略下零售商的最优订货量一定是式(15)或式(16)的零点.此时,若零售商的利润大于分散决策时自己的利润,那么他就会接受此协调策略.另一方面,在实施信用支付策略时制造商必须保证自己的利润不受损失,为此要分析信用支付策略下制造商的利润. 对于制造商而言,当给予零售商信用支付优惠后其利润由以下部分组成: 1)每次生产或订购的固定费用为Am; 所以,当实施信用支付策略后制造商的平均利润函数可表示为: (17) 由式(3)知Q是关于T的增函数,如果零售商在接受延期付款策略后的订货周期大于独立决策时的订货周期,那么制造商在实施信用支付策略后零售商的订货量大于独立决策的订货量.下面我们从订货周期T出发来证明信用支付策略会使零售商加大订货量. 将式(3)代入到式(6),可得零售商在独立决策时关于T的方程: (18) 令式(15)和式(16)为0,可得实施信用支付策略后零售商订货周期T所满足的方程: (19) (20) 由f(T)是T的增函数,所以如果 (21) 且 (22) 现在考虑如何保证制造商的利润不受损失.当实施信用支付策略后制造商的平均利润必须大于独立决策下制造商的平均利润,即ΠmM(T)>Πm(T),则等价于 (23) 由于式(21)和式(22)的复杂性,本文将通过数值算例来说明制造商通过信用支付策略来协调供应链的有效性和可行性.首先我们给出上述模型求解的步骤和算法. 第二步:根据dΠm(w)/dw=0求出最优订货价格w*; 第四步:由式(21)、式(22)和式(23)求出信用支付期M的取值范围; 第五步:求出实施延期付款策略后制造商的平均利润ΠmM(T),若在信用支付期M下双方的利润都没有受损,此时供应链的利润得到增加,则此策略是有效的; 第六步:若在信用支付期M下至少有一方的利润受损,则此策略是无效的,此时需重新调整延期付款期M. 信用支付在商业活动中广泛使用,它是促进和改善供应链协调运作的有效手段之一.本文针对市场需求受库存影响的情况下,建立了制造商如何利用信用支付手段来协调供应链模型与算法,理论分析和算例结果都表明利用信用支付策略来实现供应链协调是有效的和可行的,同时也为供应链管理决策提供了各种选择.但是本文只考虑由单一制造商和单一零售商组成的两层供应链和信息对称等情形,对于多制造商、多零售商、非对称信息、允许缺货以及其他需求形式等情况是下一步研究的主要方向.2 模型的建立与求解

2.1 一体化供应链系统
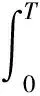
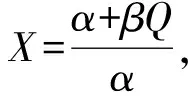
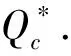
2.2 各自独立运作的供应链系统
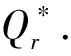
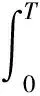
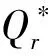
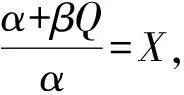

2.3 协调供应链的优化模型
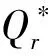
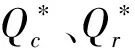
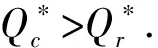
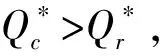
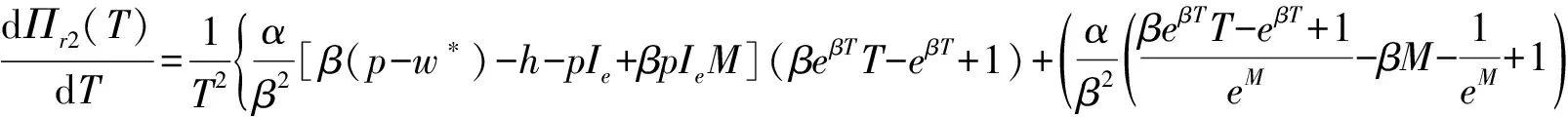
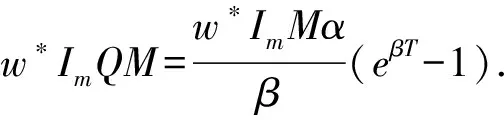

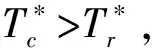
3 算法与数值例子
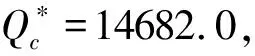
4 结束语

