有源配电网的全象限安全域研究
孟繁淞 严雪松 张 捷
(国网天津市电力公司客户服务中心,天津300000)
0 引言
随着社会和经济发展不断深入,环境污染和能源使用安全性问题亟待解决,配电系统中可再生能源的并网成为重要发展趋势。因此,有必要找到电力系统安全运行的边界,从而保障可再生能源的高比例并网[1]。
本文提出了全象限配电安全域(TQ-DSSR),将安全域从第Ⅰ象限延伸至四个象限,相应的数学模型及算法产生巨大的变化,需在现有模式下,扩充更新安全域整个理论架构体系[2-3]。
因此,本文研究有源配电网的安全性,建立全象限安全域模型,用算例分析归纳TQ-DSSR的性质特点。
1 有源配电网的N-1安全约束
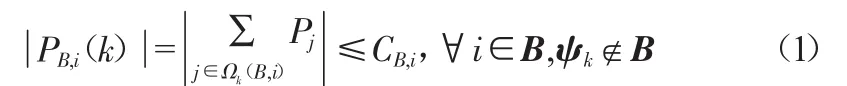
在全新运行的拓扑结构中,PB,i(k)为线路Bi的功率,Ωk(B,i)为线路Bi的汇总节点处。该公式是指,当元器件ψk因意外不运行后,任何一条线路的容量都要大于等于下游所有节点的功率值。
(2)N-1主变的容量约束:

元器件N-1以后,有源配电网需重新建立全新运行的拓扑结构,该元器件的功率平衡方程将随之改变。
(1)N-1线路的约束方程:
在全新运行的拓扑结构中,PT,i(k)代表主变压器Ti的功率,Ωk(T,i)则代表主变压器Ti的汇总节点。该公式是指,当ψk不参与运行后,任何一个主变压器i容量都要大于等于下游所有节点的功率值。
假设Ψ是所有故障的集合,W是某工作点,∀ψk∈Ψ,式(1)和(2)均成立,则W符合N-1安全准则[4-6]。
2 有源配网的全象限安全域模型
TQ-DSSR是指一个集合,在该集合的状态空间里,包含正常运行条件下的工作点以及N-1安全准则的工作点。根据公式(1)和(2),TQ-DSSR模型可用公式(3)表示:

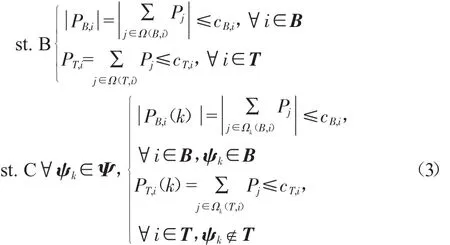
根据上式可知,和传统的DSSR相比,TQ-DSSR数学模型的特征具体表现在以下两点:一是该公式含有绝对值,有源配电网的安全运行边界可以在四个象限;二是状态空间状态量需涵盖所有四个象限[7-8]。
3 算例验证与分析
3.1 算例验证结果
通过平面二维可视化研究TQ-DSSR。按照上述TQ-DSSR模型给定边界运行方程,确定两个变量,保持其余量不变,将方程显示在坐标系里。可以发现,该模型有四种图案,三角形、长方形、梯形以及五边形。
五边形如图1所示。
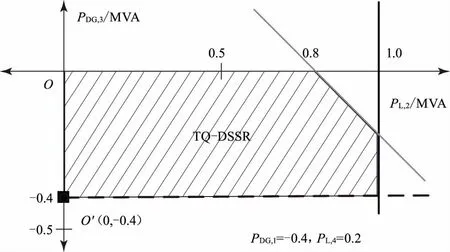
图1 有源配网(TQ-DSSR)截面:五边形
通过修改PDG,1、PL,4数值,平行移动灰色线条依次可得梯形、矩形和三角形。
3.2 安全性质
根据四种图案,深入研究全象限安全域的运行规律,如最安全运行位置在哪,工作点在平面位置的变化与其安全性的变化规律。
传统配电网的安全运行最佳点是原点,即不带负荷的点,然而,有源配电网的原点不是其安全运行的最佳点。如图1所示,显而易见,原点距灰色线的安全运行界限并非最长。

图2TQ-DSSR最安全点分析
图2 中,取左下角点O′(0,-0.4),再取点O″。工作点从点O′运行至点O″,PDG,3变小、PL,2变大。O′的安全性可由dO′1和dO′2衡量,O″的安全性由dO″1和dO″2衡量。
由图2可知,dO″1<dO′1,dO″2<dO′2,故O″安全性不如O′。因此,有源配电网的安全运行点是DG满发、负荷空载的运行点[9]。
安全性理论不仅适用于传统配电网,也同样适用于有源配电网。安全性单调减性是指运行安全性随着负荷变大而降低[10]。
4 结语
本文通过提出TQ-DSSR模型,证明了有源配电网和潮流有反向关系,为深入探究微网、储能打下了坚实基础。
通过研究TQ-DSSR的平面运行图,可总结出TQ-DSSR有如下几个特点:
(1)与传统的配电网相比,TQ-DSSR已经从第Ⅰ象限延伸扩展为任一象限。
(2)TQ-DSSR运行平面可能是五边形、梯形、矩形或者三角形。
(3)有源配电网的安全运行点是DG满发、负荷空载的运行点。
(4)安全性理论不仅适用于传统配电网,也同样适用于有源配电网。安全性单调减性是指运行安全性随着负荷变大而降低。

