商榷2018年高考题中表述欠严谨的20道题
北京丰台二中 (邮编:100071)
一年一度的高考是考生、老师、家长、学校乃至全社会关注的重点话题.2018年的高考已尘埃落定,笔者作为一名高中数学老师,也抓紧时间认真钻研了本年度的高考数学真题(文理共计13套,其中上海、浙江文、理同卷,江苏文、理除附加题外同卷),发现了它们有试题常规(多考计算)、情景新颖、杜绝偏怪、难度在降低等特点,这也与新课改之精神、教育乃培养人的活动、数学本来应当是人人能够喜爱的美的科学合拍.但笔者发现有20道高考题在表述上欠严谨:虽然原题不会太影响考生正确答题,但作为高考题的权威性及引用的广泛性,还是要注意表述上的严谨.
笔者发表的文献[1]-[4]分别对2017,2016,2015,2014年的高考题在表述上欠严谨之处也作了商榷.
1 全国卷I
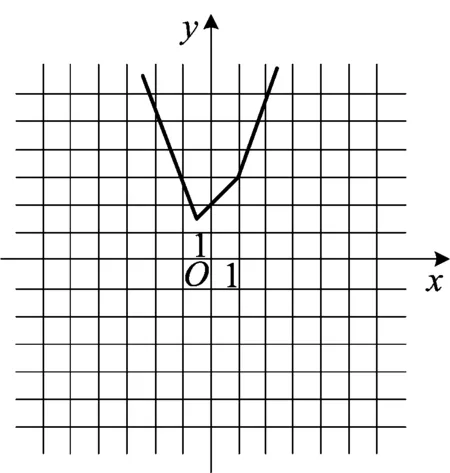
题1(2018年高考全国卷I理科第20题)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p(0 (1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0; (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX; (ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验? 商榷(1)因为现行高中数学教材(人民教育出版社·A版)中没有介绍最大值点的概念(给出了极大值点、极小值点、极值点的概念),所以建议把第(1)问改为“(1)记20件产品中恰有2件不合格品的概率为f(p),若函数f(p)的最大值是f(p0),求p0的所有值;”. (2)建议把这道题目中的“EX”改为“E(X)”,这样才与现行新课标教材“普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社2009年第3版)”一致.在以前的大纲教材“全日制普通高级中学教科书《数学·第三册(选修II)》(2006年人民教育出版社)”中使用的记号是“Eξ,Dξ”,在而后的新课标教材中使用的记号是“E(ξ),D(ξ)”,这是否说明了记号“E(ξ),D(ξ)”更科学呢?笔者认为就是这样的:记号“E(ξ),D(ξ)”的含义类似于函数记号“f(x)”,把“E、D”理解为“对应法则f”更科学. (1)讨论f(x)的单调性; 商榷本题与下面的一道高考题如出一辙(这对于高考有失公平): (1)讨论f(x)的单调性; (2)若f(x)有两个极值点x1和x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线的斜率为k.问:是否存在a,使得k=2-a?若存在,求出a的值;若不存在,请说明理由. 题3(2018年高考全国卷I理科第22题)在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ-3=0. (1)求C2的直角坐标方程; (2)若C1与C2有且仅有三个公共点,求C1的方程. 商榷建议把这道题中的“正半轴”改为“非负半轴”.对2005年高考广东卷第20题也有这种建议. 题4(1)(2018年高考全国卷II文科数学第10题)若f(x)=cosx-sinx在[0,a]是减函数,则a的最大值是 (2)(2018年高考全国卷II理科数学第10题)若f(x)=cosx-sinx在[-a,a]是减函数,则a的最大值是 商榷建议把题4(1)中的“在[0,a]是减函数”改为“在[0,a]上是减函数”;把题4(2)中的“在[-a,a]是减函数”改为“在[-a,a]上是减函数”.否则,语句不通. (1)若a=3,求f(x)的单调区间; (2)证明:f(x)只有一个零点. 商榷建议把题中的“只有一个零点”改为“有且只有一个零点”. 题6(2018年全国卷III文科、理科第23题)设函数f(x)=|2x+1|+|x-1|. (1)在图1中画出y=f(x)的图象; 图1 (2)当x∈[0,+∞)时,f(x)≤ax+b,求a+b的最小值. 图2 (2)由(1)知,当x∈[0,+∞)时,y=f(x)的图象与y轴交点的纵坐标为2,且两部分所在直线斜率的最大值为3,所以当且仅当a≥3且b≥2时,f(x)≤ax+b在[0,+∞)时成立,因此a+b的最小值为5. 商榷建议把以上参考答案末的“f(x)≤ax+b在[0,+∞)成立”改为“f(x)≤ax+b在[0,+∞)时成立”(否则,语句不通). 题7(2018年全国卷III理科第8题)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4) A.0.7 B.0.6 C.0.4 D.0.3 商榷建议把这道题目中的“DX”均改为“D(X)”,理由同题1的商榷(2). 商榷建议把题目中的“在[0,π]的零点个数”改为“在[0,π]上的零点个数”(否则,语句不通). 图3 (1)证明:平面AMD⊥平面BMC; (2)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值. 商榷建议把题目末的“面MAB与面MCD”改为“平面MAB与平面MCD”. 题10(1)(2018年高考北京卷文科第4题)设a、b、c、d是非零实数,则“ad=bc”是“a、b、c、d成等比数列”的( ) (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 (2)设a、b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( ) (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 商榷建议把这两个小题的前三个选项分别改为“(A)充分不必要条件、(B)必要而不充分条件、(C)充要条件”,这样与普通高中课程标准实验教科书《数学·选修2-1·A版·教师教学用书》(人民教育出版社,2007年第2版第11页习题1.2A组第3题的答案一致. 题11(2018年高考北京卷文科、理科第8题)设集合A={(x,y)|x-y≥1,ax+y>4,x-ay≤2},则( ) (A)对任意实数a,(2,1)∈Z (B)对任意实数a,(2,1)∉A (C)当且仅当a<0时,(2,1)∉A 题12(2018年高考北京卷文科第15题)设{an}是等差数列,且a1=ln2,a2+a3=5ln2. (1)求{an}的通项公式; (2)求ea1+ea2+…+ean. 解(1)设等差数列{an}的公差为d. 由a2+a3=5ln2,可得2a1+3d=5ln2. 再由a1=ln2,可得d=ln2.所以an=a1+(n-1)d=nln2. (2)由(1)的答案数列{an}的通项公式为an=nln2,可得ean=enln2=(eln2)n=2n,所以 ea1+ea2+…+ean=eln2+eln22+…+eln2n=2+22+…+2n=2n+1-2. 商榷笔者认为,对于文科试卷的首道解答题,第(2)问有难度:在解答“enln2=(eln2)n=2n”中需要逆用幂的乘方公式(am)n=amn及考生不太熟悉的对数恒等式alogaN=N(且这里是其特例:elnN=N). 建议在第(2)问末给出“参考公式:alogaN=N”. (1)求f(x)的最小正周期; 解可得 商榷笔者认为,官方(北京教育考试院)给出的第(2)问的参考答案: …… 题14(2018年高考北京卷理科第17题)电影公司随机收集了电影的有关数据,经分类整理得到下表: 电影类型第一类第二类第三类第四类第五类第六类电影部数14050300200800510好评率0.40.20.150.250.20.1 好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. 假设所有电影是否获得好评相互独立. (1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率; (3)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等.用“ξk=1”表示第k类电影得到人们喜欢,“ξk=0”表示第k类电影没有得到人们喜欢(k=1,2,3,4,5,6).写出方差Dξ1,Dξ2,Dξ3,Dξ4,Dξ5,Dξ6的大小关系. 商榷(1)建议把这道题目中的两处“电影公司”均改为“某电影公司”. (2)建议把这道题目中的“第一类、第二类、第三类、第四类、第五类、第六类”分别改为“第1类、第2类、第3类、第4类、第5类、第6类”,否则第(3)问中的“第k类电影没有得到人们喜欢(k=1,2,3,4,5,6)”与题设不符. (3)建议把这道题目及其解答中的“Dξ,Dξ1,Dξ2,Dξ3,Dξ4,Dξ5,Dξ6”分别改为“D(ξ),D(ξ1),D(ξ2),D(ξ3),D(ξ4),D(ξ5),D(ξ6)”,理由同题1的商榷(2). (1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间? (2)求该地上班族S的人均通勤时间y2=8x(0≤x≤t,y≥0)的表达式;讨论y2=8x(0≤x≤t,y≥0)的单调性,并说明其实际意义. 商榷建议把题目中的“单日”改为“当日”(因为单日与双日是一对词). 还建议把题目中的“(1)当x在什么范围内时”改为“(1)当且仅当x在什么范围内时”,否则答案不确定:答案可以是(45,100)的任意非空子集. 题16(2018年高考上海卷第21题)给定无穷数列{an},若无穷数列{bn}满足:对任意n∈N*,都有|bn-an|≤1,则称{bn}与{an} “接近”. (1)设{an}是首项为1,公比为n∈N*的等比数列,bn=an+1+1,n∈N*,判断数列{bn}是否与{an}接近,并说明理由; (2)设数列{an}的前四项为:a1=1,a2=2,a3=4,a4=8,{bn}是一个与{an}接近的数列,记集合M={x|x=bi,i=1,2,3,4},求M中元素的个数m; (3)已知{an}是公差为d的等差数列,若存在数列{bn}满足:{bn}与{an}接近,且在b2-b1,b3-b2,…,b201-b200中至少有100个为正数,求d的取值范围. 商榷建议把题目中没有打引号的“接近”(共3处)带引号的“接近”,因为两者的含义不同. 商榷建议把题中的“设鸡翁,鸡母,鸡雏个数”改为“设鸡翁,鸡母,鸡雏只数”. 商榷建议把题中的“以AB为直径的圆C”改为“以AB为直径的圆(其圆心为点C)”.因为“圆C”中的C指的是曲线(即圆)而不是点(即圆心). 题19(2018年高考江苏卷第14题)已知集合A={x|x=2n-1,n∈N*},B={x|x=2n,n∈N*}.将A∪B的所有元素从小到大依次排列构成一个数列{an}.记Sn为数列{an}的前n项和,则使得Sn>12an+1成立的n的最小值为______. 商榷建议把题中的“{x|x=2n-1,n∈N*}”改为“{2n-1|n∈N*}”,“{x|x=2n,n∈N*}”改为“{2n|n∈N*}”,“记Sn为数列{an}的前n项和”改为“记Sm为数列{an}的前m项和”. 前两处改动的目的是简洁(数学的表述应当尽可能简洁),对第三处改动的原因说明如下: 题中的叙述“记Sn为数列{an}的前n项和”很流行(教材也是这样叙述的),但这里三个“n”含义不同: 第一个“n”和第三个“n”的含义相同(表示同一个数或同一个变量),但它们与第三个“n”的含义不同:“{an}”中的“n”指数列{an}的第n项(即通项)an中的变量;即使第一个“n”和第三个“n”均表示同一个变量时,与“{an}”中的变量“n”含义也不同(可取不同的值). 因而,第三处的改动是必须的(同一句话中的三个“n”表示的含义不全相同,是多么的匪夷所思呀).也建议这种流行的错误叙述(包括教材)尽早更改过来. 题20(2018年高考江苏卷第20题)设{an}是首项为a1,公差为d的等差数列,{bn}是首项为b1,公比为q的等比数列. (1)设a1=0,b1=1,q=2,若|an-bn|≤b1对n=1,2,3,4均成立,求d的取值范围;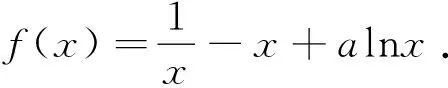
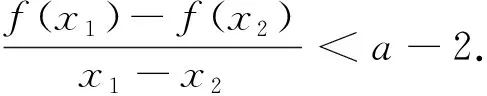
2 全国卷II
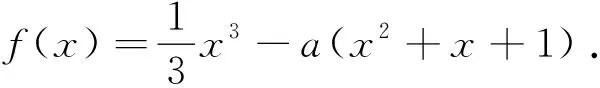
3 全国卷III
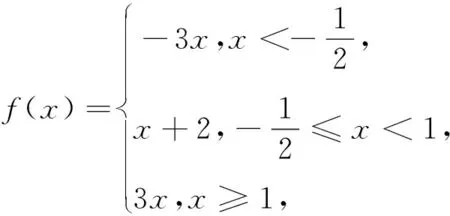



4 北京卷
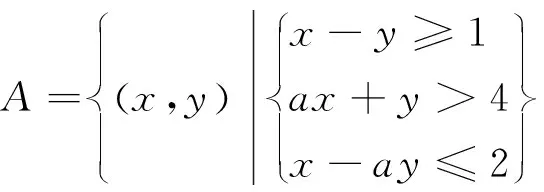
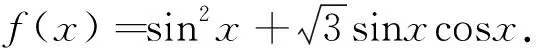
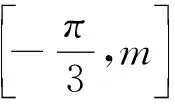


5 上海卷
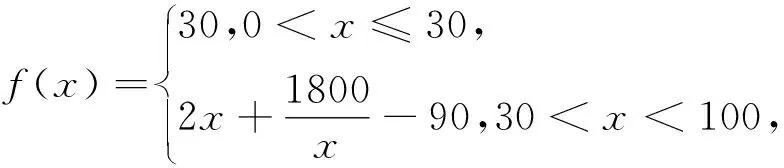
6 浙江卷
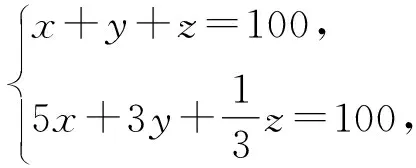
7 江苏卷