中药自动抓药系统设计与验证

鱼先锋

（商洛学院数学与计算机应用学院 商洛 726000）

1 引言

据中国产业调研网发布的2016年版中国中医医院市场调研与发展趋势预测报告显示，近年来，党和政府高度重视中医药事业发展，中医医院办院规模扩大，但是，中医医院也存在中医药房人工抓药效率低下，药品称量不够精确等问题，影响了中医医院的持续健康发展。为摆脱中药传统落后的配药模式，自动配药系统的研制是十分迫切的。中药的颗粒化，使中药自动配药系统中取药的定量化和精确化成为可能［1～4］。70年代末曾风行全国的所谓“电子配药机”，到80年代中期基本在中药房消失了。原因是对“电子配药机”上所用的原始生药实现定量和输送都极为困难，而且由于科技含量低，上层药斗加料人员与下层操作人员无法进行信息沟通，机器经常出现“空放”现象［5］。对此，文章拟设计一个中药自动抓药系统模型，高效自动地为患者抓药且避免了机器出现“空放”现象。这将大大提高中药房工作效率，提升中医院服务质量。形式化验证是在对系统进行规约的基础上，分析系统是否具有所期望的性质。模型检测［6～12］是当前最流行的一种形式化验证方法。文章用模型检测的方法对中药抓药系统进行形式化验证，以保证系统设计合理，安全可靠。

2 系统建模

2.1 系统描述

一个中药抓药系统如图1，可描述为

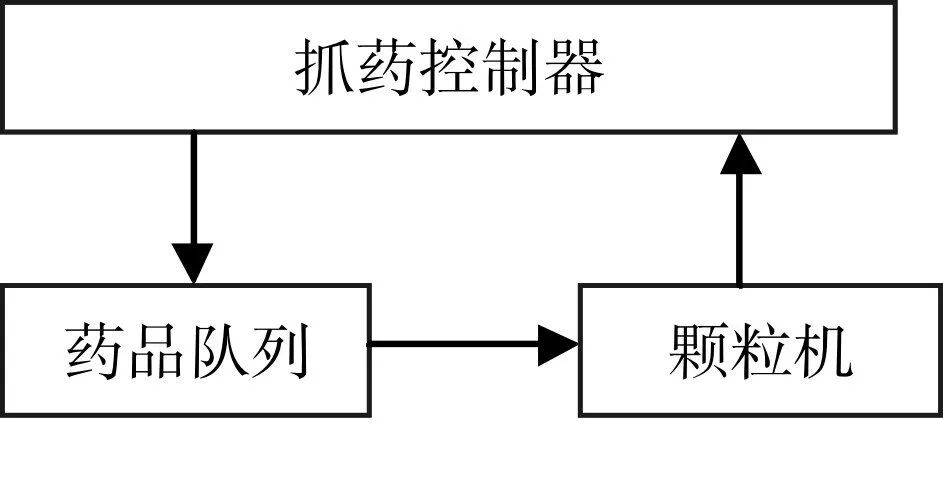
图1 中药抓药系统

中药自动抓药系统有三部分构成：药品队列，颗粒机，抓药控制器。

1）药品队列是控制器从门诊医生写入数据库的药方中读出来的药品名称、剂量等信息，并按照每种药品的响应比排成有序序列。

2）颗粒机是用来自动抓药的，在抓药控制器控制下在颗粒机闲暇时从药品队列中读取当前响应比最高的药品信息入颗粒机，根据药品名选择中药，并按照剂量选择颗粒桶的多少，最终将颗粒桶中的中药倒入中药袋。颗粒桶是封装各类药品的最小容器单元，每个颗粒桶容纳重量确定的一种药品颗粒。颗粒机还要计算每种药品在药柜的存放地址，以及药品颗粒桶数目的变化，在药品不足时向控制器发送加药信息。

3）抓药控制器控制协调抓药系统的运转。计算药方上各种药品的响应比，将药品排成有序队列；计算每种药品的颗粒桶数。控制颗粒机按照药品名称在药柜中找到药品，根据当前药品颗粒数控制颗粒机抓药。在当前药品抓完之后，从队列中选择下一种药品抓药；直至药品队列中的药品全部抓好，变转而抓下一个药方上的药，不断循环工作。

中药自动抓药系统要合理、安全地实现自动抓药必须满足以下性质：

1）安全性：颗粒机是临界资源，在任意时刻只能有一种药品占用颗粒机自动抓药；

2）活性：所有药方上的药，最终都将配齐；

3）无阻性：每一中药方上的药都可以在计算出其响应比后进入药品队列等待颗粒机抓药。

安全性是为了保证精准抓药。活性一方面防止出现不合理的空转，也就是队列有药要抓并且系统时刻已经超过它们等待时间的话一定有药被抓取；另一方面活性也体现了公平性，即所有药都将抓取。无阻性也明显的体现了公平性，无阻性是活性和安全性的基础。

2.2 系统的形式化建模

我们将考虑不同药品封装颗粒桶难度σ，药品剂量m等因素定义公平合理的响应比t；中药抓药系统进行形式化建模，规约成Kripke结构。并将系统的安全性、活性和无阻性形式化规约成CTL或LTL公式，以便进行形式化验证，证明系统合理性。

定义1 中药自动抓药系统A为一个八元组A=(AP,L,N,Q,q0,δ,F,，其中：

2）赋值集L={0,w,r,1}，0表示此中药未排进抓药对列即未就绪，w表示中药在队列等待被抓取，r表示此中药正在自动抓取，1表示次中药已经抓好；

3）Q是有穷状态集合，Q⊂LAP，即 AP到 L的部分映射；∀q∈Q,pi∈AP,li∈中药 pi的值为li，记表示再记li为qi；

4）N为自然数集合，表示系统时间；

5）q0∈Q态，表示这批中药都未就绪；

7）时序控制阵定义为

这里i=1,…,n对应不同的中药。

（1）T1i表示第i味中药被自动抓取进入等待队列时刻，T1i=t0+t0i⋅fi.eρi。其中t0表示第i味中药检索其在药柜中颗粒桶库存状态 fi所需时间，我们认为检索每种中药 fi所需时间相同。fi∈{0 ,1}，fi=1表示第i味中药的库存颗粒桶数Δmi少于当前药方上的需求颗粒桶数mi（Δmi＜mi）；fi=0 对应 Δmi≥mi。 t0i是每次在药柜给第i味中药上柜其规定药量所需的基准时间。 ρi≥0表征第i味中药的封装难度，它与药品种类有关，若药品颗粒桶是提前封装好的话ρi=0。e为宇宙常数；

（2）T2i表示第i味中药预计自动抓取时长，表征第i味中药的抓药难度，它与药品在药柜中的位置有关，若不考虑药品在药柜位置对取药的影响则可规定

qi=r时，正在抓取中药 pi其响应比定义成+∞，其他中药不能进入抓药程序。qi=0时，中药pi尚未进入等待序列即未就绪，其响应比定义成-∞。qi=1时，中药 pi抓取结束其响应比定义成-∞，释放了抓药系统临界资源。与t-T1i正相关刻画了等待时间t-T1i越长响应比越高体现了公平性，负相关刻画了预计抓药时长越长响应比越小，这体现了贪心算法的思想，在最短时间内抓尽可能多种类的中药；

（4）T4i表示第i味中药开始被处理时刻，初始化为 +∞ ，若在系统时间 t时 ∃s,q∈Q，使得δ(s,t)=q且 si=w,qi=r则T4i=t。

8）中药自动抓药函数为映射δ:Q×N→Q系统时间t时有δ(s,t)=q，则

（1）qi=w ，当 ∀si=0，T1i≤t；

（2）qi=1，当 ∃si=r使得T2i≤t-T4i；

（5）qi=si，其它情况。

下面将定义1建立的中药抓药系统模型诱导成一个Kripke结构为系统做模型检测准备。

定义2 一个中药抓药系统A对应一个Kripke结构 A=(AP,S,S0,R,Ls)，其中：

1）AP是中药之集，AF={p1,…,pn}；

2）S是有穷状态之集，S=Q；

3）s0∈S为初始状态，s0=q0；

4） R⊆S×S 为 状 态 转 移 关 系 ，∀(s,s′)∈S×S ，(s,s′)∈R ，当且仅当 (s,s′)∈Q×Q ，∃t=N ，使得 δ(s,t)=s′；

5）Ls:S→2L×AP为状态标识函数，∀s∈S，

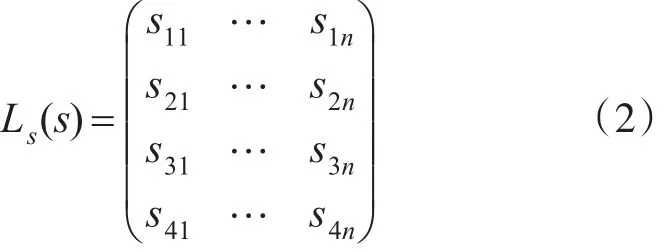
（1）s1j表示第 j个中药在该状态取值为“0”的真值(0|1)；

（2）s2j表示第 j个中药在该状态取值为“w”的真值(0|1)；

（3）s3j表示第 j个中药在该状态取值为“r”的真值(0|1)；

（4）s4j表示第 j个中药在该状态取值为“1”的真值(0|1)。

根据定义2对Ls的定义，∀si∈S计算 Ls(si)，实际上是把多值向量编码成二值矩阵。

定义3 一个中药自动抓药系统A是安全合理的当且仅当A满足以下3个LTL公式：

根据LTL公式语法语义规定［13］，定义3对中药自动抓药系统安全性、活性、无阻性的刻画是合理的。 A满足 f1,f2,f3,f4，记作 A|=f1˄f2˄f3。

定义4 LTL公式 f是中药自动抓药系统A性质约束公式，映射Sat(f)：f→2S，称为满足 f的A的状态之集。 ∀s∈S, s∈Sat(f), 当且仅当s|=f。若初始状态s0∈Sat(f)，则称A|=f。

3 模型检测

3.1 中药自动抓药系统模型的模型检测算法

有了计算模型与性质约束公式就可以进行互斥模型的形式化验证。选择合适的模型检测算法（最常用的有标号法［14］，不动点模型检测算法［6，15］等）计算 A|=f1˄f2˄f3；结果为真则模型是合理的。否则模型不合理给出反例路径对模型做进一步的精化改进。

定理1（不动点刻画）定义3给出性质约束公式可以通过求以下函数不动点求得各公式的可满足状态，

1）AGφ=vZ⋅(φ˄AX(Z))；

2） A(φ1∪ φ2)= μZ⋅(φ2˅(φ ˄(AX(Z))))。

证明 有关式（1），（2）合理性证明详见文献［16］。

下面给出基于不动点理论的中药自动抓药系统模型的模型检测算法。

输入：中药自动抓药系统模型A，性质公式f1,f2,f3；

输出：不动点，即满足A的状态集合。

计算：

1）用分治策略验证各个中药 p1,p2,…,pn是否满足合理性约束，最后确定中药自动抓药系统模型A是否满足合理性约束；

2）迭代求不动点过程中各公式看作满足它的状态之集；

3）逻辑运算˄, ˅,¬对应集合运算∩,∪,-；

4）计算结果如果，s0属于不动点则模型满足性质约束，反之不满足。

定理2（算法复杂度）［17］不动点模型检测算法的复杂度为O( ||f⋅(||S+ ||R))，其中 ||f是性质公式f子表达式个数， ||S是状态数， ||R是状态迁移数。

3.2 中药自动抓药系统模型的模型检测实例

下面用中药自动抓药系统A抓取治低血压的中药方上3味药的模型检测实例。药方与初始化信息如表1所示。认为每种药品颗粒桶封装10g该药品。

表1 药方与初始化信息

模型建立的主要工作在于计算时序控制矩阵，并根据时序控制矩阵计算中药抓药系统状态的迁移状况。

1）根据 T1i=t0+t0i⋅fi.eρi计算等待时间。认为搜索 fi所需时间为“1”即t0=1则，T11=1+2×0×1×e=1，T12=1+1×1×1×e0=2，T13=1+1×0×1×e2=1。

3）根据定义1中式（1）计算系统初始时刻“0”时刻响应比得到时序控制阵

进而可以计算任意系统时刻的时序控制矩阵。

4）根据定义1第8）中药自动抓药函数ε(s,t)=q的定义计算中药自动抓药系统状态变化，为表2所示（连续两个以上同样状态只列出了第一个和最后一个）。

表2 状态变化表

状态转移图如图1所示。

根据定义2计算图2生成的Kripke结构如图3所示。其中，

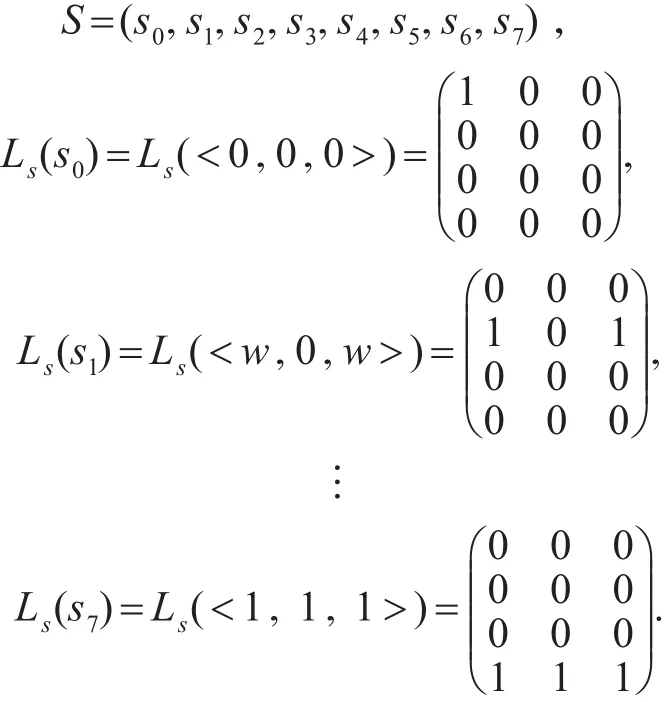
图2 表2对应状态转移图

图3 图2对应的Kripke结构图

5）系统合理性公式为 f1˄f2˄f3，其中，

6）系统不动点模型检测如下：

（1）验证系统安全性

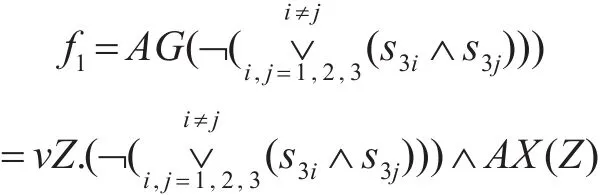
最大不动点的计算如下：

显然 τ1(S)=S为最大不动点；因为s0∈S所以系统满足安全性约束。

（2）验证系统活性

f21=A(Fs21∪s41)=μZ.(s41˅((Fs21)˄AX(Z))) 的最小不动点计算如下：

显然 τ5(φ)=S 为 f21=AF(s21∪s41)的最小不动点；因为s0∈S所以中药 p1在系统抓取过程中满足活性约束。如法炮制可以验证中药 p2,p3在系统抓取过程中满足活性约束。所以就验证了系统满足活性要求。

（3）验证系统无阻性

f31=A(Ture∪s21)，f32=A(Ture∪s22)，

f31=A(Ture∪s23)。

f31=A(Ture∪s21)=μZ.(s21˅(Ture˄AX(Z))) 的最小不动点计算如下：

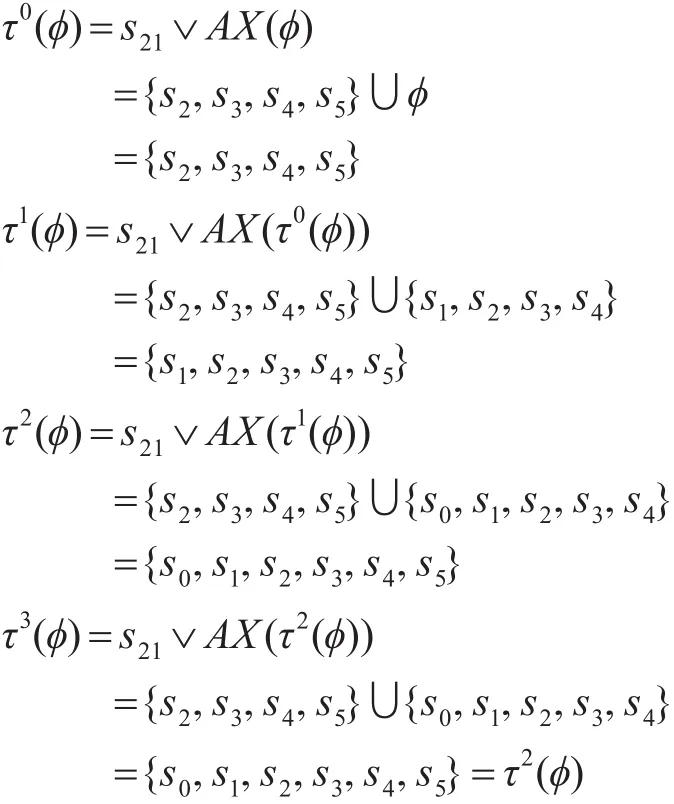
显然τ2(φ)={s0,s1,s2,s3,s4,s5}为 f31=A(Ture∪s21)的最小不动点。

因为 s0∈{s0,s1,s2,s3,s4,s5}所以中药 p1在系统抓取过程中满足无阻性约束。如法炮制可以验证中药 p2,p3在系统抓取过程中满足无阻性约束。所以就验证了系统满足无阻性约束。

综合（1），（2），（3）就可以验证实例中中药自动抓药系统满足安全性、活性和无阻性；故而系统是安全合理的。

4 结语

文章设计了一个中药自动抓药系统模型A=(AP,L,N,Q,q0,δ,F,（定义 1）。定义了时序控制矩阵存储计算系统的响应比。定义了合理的状态迁移函数，刻画系统运行状态。实现系统自动、高效、精准抓药。将系统规约到Kripke结构（定义2），定义了系统安全性、活性、无阻性等约束性质保证系统公平、合理不“空转”；并将这些性质抽象成LTL公式（定义3）。给出了系统基于不动点的模型检测算法（3.1）。在系统规约得到的Kripke结构上形式化验证系统安全性、活性、无阻性。分析了算法的复杂度（定理2）。最后给出了系统的一个模型检测实例，证明系统安全、合理。