数学游戏与数学思想方法例谈

张新春

数学思想方法作为“将具体的数学知识忘掉后剩下的东西”，对学生的影响是巨大的。它使学生得到基本数学思想方法的熏陶，以适应未来社会生活和继续学习的需要；使学生领略数学探索、研究以及数学应用的基本方法，从而能从数学的角度、运用数学的思维方式去观察、分析现实生活中的事物，并会数学地解决问题。这些都应该是数学课程的重要目标。

按照《辞海》的说法，游戏是文化娱乐的一种，有发展智力的游戏和发展体力的游戏。前者包括文字游戏、图画游戏、数字游戏等，习惯称为“智力游戏”。数学游戏显然是智力游戏，而且是蕴含着数学知识和数学思想方法的智力游戏。研究这些数学游戏，有利于学生在生动活泼的过程中体会一些基本的数学思想方法。本文以两个数学游戏为例，从数学思想方法的角度作出分析。

一、“10根火柴棒”游戏

【游戏介绍】

这是一个单人智力游戏。如图1，有10根火柴棒，一字排开。我们的目标是移动这10根火柴棒，使之两两一组，分成5组。

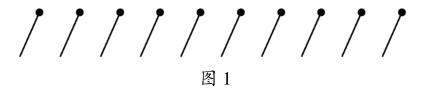
移动的规则是：可以拿起任何一根火柴棒，放到与之相隔两根火柴棒的火柴棒上，从而形成一组。图2即表明了一种合法移动。（虚线位置表示当次移动之前被移动火柴棒所在位置，下同）

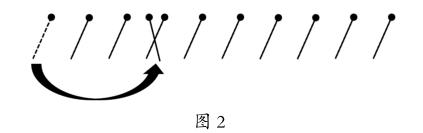
在上面第一次移动的基础上，图3表明了一种合法移动。

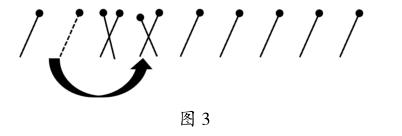
以上两次移动表明了游戏规则。

移动到此，我们可以发现，已经没有办法完成游戏任务了。事实上，此时已经不可能有某一根火柴棒和左边的第一根配成一组了。

【分析】

我们可以反复尝试，最终也能够找到方法。若从数学思想方法的角度思考，则可以考虑如下思路。

思路一：化繁为简

化繁为简、以退为进的思路，在数学问题解决中常用。

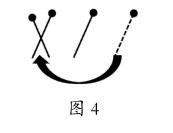
10根火柴棒配成5組，问题比较复杂，我们可以从最简单的情况研究。显然，要考虑“隔两根”的条件，至少应该从4根火柴棒的情况开始。我们很容易发现，4根火柴棒没有可能按规定配成两组。事实上，面对4根火柴棒，我们第一步只能把最左边的一根移到最右边，或者把最右边的一根移到最左边。接下来就没有办法操作了（如图4所示）。

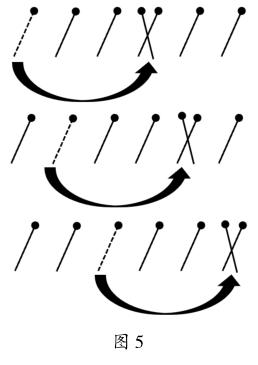
我们来考虑6根火柴棒的情况。首次移动的方法只有三种（如图5所示）。（说明：这三种方法都是将左边的火柴棒往右边移。当然，相应地，还有将右边的火柴棒往左边移的方法。但由对称性可知，如果从左边往右边移不能成功，那么从右边往左边移也不能成功。而考虑对称性本身就是很重要的数学方法）不难判断，无论是三种情况中的哪一种，都无法继续完成游戏任务。

再考虑8根火柴棒的情况。通过一一列举（移左边第一、第二、第三、第四根），可以发现一种可行的方案。图6是前面两步。

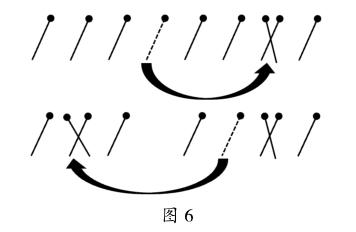
这两步之后，变成如下的局面（如图7所示），接下来的操作就很显然了。

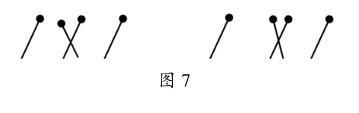
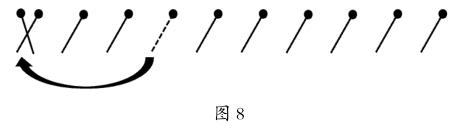
我们已经发现了将8根火柴棒按要求配成4组的方式，但要解决的问题是10根火柴棒配成5组。于是，我们要做的工作是如何将10根火柴棒的问题转化成8根火柴棒的问题。转化本身也是非常重要的思想方法。事实上，完成这种转化的方法很简单。只要按图8所示，将第4根移过来和第1根组成一组，问题就变成8根火柴棒配成4组，而这个问题我们前面已经解决了。

思路二：倒推

有这样一些问题，它们涉及一个过程，过程的起点是清楚的，过程的结果也是清楚的，要寻找的就是过程本身。最明显的例子就是走迷宫———起点清楚，终点清楚，就是要寻找起点到终点的路。解决这样的问题，我们很容易想到的方法是倒推，从终点出发，努力回到起点，路就找着了。

这个10根火柴棒的游戏也和走迷宫一样。我们可以用倒推的方法解决问题。一个倒推的过程如图9所示。

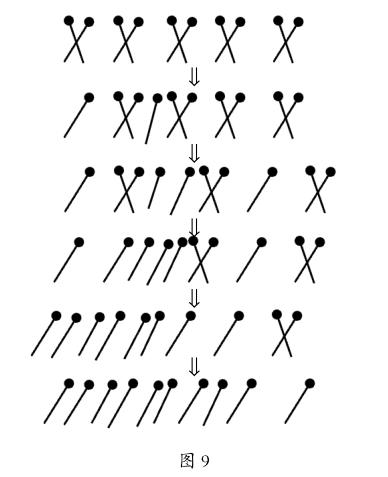
将以上过程逆转过来，即是将10根火柴棒配成5组的方案。事实上，上述倒推的过程几乎没有任何难度，甚至无需过多思考，见招拆招就能解决。而且方案不止一种。

二、“取棋子”游戏

【游戏介绍】

这是一个双人对策游戏。有黑棋8枚，白棋6枚。甲乙两人轮流取棋，轮到某人取棋时，合法的取法分两类：

第一类，只取一种颜色，则棋子的颜色任意，取的棋子的数量任意。不能不取。

第二类，取两种颜色的棋子，则要求两种颜色的棋子取一样多。在此基础上取棋子的数量任意，不能不取。

取得最后一枚棋子的人获胜。

【分析】

思路：数形结合

游戏开始时有黑棋8枚，白棋6枚。游戏结束时，黑棋白棋均为0枚。这中间的每一个局面，都由一对有序数对表示。这样的视角，就使我们有了用数形结合的办法解决这个问题的基础。

现在，我们将这个游戏及其规则完整地转化为一个图形问题。