斑块区域环境中传染病模型全局稳定性研究

李艳秋，王 楠

(1.吉林工程技术师范学院应用理学院，吉林长春 130052；2.吉林工程技术师范学院数据分析创新团队，吉林长春 130052)

1 研究背景

在种群动力学文献中，多采用连续反应扩散系统和离散斑块区域模型来描述种群扩散的空间不均匀性[1].虽然反应扩散系统适合于随机的空间扩散，但斑块区域模型通常用于描述区域之间的定向运动，当传染病模型中空间不均匀性时，种群运动使得传染病可以在国家和地区之间，或在城市之间发生传播.

斑块区域环境中的离散空间传染病模型是非线性微分方程中的热点问题，其全局动力系统的建立是一个数学难题.Arino和Van den Driessche建立了n座城市之间传染病模型，研究了城市间旅游对城市传染病空间扩散的影响，推导出了基本再生数R0，并进行了数值模拟，结果表明R0<1时疾病消失，R0>1时传染病成为地方病[2].王稳地等研究了一个具有双线性关联的n斑块SIS模型；在每个区域上的可疑和传染性个体具有相同的扩散速率的情况下，证明了如果R0<1，无病平衡点是全局渐近稳定.同时还证明如果R0>1，系统是一致持久的和地方病平衡点的存在性.在同样的假设下，易感和传染性个体的传播速率是相同的，n斑块SIS模型可以被简化为单调系统，利用单调动力系统理论，证明了当R0>1时，局部平衡的唯一性和全局稳定性[3].在许多斑块区域传染病模型中，当R0>1时，地方病平衡点的唯一性和全局稳定性没有得到解决，利用Lyapunov函数方法研究在斑块区域环境中的传染病模型的全局稳定性相关工作很少.

近年来，许多文献采用了图论方法对大规模耦合系统的全局Lyapunov函数的构造进行了系统化[4-6].该方法已被成功地应用于求解多群传染病模型特有平衡点的全局稳定性问题，并解决了斑块区域环境中捕食者-食饵模型的正平衡问题.本文利用新的方法来研究具有n个区域的传染病模型的局部平衡的全局稳定性.考虑在斑块区域环境中的双线性传染病的SIR传染病模型：

(1.1)

由于变量Ri没有出现在(1.1)的前两个方程中，所以可以首先研究简化系统.

本文将讨论如下系统(1.2)，并假设初始条件Si(0)≥0,Ii(0)≥0.

(1.2)

2 初步结果

2.1 无病平衡点

为了找到(1.2)的无病平衡点，考虑以下线性系统：

(2.1)

矩阵形式表示为DS=Λ.其中，

由于D的所有非对角线元素是非正的，并且D的每个列中的元素和是正的，因此D是非奇异M-矩阵,D-1≥0[7].对于∀i，Si(0)≥0，线性系统(2.1)具有唯一的正解S0.

性质1 系统(1.2)存在唯一的无病平衡点P0.

2.2 可行区域

因此(1.2)的可行区域选择为：

(2.2)

2.3 基本再生数

令

(2.3)

(2.4)

参照van den Driessche[2]的方法，计算出基本再生数为R0=ρ(FV-1).其中，ρ表示矩阵的谱半径，FV-1是再生矩阵.

依据文献[8]中定理2，得到如下结论：

性质2 系统(1.2)的无病平衡点P0，当R0<1时局部渐近稳定；当R0>1时不稳定.

2.4 其它边界平衡点

定理1 假设B=(bij)是不可约的，那么在∂Γ中除了P0外无其它边界平衡点.

证明 规定对任意i,有Ii=0蕴含着对任意j,有Ij=0.

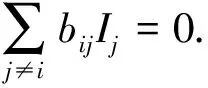
由于B是不可约的，则存在有序对的序列{(i,r1),(r1,r2),…,(rm,j)},使得：

bir1>0,br1r2>0,…,brmj>0,1≤rk≤n,k=1,2,…,m.

因此，

Ir1=0,Ir2=0,…,Irm=0,Ij=0，i=1,2,…,n.

即，∀j,Ii=0.

根据性质1得到，方程在边界∂Γ存在唯一的平衡点P0.

3 无病平衡点P0的全局稳定性

本节将证明当R0≤1时无病平衡点P0是全局渐近稳定性的.

定理2 如果R0≤1，传递矩阵B=(bij)是不可约阵或是零阵，那么在Γ中P0是全局渐近稳定的.

证明 证明传递矩阵B=(bij)是不可约阵的情况.B=0的情况类似可证.

设F,V分别由(2.3)和(2.4)中给出.V的所有非对角线项都是非正的，且每一列之和为正，因而V是一个非奇异的M-矩阵.假设B是不可约的，则V-1>0也是不可约的.根据Perron-Frobenouse定理[7]，非负不可约矩阵V-1F存在一个正左特征向量(ω1,ω2,…,ωn),对应特征值为ρ(V-1F).

因此，L是系统(1.2)的李雅普诺夫函数.

利用(2.1)式可得,Ii=0(对于i=1,2,…,n).因此，如果L′=0，那么Ii=0.

4 局部平衡点的唯一性和全局稳定性

在假设R0>1条件下，利用图论方法[5,6,10]推导局部平衡点是唯一的且全局渐近稳定的充分条件.

需要注意的是，对于x>0，恒有1-x+lnx≤0(等式成立当且仅当x=1).根据系统(1.2)对Vi微分.

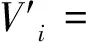
(4.1)

附录：记(G,W)是一个n≥2的加权二坐标向量，W=(wij)是权重矩阵.如果从顶点j到顶点i的有向弧(j,i)存在，则权重wij>0；否则wij=0.设Ti为(G,W)根在顶点i的所有生成树集合，对于t∈Ti，以W(t)表示t的权重，是t的所有弧上的权值的乘积.

若

(A.1)

(A.2)

如果W=(wij)是不可约阵，那么对于所有i，有ci>0[6].