基于FSVM算法的TCD医疗数据分类
王志远,吴成浩,王 正,张亚峰,王 佳
(北京送变电有限公司,北京 102401)
0 引言
经颅多普勒超声(TCD)是一种无创性检查脑血管疾病的方法,广泛用于早期筛查和诊断脑卒中患者的颅内动脉疾病[1]。通过对TCD数据的研究和分析,可以有效帮助临床医生诊断疾病,提高诊断质量和效率。支持向量机(Support Vector Machine,SVM)是一种基于统计理论的机器学习方法。它具有很好的泛化能力,在面对非线性、小样本和高维数据时具有很好的实用性。在这种情况下,它表现出良好的分类效果,被广泛用于各种医疗数据的处理。然而,SVM的固有机制决定了它对训练样本的噪声点特别敏感。这些噪声和异常都会导致SVM的分类不佳。同时,大部分TCD医学数据在分类过程中都是正面和负面的。在不平衡的情况下,少数类(正类)通常包含大量的信息,但支持向量机对少数类的识别较差,导致分类性能差。其次支持向量机对噪声和孤立点敏感的特性,也大大影响最终的分类结果。
针对以上问题,文献[2]首先提出用模糊支持向量机(Fuzzy Support Vector Machine,FSVM)为训练样本提供不同的权重。文献[3]根据正负样本数目的比值来对惩罚因子进行设置,有效解决了样本分布不均匀的问题。文献[4]设置参数,动态调整选取训练样本的范围,同时对样本进行预处理,有效地避免了孤立点对最优的分类超平面所造成的影响。文献[5]提出了一种基于不同惩罚因子的方法(Different Error Costs,DEC),该算法以正负样本数目的比值作为平衡因子,并据此调整数据集的不平衡性。这种方法没有考虑到样本点周围的疏密性对分类超平面的影响。文献[6]提出了一个双边加权模糊支持向量机,并应用到信用评分领域。文献[7]通过预选有效候选支持向量缩减训练样本集规模,提高训练效率。文献[8]提出了模糊支持向量机模式分类改进算法并用于动脉硬化病分类。本文提出一种新的FSVM算法,考虑到每个样本邻近区域的样本分布状况以及样本集的不平衡程度,设定控制值灵活的控制样本集的范围,减弱野值点的影响并有效突出支持向量的作用,提高了识别准确率。
1 模糊支持向量机

s.t.yi[w·φ(xi)+b]-1+ξi≥0,
ξi≥0,i=1,2,3,…,n
(1)
式中C+,C-为常数,分别代表正负类样本的惩罚因子。为求解式(1),通过拉格朗日函数,得出其对偶规划为:
maxw(α)=
(2)
约束条件为:
(3)
式(2)中k(xi,xj)=φ(xi)φ(xi)T为核函数。传统支持向量机分类方法如图1所示,模糊支持向量机相比于传统SVM的优势在于能够根据样本点对分类超平面贡献程度给样本赋予不同权重,实现分类超平面的优化。
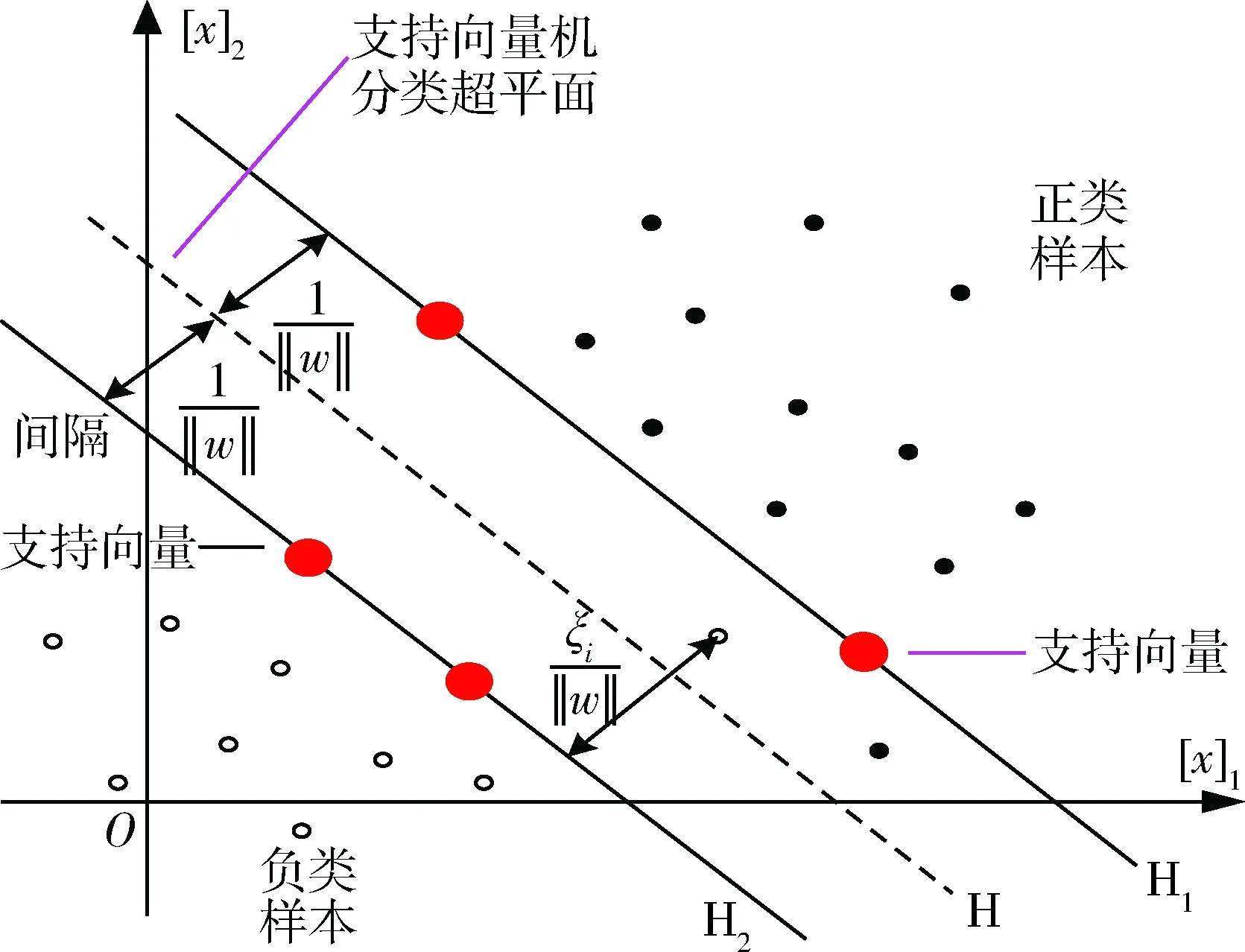
图1 SVM分类表示图
2 面向TCD医疗数据集的FSVM隶属度设计
2.1 传统隶属度函数设计方法
传统的隶属函数旨在减少异常值和噪声点对最优分类器超平面的影响,它们中的大多数都是根据样本到类内中心的距离来设计的。基本的设计思想是根据样本到类中心距离的远近来进行权值赋予。随着距离的增加,赋予的权重值变小,这种对样本赋予权重的方法是不准确的,因为它忽略了远离类中心的支持向量的影响,如图2所示,支持向量(图中粗体部分)由于距类别中心的距离较远而被赋予较小的权重,使得分类超平面偏离最优超平面,并且由于距类内中心的距离不同,这些对分类超平面贡献一样的支持向量却被赋予了不一样的权重,所以传统的隶属函数设计有其不足之处。

图2 根据样本到类中心的距离进行隶属度函数设计
2.2 改进的模糊隶属度函数设计方法
首先对支持向量进行预选,根据决策中起决定性作用的支持向量通常位于类边界的原则,相对于同类样本,其距离类中心是相对比较远的。其次通过对过两类中心的且与两类类中心连线垂直的平面做平移,平移距离为本类样本点到类中心的最远距离,也就是最大半径值,设置灵活控制因子进行调整,排除野值和噪声点,最后达到有效对样本权值实现精确赋予优化分类超平面的作用。
记正负类训练样本类中心分别为c1、c2。以w=c1-c2为法向量,分别求解过c1、c2的两个类内超平面:
(4)

(5)
此时,正负类中样本点到另一类类内超平面距离为:
(6)
正负类中样本点到平移过后的类内超平面距离:
(7)
计算两类类中心的距离:
(8)
基于样本到过样本类中心超平面隶属度函数计算公式为:
(9)
(10)
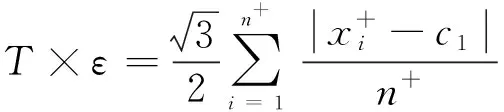

图3 隶属度函数设计方法示意图
由以上分析可以看出,本文所提出的模糊隶属度函数设计方法具有如下优势:
(1)通过灵活设置半径控制因子可将样本进行预处理,优化样本集,给噪声点赋予较小的隶属度值,使其不影响分类结果。
(2)将正类样本点到过平移后的负类中心超平面的距离bi+与T值进行比较,可以将实线圆以内的样本点分为两部分,能够对每个样本点进行精确赋值,使得支持向量被赋予更大的权值,减弱非支持向量的作用,突出支持向量对分类超平面的贡献。
(3)通过求样本到过类中心超平面的距离对其进行权值赋予的方式大大解决了传统样本到类中心距离设计方法导致的样本赋值不准确的问题。
3 实验与结果分析
3.1 评价指标
对于非平衡情感数据集,本文采用不平衡数据学习中的Se、Sp、Gm来评价分类效果[10],其定义为:
(11)
其中,TP、FN、TN、FP分别代表分类正确的正样本、分类错误的负类样本、分类正确的负类样本以及分类错误的正类样本的个数,Se、Sp分别代表分类器正确预测正负类样本的比率,但很多时候具有高Se的分类器不一定有高的Sp,故引入几何均值Gm来评价分类器性能,Gm越大,分类效果越好。
3.2 TCD数据集实验
本实验运行在单机Windows 7系统上,机器配置为:Intel(R) Core(TM) i5-3570CPU @ 3.40 GHz。算法采用MATLAB软件进行测试。先将数据做归一化处理,然后选择2/3的数据作为训练样本,剩下的1/3数据用作测试样本。
本文采用高斯径向基核函数作为分类器核函数,并将本文隶属度设计方法RFSVM与文献[7]中的OFSVM算法以及文献[8]中ZFSVM隶属度设计方法做比较,将其应用于TCD医疗数据。收集和整理1 572例来自人民医院的经颅多普勒超声数据,其中包括1 226 例正常人,91例斑块患者以及255例狭窄患者,很显然患者数据与正常人数据之间存在着不平衡关系,其原始数据波形如图4~图6所示。
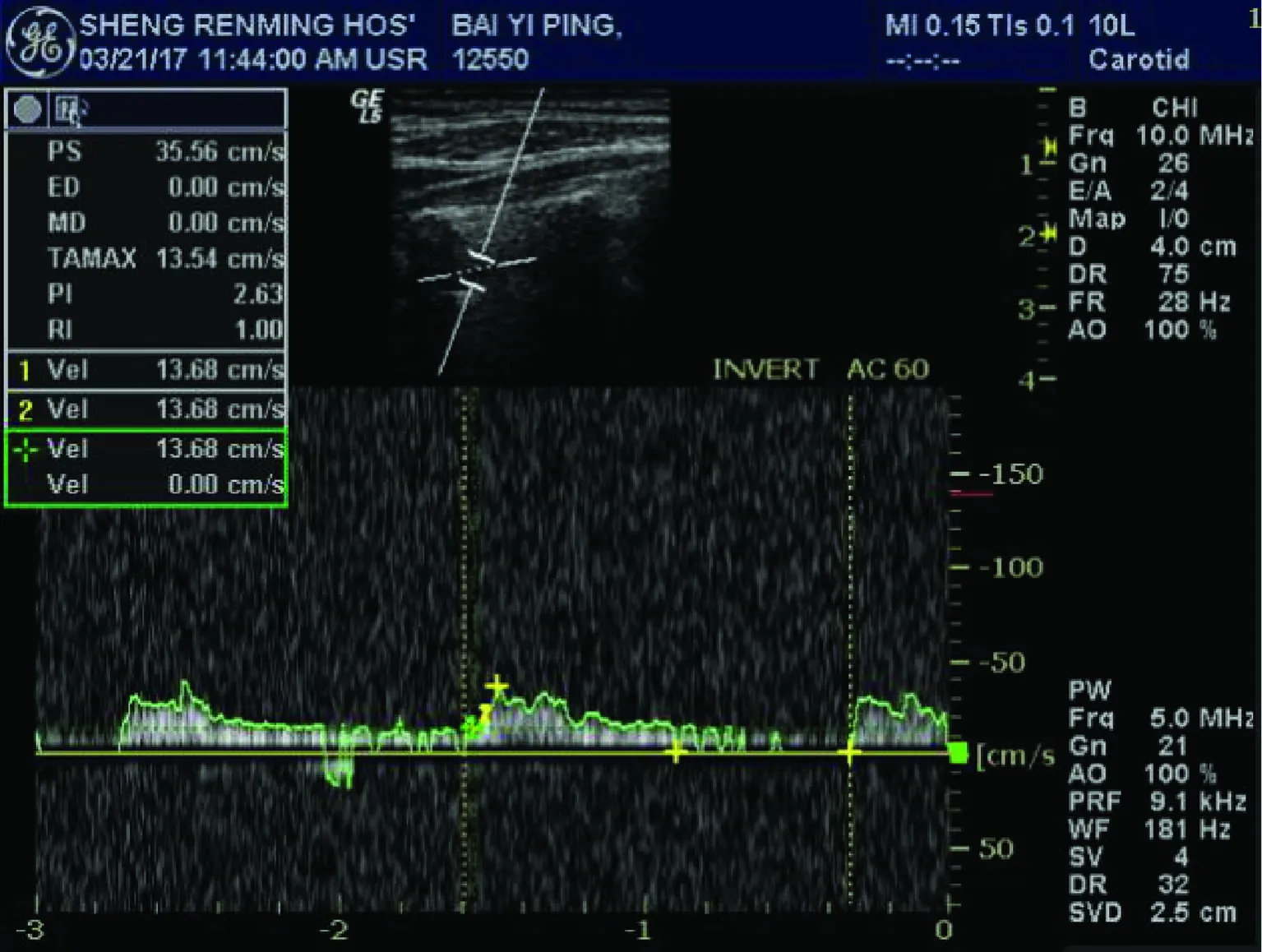
图4 正常人TCD信号
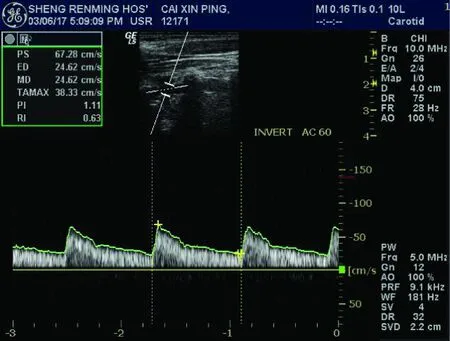
图5 斑块患者TCD信号
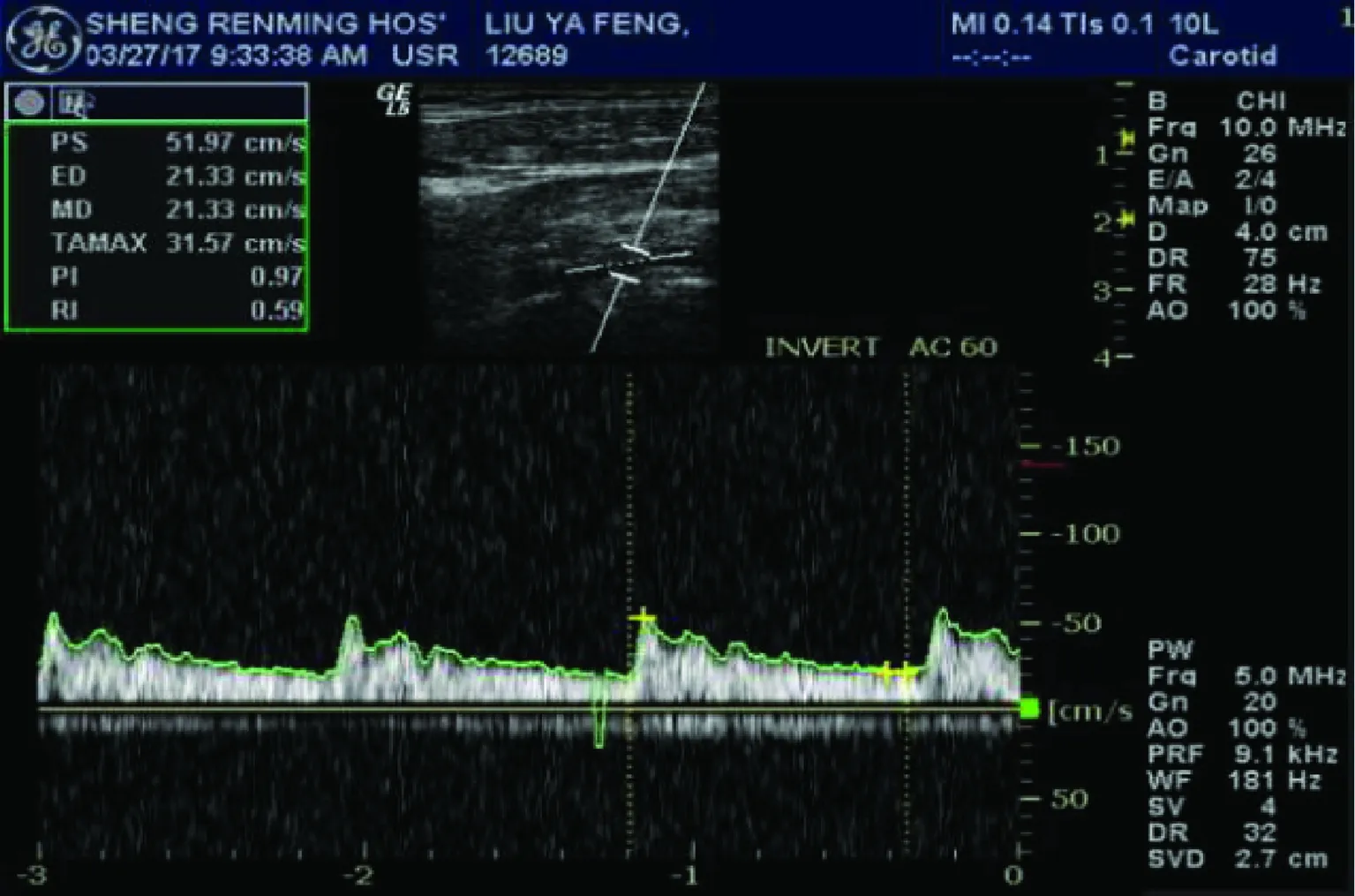
图6 狭窄患者TCD信号
通过与医学专家的磋商,在左侧颈内动脉、右侧颈内动脉、左侧椎动脉和右侧椎动脉4个部位采样以获得PSV(最大收缩速度)、EDV(舒张末期流速)、RI(阻力指数)、深浅程度和年龄情况等18个特征值,然后归一化提取特征值。将斑块和狭窄患者数据作为正类样本,正常数据被认为是负类样本。分别比较本文隶属度设计方法RFSVM、文献[7]中的OFSVM算法以及文献[8]中ZFSVM隶属度设计方法的Gm值。
根据文献[5]的结果,当C-/C+的值等于n+/n-时(n+、n-分别表示正负样本的个数),DEC算法效果最优,文中将正类惩罚因子C+设置为C,负类惩罚因子C-设置为C×n+/n-。
表1给出了对狭窄患者与正常人、斑块患者与正常人做分类的实验结果比较。
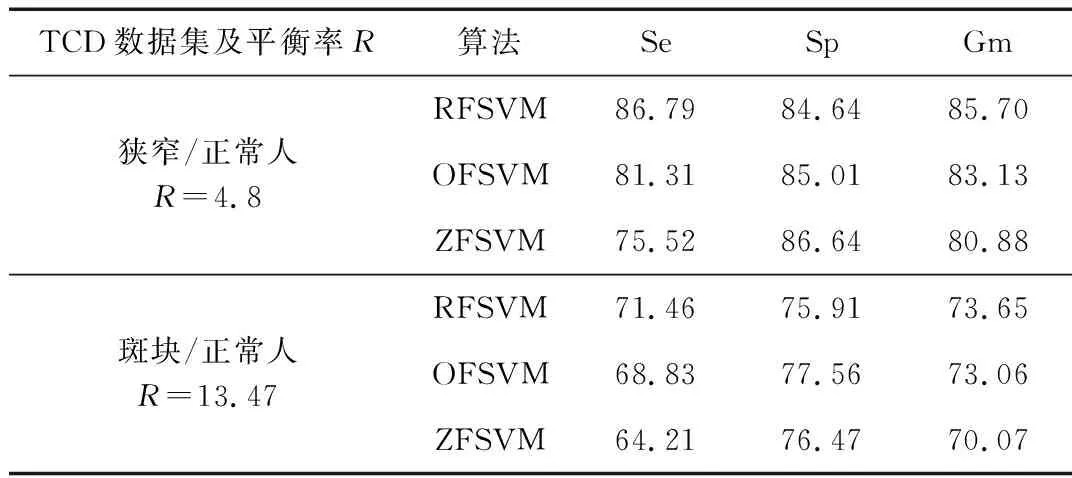
表1 三种算法的TCD数据集比较
为能更加直观地反映本文算法与另外两类算法的对比结果,将表1显示为图表形式,如图7和图8所示。

图7 狭窄与正常人分类比较结果

图8 斑块与正常人分类比较结果
从图7和图8中可以看出,本文提出的RFSVM算法在对TCD医疗数据做分类时具有较好的性能,特别是在改善正类(少类样本)识别结果方面。当不平衡程度比为4.8时,相比较ZFSVM算法和OFSVM算法,本文算法对少类样本的识别结果分别提升了11.27%和5.48%,整体性能Gm值提升了4.82%和2.57%。随着不平衡率的增加,当不平衡程度比为13.47时,相比较ZFSVM算法和OFSVM算法,其对少类样本的识别结果分别提升了7.25%和2.63%,整体性能Gm值分别提升了3.58%和0.5%。
4 结束语
为解决传统模糊支持向量机存在分类敏感和对支持向量赋予隶属度值不够精确等问题,本文提出了一种改进的模糊支持向量机算法,通过灵活设置半径控制因子优化训练样本范围,预选支持向量,将正类样本点到过平移后的负类中心超平面的距离和正负样本类中心距离值进行比较,将实线圆以内的样本点分为两部分,并对每一部分样本点精确赋值,同时剔除野值和噪声点,使得支持向量被赋予更大的权值,突出其对分类超平面的贡献。实验表明,本文提出的RFSVM算法在对TCD医疗数据的识别性能上有着显著的提高。但本文方法需要人工设置半径控制因子参数,设置参数时可能会把部分有效样本也剔除出去。下一步的工作是更加系统地研究参数与隶属度函数的关系,找到更为便捷的参数设置方法。

