基于流固耦合的密炼机动力学特性分析

张彦杰， 何延东， 朱向哲， 刘万锁

(辽宁石油化工大学机械工程学院，辽宁 抚顺 113001)

0 前言

密炼机是一种高效的混合机械，主要用于橡胶的混炼过程，物料在混炼室内，由转子自转带动物料运动，因此转子的工作性能直接影响混合效率[1]。近几年对密炼机流场的数值计算较多，如杨文超对剪切啮合型转子密炼机的混炼机理及实验进行了研究，汪传生对密炼机同步转子流场和异步转子流场进行了分析，边慧光对密炼机的三维流场进行了计算，但是都停留在稳态的计算[2-4]。本文使用Ansys软件，采用单向与双向瞬态流固耦合计算方法，对6WI型密炼机在3种不同工况下的内流场及结构场进行计算，从而进一步了解和掌握密炼机内部流动的客观规律，以便进行密炼机的优化设计。

1 计算方法

假设物料为不可压缩的非牛顿流体、流场壁面无滑移、流场为等温流场、忽略流体重力、流场内充满流体。采用Carreau数学模型描述流体性质[5-6]：

(1)

式中η(γ)——剪切率为γ时物料的黏度

η0——物料的初始黏度

λ——黏弹性特征时间

η∞——无穷剪切黏度

n——幂律指数

异步密炼机左右转子转速比为1∶1.15，为研究转速对转子应力变化的影响，分别对表1中的3种工况进行研究。

表1 工作状况Tab.1 Working condition

流场外层设置为稳态，流场内层设置为旋转域，动静交界面设置为Transient Rotor Stator，Interface关联为GGI。节点压力传递类型为Total Force，双向耦合计算时网格位移传递类型为Total Mesh Displacement。图1为计算的网格模型，网格类型为六面体网格，总数量为7×105。

(a)流体域 (b)固体域图1 网格模型Fig.1 Mesh models

2 数学模型

2.1 单向耦合

单向流固耦合计算中，采用顺序迭代耦合求解方法，这种弱耦合是将流场的瞬态数值计算结果直接由耦合面加载到结构场中，从而求得瞬态的固体应力结果[7]。结构静力学线性方程为[8]：

[K]{x}={F}

(2)

σ=[B][D]{x}

(3)

(4)

式中 [K]——刚度矩阵，N/m

{x}——位移矢量,m

{F}——力矢量，N

σ——应力矩阵

[B]——弹性矩阵

[D]——应变矩阵

σ1、σ2、σ3——一点上3个维度相互垂直的主应力，N

σe——米塞斯等效应力，N

2.2 双向耦合

双向流固耦合计算中，采用同步迭代耦合求解方法，这种耦合属于强耦合，其计算特点是流场与结构场同时计算，并及时交互计算数据。结构动力学线性方程为[9]：

(5)

式中 [M]——质量矩阵

[C]——阻尼矩阵

2.3 流固耦合界面

流固耦合界面是流场与结构场数据交换的重要媒介，耦合作用只发生在流体与固体接触面上，耦合关系由耦合面两边的协调条件引入，流体压力数据和固体位移数据由耦合面上的插值计算得到[10]。在流固耦合面上满足速度协调条件：

(6)

力平衡条件：

(7)

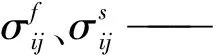
3 结果与分析

3.1 流场分析

1—双向耦合 2—单向耦合(a)剪切率波动时域图 (b) 剪切率波动频域图图2 流场剪切率曲线Fig.2 Shear rate curves of the flow field

为提高精度，流场计算时控制残差收敛精度小于10-5。流场模拟时长为20 s，步长为0.02 s，图2为密炼机在工况1下20 s内单向与双向耦合计算的流场剪切率曲线。单向与双向剪切率计算值相差1.539 %。从频域图可以发现，剪切率的变化主频为3.44 Hz,等于右转子的1倍棱倍频。第二主频为2.99 Hz，等于左转子的1倍棱倍频。单向与双向耦合计算在主频幅值上相差3.739 %。

3.2 应力与应变分析

图3为工况1下转子棱部的等效应力与变形量云图。可以发现，单双向耦合计算在转子应力及变形量分布上具有相似性。转子棱部的最大等效应力出现在棱部拖拽面的根部以及长短棱交接位置处，棱顶区具有最小应力。转子棱部位置由于啮合作用使得棱顶为大变形区域，背离转子啮合区的位置具有最小变形量，最大变形量出现在转速较高的右转子短棱边缘。

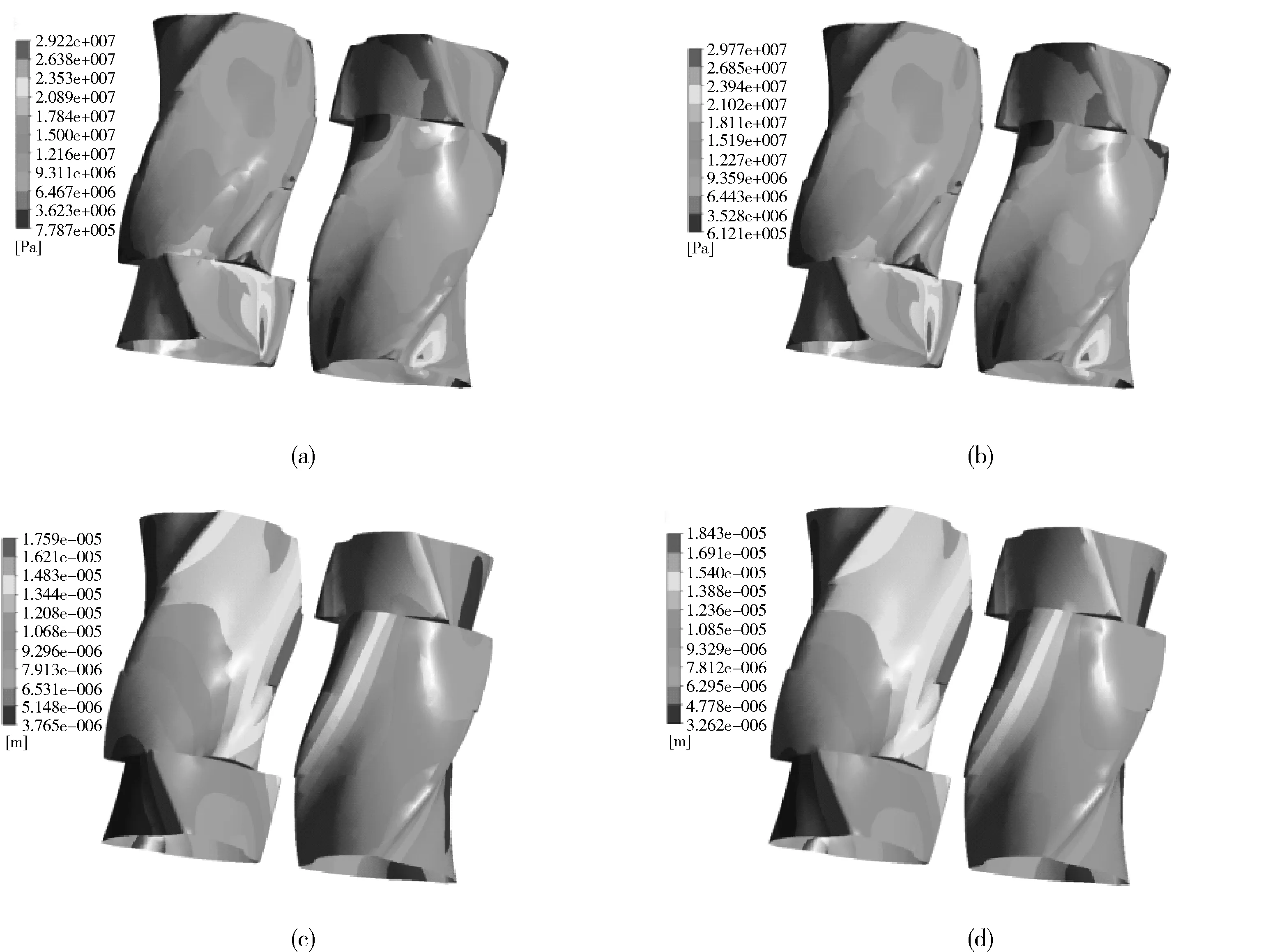
(a)棱部等效应力云图,单向耦合 (b)棱部等效应力云图,双向耦合 (c)棱部变形量云图,单向耦合 (d)棱部变形量云图,双向耦合图3 转子棱部等效应力及变形量云图Fig.3 Equivalent stress and deformation nephogram of the rotor edge

表2为3种工况下转子等效应力与变形量的计算结果。可以发现，最大位移处等效应力远小于最大应力处等效应力值，最大应力处等效应力差别较大，最大位移处等效应力差异较小。随着转速上升，单向与双向耦合计算结果在最大应力处和最大位移处的数值差异逐渐变小。

表2 单向与双向耦合计算的等效应力与变形量Tab.2 Equivalent stress and deformation under one-way and two-way coupling calculation

为进一步研究单双向耦合计算方法下，最大等效应力的振动规律，本文以工况1为例，对比了转子最大等效应力振动曲线。如图4(a)为转子最大应力位置和最大位移位置的应力变化曲线，可以发现，单双向耦合计算结果具有波动一致性，双向耦合结果高于单向耦合结果。在最大应力位置处，单双向耦合计算应力相差0.545 %。最大变形位置处，单双向耦合计算结果相差0.244 %。因此，在最大变形处不但具有较小的应力值，应力差也较小。图4(b)为转子最大应力位置和最大位移位置的应力变化频域图，可以发现，转子应力变化的主频集中在低频区，这是由于转子工作过程中，左右2个转子啮合作用造成的，而转子自转频率幅值很小，说明转子的振动受棱部影响较大，受自转频率影响较小。

1—双向耦合 2—单向耦合

图5为转子最大位移瞬态曲线。可以发现，转子最大变形量变化幅度较大，同时最低值差距较大但具有规律性。其变化曲线主频以转子棱部啮合频率为主，以1倍自转频率为辅。说明转子工作时的振动主要来自于转子棱部的啮合作用，而转子自转频率产生的振动较小。

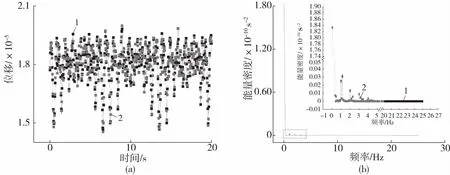
(a)时域图 (b)频域图图5 单双向耦合计算的最大位移瞬态曲线Fig.5 Curves of maximum displacement under one-way and two-way coupling calculation

(a)最大应力位置,工况1 (b)最大应力位置,工况3 (c)最大位移位置,工况1 (d)最大位移位置,工况3图6 工况1与工况3下转子最大应力曲线Fig.6 Curves of maximum stress under working condition 1 and working condition 3

同时从瞬态曲线图可知，每个时间步下，双向耦合计算结果都大于单向耦合计算结果，并且双向耦合计算可以更好地反应耦合面附近流体对于结构体的实时作用，能够更真实地反应结构振动状态，所以为保证分析结果的精确性，有必要考虑不同耦合计算方法的影响。由于单双向耦合计算结果具有一致性并且单向计算资源消耗较小，所以在粗略计算时，单向流固耦合计算可以替代双向耦合计算。

为进一步对比转速对于转子最大应力变化的影响，图6为转子分别在工况1和工况3下最大应力点与最大位移点的等效应力曲线。图6(a)中，在转子最大应力位置，工况3的高转速较小，转速波动幅值有一定上升，但整体波动平稳且相似，由频域图可知转速对于主频的影响较小，2种工况下的主频都集中在小于0.35 Hz的低频段，转子转频对整体波动影响不大。图6(b)中， 最大位移位置应力曲线随转速的变化情况与最大应力位置相似，同样能保持相同的波动和幅值，但从频域图可知，虽然小于0.35 Hz的啮合频依旧占据主导位置，但转子的1倍自转频与1倍棱倍频的影响变得显著，占据转子应力波动的次要位置。因此，转速上升对转子应力波动和频率有一定影响，但应力变化对于转速变化不敏感，影响转子应力波动与频率变化的主要因素是转子的外轮廓结构。

4 结论

(1)流场计算中，剪切率在单向与双向耦合计算结果相差1.539 %，主要工作频率为1倍棱倍频；

(2)单向与双向耦合计算结果在结构场中的差异较小，最大等效应力差为0.545 %，最大位移差为0.244 %，并且瞬态曲线波动具有相似性；随着转速上升，单双向耦合计算结果具有相同趋势；

(3)转子应力曲线波动对自转不敏感，受棱部几何结构影响显著，其应力主要频率为棱部啮合产生的小于0.35 Hz的低频段，应力波动在最大应力位置受转速影响较小，但在最大位移位置受转速影响较大。