微积分教学中的一题多解探讨
简慧 华东交通大学理学院 江西南昌 330013 沈冬梅 南昌工学院基础教育学院 江西南昌 330108
1 引言
微积分是高等数学教学的主体和核心内容, 是高等学校理工科和文管类大学本科生必须要掌握的重要基础, 因而学好微积分至关重要。 而极限理论是微积分学的理论基础,极限方法是微积分学的一种基本方法,极限思想和极限的运算贯穿整个微积分学的始终。在高等数学授课过程中,我们主要介绍了以下几种常见的求极限方法:(1) 多项式与有理分式函数(连续函数)代入法求极限;(2)消去零因子法; (3)无穷小因子分出法;(4)利用无穷小等价代换及运算性质; (5)利用左右极限求分段函数极限;(6)利用极限运算法则和两个重要极限;(7)利用单调有界准则和夹逼准则; (8)利用海涅定理(归结原则);(9)利用导数的定义;(10)利用洛必达法则; (11)利用函数的泰勒展开式等。本文结合日常的教学实践,只给出了函数求极限问题中比较典型的两类例子,利用上述求极限方法中的几种解法来分别求解同一类问题,并对各种解法的优缺点进行了简单分析,以此激发学生的学习兴趣, 启迪思维,帮助学生掌握求极限方法,在实际问题中做到活学活用,举一反三,由此提高高等数学课程教与学的效果, 提高教学质量和水平。
2.求极限问题中典型例题的一题多解

无穷小等价代换是求极限的一种重要方法,在商式求极限时可以大大简化计算。但特别需要注意的是,无穷小等价代换不猛滥用,一般只可对分式的分子或者分母中的因子(乘法或者除法运算)作等价无穷小代换,而分式的分子或分母中的函数的代数和中的无穷小不能分别代换再求极限。以下是学生中常见的一种错误解法:

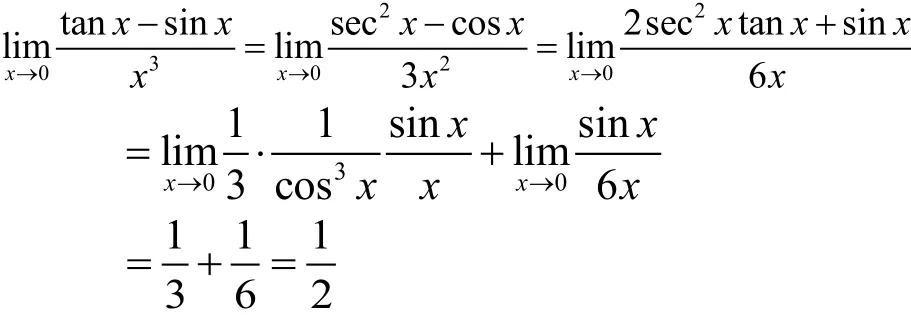
需要特别强调的是,在一次使用或多次连续使用洛必达法则求极限时,一定要验证商式是否满足洛必达法则的条件,足洛必达法则条件,此时洛必达法则不起作用,需要寻求其他方法(例如无穷小因子分出法)求极限。
解法4: 利用函数的泰勒展开式求极限

此种方法求极限对学生要求较高, 需要对相关函数的泰勒展开式非常熟悉,但对解题方法的积累和数学思维的训练大有益处。
再看下面的例子,该题在平时的教学过程中经常出现。
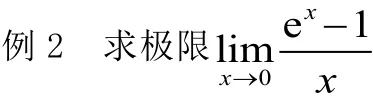
解法1: 变量代换后利用极限四则运算法则和重要极限
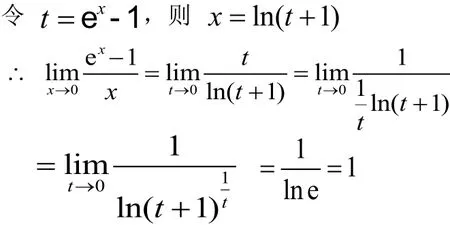
此种解法需要先进行变量代换,然后变成重要极限的形式,很多学生不容易想到,尤其是对刚接触两类重要极限的初学者。
解法2: 利用无穷小等价代换
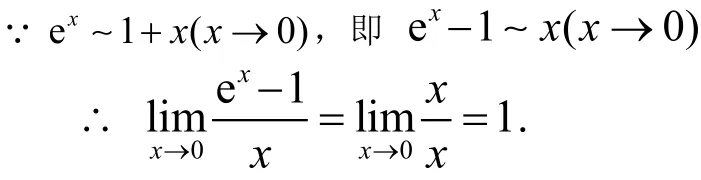
显然此题利用无穷小等价代换求极限非常简单。


此题中分式函数的形式比较简单,大部分学生会利用此方法求极限。
解法5: 利用函数的泰勒展开式求极限
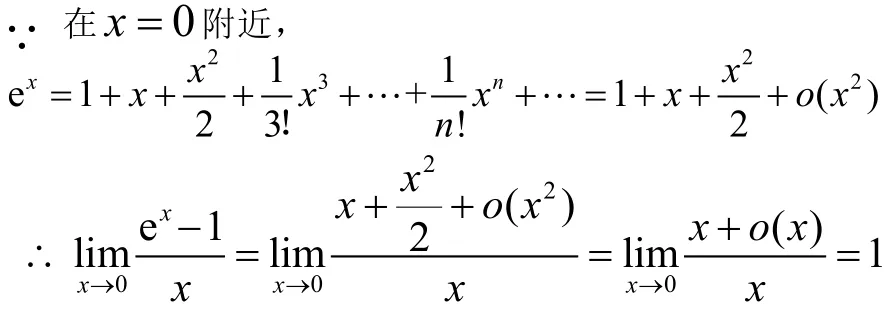
与前面四种解法相比,该解法相对复杂些,学生很少用此法解题,但作为解题方法的积累,平时也要加强训练。
结束语
本文通过对两类求极限问题一题多解方法的探讨,而并没有列举出更多的例子,旨在通过典型例题说明求极限的方法变化多样,需要认真分析问题中函数极限的具体类型,灵活地运用上述求极限方法中的一种或几种方法结合来求解,通过比较得到最便捷的计算方法。 以此来激发学生学习大学数学课程的兴趣, 启迪思维,培养学生的创新能力,提高高等数学课程教师教与学生学的效果, 提高教学质量和水平。

