产业协同集聚对制造业效率的影响研究

刘玉浩 池仁勇 施佐利

（1.浙江工业大学 经贸管理学院，浙江 杭州 310023；2.浙江工业大学 中国中小企业研究院，浙江 杭州 310023）

0 引言

随着全球经济不断迅猛发展，制造业和服务业在空间上的互动发展形成了你中有我，我中有你的格局，其主要原因在于二者自身特点的变化，使得两者之间的界限越来越模糊。制造业企业除了单纯地生产和加工商品以外，同样也看重消费者的消费感受，为消费者提供产品的售中和售后服务。而服务业企业也不单单只提供服务，它凭借其丰富的顾客源和多样化的渠道，逐渐向制造业企业延伸，不断完善其产业链。这种产业间相辅相成、相互促进的协同集聚方式，不但在我国形成了新型的产业发展模式，也为制造业效率的提升提供了新的解决思路和方法。

现有研究表示，由于产业间的相关性，生产性服务业和制造业的协同集聚，可利用的要素资源更为丰富，可以达到促进制造业转型升级、同时提高其效率的目的。但是，过度集聚又会造成基础设施拥挤、争抢要素资源、环境污染等负面效应，进而导致制造业效率的下降。所以，协同集聚和制造业效率之间可能是更加复杂的非线性关系。对于我国这样一个制造业大国，现在处在新旧动能转换、转型升级的关键时期，探究生产性服务业和制造业协同集聚会对制造业效率产生何种影响具有重要的现实意义。

本文在结合相关理论以及文献研读的基础上，运用静态面板数据回归模型和GMM回归模型，探究生产性服务业和制造业协同集聚程度。如何影响制造业效率，并提出实际的应用价值，为我国制造业效率的提高提供一定的参考作用。

1 生产性服务业与制造业协同集聚对制造业效率的影响机理

1.1 促进效应

产业集聚可以在空间地理上获得要素资源共享和信息技术溢出等优势。

一方面，由于生产性服务业和制造业之间有着明显的供需关系，所以当制造业周围集聚了大量生产性服务业时，就可以利用生产性服务业的产出成果作为中间产品投入制造业中，使制造业获得更多先进技术，在此基础上改进现有的生产方式，缓解可能存在的生产不经济现象。这种空间地理上的邻近，不仅减少了生产性服务业和制造业之间因为业务往来所产生的交易成本，还可以降低信息获取和接收的成本，为制造业效率的提高奠定基础。

另一方面，产业集聚的地区往往也是知识和技术较为密集的地区，不同企业之间的交流合作会促进知识和技术的外溢，产业间知识外溢的基本表现形式为一种互补型的知识外溢。对于生产性服务业和制造业而言，主要表现为研发合作的知识外溢机制。在协同集聚区域内，不同产业的信息、知识、技术互相交流和碰撞，促进企业的自我完善和发展，从而促进制造业效率的提升。

1.2 抑制效应

抑制效应主要表现为生产要素的拥挤效应，其会导致制造业效率的下降。具体而言就是投入要素的过度增加导致投入产出比失衡，进而影响到产业效率。某地区发生产业过度集聚现象的原因包括两方面的内容，一是产品恶性竞争，二是基础设施拥挤。

1.2.1 恶性竞争

由于地区资源的承载能力是有限的，当某一地区内集聚的企业过多时，企业之间为了争夺有限的资源和市场，就会发生恶性竞争现象，造成土地、劳动力等要素资源价格的上涨。此外，我国产业发展程度依然较低，产品同质化严重，易于被抄袭和模仿，更加剧了竞争的激烈程度，最终导致企业生产效率的下降。

1.2.2 基础设施拥挤

发达的基础设施有利于企业降低运输和通信成本，促进产业在某地区的集聚。但是，地区的承载能力是有限的，当产业集聚程度大于基础设施的承载力时，其对该地区经济的影响就会由正转负，在当前情况下，企业会选择离开中心集聚地区，搬到更加适合其发展的区域。

由上述分析可知，本文认为协同集聚对制造业效率的影响会随着协同集聚程度的不同而不同，总体来讲是促进效应和抑制效应的综合，即生产性服务业和制造业的协同集聚指数与制造业效率的影响呈现倒U型的关系。首先，当协同集聚指数较低时，产业集聚通常是在类似的企业或部门分布的，形成区域经济，这些同类型的企业相互竞争、学习以及共享资源。这时生产过程逐渐增多，为了节约运输成本和靠近消费市场，越来越多与产业密切相关的企业进入市场，形成协同集聚的模式。协同集聚通过不同产业间的良性互动与融合，逐渐形成产业技术创新、知识外溢等外部效应，推动产业的优化升级，提高生产效率。但是，当协同集聚程度进一步加深时，受到资源、环境等条件的限制，协同集聚不断提高所带来的拥挤负效应日益凸显，并逐渐超过规模扩大所带来的收益，进而对制造业效率的增长产生抑制作用。

2 模型设定与变量描述

2.1 模型设定

基于上述分析，为了更精确地度量生产性服务业和制造业协同集聚对制造业效率产生的影响，本文采用面板数据回归模型进行实证分析。模型如下：

其中：下标j，t分别表示地区和时间；ME表示制造业效率；C表示生产性服务业和制造业的协同集聚指数，由于二者的协同集聚指数和制造业效率之间可能存在非线性关系，因此在模型中加入协同集聚指数的二次项；C0n表示控制变量；α0是常数项；ε表示随机误差项。

2.2 变量说明和数据来源

2.2.1 变量说明

（1）制造业效率（ME）

制造业效率是本文的被解释变量，在一些研究中，通常选取劳动生产率、制造业产出率等作为度量指标。本文选取劳动生产率作为衡量制造业效率的指标，即制造业总产值与其全部从业人员数的比值。其中，制造业总产值和全部从业人员数均由统计年鉴中制造业细分行业加总得到。

（2）生产性服务业和制造业协同集聚指数（C）

生产性服务业和制造业的协同集聚指数是本文的解释变量。测量产业集聚的方法很多，包括基尼系数、胡弗系数、区位商、赫芬达尔指数、E-G指数等。考虑到数据的可得性，本文借鉴陈晓峰的做法，利用生产性服务业和制造业的区位熵构建二者的协同集聚指数。具体公式如下：

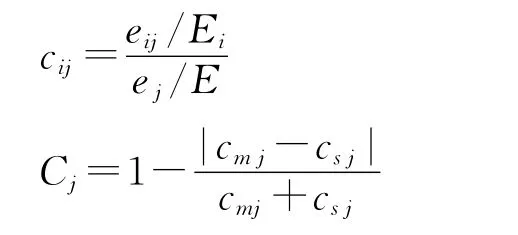
其中，cij表示j城市i行业的区位熵，eij代表j城市i行业的产值，Ei表示全国i行业的总产值，ej表示j城市所有行业的产值，E表示全国总产值。Cj的含义为j地区生产性服务业和制造业协同集聚指数，cmj的含义为j城市制造业的区位熵，csj代表j城市生产性服务业的区位熵。j城市制造业和生产性服务业的集聚程度越接近，Cj值越大，表明协同集聚程度越高。

（3）主要控制变量

（a）经济发展水平（Eco）

经济发展水平主要通过影响生产力的发展，进一步影响制造业的效率，它主要体现了各个产业的综合发展情况。孔婷等通过实证研究表明经济发展水平会对制造业效率产生积极的促进作用。现在许多研究都采取人均GDP作为指标度量国家的经济发展水平，本文借鉴这种做法，选用人均GDP来度量我国的经济发展水平。

（b）人力资本水平（Edu）

随着社会的进步，单纯地投入体力劳动已经无法满足现代制造业的需要，人力资本正取代劳动力成为制造业主要的投入方式。范剑勇等人认为人力资本存量会对制造业效率产生影响。本文选取大专以上学历人口数占6岁以上人口数的比例代表该地区的人力资本存量。

（c）技术创新能力（Techin）

先进的技术创新能力不但可以减少劳动力成本，还可以提高制造业的技术水平，推动产业发展，使制造业获得竞争优势，从而提升制造业的产出效率。为了合理度量技术创新能力，本文借鉴孔婷的做法，选取各省历年的专利申请数作为衡量指标。

相关变量的描述性统计如表1所示。

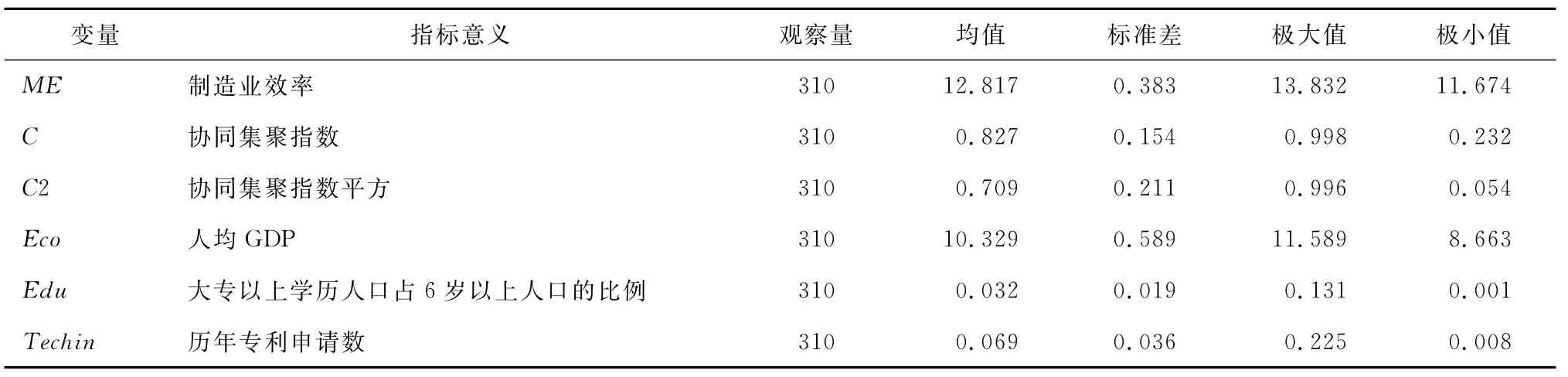
表1 变量描述性统计

2.2.2 数据来源

本文选取2006—2015年全国31个省份的数据进行分析，主要数据来源于2007—2016年《中国统计年鉴》以及各省统计年鉴，缺省数据用插值法补充。

3 面板数据模型回归结果分析

3.1 静态面板模型分析

面板数据回归方程的估计模型主要有固定效应模型（FE）、随机效应模型（RE）、混合效应模型（Pooled OLS）。我们利用LR检验和hausman检验，结果显示模型应该采用个体时间双固定效应模型。采用Stata对模型进行回归分析，具体结果见表2。

从表2中可以看出，生产性服务业和制造业的协同集聚指数前面的系数为正，协同集聚指数平方前面的系数为负，而且都在1%的显著性水平下统计显著，这一结果证明了生产性服务业和制造业协同集聚与制造业效率之间存在倒U型关系。也就是说，生产性服务业和制造业协同集聚对制造业效率是先促进、后抑制的效应。因此，产业协同集聚在经济发展过程中，在不同阶段表现是不同的，分别表现为促进效应和抑制效应。在产业协同集聚萌芽时期，生产性服务业和制造业会相互寻找合作企业，这使得企业之间形成了复杂的网状联系，进而形成了互相连接的有效网络。在产业关联的效应下，人才、资源、资本有效地流动融合和发展，产业直接的协同效应会带动制造业和服务业本身的收益递增，促进制造业效率的提高，实现产业结构升级。然而，当产业协同集聚发展到一定阶段时，会出现集聚不合理的现象，当前城市的公共基础设施和当地市场会超出它原本的承载力，直接表现为城市人口膨胀、交通堵塞、产品生产成本上升、企业利润下降等不利于制造业劳动生产率提高的现象，在某种程度上导致了制造业效率的降低，协同集聚带来的优势效应不能得到发挥。

表2 静态面板模型回归结果

我们从表2中还可以看出，经济发展水平在1%的显著性水平下通过检验，说明经济发展水平可以正面促进制造业效率的提升。这一方面说明随着经济发展水平的提高，顾客不再只追求价格便宜的产品，对制造业产品质量也有更高的要求，这在某种程度上间接促进了制造业效率的提升；另一方面，制造业仍然保持着国民经济支柱的地位，较高的制造业效率对应着较高的经济发展水平。

人力资本水平对制造业效率有促进作用。原因在于，制造业就业人员拥有越高的思想道德素质、专业素养，解决问题的能力也就越高，同时这也大大增加了科研人员参与制造业活动的比例，使制造业逐渐由劳动密集型向技术密集型的方向发展，达到提高制造业效率的目的。

技术创新能力虽然会对制造业效率产生一定的影响，但并未通过显著性检验。这说明技术创新能力能否提高制造业效率仍有待商榷。主要原因可能是我国现在仍然以劳动密集型产业为主，技术密集型产业的数量虽然逐年增多，但是仍然只占少部分，技术创新的需求依然不足。

3.2 GMM模型结果及分析

考虑到面板数据可能产生的内生性问题，本文采用GMM模型进一步分析，消除内生性问题。在工具变量选取方面，采用制造业效率的滞后项作为工具变量。GMM模型回归结果如表3所示。

从回归结果看，生产性服务业和制造业协同集聚一次项系数为正，二次项系数为负，验证了静态面板数据先促进、后抑制的结论，协同集聚对于制造业效率的影响呈现倒U型的形态，与静态面板数据回归结果一致。

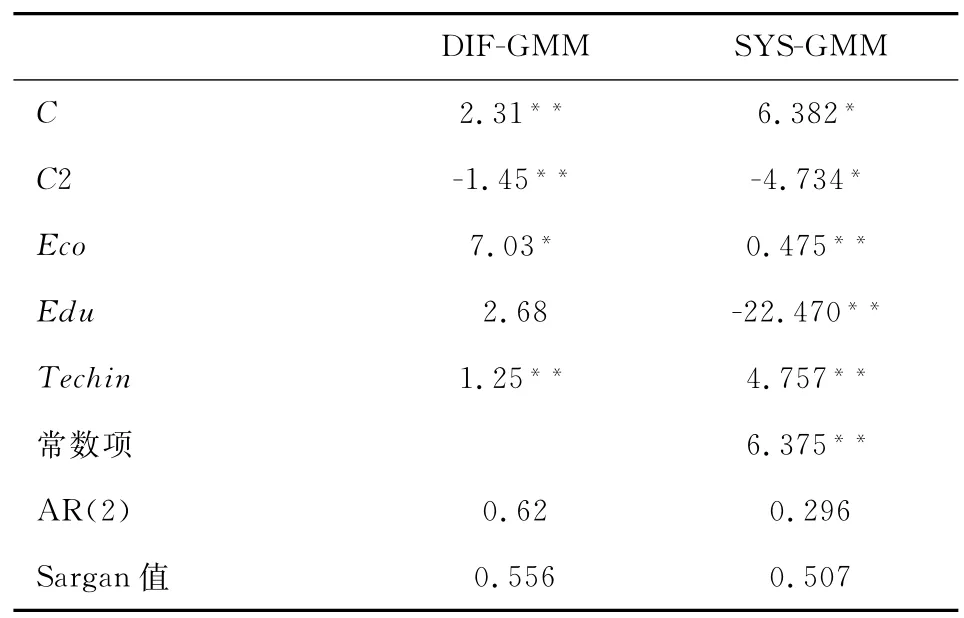
表3 GMM模型回归结果

4 结论

本文运用面板数据计量模型，探究了生产性服务业和制造业协同集聚对制造业效率的影响，发现二者倒U型关系明显。这说明，适当程度的集聚对制造业效率有一定程度的促进作用，但是过度集聚所引起的资源拥挤、恶性竞争等对制造业效率又存在抑制效应。也就是说，在保持其他条件不变的情况下，产业协同集聚指数有一个最优值，政府可以通过该数值判断当地是否存在产业过度集聚现象。当某地区协同集聚程度远远低于最优值时，应当采取相应的政策鼓励二者共同发展，提高制造业效率。相反，应该适当外迁部分企业，使协同集聚程度保持在合理范围内。

本文提出如下政策建议：

（1）生产性服务业要和制造业协调发展，互相适应。在制造业的发展过程中，不应该过分看重经济服务化，还应该根据各个城市制造业的自身特点、发展阶段的不同，用更加科学理性的方法调整二者之间的关系，在提高制造业效率的基础上，扩展其产业价值链，帮助其升级产业结构和提高产品竞争力。

（2）建立产业协同机制。对于协同集聚程度较低的城市和地区，制造业应适当进行服务外包，培育与其相关的服务行业，保持要素资源在地区内合理流动，形成产业合力。鼓励优势企业提供更完善的生产性服务，同时利用其新颖的商业模式，把企业的文化、技术、市场信息与周围企业分享，带动他们协调发展。

（3）不同地区的产业协同集聚程度不同，所能带来的影响也不同。对于发达程度较高、技术较为先进的城市，应注重二者的协同发展，利用其资源优势实现生产效率的提高；对于经济较为不发达的地区，应该首先注重制造业企业的发展，利用其产生的知识外溢效应，提高生产效率，达到实现经济增长和社会发展的目的。