考虑道路拥堵程度的出行路径规划研究

杨晓颖 纪道元

（1 北京交通大学,北京 100044；2 雅各布大学，不来梅 28719）

引言

随着社会的发展，汽车给人类的出行带来了非常大的便捷，但是由于车辆数量的快速增加使得城市中交通拥堵成了常态。人们常因不熟悉道路交通状况、交通拥挤和道路堵塞，导致时间延误、疲劳驾驶甚至是交通事故的发生，这无疑产生了极大的交通安全隐患，甚至影响了社会经济的发展和人们的日常生活。

几十年来国内外的科学家提出了多种路径规划的求解方法，比如Floyd算法、Dijkstra算法等。其中，Floyd算法易于理解且设计方便，在城市最短路径规划中使用非常普遍。国内外学者对Floyd算法进行了深入的研究[1-5]。徐达、蔡满春等人通过去除中间非必要节点路径对Floyd算法进行了改进，有效提高了Floyd算法的计算效率；左秀峰、沈万杰研究了基于Floyd算法的无相连通图中多重等价最短路径算法；张德全等提出了Floyd加速算法及优化方法。

通过分析发现，随着城市道路交通网络各种基础设施的不断完善以及现代科技的不断进步与发展，最优路径规划算法也从传统的静态最优路径规划向着动态最优路径规划方向发展。但目前的路径引导系统多是从道路利用者的角度出发，即使道路利用者的自身出行成本最小，而忽略了道路网络的系统平衡。

若从全局角度出发，即从决策者的角度出发，先对道路网的运行信息加以分析处理，得到已陷入或即将陷入拥堵的路段信息，在进行路径规划时回避掉这些路段，既能提高道路利用率又能在一定程度上缓解道路网上的交通压力，加速拥堵路段的疏通。

基于上述考虑，本文将Floyd算法与道路拥挤程度相结合，得到一种改进的最优路径算法。经过算法的编程实现，得到一条规避掉拥挤路段的最优路径，比较符合实际。

1 路段交通状况判断

在路径规划中考虑道路拥挤问题，必须将道路拥挤这一因素进行量化。车辆行驶过程中，路段上的行车速度是与行车效率最密切相关的一个指标。若路段上行车速度相对平时快，则通过该路段的时间相对少。

根据我国公安部2002年公布的相关标准，目前我国相关交通管理部门对城市道路交通状态的量化定义主要运用主干道上的机动车平均速度大小来描述其拥挤程度[6]，具体定义如下：

（1）畅通：城市主干道上机动车的平均速度不低于30km/h。

（2）轻度拥挤：城市主干道上机动车的平均速度低于30km/h，但高于20km/h。

（3）拥挤：城市主干道上机动车的平均速度低于20km/h，但高于10km/h。

（4）严重拥挤：城市主干道上机动车的平均速度低于10km/h。

公安部关于交通拥挤的定量描述具有较高的可操作性，可直接用于道路交通状态的判别。

由于本文在进行路径规划时只考虑路段是否已经陷入拥挤或即将陷入拥挤，故而将上述交通状态的量化定义重新定义为：

（1）不拥挤：城市主干道上机动车的平均速度不低于15km/h。

（2）拥挤：城市主干道上机动车的平均速度低于15km/h。

本文所需的速度需从车联网系统中直接获得，且根据路段距离和速度获得仿真中所需的时间。

2 最优路径规划的算法设计

2.1 道路网络的抽象化及其数学模型描述

路网通常被抽象为图论中的“图”，可构建一个路网模型[7]如下:

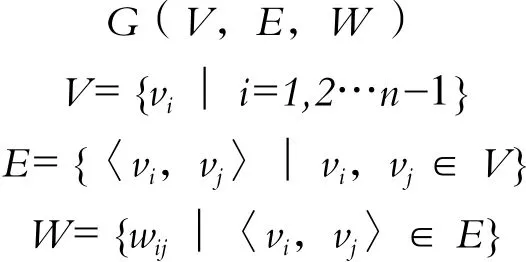
其中，V表示节点集；E表示边集，且〈vi，vj〉和〈vj，vi〉属于不同的边；W表示权重集，可选择不同的标准作为权重，例如时间、距离等；wij表示节点i和节点j之间的权重。对于实际的道路网络，一般情况下同一路段两个方向的交通信息是不相同的，因此使用有向图来表达实际路网，单行道中不可行车方向的距离（行驶时间）可设置为最大值。

道路权重也称道路交通阻抗或路阻，它的确定与计算是最优路径规划算法优化目标的依据。路阻一般选择距离或时间，由于出行者出行时大多希望在最短时间内到达目的地，故本文采用时间作为路径规划的依据且在设置各路段路阻值时，若某一路段为拥挤路段，则该路段路阻值记为最大值，如1000。

2.2 Floyd算法的思想及过程

①Floyd算法的思路是：

设vi，vj是网络G（V，E，W ）中点的集合V中的任意两点。令为vi到vj不经过中间点的最短路路长，显然。

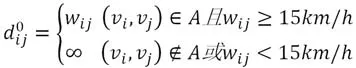
②改进后的Floyd算法的步骤如下：

第一步：k = 0

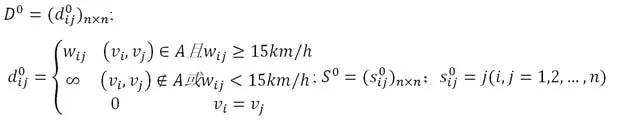
第二步：k = k+1

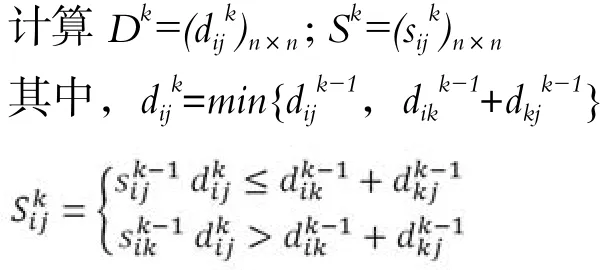
第三步：当k=n时算法结束

Dn=()n×n,n是vi到vj的最短路路长; Sn=(S)n×n,是vi到vj的最短路的第一条弧的终点。

2.3 实例分析

① 以山东省青岛市黄岛区一实际路网为例，抽象成路网图，如附图所示。图中所有路段均为双向路段；图中各节点均为十字路口，图中所标距离均为路口与路口之间的路段长度，如路口1和路口2之间的路段长度为1190m。

文中要搜索节点1到节点12的最短路径。

② 文中所采用的初始数据见表1。

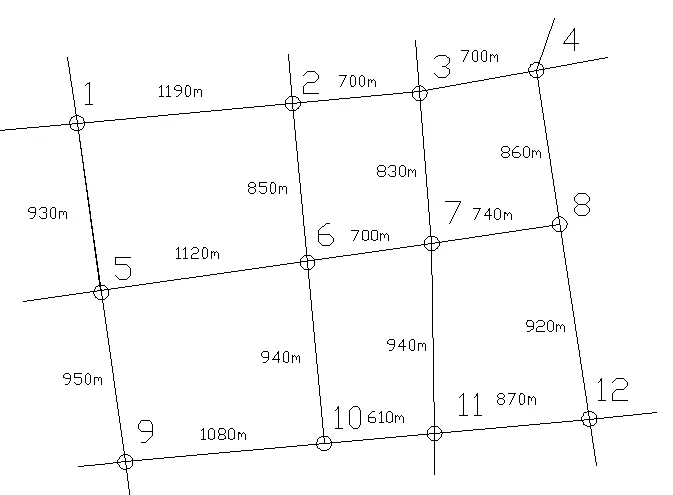
附图 路网抽象图

表1 初始数据

上述数据观察得知节点2与节点3之间、节点2与节点6之间、节点7与节点8之间以及节点10与节点11之间的路段运行速度均小于15km/h，由1给出的路段拥挤程度判断标准得知上述四条路段为拥挤路段。

文中所采用转换后最终数据见表2（考虑到程序的运行，拥挤路段时间记为1000s）。

表2 最终数据

③ 根据2.2所述算法，编制出Floyd算法程序代码，在Codeblocks平台上运行该程序代码得到节点1到节点12的不含拥挤路段的最优路径为1 →5→6→7→11→12。若不考虑所得路径是否含有拥挤路段，则得到节点1到节点12的最优路径为1→5→6→10→11→12（其中10→11为拥挤路段）。

两条路径相比，第二条路径经过了拥堵路段10→11，对整个道路网而言加剧了道路拥堵状况；而第一条路径虽对出行者个人来说并非是出行成本最小的路径，但从整个道路网络来说，可以使得道路网络趋于平衡并将拥挤路段的道路交通压力分散到临近非拥挤路段上去，从而提高了道路利用率。

3 结束语

从决策者角度出发的最优路径规划考虑了整个道路网的平衡，在考虑拥挤路段的影响后，使用Floyd算法，使得求出的最优路径更加符合实际情况，且能有效地避免出行者陷入交通拥挤，在一定程度上解决交通拥堵问题。在路径规划中还可以将交叉口红绿灯的延误、所含交叉口个数、弯道长度等因素考虑进去，以使求得的最优路径更加符合实际情况。