基于多目标遗传算法的低碳公交网络优化
谭 倩,常柱刚
(长沙市规划设计院有限责任公司,湖南 长沙 410007)
随着我国私人小汽车数量的迅速增长,城市交通拥堵与环境污染问题越来越严重.公共交通是缓解城市交通拥堵的有效途径,但由于我国公交服务差,导致公交出行分担率低,公共交通缓解城市交通压力的作用没有得到充分发挥.要提高城市公共交通出行分担率,合理的公共交通网络至关重要.公交网络设计合理,可以减少出行者换乘次数,提高出行的便捷性,也会极大提高民众公交出行的意愿.此外,尽管很多城市采用电动公交,由于电动公交续行能力有限,而且充电慢,目前还难以全面普及.混合动力的公交车更为实用.如何设计有效的公交网络,同时尽可能减少公交碳排放量,是学者需要研究的课题.
国内众多学者对公交网络的设计从各个方面开展了研究.刘好德[1]以居民出行时间和无有效公交出行路径出行量两者出行成本最小为目标,提出了一种基于路线优选的优化模型,并引入模拟退火拉伸遗传算法求解;满英等[2]以居民出行时间和投资最少为目标函数,并用模拟退火-遗传算法组合算法进行求解;赵德川等[3]以居民出行时间最短为目标函数,并提出了线路长度、非直线系数、乘客换乘系数、线路满载率等约束条件,并用免疫遗传算法求解;其他学者针对公交站距优化、网络设计中考虑公交调度等方面开展研究[4-14].国外学者Lee和Vuchic先寻找出最短路,形成备选路段,再通过迭代淘汰效率低下的线路,达到优化线路目的[15];Mariano Gallo等[16]考虑居民出行弹性需求这一因素,将出行外部成本内部化.Ceder等提出一种使公交系统时刻表同步的模型,它以发车间隔作为每条线路的变量,使不同线路的公交车同时到达换乘站点,模型较为复杂,适用于在小型网络中求解[17];Cevallos以线路现状发车间隔和发车时间作为输入,应用遗传算法协同公交系统的时刻表,整个过程虽未建立数学模型,但通过算法使乘客换乘等待时间最短[18];Shafahi和Fujita M,Dell等学者以公交网络总的换乘时间最短为目标,建立了数学规划模型达到优化公交网络的目的[19-21].
本文引入低碳这一目标函数,兼顾居民出行和企业运营成本,综合这三方面目标,优化公交路网.并建立双层规划模型,用遗传算法进行求解.
1 问题描述与符号定义
1.1 问题描述
公交线路(公交线)一般是指在公交网络中两个节点间运行的一组车辆的线路,这些车辆的大小、运载能力及运营特征相同,并且每次运行所经过的节点和路段也相同.在已知城市公交客流OD以及城市路网结构情形下,考虑如何构建城市公交线路的走向,包括起点(首站)、终点(末站)以及公交线路的路径,以实现采用尽可能少的公交车辆、乘客出行时间尽可能减少等目标.
1.2 符号定义
符号定义如下:
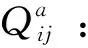
2 模型构建
2.1目标函数
城市公交线网的优化问题是个复杂的非线性问题,涉及因素很多,其问题的关键是目标函数的选取.在不同情况下,不同学者对公交线网优化的目标函数选取不同.本文从乘客利益、公交企业利益、公交可持续发展三个方面考虑,提出三个关键的公交线网优化目标函数.
(1)乘客总出行时间
在进行公交线网优化的过程中应首先考虑乘客利益,合理线网应尽量节约乘客出行时间,保证较低的换乘率,提高乘客公交出行的直达率.因此,乘客总出行时间最短是公交线网规划社会整体效益最显著的目标.
(1)
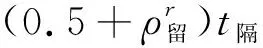
(2)公交运营成本
公交线网优化过程中,必须适当考虑公交企业的运营成本,使其能以低成本运营而获得较好的收益,提高企业的运营活力.
(2)
(3)公共交通污染物排放量
公共交通污染物排放量反映了公交系统的环境负效应,在满足一定的公共交通需求的前提下,污染物排放量越少,公交效率越高.
(3)
式中,h=1,2,3,4分别表示CO、CO2、NOx和CHx.
最后将三个目标函数进行加权,得到最终的目标函数:
(4)
式中,α、γ、θ为权重系数.
2.2 约束条件
考虑到城市公交的服务属性要求,兼顾其效率与优先两个方面的约束条件,城市城际公交网络设计优化目标的约束条件如下:
2.2.1 公交线长度约束
公交线不宜过长也不宜过短,线路太长,会影响车辆的运行时间,增加驾驶员疲劳度,会影响到乘客等车时间.线路太短,则会增加乘客的换乘次数,相对增加了起终点的停靠时间,影响企业效益.另外,纯电动公交车还具有更加严格的长度限制.公交线长度约束为:
LminLmax
(5)
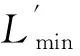
(6)
2.2.2 线路非直线系数的限制
如果线路拐弯过多,行驶不便,也易引起道路阻塞和交通事故频发,但由于城市地理形势实际限制,所有线路不可能都是直线.所以通过综合分析,线路非直线系数不宜大于1.4.
非直线系数为:
(7)
2.2.3 直达率的限制
不能直达则会增加乘客途中时间和精力的消耗,使之感到不便,但由于经济发展的限制,不可能让每个乘客都直接到达目的地,所以一般需要要求直达率不能低于γmin.
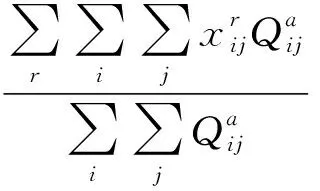
(8)
2.2.4 线路负载效率系数的限制
一条线路不同部分的负载要均匀,才能提高线路运能的利用率,降低营运成本,一般情况下要求线路负载效率系数达到60%以上.
线路负载效率系数为:
(9)
式中,n为路段的总数.
2.3 双层规划模型
通过以上分析,建立了基于多目标的城市公交网络设计双层模型,上层为一个NDP问题,下层为一个基于随机用户平衡的公交客流分配问题.模型表示如下:
(10)
St:
LminLmax
(11)
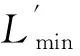
(12)
(13)
ρ1.4
(14)
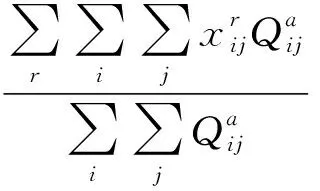
(15)
(16)
ηminηηmax
(17)
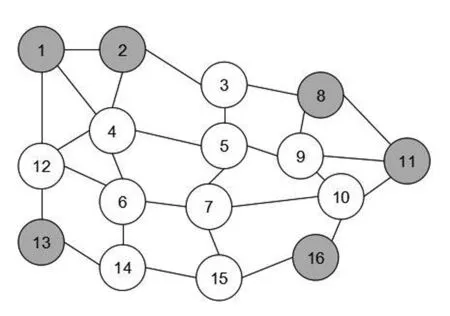
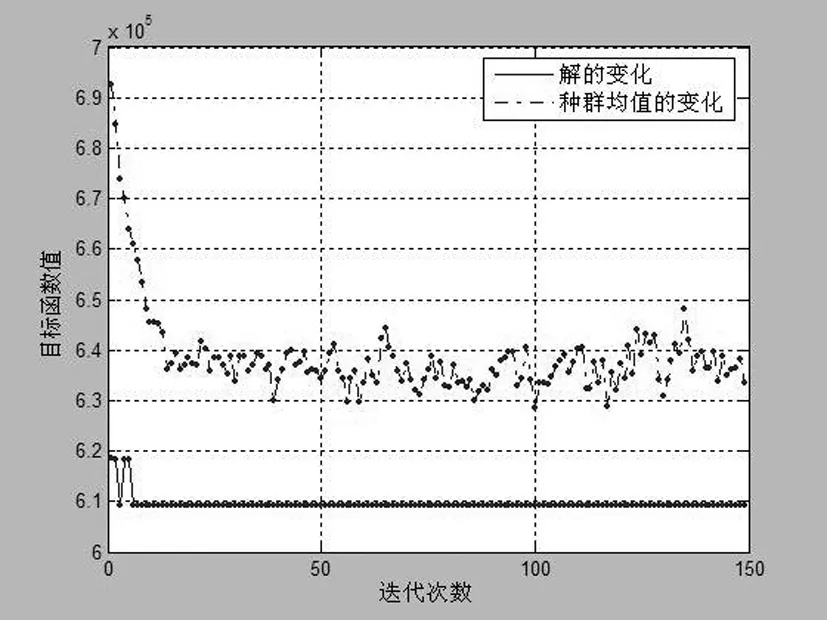
g (18) [TAP]: (19) St: (20) (21) (22) 双层规划模型是NP完全问题,路网复杂时,难以得到最优解,一般可通过智能算法求近优解.因此,本论文采用遗传算法求解以上双层规划模型. 本文的遗传算法编码部分采用二进制方式编码.这个模型中,先确定每条公交线路的首末站点,结合约束条件,生成多条较短路径并编号,即各个候选路线的编号;将编号转化为二进制,再根据线网规模大小决定编码长度. Step1:随机产生N个初始解,即初始种群,这一过程相当于在所有可行路线当中随机选择编号组合作为初始解; Step2:设置最大进化代数,输入交叉变异等概率参数,以及OD数据、节点距离等网络数据; Step3:转到下层求解基于路径随机用户平衡的公交客流分配; Step4:根据下层的客流分配结果,转到上层求解目标函数; Step5:计算各个染色体的适应度,并进行选择; Step6:根据交叉变异参数进行染色体交叉和变异操作,并判断是否达到结束进化条件,未达到结束条件则返回step3; Step7:输出结果. 算例模拟在城市道路确定的情况下,公交线网的优化算法的仿真过程.算例中所使用的路网图如下图所示,图中一共设置了16个节点,27条路段,并假设节点1-11、8-13、2-16和13-11四对首末站.通过模型计算出优化的公交线网组合. 图1 仿真路网图 给出所有节点的OD数据、距离等基础网络数据,每一对首末站先找出最符合约束条件的距离最短的9条线路,再将其编号转为二进制,用Matlab编程软件编程,利用其中遗传算法工具箱,结合模型中的目标函数和约束条件,计算出公交线网的最优线路和组合.如图所示: 图2 遗传算法计算结果 可以得到其最优解组合路线,如下表: 表1 公交路网计算结果 本文在现有的公交网络设计研究的基础上,将公交车分为纯汽油/柴油公交车、混合动力公交车,建立了一个多目标公交网络设计模型,上层模型综合考虑了网络的时间成本、企业运营成本以及交通网络的CO2等碳排放总量三方面因素,下层模型为随机用户平衡分配模型,利用遗传算法对模型进行求解,最后用一个简单算例进行验算,从这三个方面综合考虑得出最优方案.由于影响公交出行的因素很多,模型还需考虑更多约束条件,在算法上也需进一步改善.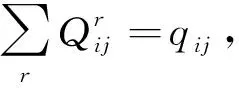
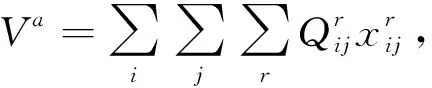
3 算法设计
3.1 编码
3.2 算法设计流程
4 算例分析

5 结束语

