两阶段混合算法的立体车库车位分配建模与仿真
王小农,李建国,张海飞
(兰州交通大学 自动化与电气工程学院,兰州 730070)
0 引 言
自动化立体车库在减轻交通压力等方面,受到认可和重视。在自动化立体车库存取车过程中,需要对车辆进行车位的分配,即选择合适的库位存取车辆,以达到减少顾客排队队长、顾客的平均等待时间以及堆垛机运行能耗过高的问题。车位的分配直接影响着自动化立体车库的运行效率以及顾客对于自动化立体车库服务的满意程度,因此,在自动化立体车库运行系统中,车位分配已经是急需解决的问题。潘耀芳等[1]通过对智能化立体车库的研究,提出了3种可提高车库效率的优化车辆存取策略,即分区存取、交叉存取和自调整策略;魏丽[2]采用基于混合编码和自适应交叉变异概率的改进遗传算法以及利用双目标优化的权重法实现优化的存取策略,对自动化立体车库的车辆存取策略算法进行了研究;吴钟鸣等[3]分析了自动化立体仓库货位优化的问题,并且采用遗传算法研究了货位优化的方法,但是采用遗传算法解决问题时,选择、交叉和变异等算子的选择使得解易陷入局部最优解;文献[4-5]介绍了巷道堆垛式自动化立体车库,其中文献[5]建立了约束条件下的车辆入库、出库、因车位存满而离去的就近存取和随机存取策略车库工作模型, 表明采用就近存取策略比采用随机存取策略堆垛机运行距离更短、能耗更低,全年能耗降低显著;左为恒等[6]采用调度堆垛机数量的传统方法下,提出一种根据车辆到达率的变化,采用调度堆垛机数量和运行速度相结合的新调度策略,从而提高立体车库的效率。大多数参考文献对立体车库效率的研究主要考虑:①堆垛机作业效率;②不同调度策略之间的结合与优化;③不同存取策略与算法的结合。立体车库效率的提升不仅需要考虑调度策略的优化和堆垛机作业等方面,还需要考虑车辆在库内的停留时间对车位分配的影响以及顾客车位优化时算法的全局搜索能力。
为了解决以上不足,本文提出基于2阶段混合求解算法的立体车库车位分配决策模型:第1阶段,利用BP(back propagation)神经网络算法预测车辆在库内的停留时间,根据不同的停留时间对自动化立体车库车位进行分区;第2阶段,车位分配时不同分区内利用果蝇算法实现车位最优分配,由于果蝇算法具有全局寻优的能力,避免了结果陷入局部最优。由于BP神经网络预测车辆在库内的停留时间会出现预测值与实际值偏差较大的情况,会影响车库的整体效率,本文分析了立体车库车辆停留时间不准确对车库效率的影响。通过比较果蝇算法与就近分配原则在实现车位分配时顾客的平均等待时间、顾客的平均等待队长、顾客的平均服务时间和堆垛机能耗效率评价指标,说明了该模型的可行性以及提高车库运行效率方面的有效性。
1 模型建立
1.1 车位分配原则
立体车库车位分配主要遵循以下6种原则。
1)车库库位受力均匀稳定性原则。质量过大的车避免集中停放,易造成车库受力不均匀,车库质心过高,导致立体车库不稳定,影响车库安全性。
2)出入库高效率原则。停放时间较短的顾客车位分配到离车库出入口较近的车位,停放时间较长的顾客车位分配到离车库出入口较远的车位。
3)先到先服务原则。根据车辆先后到达的次序,首先到达的车辆进行出库/入库服务,避免车辆发生拥堵以及延长顾客的等待时间。
4)出车优先原则。当出库顾客发出请求时,应确保出库车辆以最短的排队队长和等待时间接受出库服务。
5)堆垛机能耗最低原则。堆垛机的运行路径长度影响堆垛机能耗的多少,对车辆进行服务时应保证堆垛机从出入口到车位运行的能耗最低,达到节约资源以及降低立体车库运行成本的目标。
6)堆垛机运行时间最小原则。堆垛机的运行时间由堆垛机的运行路径决定,对车辆进行服务时应保证堆垛机从出入口到车位运行的时间最小,达到提高车库的运行效率。
1.2 车位分配的数学模型
本文针对典型的单巷道式立体车库作为研究对象,单巷道式立体车库实体模型如图1所示。
车辆到达间隔时间服从参数为λ的负指数分布,λ值表示车辆到达间隔时间的数学期望,该值越小,车辆达到频次越高。自动化立体车库存取车过程是三维立体运动,X,Y,Z方向分别为水平方向、垂直方向以及竖直方向。假设自动化立体车库有L列H行,共H×L个库位。设VL,VH分别为堆垛机Y方向和Z方向行走的平均速度,TL,TH分别为堆垛机Y方向和Z方向行走的时间,M,N,W分别为库位的长、宽、高,第i层j列库位的坐标为(j×N,i×W),那么TL,TH的值表示为
(1)
则向第i层j列库位存入或取出一辆车的时间为Tij=max(TL,TH)。
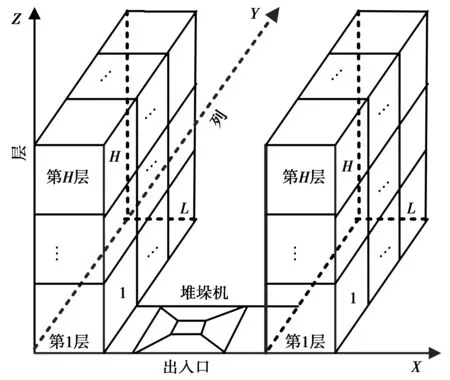
图1 单巷道式立体车库立体模型Fig.1 Single roadway stereo garage model
根据力学原理,堆垛机竖直方向和水平方向存车或取车时做功分别为
(2)
(2)式中:m表示车的质量;第i层j列库位堆垛机运动水平方向和竖直方向距离近似分别为横、纵坐标值;g是重力加速度;P为立体车库电机水平牵引功率。那么自动化立体车库车位分配优化问题可以转化为求解(3)式和(4)式的最优解
W总=min(WH+WL)
(3)
Tij=min(max(TL,TH)),1≤i≤H,1≤j≤L
(4)
1.3 立体车库评价指标和符号说明
顾客的平均等待时间T为每天接受服务顾客的等待时间之和和总的顾客数的比值,用来表征每位顾客等待时间的平均值,表示为
(5)
顾客的平均等待队长Q为每天接受服务顾客的等待队长之和与总的顾客数的比值,用来表征每位顾客等待队长的平均值,表示为
(6)
堆垛机的平均能耗W为每天接受服务车辆堆垛能耗之和与总的顾客数之比,表示为
(7)
顾客的平均服务时间S为每天接受服务的顾客的服务时间之和和总的顾客数的比值,用来表征每位顾客接受服务的平均值,表示为
(8)
(8)式中:ti为每位顾客等待的时间长;L(j)为第j位顾客的等待队长;W(i)为第i位顾客的能耗;S(j)第j位顾客的服务时间;N为总的顾客数。
2 基于神经网络算法停留时间预测的实现
2.1 神经网络算法模型
神经网络[7-8]基本组成元素是人工神经元,模型如图2所示。
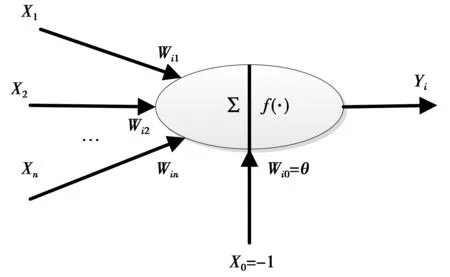
图2 人工神经元模型Fig.2 Artificial neuron model
图2中,f(·)称为激活函数。假设模型为第i个神经元,Yi为神经元i的输出,X1~Xn是从其他神经元传来的输入信号,Wij表示从神经元j到神经元i的连接权值,θ表示偏置,神经元i的输入为Xj(1≤j≤n),总输入Net(i)称为净激活,表示为
(9)
Net(i)与输出Yi之间的关系表达式为
Yi=f(Net(i))
(10)
本次仿真我们采用有导师学习BP神经网络学习算法,该神经网络属于工作过程中信号只能向前传递到达输出层,层与层之间没有向后的反馈信号。有导师学习算法的核心思想是通过将一组训练集送入网络,根据网络的实际输出与期望输出之间的差值,不断调整神经网络中神经元之间的权重,使得实际输出与期望输出之间的差值达到最小。有导师学习算法主要有以下步骤。
步骤1从样本集合中抽取一个(Oi,Ii)的样本;
步骤2计算神经网络的实际输出O;
步骤3计算输出误差C=Ii-O;
步骤4根据C调整权重向量矩阵W;
步骤5对每个样本集中的样本重复进行上述过程,直到对整个样本集来说误差不超过规定的范围则训练结束,权重向量矩阵满足所需要求。
2.2 基于神经网络算法停留时间预测的实现
BP神经网络具有将非线性数据进行映射的能力,一个3层BP神经网络对任何非线性函数可以实现逐次地逼近。本次仿真采用3层BP神经网络,以现实生活中某自动化立体车库实际运行数据中的顾客停留时间数据集作为BP神经网络的训练样本,进行BP神经网络学习。BP神经网络参数设置如下。
1)节点个数设置。输入向量的维数与输出向量的维数均为一维,故输入层、输出层的节点个数均为1。隐含层节点太少,网络性能较差;隐含层节点数太多,使得网络训练时间延长,综合考虑网络结构复杂程度以及误差大小,隐含层节点数选取为3;
2)传递函数设置。本次神经网络的训练样本均有非线性特性,故隐层函数选取S型激发函数logsig函数、输出层选取S型激发函数tansig函数;
3)训练方式。采用动态及自适应的梯度递减训练函数traingdx,其训练过程中具有学习速率可变的特点。其中,X为根据顾客到达时间产生的顾客号,Y为对应顾客在库内的停留时间。BP神经网络预测顾客库内的停留时间如图3所示,横坐标为根据顾客的到达时间车库控制系统分配的顾客号,纵坐标为不同顾客号对应的停留时间。

图3 神经网络预测顾客停留时间Fig.3 Neural network to predict customer stay time
3 基于果蝇算法车位分配的实现
3.1 果蝇算法数学模型
果蝇算法[9-10](fruit fiy optimization algorith,FOA)依照了果蝇搜寻食物的特性,果蝇优化算法的基本流程描述可归纳为以下步骤。
步骤1初始化果蝇的位置:X_axis,Y_axis;
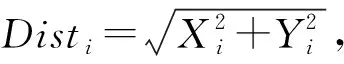
步骤3将味道浓度判定值Si代入味道浓度判定函数,从而得出表示果蝇个体自身位置的味道浓度值Smelli=Function(Si),找出此果蝇群体中味道浓度值最小的果蝇,表示为
[bestSmellbestIndex]=min(Smelli)
(11)
(11)式中:bestSmell表示最优浓度值;bestIndex表示拥有最优浓度值的果蝇的序号。
步骤4保存X,Y坐标和最佳味道浓度值bestSmell,这时果蝇通过视觉飞向该位置,表示为

(12)
步骤5进入迭代寻优,重复执行步骤2—4,比较得出的味道浓度值和前一次迭代的味道浓度值,如果前者较优,则执行步骤4。
3.2 车位分配的仿真实例
本文建立先到先服务、出车优先原则的立体车库模型,没有空余车位时,车辆离去。本次仿真假设实例为9层×21列的立体车库模型,自动化立体车库M=5 500 mm,N=2 400 mm,W=1 700 mm,堆垛机的运动速度分别为VL=3 m/s,VH=1 m/s,则Z,Y方向分别移动一个车位所需时间为1.7 s和0.8 s。车辆每吨对应水平牵引功率P为2.2 kW,由(2)式知:每吨Y方向移动一列耗能为1.246 kJ,每吨Z方向移动一行耗能为16.66 kJ。车辆的质量服从[1.1,3.5]区间内的均匀分布,车辆到达时,顾客在库内的停留时间由2.2节神经网络算法进行预测。根据顾客停留时间不同,顾客的停留时间小于或等于100 min时,车位分配在1—7列;当顾客的停留时间大于100 min且小于等于200 min时,车位分配在8—15列;当顾的停留时间大于200 min时,车位分配在16—21列。基于图1立体车库模型和车辆到达间隔时间服从参数为λ=5的负指数分布基础上随机产生200个顾客,就近分配原则下的效率指标如图4所示,基于果蝇算法进行车位分配的效率指标如图5所示。

图4 就近分配原则下效率指标Fig.4 Efficiency indicator under the principle of the nearest distribution
3.3 仿真结果分析
由图4知,采用就近分配原则顾客的平均等待时间为8.5 min、顾客的平均等待队长为5.0个、平均服务时间为9.0 s、堆垛机的平均能耗为55.0 kJ。由图5知,基于果蝇算法进行车位分配时顾客的平均等待时间为2.3 min、顾客的平均等待队长为0.33个、平均服务时间为6.7 s、堆垛机的平均能耗为35.1 kJ。相比就近分配原则,基于果蝇算法进行车位分配时顾客的平均等待时间缩短了6.2 min,顾客的平均等待队长减少4.7个,顾客的平均服务时间缩短了2.3 s,堆垛机平均能耗降低了19.9 kJ。

图5 果蝇算法模型下效率指标Fig.5 Efficiency index under fruit fly model
由此可知,采用果蝇算法进行车位分配时大大提高了车库的效率,提高了自动化立体车库进行服务时顾客的满意程度。以上自动化立体车库的仿真中利用神经网络进行车辆库内停留时间的预测,停留时间预测的准确性影响到车库运行效率和顾客对车库服务的满意度,由于实际车库运行中存在停留时间预测不准的情况,必然对顾客的平均等待队长、平均等待时间、堆垛机的能耗和车库对顾客的服务时间产生影响。以现实生活中某自动化立体车库实际运行数据中的200位顾客停留时间数据集作为2.2节BP神经网络的检验样本知:神经网络预测停留时间75%以上的情况下预测准确,能达到现实生活中的要求,25%以下的情况采用神经网络预测停留时间存在反差。
4 结 论
本文建立先到先服务、出车优先原则的立体车库运行模型的基础上,给出评价自动化立体车库运行效率的几种指标。通过比较车辆就近分配和基于果蝇算法车位分配模型下的效率指标,证明了果蝇算法进行车位分配在保证车库运行效率和降低车库运行能耗上的有效性。衡量自动化立体车库性能高低的重要指标之一是存取车的效率,而存取车的效率取决于采取合适车位分配策略,使用优化算法的分配策略能有效提高车辆出入库的效率以及顾客对自动化立体车库服务的满意度。
本文研究采用了神经网络算法进行预测顾客的停留时间,根据顾客在库内的停留时间对车位进行分区,利用果蝇算法进行了车位的分配。今后的研究中应考虑车辆的质量、车辆的出入库频率以及顾客的停留时间等对车位的影响要素进行合理分区,对车位的分区以及神经网络的参数进行优化,提高神经网络预测时间的准确性,精确的顾客停留时间预测能提高车库的运行效率。车位分配的研究中可以考虑采取多目标优化思想进行车位分区,从更加切实的角度对立体车库进行车位的分配,更大限度地使立体车库服务现代社会生活中。

