改进型单频非遍历值域姿态测量算法

权 源，赵修斌，庞春雷，王 勇，伍劭实，吴洪涛

(1.空军通信士官学校，辽宁 大连 116000； 2.空军工程大学 信息与导航学院，西安 710077)

0 引 言

随着卫星导航系统技术的迅猛发展[1]，利用GNSS对载体进行定位、定向逐渐成为一种常用手段[2]。而高精度姿态测量的关键环节在于正确解算整周模糊度[3-5]，故针对整周模糊度的快速解算关键问题产生了众多解决方法。根据观测信息的使用方式不同，可大致分为基于观测域、基于坐标域、基于模糊度域3种类型[6]。观测域类型最早由Hatch[7]提出，其核心思想是直接利用P码观测值解算整周模糊度；坐标域类型以模糊度函数法[8-9](ambiguity function method, AFM)为代表；模糊度域类型的代表算法有最小二乘搜索法[10](least squares search, LSS)、快速模糊度确定法[11](fast ambiguity resolution approach, FARA)、最小二乘降相关平差法[12](least-squares ambiguity decorrelation adjustment, LAMBDA)等。

值域法[13]本质上是一种基于坐标域解算整周模糊度的算法，它首先建立了模糊度与姿态角间的数学模型，然后通过遍历姿态域确定全体模糊度候选值。但是遍历搜索的方式会造成运算量增加，文献[14]通过构造二维姿态角与二维模糊度方程组，利用二维模糊度搜索空间压缩姿态角搜索空间，有效减少了姿态角候选数目。但该改进算法一方面未考虑到二维模糊度搜索范围对姿态角空间的重要程度，使得压缩效率较低；另一方面采用累积基线长度残差和最小准则固定整周模糊度，使得需要较多的历元数据方能消除测量误差带来的影响。

针对上述问题，本文首先基于最小二乘搜索法[15]得到全体三维模糊度搜索空间，并利用基线长度与低成本微机电系统(micro electrical mechanical system，MEMS)提供的俯仰角信息[16]对三维模糊度空间进行筛选。然后考虑到仰角越低的卫星其观测噪声越易偏离正态分布，且异常的概率也更大。为防止双差观测噪声对算法造成影响，选取其中仰角最高的3颗卫星构成二维模糊度搜索空间，并将其代入搜索模型，经MEMS再约束后解得最终的姿态角搜索空间，即解得整周模糊度候选值。改进算法由于较充分利用到基线先验信息以及低成本惯性器件提供的姿态角粗值，使得模糊度候选数目较原算法大大减少，采用残差比例检验法即可快速正确固定模糊度，算法的时效性与可靠性均得到较大提升。

1 非遍历值域算法

1.1 值域搜索模型

忽略噪声等影响，假定接收机A和接收机B同时观测到卫星i,j，A到B的基线矢量记为d，长度记为|d|，则卫星i,j对应的双差载波相位方程为

λ(φij+Nij)=(Si-Sj)d

(1)

(1)式中：λ为载波波长；φij为双差载波相位观测值；Si和Sj为卫星到接收机之间的视线矢量；Nij为双差整周模糊度。

在东北天坐标系中，取基线端点B作为坐标原点，卫星i作为参考星，基线俯仰角为θB，航向角为φB，卫星i,j的航向角和俯仰角分别为(φi,θi),(φj,θj)，则 (1) 式可改写为

(2)

由(2)式可知，通过二维遍历姿态角即可解得与之对应的模糊度浮点解，就近取整后得到全体整周模糊度候选值。

1.2 压缩搜索空间

值域搜索模型通过建立模糊度与姿态角之间的数学模型，以姿态角作为中间量解得全体整周模糊度，但遍历搜索的方式会降低搜索效率，由于该数学模型本质是通过二元自变量推导一元因变量。若已知二维模糊度搜索空间，可构造二元模糊度和二元姿态角方程组，从而利用模糊度域压缩姿态角域。

首先，将(1)式改写为

(3)

(3)式中，ed=d/|d|，eij=Si-Sj/|Si-Sj|，由 (3) 式可推知

(4)

(5)

由(5)式可以确定二维整周模糊度(Nij,Nik)取值范围，根据模糊度与姿态角之间的内在关系构造二元一次方程组

(6)

对任意一组(Nij,Nik)，对(6)式采用解析法[17]即可解得对应的俯仰角θB与航向角φB，然后将解得的姿态角代入(2)式得全体候选模糊度浮点解。

1.3 固定整周模糊度及姿态解算

将全体模糊度浮点解就近取整后，分别代入(1)式解得对应不同时刻的基线矢量x，判定使得目标函数(7)成立的整周模糊度为最终解。

(7)

固定整周模糊度后，将其代入(1)式解算高精度基线矢量d，设d在东北天坐标系的坐标为(de,dn,du)，可得航向角φB和俯仰角θB分别为

(8)

2 改进算法

由(5)式可知，二维模糊度空间是由2组一维模糊度通过排列组合形成的。但这种方式会造成二维模糊度搜索数目较多，进而影响姿态角搜索数目，造成模糊度候选解冗余，不利于判定正确的整周模糊度。

由于模糊度组中仅含有3个线性无关的模糊度，且利用这3个线性无关的模糊度即可解算基线矢量，结合基线先验信息对模糊度搜索空间进行压缩，其结果等价于压缩了模糊度候选空间的大小。

2.1 最小二乘搜索法

首先选取仰角最高的4颗卫星(其中一颗为参考星)构造三维双差整周模糊度搜索空间，其矢量形式可表达为

(9)

若已知三维整周模糊度(N21,N31,N41)中每一维的取值范围，对三维模糊度全排列组合后即得到三维模糊度搜索空间，将其代入(9)式解算全体基线矢量候选值(de,dn,du)，然后得到对应的基线几何长度与姿态角粗值，并以此筛选模糊度空间。

2.2 筛选三维模糊度空间

首先利用(5)式单独求解每一维度的模糊度，以建立三维模糊度基本搜索空间，为降低模糊度候选数量，本文首先利用基线长度信息对三维模糊度搜索空间进行粗筛选。

将(9)式改写为矩阵形式

A-1λ(φ+N)=d

(10)

(10)式中，

|d|2=YTA-TA-1Y

(11)

令G=A-TA-1，对其进行Cholesky分解得

G=LTL

(12)

(13)

由于利用(13)式解得的模糊度搜索数量依旧较多，故按以下步骤进一步压缩数量。

步骤1基线长度约束。由(9)式解得基线矢量后，利用基线长度信息已知，可以排除部分错误解，一般取误差ε1为基线长度1%～2%。

(14)

步骤2MEMS辅助约束俯仰角。美国MicroStrain公司生产了一款基于MEMS传感器技术的高性能微型捷联航姿系统，某款型号为3DM-GX3-25捷联航姿系统由三轴加速度计、三轴陀螺仪、三轴磁强计、温度传感器组成，可提供静态、动态的定向以及惯性测量数据(加速度、角速率、磁场、角度偏差、速度偏差矢量等)，三轴加速度计可提供俯仰角信息，且其漂移是周期性的，故可为提供俯仰角粗值信息。

设由MEMS输出得到的俯仰角为θMEMS，在满足(14)式的基线矢量中，保留使得(15)式成立的基线矢量对应的三维整周模糊度组，然后选取仰角最高的3颗卫星对应的整周模糊度作为二维模糊度搜索空间，将其代入(6)式解算姿态角搜索空间，进而解得整周模糊度候选值。

(15)

2.3 固定整周模糊度

确认模糊度可采用多种固定准则，如：基线残差累积平方和最小准则、整周模糊度特性准则、残差比例法等等，这些准则目的均是从模糊度候选空间中判定出一组正确值，故需要满足2个条件：①模糊度候选空间中包含正确解；②空间内“危险”的错误候选值尽可能少。

由于(5)式中必然包含正确的整周模糊度，故将(6)式解得的姿态角代入(2)式后，可解得包含正确解的模糊度候选空间，满足第一个条件。

由于姿态角候选值与模糊度候选值存在映射关系，故姿态角数量越多，则模糊度候选空间越大，存在“伪解”的可能性越大，而经过基线长度以及MEMS约束后的姿态角候选空间必然有所减少，有利于排除部分错误解，增强模糊度候选空间稀疏性，最终减少模糊度确认过程所需时间。

假设已知一组整周模糊度真值，将其带入双差载波相位方程可知

(16)

(17)

ΔL-λK→0

(18)

(18)式中，K与ΔL同维。λ越小，(18)式越容易成立，即符合精度标准的模糊度越多。λ越大，符合精度标准的模糊度越少。由于约束后的模糊度候选空间元素减少，等同于λ增大，即减少了高精度估计结果的模糊度候选值数量，而模糊度候选空间稀疏性越强，次优解残差则越大(排除了部分伪解)，对应的残差比值也更易通过统计检验。故采用残差比例检验法准则代替原算法的基线残差累积平方和最小准则，从而完成模糊度固定过程。

残差比例检验法的基本思想是：首先将全体模糊度候选值代入双差载波方程式中，解得对应的基线矢量，然后以模糊度与基线矢量作为已知量得到双差载波相位计算值，将计算值与测量值进行运算得到残差平方和Ω，比较最小残差平方和Ω1与次小残差平方和Ω2之间的比值，判定使得Ω2/Ω1>χ成立的最小残差平方和对应的整周模糊度为正确解。

改进算法流程如图1所示。与原算法相比，改进算法基于最小二乘搜索算法，结合基线先验信息与MEMS提供的俯仰角信息对二维模糊度搜索空间进行压缩，搜索数目的减少有利于增强模糊度候选空间稀疏度，使得正确模糊度对应的残差比值更易通过统计检验。

图1 改进算法流程图Fig.1 Flow chart of the improved algorithm

3 试验结果及分析

3.1 试验条件

以学院操场作为本次试验地点，将2台接收机分别连接在基线两端，将MEMS测量单元固定在基线中央，Y轴与基线矢量平行，其性能参数在静态条件下俯仰角偏差为±0.5°,动态条件下偏差±2°。事先已测得基线长度为1.907 m，俯仰角和航向角分别为0.1°和229.15°，将其作为真实值与实验组进行参照对比。采样频率设为1 Hz，可见卫星编号按仰角大小依次为31#, 32#, 14#, 25#, 3#, 16#, 29#, 20#，其仰角分别为64.5°，52.8°，52.2°，27.2°，24.5°，20.5°，18.7°，15.1°。在基线静止的情况下，将LAMDA算法经过长时间观测解得的整周模糊度视作真值，其具体为8 388 608，8 388 613，8 388 609，6 626 617，6 626 615，6 626 631，6 626 635。

3.2 试验过程

假定方案1为原算法，方案2为本文改进算法，方案3将原算法的固定策略变更为残差比例检验法，方案4将改进算法的固定策略变更为累积基线残差平方和最小准则。

首先，对比由LAMBDA算法、原算法以及本文算法解算得到的整周模糊度，三者结果相同，可见改进算法压缩搜索空间的同时保证了搜索空间的正确性。

然后，比较各方案搜索空间大小。方案1的二维模糊度搜索空间数目为16×19=304组，方案2首先解算全体三维模糊度搜索空间，然后利用MEMS提供的俯仰角以及基线长度对其进行筛选，使得最终模糊度空间数目筛选至5组，可见，较方案1的搜索空间数量显著减小，以模糊度N21，N31，N41为例，由于原模糊度值过大，无法在图中判断是否存在1周左右变化，故将前3个模糊度整体减去8 388 600，得到“新”模糊度8，13，9，分布如图2所示。

图2 不同方案的模糊度搜索数目Fig.2 Searching number of ambiguity in different cases

当解得二维模糊度搜索空间后，将其代入(6)式解算姿态角搜索空间。对比可知，方案2的姿态角空间数目由先前的576组降至8组，如图3所示。

确定姿态角搜索空间后，将其代入(2)式解算得到模糊度候选解，下面从不同角度对改进算法性能进行分析。

图3 不同方案的姿态角搜索数目Fig.3 Searching number of attitude angle in different cases

对比方案1与方案4，由于原算法模糊度候选数目较多，故采用累计基线残差平方和最小准则作为固定策略时模糊度固定所需历元数随之增多，而改进算法与原算法相反，使得其在某些时刻甚至可单历元成功固定，如图4、图5所示。

图4 方案1的模糊度收敛过程Fig.4 Convergence process of the ambiguity in case 1

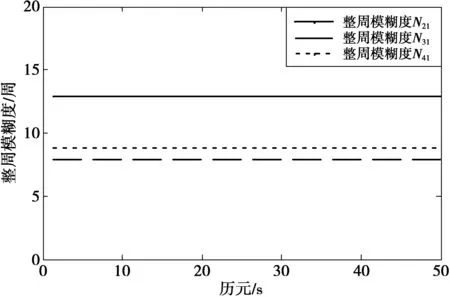
图5 方案4的模糊度收敛过程Fig.5 Convergence process of the ambiguity in case 4

由于该固定策略极易受到历元噪声的影响，且不易判定是否解得正确的整周模糊度。故采用残差比例检验法进行模糊度确认，本文从各历元最小残差对应的整周模糊度以及对应的残差比值2个方面，对方案2、方案3进行对比(取残差比例检验法的阈值为2，由于个别历元残差比值过大，为观察所有历元的残差比值情况，对残差比值作log化处理)，如图6—图9所示。

图6 方案3的各历元模糊度固定情况Fig.6 Fixed ambiguity in case 3

图7 方案3在各历元解得的残差比值Fig.7 Ratio of residual error in case 3

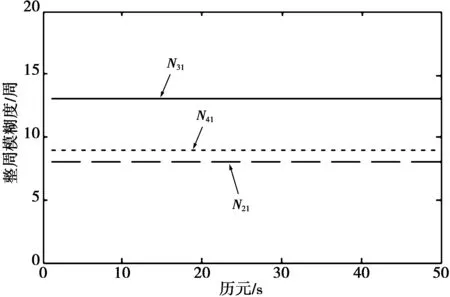
图8 基于方案4的各历元模糊度固定情况Fig.8 Fixed ambiguity in case 4

由图6，图7可知，由于原算法模糊度候选数目较多，导致单历元模糊度固定成功率不高，若将残差比值取2作为检验阈值会导致漏检甚至误判的情况发生。

由图8，图9可知，由于改进算法模糊度候选数目较少且模糊度候选空间的稀疏度较高，使得单历元模糊度固定成功率近100%，且各历元残差比值均大于2(残差比例峰值可达127 9)，而残差比值越大，模糊度固定结果的可靠性越高。

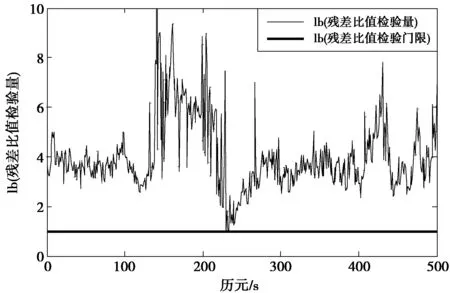
图9 基于方案4在各历元解得的残差比值Fig.9 Ratio of residual error in case 4

4 结束语

本文在非遍历值域算法的基础上，对模糊度候选值数量有着决定性影响的二维模糊度搜索空间解算方法进行了改进，在已知基线长度与MEMS提供的俯仰角信息基础上，排除部分错误解以及“危险”解，使得模糊度候选解数量较原算法大大减小，实现了单历元解算整周模糊度。