非平稳信号实时谱分析算法及其FPGA实现

周 围，梁 琦

(1.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065; 2.重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

在工业监控领域，通过对旋转设备中与轴旋转频率相关的振动信号与噪声信号功率谱特征进行分析来判断旋转机电设备的运行情况并进行实时故障检测是十分有效的方法[1]。在电力系统中，通过对电源信号进行谱分析能够实时测量由于大负载(如：电动机、焊接机)接入或开机运行产生的电压失真、抖动和不平衡[2]。在频谱监控领域，如感知无线电中通过动态频谱接入和快速频谱感测技术实时检测用户是否存在[3]。因此，谱分析是大多数学科中的一个重要任务，且其主要目的是功率谱测量。传统的谱分析方法一般采用基于快速傅里叶变换(fast Fourier transform,FFT)及其改进算法和频谱细化分析法。FFT算法得到的是整个频带的粗略全景谱，频率细化算法可以得到频谱的局部详细特征。但由于上述方法只能分析统计平均结果，因此均适用于平稳信号的谱分析，而无法处理非平稳信号。实际观察到的信号(如振动信号)大都为非平稳信号，对其非平稳性的分析可以实现故障的实时诊断、排除和频谱实时监控。非平稳信号典型的处理方法有短时傅里叶变换、Wigner-Ville分布、Gabor变换、小波分析和分数阶傅里叶变换。考虑硬件实现复杂性和实时性，工程上一般采用短时傅里叶变换。为克服短时傅里叶变换的频率分辨率完全受限于滑动窗口长度和其无法分析局部频谱的缺陷。本文拟采用窗口长度逼近平稳信号的观察窗采样非平稳信号，然后利用多相滤波器得到分析频带重构信号，之后通过加窗线性调频Z变化(chirp Z transform,CZT)实现与时间分辨率无关的频谱细化，最后利用累加平均与谱分析解决旁瓣误差和噪声误差，并利用FPGA(field-programmable gate array)硬件实现。

1 输入输出描述

图1为本设计的全局视图。图1中，fmin和fmax分别为谱分析起、止频率；Ns为分析带宽内最大信号数目；Δf为频率分辨率和IDR(instantaneous dynamic range)(单位：dB)为瞬时动态范围。假设输入平稳信号由R个信号组成，采样窗口内非平稳信号由R个能量集中的窄带信号组成，在此假设的基础上每个窄带信号可以作为一个复数基。则

(1)

图1 频谱分析仪全局视图Fig.1 Global view of spectrum analyzer

对信号进行谱分析并将各时刻检测到的信号数目、各信号中心频率和功率封装为信号描述字(signal description word,SDW)。通过SDW的运用将分析带宽内包含的谱信息简化为一个描述字方便用户应用。

2 关键模块理论分析

2.1 CZT算法原理

设通过ADC采样信号为x(n)(n=0,…,N-1)。根据文献[4]可知，其Z变换可表示为

(2)

(2)式中：f(n)=x(n)A-nWn2/2；h(n)=W-n2/2，其中，A=A0eiθ0,W=W0e-iφ0。A0为z平面上起始点幅值，θ0为起始点相位(对应起始点频率)，W0为幅值变化梯度倒数，φ0为相位增量(对应频率分辨率)。A0=W0=1，使CZT变换路径为单位圆上的一段圆弧，令M=N(M为谱线数)简化CZT计算复杂度，通过θ0调整起始频率，通过φ0确定选频范围内细化倍数。

(2)式的计算可通过图2所示步骤来实现。

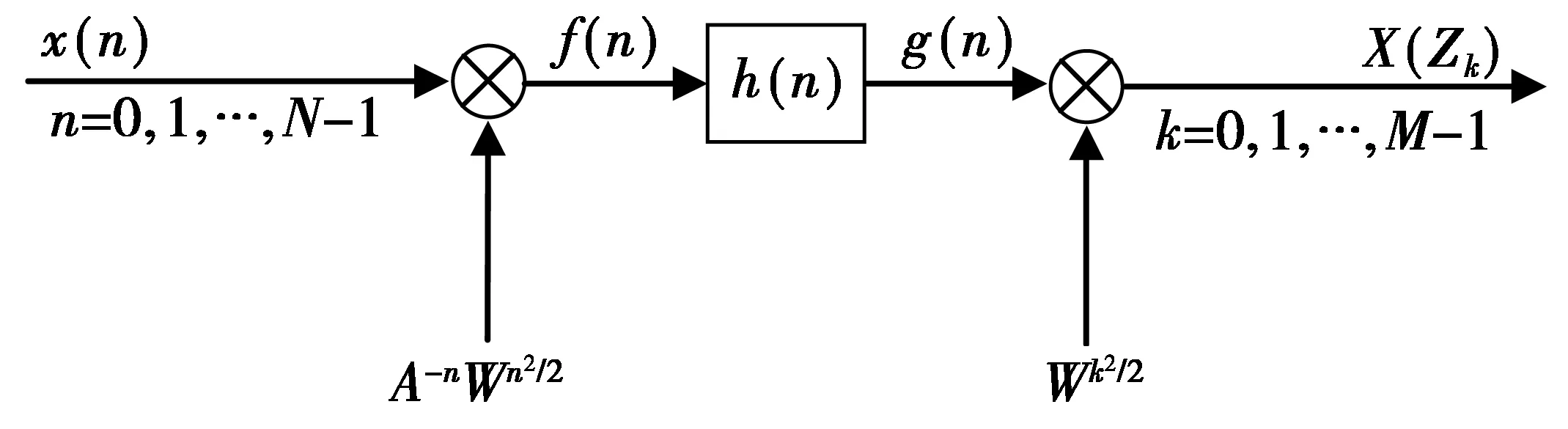
图2 CZT计算框图Fig.2 Block diagram of CZT calculation

图2中，f(n)与h(n)的离散卷积可通过其循环卷积实现。

2.2 窗函数选择原理

窗函数的选择是确保该算法成功应用的最关键部分。系统归一化的频率分辨率可表示为

(3)

(3)式中，D为频率细化倍数。则窗函数必须满足下述条件。

1)窗函数旁瓣电平(side lobe level,SLL)需满足SLL>IDR。否则将无法满足用户输入IDR的要求。

2)窗函数6 dB带宽需满足：BW-6 dB<Δfb。在满足Δf要求下，为正确区分2个同功率信号，采用文献[5]中的典型标准BW-6 dB<Δfb。

3)窗口幅值下降IDR(dB)带宽需满足：BW-IDR<2Δfb。为保证Δf适用于更大的IDR，IDR对应的窗口宽度必须比2Δfb更窄。

为准确检测Ns个信号，在此考虑最坏旁瓣条件(即输入信号为Ns-1个同功率信号和一个满足IDR的最小功率信号)，则此时窗函数应满足(4)式条件。

SLL>IDR+20lg(Ns-1)+SL

(4)

(4)式中：Ns>1；SL为窗口扇形衰落即当信号频率为2个CZT频率点中间时的功率损耗[5]。

根据IDR的要求，归一化频率分辨率可表示为

(5)

(5)式中，BWnull为窗函数主瓣宽度。

对于非平稳或瞬态信号的分析，窗函数除满足上述频域要求外还应根据时域分辨率和最小检测信号长度的要求选择适合的采样窗长度及重叠帧数。

2.3 谱分析算法原理

为实现降低测量误差，得到更精确的测量结果，本文设计了3个阈值参数。该部分对各阈值参数设置理论进行了详细阐述，具体参数示意如图3所示。

图3 阈值参数示意图Fig.3 Schematic diagram of threshold parameter

1)窗口主瓣宽度nb：为了简化硬件实现将加窗后信号主瓣假设为由奇数点CZT分辨率点组成，nb=2|BWnull/2|+1。避免了若nb为偶数时为降低错误检测概率消除信号两侧nb/2点还是(nb-1)/2点。

2)噪声阈值T(单位：dB)：为了避免由噪声引起的测量误差，在此引进噪声阈值T(单位：dB)。根据文献[6]定义

(6)

(7)

当M≫1时，将(7)式代入(6)式得

PFA|M≫1≈e-γ

(8)

此时，PFA检测性能趋于(6)式理论值。

若谱线数为MCZT点，且其服从独立同分布，则

(9)

根据(8)，(9)式可得

γ≈-ln(PFA,g/MCZT)

(10)

3)动态阈值S(dB)：为保证IDR的要求，避免由于窗函数旁瓣造成的检测误差，设定动态阈值S=IDR+SL，其中，SL为窗函数的扇形衰落。

2.4 多相滤波原理

图4为子带设计示意图。设系统采样率为fs，将其划分为N个等间隔子带，则第i个子带的中心频率为ωi=2πfi/fs。设计任何相邻子带的阻带截止频率为对方的中心频率，且子带间中心频率间隔f1满足f1=mΔf(m为正整数)[7]。

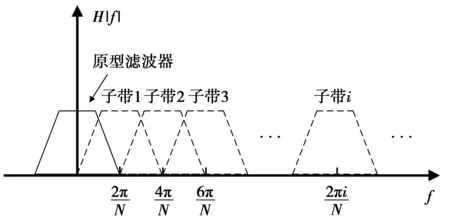
图4 子带划分示意图Fig.4 Diagram of subband division

原型滤波器传输函数为

(11)

(11)式中M为滤波器长度，设子带i系数函数为

(12)

(12)式中WN=ej2π/N，则子带i传输函数可表示为

(13)

3 FPGA设计实现

本文设计谱分析仪期望在算法与硬件实现上高度可配置，因此，设计时必须考虑多参数组合。在此以表1中2个实例介绍本算法内部参数计算过程。

表1 设计实例用户输入参数

1)根据用户输入IDR=30 dB，Ns=4，由(4)式可知，SLL≥40。在此，窗函数选择Hamming窗(根据文献[5]可知，Hamming窗SSL=-43 dB，SL=1.78 dB和主瓣点数=4)以满足IDR要求，且nb=5，S=33。根据起止频率与系统采样率得D=16，根据归一化分辨率公式、频率分辨率及(5)式得NCZT=M=512。由起始频率与初始相位对应关系和NCZT=512得θ0=2π×fmin/fs=2π·35/512。

2)同理可知，在此需选用Blackman-Harris窗，且nb=9，S=78，D=4，NCZT=M=512和θ0=2π·77/512。

图5为谱分析仪系统结构图，由3个部分组成。硬件实现的关键问题是模块间的跨时域传输和模块内的流水线处理，因此，本文通过系统延时分析确定各时钟域时钟频率。下面将对谱分析仪各主要模块的硬件实现进行详细叙述。

3.1 滤波器组实现

为使滤波器满足实时性和固定数目子带划分要求，原型滤波器(抗混叠滤波器)需选用运算量小且截止频率与采样率相关的滤波器。因此，本设计采用整系数升余弦滤波器实现。

首先利用Matlab设计实现升余弦滤波器并导出其系数，根据(12)式计算出各子带滤波系数。然后将上述滤波系数存入相应ROM(read only memory)中，并通过与采样数据乘累加实现滤波功能，对滤波结果进行移位实现归一化处理。为达到测量精度与实时性能的平衡，平稳信号与非平稳信号原型滤波器带宽分别为fS/20和fS/50。滤波器组实现结构如图6所示。

图5 系统硬件框图Fig.5 Block diagram of system hardware

图6 多相滤波器结构图Fig.6 Structure diagram of multiphase filter

3.2 CZT实现

根据图2算法流程可知，该算法核心为f(n)和h(n)的卷积。由傅里叶变换卷积定理可知循环卷积可通过FFT快速计算[8]，计算流程如图7所示。

根据CZT原理可知，产生信号与用户输入起始频率、终止频率、细化倍数和输出谱线数有关，因此信号产生可通过2个DDS(direct digital synthesizer)模块和一个数据缓存RAM实现。为提高系统运行速率将2个DDS模块与2个FFT均采用并行架构实现，为节约资源提高芯片利用率将复数乘法器复用并将FFT1复用至FFT3。此时FPGA实现CZT模块数据流如图8所示。

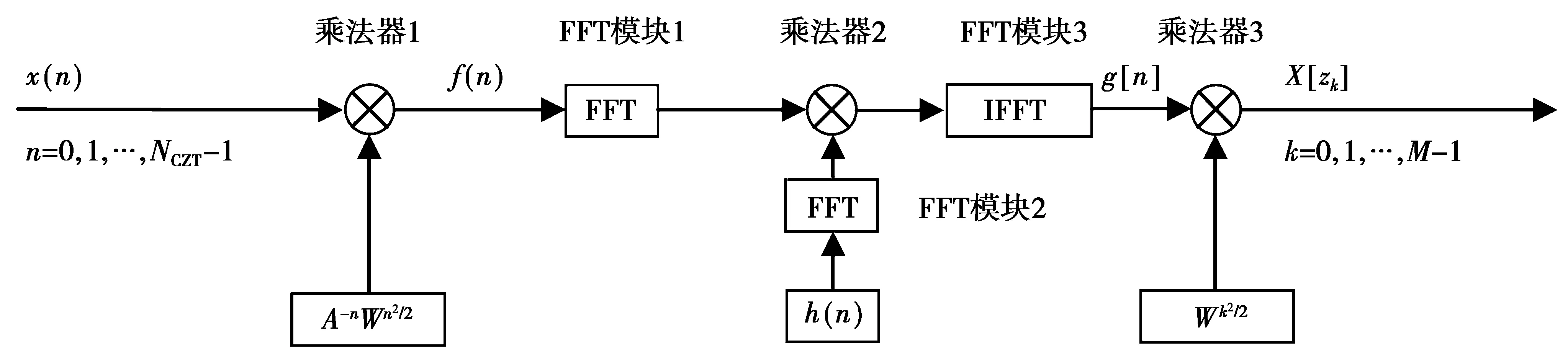
图7 FFT实现循环卷积CZT流程Fig.7 FFT implementation of the convolution CZT process

图8 CZT算法硬件实现数据流图Fig.8 CZT algorithm hardware implementation data flow diagram

图9 频谱分析结构框图Fig.9 Structure diagram of spectrum analysis

3.3 谱分析实现

通过对CZT模块输出数据进行累加平均降低瞬态误差，将累加平均结果通过频谱分析得到SDW。具体实现步骤如图9所示。

累加模块在FPGA中通过2个移位寄存器与加法器实现多个功率谱对应位置数据的累加。累加谱数量由用户输入参数决定，为提高系统运行速率将其设为2的整数次幂，则平均可通过移位实现。

创建2个长度为Ns的存储器，分别存储功率值和对应数据位置。则谱分析可通过下述步骤实现。

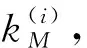
2)噪声估计。噪声功率为不考虑与上述Ns个信号相关的输出功率平均值：

(14)

(14)式中，Ms=M-nbNs，b[k]为空白窗,即

(15)

4)SDW产生。将分析带宽内信号数ND、信号检测频率和功率通过输出端口输出。

3.4 系统时延

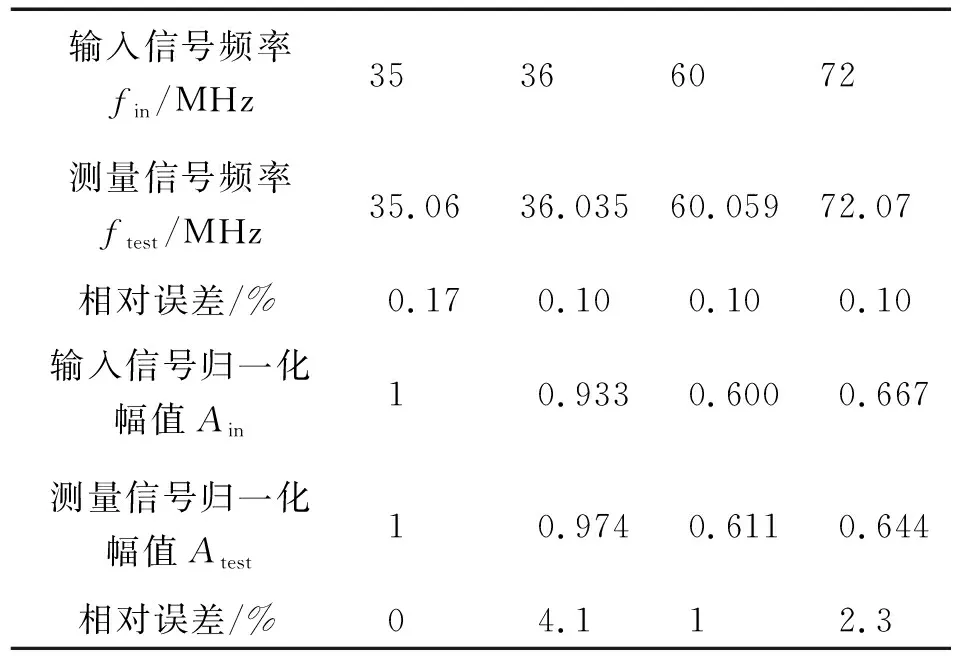
图10为谱分析仪数据流结构。在此定义2个概念：块延时lB(数据帧进入系统的时间间隔)和总延时lT(从第一个数据进入到SDW输出时间间隔)。根据图10可知，lT=lFIR+lCZT+lPA，因此,lB

(16)

图10 谱分析仪时延示意图Fig.10 Schematic diagram of spectrum analyzer time-delay

多相滤波模块以采样率fs连续处理数据并将结果存入缓存RAM，因此，该模块的延时与块延时相等即lFIR=lB。当第1个数据块通过多相滤波模块时，CZT模块将开始处理数据，因此，CZT模块必须在下一个数据块完成多相滤波之前处理完该数据块，即lCZT≤lFIR。CZT模块的延时由10个周期地址运算时延、3个周期复数乘法器、2·NCZT个周期缓存时延和2·NCZT个周期IFFT时延组成，lCZT可表示为

(17)

(17)式中，fCZT/2由FFT的结构决定。

在CZT模块加载新的一组数据之前，谱分析模块应完成上一组数据处理，即lPA≤lFIR。谱分析首先需要将CZT模块输出数据加载到谱分析模块，再对NCZT点CZT输出结果中进行Ns次最大值搜索，一次噪声估计和280个时钟周期的其他处理(谱调整及SDW生成)。因此，谱分析延时lPA可表示为

(18)

通过上述各模块延时分析可知lT≤3·lFIR。

4 系统验证

在此部分将对设计谱分析仪在平稳信号和非平稳信号实时分析方面性能进行验证，硬件平台选用Altera Cyclone IVE:EP4CE115F29I7 FPGA。

4.1 平稳信号性能验证

为验证本设计系统在不同用户输入参数组合下测量性能，在此仿真表1中2个实例进行系统性能验证。在实例中选择各缓冲延时周期为NCZT个样点周期。

实例1对于高采样率高频率分辨局部谱分析。根据分析带宽和滤波器子带带宽，在此实例中选择子带2，3和4，为满足谱分析性能约束需对CZT模块与PA模块的时钟进行适当设置。

根据文献[9]可知，FFT模块最大频率fFFT=400 ΜΗz，因此，fCZTmax=400 MHz。由(16)式可得，lFIR=lB=15.36 μs，由(17)式和CZT模块时序约束可得fCZTmin=268 MHz，由(18)式和谱分析模块时序约束可得fPAmin=212 MHz。为降低系统功耗并保证信号流实时处理，根据fCZTmax=400 MHz,可得fPAmax=250 MHz。以fCZT=400 MHz，fPA=250 MHz配置CZT和PA模块，此时系统延时lT=38.27 μs。

设输入平稳信号x1(i)表达式为

(19)

(19)式中，f1=8 MHz；f2=9 MHz；f3=10 MHz；f4=12 MHz和fs=100 MHz。其Modelsim时序仿真所得波形图如图11。

由图11所得检测信号频率值和功率值。输入信号与检测信号频率和归一化功率值如表2所示。

图11 实例1时序仿真波形图Fig.11 Timing simulation waveform of example 1

表2 实例1信号测量结果对比

实例2对于高采样率较低频率分辨局部谱分析。同理可知，选择子带为4，5，6，7，8，9，lFIR=15.36 μs，fCZTmin=268 MHz，fPAmin=174 MHz。满足要求的时钟频率配置如表3所示。在此选用fCZT=400 MHz和fPA=250 MHz配置CZT及PA模块时钟，此时系统总延时lT=lFIR+lCZT+lPA=36.225 μs。

表3 实例2满足连续实时处理时钟频率

设输入平稳信号x2(i)表达式为

(20)

(20)式中：f1=35 MHz；f2=36 MHz；f3=60 MHz；f4=72 MHz和fs=200 MHz，其Modelsim时序仿真所得波形图如图12所示。

由图12所得检测信号频率值和功率值。输入信号与测量信号频率和归一化功率值如表4所示。

图12 实例2时序仿真波形图Fig.12 Timing simulation waveform of example 2

表4 实例2信号测量结果对比

4.2 非平稳信号性能验证

为验证本文实现系统具有非平稳信号谱分析性能，对其进行测试。设一个非平稳信号f(i)，分析带宽为0～30 MHz，每个子带最多能量集中点为3，f(i)表达式为

(21)

(21)式中，信号频率为f1=1 MHz，f2=9 MHz，f3=20 MHz和fs=250 MHz。为保证频率分析精度和实时性要求，在此采用8倍细化512点CZT，每CZT周期窗口时移样点数为52，各缓冲器延时为NCZT个样点周期。

根据分析带宽和滤波器子带带宽，在此选择子带1，2，3，4，5和6。lFIR=12.288 μs，fCZTmin=335 MHz和fPAmin=169 MHz。满足要求的时钟配置如表5所示。配置CZT和PA模块时钟频率分别为400 MHz和250 MHz，此时系统延时lT=lFIR+lCZT+lPA=31.098 μs。

表5 非平稳分析满足连续实时处理时钟频率

其Modelsim时序仿真所得波形图如图13所示。

时频分析结果如图14所示。

通过图13和图14可得各信号频率、功率和出现时刻(二者所含信息相同)。具体检测参数如表6所示。

本设计检测时间由计算时延和重叠帧时延组成，其中，计算时延可通过减少重叠点数和提高系统频率与采样率比值降低。通过表6可知，本设计对非平稳信号检测具有很好的实时性能和准确度。

图13 非平稳信号时序仿真波形图Fig.13 Timing simulation waveform of non-stationary signal

图14 Modelsim检测结果时频图Fig.14 Modelsim test results time-frequency diagram

5 与其他实时谱分析仪比较

表7对比了不同实时谱分析仪在核心算法、频点数、实时带宽(最大分析带宽)、最小频率分辨率(最大实时带宽下)、近似成本和是否可分析非平稳信号方面的异同。通过分析可知,本设计系统在实时带宽和最小频率分辨率方面具有与安捷伦和泰克实时谱分析仪相近的性能，且都可以对非平稳信号进行分析，因此在分析信号基本谱信息应用场合具有更高的性价比。同另外2种基于FPGA的实时谱分析仪相比，本设计的谱算法具有更优越的性能，且成本相近。

表6 非平稳信号测量结果对比

6 结 论

本文在结合短时傅里叶变换对非平稳信号的分析方法和CZT算法优点的基础上，针对平稳信号及非平稳信号功率谱的实时测量，提出了一种基于多相滤波原理、CZT变换和谱分析相结合的便于硬件实现的实时谱分析方法，并利用FPGA平台对该方法硬件实现。该方法利用多相滤波重构用户关注谱，利用CZT频谱细化算法解决了窗口长度对频谱分辨率的限定，谱分析算法提供了精确的谱分析结果。仿真结果及误差分析表明,该系统可准确检测平稳信号并对其进行谱分析，检测频率误差小于0.6%、功率误差小于4.5%和各实例系统最小延时均小于37 μs。而对于长度为32.768 μs非平稳信号该系统最大频率检测误差为94 kHz(频谱分辨率为61 kHz)，最大时间检测误差为0.836 μs,最大时间延时为69 μs (重叠样点为460点)，最小时间分辨率和频率分辨率可分别为1.66 μs和40.69 kHz。仿真分析表明本设计对于平稳信号及非平稳信号谱分析都具有很好的检测准确度、时频精度和实时性。

表7 不同实时谱分析仪对比