线性空间中函数的单位分解性
罗炯兴,刘焕文
(1.西昌学院少数民族预科教育学院,四川西昌615000;2.浙江海洋大学船舶与机电工程学院,浙江舟山316022)
0 引言
在文中,若函数的全部求和恒等于1,称函数满足单位分解性;把与此性质相关的定理称为函数的单位分解定理。现在,数学研究的许多问题主要的并不涉及单个对象,如一个函数、测度或算子,而是处理一大类型这种对象。在这方面出现的大多数有价值的类实际上是具有实数域R或复数域C上的线性空间,由于极限过程在每个解析问题里(明显或隐蔽地)起作用,因此,这些线性空间都可能配备度量,或者至少是拓扑,然后,从度量和拓扑的角度来考虑线性空间中的相关问题。
众所周知,在实数域R上的n维线性空间X中定义一个范数,可以使之成为一个赋范空间、度量空间和拓扑空间,通常称为赋范线性空间。目前关于赋范线性空间研究的课题和方向有很多,例如等距线性延拓问题[1-3],一般范数的正交关系[4-7]等问题。除此之外,还能够在线性空间中建立一个微分结构,使之成为一个微分流形。微分流形是一类重要的拓扑空间,它除了具有通常的拓扑结构外,还添上了微分结构,现代微分几何的研究是建立在微分流形框架上的。在微分流形的的观点下,可以认为古典微分几何中二维欧氏空间R2中的曲线是一维微分流形,三维欧氏空间R3中的曲线和曲面分别是二维、三维微分流形。
在线性空间X中应用微分流形,可以研究线性空间的某些重要性质.如对于实数域R上n维线性空间,对于所有m维子空间组成的集合,能够利用矩阵中的一般线性群GL(m),建立一个微分流形,称之为Grassmann流形G(m,n)。这样,可以从研究Grassmann流形G(m,n)来间接研究n维线性空间X的性质。文献[8]在欧氏空间Rn构造了Clifford代数Cl8的不可约表示空间,文献[9-10]利用示性类及微分几何的方法证明了定向Grassmann流形G(2,n)的上同调可以用它上面的典范失众的Euler类生成,给出了线性空间X中侵入定向曲面的Gauss映射g:X→G(2,n)在同调群上的表达式,等等。
目前,已经有许多国内外专家和学者[13-16]研究了定义在闭区间[0,1]上的任意连续函数,可以分解为两个连续函数之和,且这两个函数的图像的Hausdorff维数大于等于1,小于等于2。但这些研究结果只是针对于实数域上的闭区间[0,1]上的连续函数,换言之,将问题限制在一维线性空间范围之内,并且使用的方法有一定的局限性,难以推广应用到二维及二维以上线性空间,甚至更一般的赋范空间或者拓扑空间。
文中指出实数域R上的n维线性空间X是满足第二可数公理的n维流形,应用微分流形指出在线性空间X中存在满足单位分解的一簇光滑函数,给出了一个关于函数的单位分解定理。更进一步,对于二维线性空间X上的任意开凸体A应用单位分解定理,指出了存在定义在A上三个连续函数g1,g2和g3,满足且对任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中,i=1,2,3。这样将线性空间与微分流形相结合,为研究线性空间,甚至赋范空间和拓扑空间的函数分解一般问题及其相关问题提出了一种新方法,有助于解决问题。
1 预备知识
现在,介绍微分流形的基本定义和概念,以及单位分解定理。
定义1.1[11]设M是一个Hausdorff拓扑空间,若M的每一点p都有一个开领域,使得U和n维欧氏空间Rn中的一个开集是同胚的,则称M是一个n维拓扑流形,简称为n维流形。换言之,所谓n维流形就是在它的每一点的一个领域内可以建立n维局部坐标系的Hausdorff拓扑空间。
定义1.2[11]设M是一个n维拓扑流形,(U,φ)和(V,y)是它的两个坐标卡。若当时,φ°y-1,y°φ-1都是Cr的(其中r是正整数,或∞,或ω),则称坐标卡(U,φ)和(V,y)是Cr相关的。
定义 1.3[11]设M是n维拓扑流形,假定是M的坐标卡的一个集合,并满足以下条件:
(2)属于Λ的任意两个坐标卡都是Cr相关的;
(3)Λ是Cr极大的,即:如果假定(U,φ)是M的一个坐标卡,且(U,φ)与Λ中的每一个成员都是Cr相关的,则(U,φ)必属于Λ。
此时,我们称坐标卡集Λ为流形M上的一个Cr微分结构;当r=∞时,Λ称为M上的一个光滑结构;当r=ω时,Λ称为M上的一个解析结构。
定义1.4[11]设M是n维拓扑流形,若在M上指定了一个Cr微分结构Λ,则称(M,Λ)为一个n维Cr微分流形,属于Λ的坐标卡(M,Λ)称为该微分流形的容许坐标卡。
当r=∞时,称(M,Λ)为光滑流形;当r=ω时,称(M,Λ)为解析流形。
现在,给出光滑流形M上光滑函数及其支撑集的定义。
定义1.5[11]设是定义在光滑流形M上的连续函数,若存在M的一个容许坐标卡(M,φ),使得x∈U,且是在点φ(x)处光滑的函数,则称函数f在点x处是光滑的。若f在每一点x∈U都是光滑的,则称函数f是流形M上的光滑函数。
定义1.6[11]设是定义在光滑流形M上的连续函数,所谓f的支撑集是指f取非零值的点的集合的闭包,记作Supp f,即
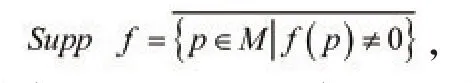
支撑集Suppf的补集是M中使f=0的最大的开支集。
称M满足第二可数公理,是指M的拓扑中一个拓扑基是一个可数簇。
设Σ0是M的子集的一个集合,如果M中每一个点都有一个邻域,它仅与Σ0中有限多个成员相交,则称子集簇Σ0是局部有限的。
设Σ1、Σ2是M的两个开覆盖,如果对于Σ2中任意一个成员V,必能在Σ1中找到一个成员U,使得,则称Σ2是开覆盖Σ1的加细。
引理1.1[11](单位分解定理)设M是满足第二可数公理的n维光滑流形,是M的任意一个开覆盖,则Σ必有一个可数的、局部有限的加细开覆盖,以及定义在M上的一簇光滑函数,使得是包含在Vi内的紧致子集,并且。
光滑函数簇称为从属于Σ的单位分解,也称为定义在M中满足单位分解的光滑函数簇。由于,且是局部有限的,所以每一点p∈M必有一个邻域W,使紧致,因而W只与有限多个邻域Vi相交,换言之,只有有限多个函数fi在点p不为零,故只是有限多项的和。
2 线性空间中光滑函数的单位分解性
本节构造了线性空间X中拓扑的一个可数拓扑基,显示了X是满足第二可数公理的光滑流形,利用单位分解定理引理1.1建立了一簇光滑函数,函数值介于0到1之间且全部求和恒等于1的光滑函数簇,每个函数的支撑集是紧致的,如定理2.1所示。
首先,对于实数域R上n维线性空间X给定一组基底{η1,η2,…,ηn},其中,η1,η2,…,ηn∈X,对于任意x∈X,可唯一表示为
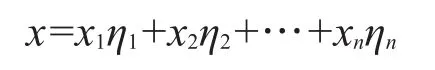
其中x1,x2,…,xn∈R。故只要在X中给定一组基底,对于X中任意一个向量x与唯一的n元实数组(x1,x2,…,xn)一一对应,即是X同构于欧氏空间R2,记为全文若无特别说明,总认为n维线性空间X给定一组基底为{η1,η2,…,ηn}。
规定X中的零向量,不失一般性,对于任意x∈X,对应的唯一的n元实数组表示为(x1,x2,…,xn),故零向量O对应的唯一的n元实数组表示为(0,0,…,0)。可以在n维线性空间X中定义一个度量映射

即对于任意x,y∈X,令

容易验证p是X的一个度量。事实上,对于任意x,y,z∈X,有
(1)p(x,y)≥0,当且仅当x=y时取等号。当x=y时,则有xi=yi,i=1,2,…,n,则(xi-yi)2>0,所以;当x≠y时,至少存在一个xi≠yi,i∈{1,2,…,n},使得(xi-yi)2>0,故
(2)p(x,y)=p(y,x)。这是因为

(3)p(x,z)≤p(x,y)+p(y,z)对于任意(u1,u2,…,un)(v1,v2,…,vn)∈Rn由Schwarz不等式得进而有

变形为
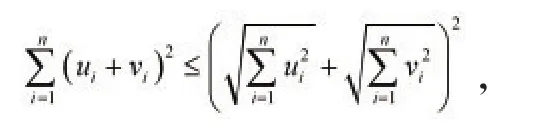
等价于

令ui=xi-yi和vi=yi-zi,所以,

即,p(x,z)≤p(x,y)+p(y,z)。因此,X是以p为度量的一个度量空间。
在n维线性空间X中,对于任意x∈X,规定以点x为中心,半径为a的n-1维超球面定义为:

和以点x为中心,半径为a的n维开球体定义为:
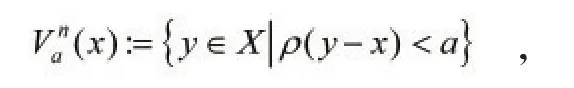
其中a∈R+。根据超球面和开球体的定义可得下列关系式:

根据度量空间X球形领域的定义可知,开球体是x的一个球形邻域,且在度量空间中每一个球形邻域都是开集[12],于是有下列引理2.1。
引理2.1对于任意x∈X,a∈R+,开球体

是X中的开集。
对于任意x,y∈X,且x≠y,则p(x,y)>0。取有。因为在X中的开球体是开集,故分别是点x,y的邻域,所以X是一个Hausdorff空间,由得,X是一个n维拓扑流形。取U=X,对于任意x∈U,定义映射φ∶U→Rn,即

下面给出一个在实数域R上n维线性空间X中建立的单位分解定理,指出存在一簇光滑函数,满足,如定理2.1所示。
定理2.1在n维线性空间X中,设是X的任意一个开覆盖,则Σ必有一个可数的、局部有限的加细开覆盖,以及定义在X上的一簇光滑函数
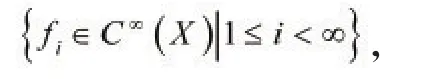
使得 0≤fi≤1,Supp fi是包含在Vi内的紧致子集,并且
证明(1)证明线性空间X是满足第二可数公理的n维光滑流形。
已知(X,p)是一个度量空间,设Γp为由X中的所有开集构成的集簇,根据度量空间的开集的性质和拓扑的定义,得Γp是X的一个拓扑,故(X,Γ)是一个拓扑空间。
现在考虑用X中部分开球体表示的集簇Φ,表示为
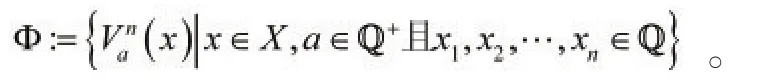
首先,验证Φ是X中的拓扑Γp的一个基[5]。事实上,对于X中的每一个点x和点x的每一个邻域U,则存在一个球形邻域B(x,ε),使得其中ε>0,任取y∈B(x,ε),使得,即是
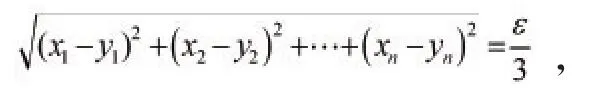
其中,xi,yi∈R,i=1,2,…,n。根据有理数在实数中是稠密的,即在任意两实数之间必存在有理数,于是存在ui∈Q,使得xi<ui<yi或者yi<ui<xi,由此有

设u=u1β1+u2β2+…+unβn,则u∈X,于是有又根据有理数的性质可得,存在q∈Q,满足使得p(x,u)<q,故x∈B(u,q),即是x属于以点u为中心,以点q为半径的球形邻域B(u,q)。
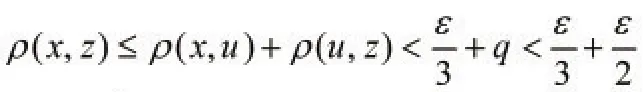
易知,点u的球形邻域B(u,q)就是本文定义的开球体,即(u,q)∈Φ,可表示为。于是有,因此集簇Φ是拓扑空间X中的拓扑Γp的一个基。
然后,又根据有理数集Q和正有理数集Q+都是一可数集合,可知

也是一可数集合[12]。所以,集簇Φ是拓扑空间中的拓扑Γp的一个可数基,即是拓扑空间X满足第二可数公理。
已知线性空间X是一个n维光滑流形,因此,线性空间X是满足第二可数公理的n维光滑流形。
(2)证明在线性空间X中存在一簇光滑函数,且求和恒等于1。
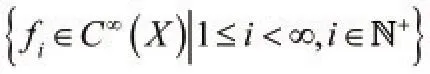
使得0≤fi≤1,Supp fi是包含在Vi内的紧致子集,并且
定理证毕。
3 凸体中函数的单位分解性
对于一个实数域R上n维线性空间X的任意紧子集A,对于任意x∈A,点x的球形邻域组成了A的一个开覆盖,又由A是紧的,则存在有限个球形邻域组成的开覆盖,设为B(xi,εi),i=1,2,…,s,其中s∈N+。由定理2.1可知,对于每一个B(xi,εi),都与局部有限的开覆盖∑0中有限个成员相交,故存在有限个定义在X上的上节定理2.1中所描述的光滑函数,使得这些光滑函数在B(xi,εi)上函数值求和等于1。故存在有限个定义在紧子集A上的光滑函数,设为g1,g2,…,gs∈C∞(A),满足和0 ≤gi≤1,其中s∈N+。
对于有限个满足单位分解的函数,提出一个问题,如问题1所示。
问题1:对于线性空间X中的紧子集A,对于任意n∈N+,是否存在n个定义在A上的连续函数g1,g2,…,gn∈C(A),满足且对任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2,…,n。
目前,当n=2时,可以构造两个连续函数,使问题1成立。事实上,设h是定义在紧子集A上的任意有界连续函数,令构造函数

显然,g1,g2∈C(A),满足g1+g2≡1,0≤g1,g2≤1 且对于任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2。这里,符号A表示集合A的闭包。
但对于n=3,这种构造方法构造的三个连续函数,不一定使问题1成立。事实上,对于定义在紧子集A上的任意有界函数h1,h2,令,其中i=1,2。构造函数

显然,g1∈C(A),满足0≤gi≤1且对于任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2。设g2=1-g1-g2,显然g1+g2+g3≡1,但很难确定,对于任意a∈(0,1),存在xi∈A,使得g3(x)=a。这是因为取,存在函数

满足g1(x)+g2(x)+g3(x)≡1,显然g1(x),g2(x)在上的值域为(0,1),但

线性空间X中凸体的相关定义如下:
现在考虑2维线性空间X,由于X与平面R2同构,故只需证明在平面R2存在3个连续函数使问题1成立。为了便于叙述,取平面R2的一组基底为{η1,η2},其中η1=(1,0),η2=(0,1)。在平面R2上,对于任意,a∈R2,是以a为圆心,以a为半径的开圆面。是以a为圆心,以a为半径的圆,不失一般性,为了全文符号使用的统一,仍使用此符号表示平面R2中的开圆面和圆。
对于平面R2,通过构造一种特殊的开覆盖,应用线性空间X的单位分解定理2.1,证明了在一个开凸体A上存在3个连续函数g1,g2,gs∈C(A),满足g1+g2+g3≡1,0≤gi≤1 且对任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2,3。这样就确定了n=3时,对于平面R2的开凸体A,问题1成立。然后,利用平面R2中的任意两开凸体A,B同胚,证明了对于任意开凸体A,问题1成立。
引理3.1[12]对于任意集合若A,B是开凸体,则A与B同胚。
易知,在开凸体A与B之间,存在的同胚映射φ(x)是一个光滑映射。
定理3.1对于平面R2上的任意开凸体A,存在定义在A上的3个连续函数g1,g2,g3∈C(A),满足0≤gi≤1 且对任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2,3。
证明(1)在平面R2上构造一个开凸体intΩ满足定理结论。
现在构造平面R2的一种特殊的可数开覆盖,如图3所示,表示为规定符号intS表示集合的内部,设△ABC是一个边长为1等边三角形,△ABC的中心为点O,则
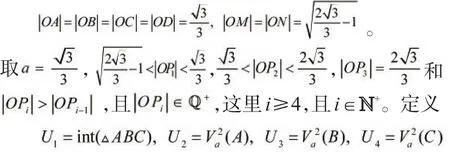
和当i≥5,且i∈N+时,。易知,,并且对于任意的正整数i,Ui都是开集。事实上,(a)显然,U1,U2,U3和U4是开集。(b)当i≥5,且i∈N+时,任取则,取,于是有球形邻域,故由开集定义可得,Ui是开集。

图3 平面R2的一个可数开覆盖
使得 0≤fi≤1,Supp fi是包含在Vi内的紧致子集,并且


显然,f1在intΩ上也是光滑函数,且0≤f1(intΩ≤1。现在验证对任意a∈(0,1),存在x∈A,使得f1(x)=a事实上,f1在intΩ上的函数值不恒等于0或1。根据f1在intΩ上是光滑函数,知f1在intΩ上也是连续函数,若f1(intΩ)≡0时,则对任意x∈intΩ,有,这与f1(O)=1相矛盾;若f1(intΩ)≡1时,在直线MN任取一点W,则f1(W)≡0,又因为,对任意x∈intΩ,有,这与f1(W)=0相矛盾。于是,对任意a∈(0,1),必存在x∈A,使得f1(x)=a,否则,f1在intΩ上不是连续函数。
同理,f3,f4在 intΩ上也是光滑函数,0≤f3(int Ω),f4(intΩ)≤1且对任意a∈(0,1),存在α,β∈A,使得f3(α)=f4(β)=a。
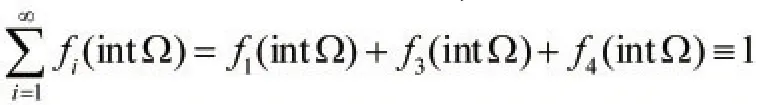
在intΩ上定义新函数

0≤gi≤1,且对任意a∈(0,1),存在xi∈A,使得g1(xi)=a,其中i=1,2,3。
由开凸体的定义得,intΩ是一个开凸体。综上所述,对于开凸体intΩ,定理结论成立。
(2)证明在平面R2上任意开凸体A满足定理结论。
由引理3.1可得,在开凸体A与intΩ同胚,即存在同胚映射y=φ(x)∶A→intΩ,则映射φ是一个连续映射.在开凸体A上定义函数

在开凸体A上定义新函数gi∈Gi,i=1,2,3。综上所述,存在定义在开凸体A上的连续函数g1,g2,g3∈C(A),满足,0≤gi≤1 且对任意a∈(0,1),存在xi∈A,使得gi(xi)=a,其中i=1,2,3。
定理证毕。

