自由度并联腿机构运动学分析

王晓芸 李 磊 崔 培

（石家庄铁路职业技术学院 河北石家庄 050041）

1 引言

近年来，少自由度并联机构具有结构简单紧凑、承载能力大、累计误差小、造价低、运动惯性力小等优点，逐渐成为国际上机器人技术中研究的新热点，在工业设计制造生产及其相关领域内具都有非常广阔的应用前景。但是，由于大多数少自由度并联机构中存在过约束和自由度耦合等现象，所以这类并联机构的运动学分析较复杂，运动规律难以直观判别[1]。因此，提出了一种新型的2自由度并联腿机构，即 2-UPS+U 并联腿机构，该机构结构简单，支链无耦合，刚度大，承载能力高。

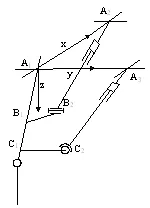
图1 机构简图

2 并联腿机构模型建立

（2-UPS+U）并联腿机构，由三条支链构成，分别是一条U支链和两条UPS支链。其中，U支链为动杆，具有2个转动自由度，它上部通过虎克铰链与机架相连接；UPS支链上部通过虎克铰铰链与机架连接，下部通过球副与U支链的动杆相连接；与机架连接的3个虎克铰链中心布置在等腰直角三角形的三个顶点处，并且保证U支链的虎克铰链中心位于该三角形的直角顶点处。该机构结构简单，无耦合，可以将2-UPS分支的驱动器放置在机架上，减小整个并联腿机构运动部分的质量。图1是并联腿的机构简图。建立固结在三角形机架上的固定坐标系O0-XYZ，其原点在直角顶点处A1，其X轴平行于机架的直角边A1A2方向，Z轴垂直于机架向下，Y轴的方向由右手法则确定。分别在3个虎克铰链中心A1、A2，A3建立动坐标系{1}、{2}、{3}。

3 并联腿机构运动学分析

3.1 机构自由度求解

在（2-UPS+U）并联腿机构中，U支链的反螺旋[2]可以表示为：

并联腿机构中UPS支链的反螺旋可以表示为：

由上述反螺旋公式可以看出，反约束力$14r和$22r对限制该并联腿机构沿Z轴移动所起的作用是相同的，反约束力$12r和$21r对限制该并联腿机构沿X轴所起的作用是相同，因此，该并联腿机构中存在两个冗余的虚约束。

考虑了冗余约束的 Grübler- Kutzbach公式[3]为：

式（3）中d为并联腿机构的阶数，λ为并联腿机构的公共约束数目，则d=6-λ；n为机构的构件数；g为机构的运动副数目；∑fi为第i个运动副的自由度；Ω为虚约束的数目；q为机构的局部自由度[3]。

由上述并联腿机构的分析可知：λ=0；d=6；n=6；g=8；∑fi=13；Ω=2；q=0，将其代入可得该并联腿机构的自由度为：

3.2 位置反解

机构的位置反解就是机构末端的位置和姿态角，求解机构中各个驱动副的输入。对该并联腿机构而言，就是已知该并联腿末端点O1相对固定坐标系的位置P与姿态角（α，β，γ），求解并联腿机构中UPS支链中移动副的两个输入参数l2，l3[4]。

采用XYX欧拉角，设并联腿机构的运动坐标系{1}相对于固定坐标系{0}的位姿变换矩阵位，则为：

式中

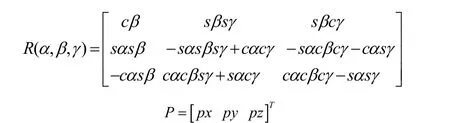
其中，cα=cosα，sα=sinα。

给定机器人并联腿机构动杆末端相对于固定坐标系的位姿矩阵为：

运动坐标系中的点在固定坐标系中的坐标可由以下公式求得可得：

又因坐标系{1}相对于坐标系{0}的姿态是通过旋转实现，由此可以构造得到：R1⊥R2，R2⊥l1，R2∥o， l1∥a，其中R1是U支链的第一个旋转轴，R2是U支链的第二个旋转轴，l1为U支链的方向向量，o为坐标系{1}的Y向量，a为坐标系{1}的Z向量。

由以上关系可得：sβsγ=0，γ=0，

化简得：

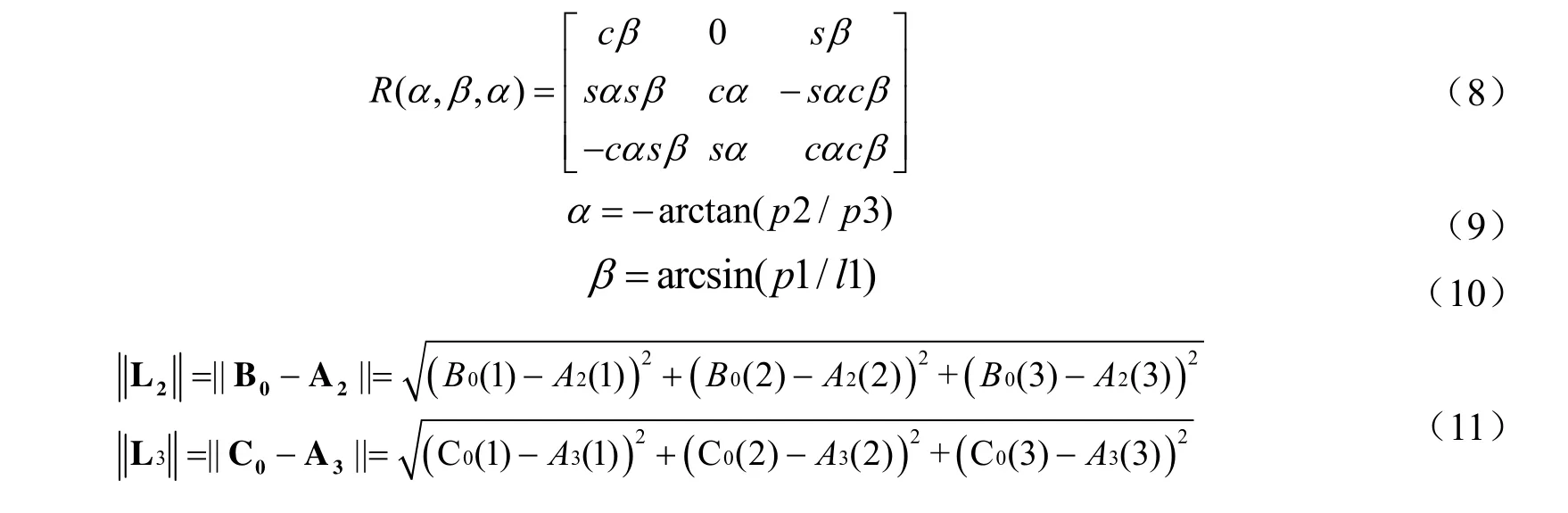
故支链移动副输入为：

因此，若给出机器人并联腿机构动杆末端点的位置坐标和姿态角，即可求出并联腿机构各移动副的输入。

3.3 位置正解

给定机构的各输入参数求解动平台的位姿参数是并联机构的运动学位置正解问题。采用数值法求解该机构运动学正解，就是已知U支链移动副输入l2，l3，求解动杆末端点O1相对固定坐标系，的位置P与姿态角（α，β，γ）。运动坐标系{1}相对于固定坐标系{0}的位姿变换矩阵位为：

由运动学反解求解得到的关系可求得：

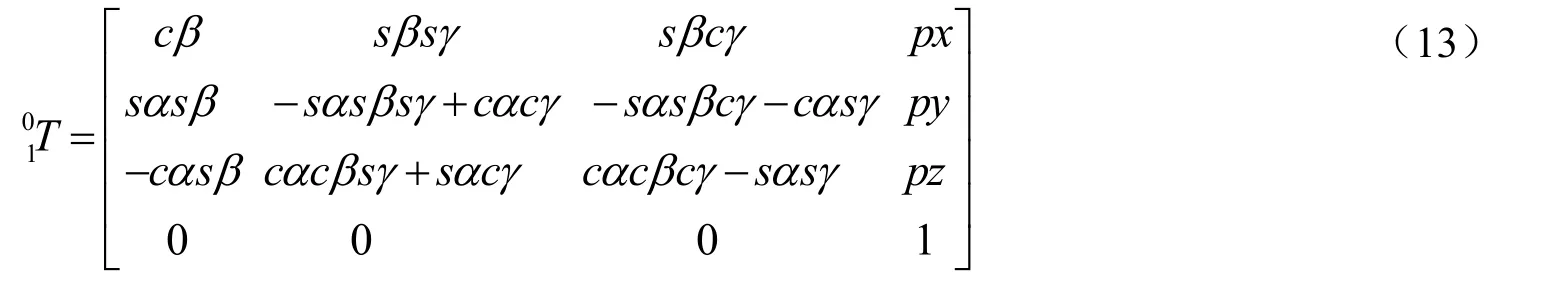
以上五个式子中，含有px，py，pz，α，β五个未知数，用最小二乘法可求其解，其目标函数为：

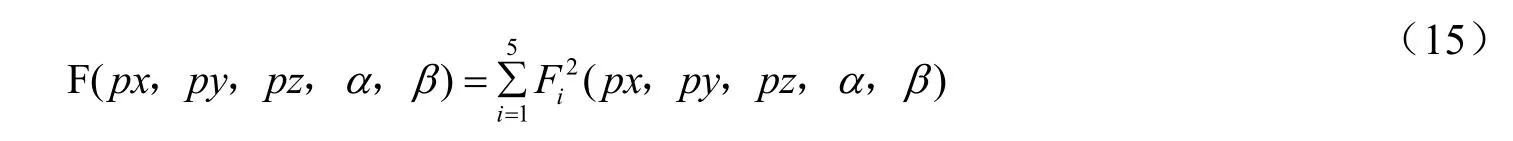
即可求得其并联腿机构末端O1的位置坐标和姿态角。

4 工作空间

4.1 工作空间分析

由（2-UPS+U）并联腿机构的结构特点可知：工作空间主要由两条UPS支链中移动副的杆长、三条支链的干涉情况、以及并联腿机构中虎克铰链与球铰链及转动副的转角限制共同确定[5][6]。

（1）并联腿机构两个UPS支链中连接杆具有长度限制，故各两条支链的长度变化范围为：

式（16）中，limin为UPS支链的最小长度；limax为UPS支链的最大长度。

（2）(2-UPS+U)并联腿机构中的球铰链能够实现的转角范围存在一定的限制。q3为球铰链座与动杆固联的单位法向量，l3为UPS支链的方向向量，球铰链的结构转角η3为：

若η3max为球铰链所能达到的最大转角，则球铰链转角的转动条件为：

（3）并联腿机构中的虎克铰链转动时在一个倒三角锥内任意摆动，ψmax为倒三角锥的锥顶角，由虎克铰链结构限制。因此，支链向量与倒三角锥轴线之间的夹角为ψi应满足：

（4）(2-UPS+U)并联腿机构各杆件选用均匀截面圆杆，因此，相邻支链的杆件之间可能发生干涉，假定各杆件之间的最短距离为dij(i，j=1，2，3)且i ≠ j，d为杆件直径，则杆件需满足：

4.2 工作空间求解

并联腿机构的工作空间是指并联腿机构末端所有可以到达的点的集台，即为O1点。采用数值法对该机构进行定姿态工作空间分析，就是给并联腿机构末端的姿态方位角(α，β，γ)，求解满足结构约束的条件下参考点O1点位置坐标的集合，即用极坐标搜索法逐个搜索参考点能达到的所有空间点[7]。机构参数如表1所示。

表1 机构参数

当姿态角α=β=γ=0时，其工作空间边界三维实体如图2所示：由图可见，该机器人腿部结构的工作空间较大、连续性好、空间对称性好。

5 结语

提出了一种新型的2自由度（2-UPS+U）并联腿机构模型。该机构结构简单，支链无耦合，刚度大，承载能力高，可用作机器人的腿部机构。利用螺旋理论对该并联腿机构进行了运动学分析，计算出其自由度，推导出了该并联腿机构的位置反解方程和位置正解方程，并进行了工作空间分析，利用MatLab软件绘制出了并联腿机构末端的工作空间三维图，为后期并联腿机构及整个步行机器人的的运动规划以及控制奠定了理论基础。

图2 并联腿机构工作空间